模块化决策森林的区块链交易欺诈检测模型

田红鹏，韦 甜

西安科技大学 计算机科学与技术学院，西安 710600

区块链技术的快速发展引起了政府部门、金融机构、科技企业和资本市场的广泛关注，相应的虚拟货币金融欺诈现象也层出不穷[1]，主要包括账户资金被盗[2]、一币多用[3]、可追溯性差[4]等。由于虚拟货币的匿名性和隐私性，执法部门在追踪可疑交易时遇到额外障碍[5-6]。神经网络及机器学习在复杂多变量系统的处理能力[7]和预测[8]等领域取得了良好的效果，因而利用神经网络及机器学习技术检测金融欺诈是未来的趋势。

传统区块链欺诈检测方法通过人工规则和静态阈值来标记可疑交易地址[9]，但由于欺诈者不断调整欺诈规则，混淆静态规则从而绕过审查，因此人工静态规则存在一定的局限性[10]。喻文强等人[11]通过机器学习的方法来检测匿名化实体欺诈行为和庞氏骗局等问题。Weber 等人[12]发布由20 万组比特币交易样本所构成的数据集，并评估多种有监督机器学习模型，实验结果表明机器学习模型具有收敛速度快优点。Monamo等人[13]研究裁剪k-均值聚类在无监督犯罪检测中的准确率。林伟宁等人[14]提出基于PCA 和随机森林分类的入侵检测算法，提高了欺诈检测的准确性。虽然机器学习收敛速度很快，但由于虚拟货币交易系统复杂、欺诈手段多变影响了机器学习模型对欺诈网络的有效判断，导致假阳性过高，检测准确率较低等问题。神经网络具有自学习能力，能够充分提取时间和空间的有效信息，所以在欺诈检测领域具有发展前景。Kurshan等人[15]提出使用图神经网络学习空间交易拓扑结构的有效信息，提高金融欺诈检测的准确率。Qian 等人[16]结合比特币网络交易节点的自身特征和邻域特征，提出无监督特征融合异常交易检测的方法，提高了异常交易的检测能力。张昊等人[17]对比现有的基于深度学习的入侵检测模型，指出在数据集时效、普适性、模型等方面依然存在准确和实时性较低的问题。文献[18]模拟人脑处理信息方式，设计了多层自适应模块化神经网络，以自适应确定模块及神经元的数量，且学习精度高泛化能力强。相对于机器学习，虽然神经网络能够得到更高的准确率，但由于区块链交易去中心化的特性，缺乏大量非法交易数据，导致上述依赖大量学习样本的神经网络难以有效检测区块链的欺诈行为。

针对数据特征多的问题，本文采用改进的稀疏去噪自编码器（sparse denoising autoencoder，DAE）将高维空间的输入数据映射到低维空间，以实现数据降维。其次对于交易复杂的问题，本文根据欺诈交易节点呈现出一定关联的事实，提出一种模块化决策森林（modular decision forest，MDF）算法，采用一种数据概率密度峰值以确定聚类中心个数[19]，再结合模糊C均值（fuzzy Cmeans，FCM）聚类算法将数据分解为多组子数据。每个子数据将会采用多个决策树模型进行学习，边缘分界明确的样本将会在一组决策树中学习，而对于模糊边界样本，则会由多个不同类别的决策树集成学习。最后，本文分别对Elliptic 和Ethereum 欺诈交易数据集分类，验证所提模型的性能。

1 基于模块化决策森林的欺诈检测模型

基于MDF 的交易欺诈检测模型包括数据集预处理、特征提取网络和模块化决策森林分类三大部分。首先预处理虚拟货币交易数据。然后训练特征提取网络，训练过程为改进的DAE 降低数据维度并提取数据特征。在建立特征库后，使用快速聚类算法结合FCM 将数据分成不同的子模块，然后由不同的分类器构建分类集，最后通过投票得出分类结果。交易欺诈检测流程如图1所示。

图1 交易欺诈检测结构示意图Fig.1 General diagram of transaction fraud detection process

1.1 改进DAE数据特征处理

稀疏去噪自编码网络的出现是在标准自编码网络的基础上做了进一步的改进，其基本原理[20]：DAE 与传统的编码器不同之处在于去噪自编码器的隐层特征表示是对输入数据“损坏”。为了更好地显示数据的原始特征，因此加入KL（Kullback Leibler）散度[21]以此来优化稀疏编码过程。如图2表示去噪散度特征提取网络，其结构包括噪声输入、稀疏散度计算、编码器和解码器。去噪自编码器就是向输入数据引入高斯噪声，通过学习去除高斯噪声以尽可能获得原始输入，使提取到的特征更能反映原始输入的特点，减少噪声干扰。去噪稀疏自编码器的训练主要流程分为以下两个过程：

图2 去噪散度特征提取网络Fig.2 Denoising dispersion feature extraction network

（1）加入噪声

首先对原始信号x输入高斯噪声，得到受损信息x͂，编码后映射到隐含层，最后经过解码函数将处理后的信息映射到输出层获得重构信号x̂。公式如下：

对于给定的n个训练样本x={x1,x2,…,xn}的每个样本xi，xi=[x1,x2,…,xn]T，编码器将输入向量x经过Sigmoid激活函数转换为隐藏层编码表示h={h1,h2,…,hn}，其中表达式为：

其中，x和h分别是D维和d维向量；W(1)为d×D维的权重矩阵；b(1)为d维偏置向量；Sf是激活函数。隐藏层编码向量h被解码器转换为重构向量̂，̂=

其中，̂是D维向量；W(2)为D×d维的权重矩阵；b(2)为D维偏置向量。

（2）高度还原真实特征

去噪自编码器的训练目标是通过不断优化模型参数θ={w(1),b(1),w(2),b(2)}以使得重构误差最小。当x为实数时，选择均方误差（MSE）用作标准的自动编码器损失函数较为合理。

数据特征对欺诈检测结果至关重要。为了更好地将表达数据特征，本文引入代价函数增加KL 散度以此来优化稀疏编码过程。通过二者的结合，可拥有接近先验分布（自然统计概率）并可以描述输入特征。

KL散度计算公式为：

其中，DKL为度量两个概率分布函数之间的“距离”，p(x)为期望数据分布，q(x)为初始数据特征分布。以上两种分布的匹配程度与KL散度输出值呈正相关。代价函数通过重构误差结合期望分布与样本分布KL散度计算得来，公式为：

式中，为第i个训练样本：xi为第i个解码输出：n为特征样本总数；β为权值系数；p为常数，用于代表期望的稀疏分布；qj表示编码器输出值中第j个特征的平均激活度，训练阶段通过反向传播迭代更新权值矩阵。

自编码器网络中的输入集加入不同的噪声且散度处理，然后通过学习去除噪声可以获得没有被噪声污染的输入，这样编码器能更好地学习特征表达。

1.2 数据集模块化

虚拟货币以及金融交易往往存在维度高、数据大的特征，而大数据的分类算法存在计算时间长，效率低等问题。数据需要通过聚类划分训练样本，故本文采用基于数据点概率密度峰值的快速聚类算法用来确定模块化随机森林中子模块的数量，其中ρi表示数据点i的局部概率密度，δi表示数据点i与其他具有更高局部密度数据点之间的最小距离。S={(xk,yk)|xk∈R,yk∈R,k=1,2,…,N}为训练样本集，对于S中的任意一个训练样本xi，ρi和δi的定义为：

其中，dij=dist(xi,xj)表示样本xi和xj之间的欧氏距离，dc>0 表示截断距离。本文根据式（10），可以确定聚类中心的个数，显然γ值越大，越有可能是聚类中心。因此，只需降序排列，就可以生成数据点作为聚类中心。

设上述聚类算法共构建k个聚类中心，c={c1,c2,…,ck}，通过所构建聚类中心将训练样本集划分k组训练样本。

确定子模块的数量后，本文提出一种数据点概率密度峰值结合FCM 算法，用来确定模块化神经网络中子模块的聚类集合。该算法的核心一是保证同一簇对象的相似度最大；二是增加模糊集合的概念，使得簇的隶属度为[0，1]。该算法是一个迭代过程，分别使用两个参数ci和dij描述模糊组的聚类中心和第i个聚类中心与第j个数据点间的欧式距离。模糊集群的输入和输出变量都有一个隶属函数，根据式（11）计算并更新隶属度：

其中，m(m>1)是模糊分区矩阵指数，用于控制模糊重叠的程度。模糊重叠是指聚类之间边界的模糊程度，即在多个聚类中具有重要成员身份的数据点数。xi是第i个数据点；cj是第j个聚类的中心；μij是xi在第j个集群中的隶属度函数，对于给定的数据点xi，所有聚类的集群隶属度之和为1。具体算法描述如算法1，展示数据模块化算法流程。

算法1模块化聚类算法

输入：训练数据集S

输出：聚类矩阵U

1.初始化：随机初始化对象的各个属性值，并计算样本xi和xj之间的欧氏距离dij；

2.通过公式（8）计算ρi降序排列，并保存原始索引顺序至矩阵P；

3.fori=1:ndo

4.δ(P(i))=max(dij)；

5.forj=1:k-1 do

6.ifd(P(i),P(j))<δ(P(i)) then

7.δ(P(i))=d(P(i),P(j))；

8.end if

9.end for

10.end for

11.根据公式（10）确定聚类中心以及聚类个数；

12.fori=1,2,…,ndo

13.根据公式(11)计算隶属度，并根据隶属度构建聚类矩阵U；

14.end for

综上所述，上述算法可以分出N个聚类中心以及针对N个中心建立模糊集，然后可以划分出N个功能模块。在存在大量特征的数据集中，该方法使得每个聚类集群特征更为高效、分类性能更优。

1.3 模块化决策森林

模块化决策森林是一种集成学习方法，其通过聚集多个“弱学习器”，形成一个“强学习器”，作用是将复杂问题分解成多个相对简单的子问题由不同子模块处理，最后将学习结果集成以完成对整个复杂问题的求解。本文首先利用改进DAE 降低特征维度，然后采用聚类方法划分训练样本，最终采用多个决策树进行学习。

如图3所示为数据聚类结果，其中红色圆圈表示属性a，蓝色圆圈表示属性b，红色×表示属性a的聚类中心，蓝色×表示属性b的聚类中心，黑色带圆圈的×表示边界分类不清晰数据。随着模糊分区矩阵指数M的增长，存在部分数据集模糊重叠的现象。而重叠部分往往是决策树难以划分的区域，导致分类结果准确率下降。为了解决重叠数据聚类不清晰的情况，本文采用MDF分别学习划分后的整体数据和边界数据，以达到强化重叠数据学习的效果。且由于聚类过程中可以归纳数据特征，降低决策树处理的复杂程度，从而使决策结果更易于理解。模块化决策森林模型如图4所示。

图3 数据聚类结果Fig.3 Results of data clustering

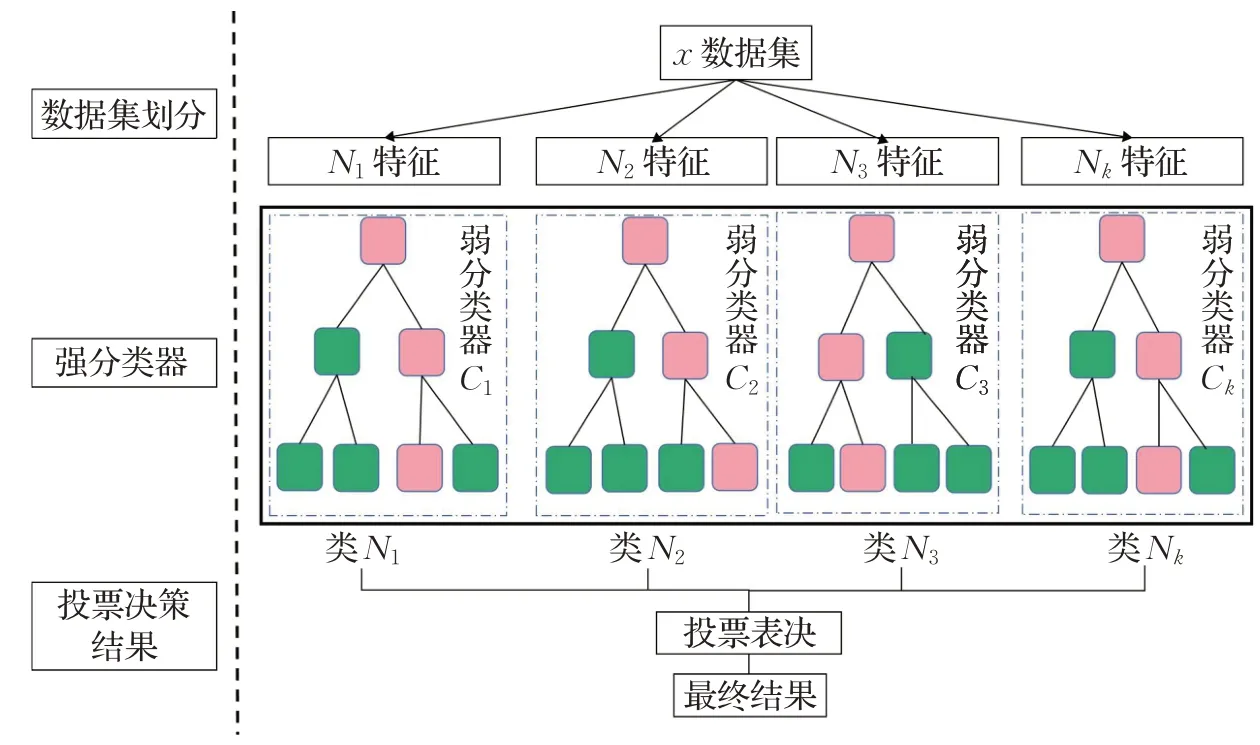
图4 模块化决策森林Fig.4 Modular decision forest

MDF 包含强分类器和弱分类器，分类结果由多个弱分类器与强分类器集成学习得到。每个聚类矩阵至少拥有一个强分类器，而弱分类器则根据学习策略来自适应添加。分类器最优结果采用信息增益与增益率来共同选择特征集中的最优划分属性，如式（12）~（15）所示。首先根据式（13）从划分属性中寻找信息增益高于平均值的属性，再根据式（14）从中选择最高增益率的属性。决策树算法如算法2所示。

算法2构建决策树

输入：训练集S；特征集N

输出：以node为根节点的决策树

1.生成节点node；

2.if当前节点样本集中样本属于同一类别kthen

3.node标记为k类叶节点；return

4.end if

5.if 特征集合N=∅ OR 所有样本的特征相同无法划分then；return

6.end if

7.根据式（13）和（14）选择特征集中的最优化分属性a；

8.for生成a对应的值a* do

9.生成node节点的分支；并获得a*的样本子集；

10.if样本子集为空then

11.将分支记为叶节点，这类标记为样本最多的类；return

12.else

13.以此节点作为分支节点；

14.end if

15.end for

信息熵定义：

计算信息增益：

计算增益率：

其中，S为样本集合，Pk为S中第k类样本所占比例；Sv为第v个节点在属性a上的取值为av的样本集合；IV(a)是属性a的固有值，属性a的种类越多，则IV(a)越大，增益率变小。

模块化数据集经过初步分割得到训练样本，但对于训练样本数量大、样本种类多的问题，分配给不同决策树仍然存在复杂度高的问题。为了进一步提升模块化决策树（modular decision tree，MDT）的学习性能，对基于算法1建立的模块化数据集中部分模块进一步划分，划分策略及模块化决策森林如算法3所示。

算法3再划分策略及模块化决策森林

输入：训练集S；特征集N

输出：分类结果

1.根据算法1得k个聚类中心与聚类矩阵U

2.case1：if所包含的训练样本类别数>Q，then

3.采用算法1进一步划分，设子聚类中心为km个；return

4.case2：if单个模块训练样本个数>N/k，then

5.采用算法1进一步划分，设子聚类中心为km个；

6.kall=k+km；//计算总的聚类中心个数

7.fori≤kalldo

8.对每一组聚类矩阵采用算法2进行学习；

9.if 最大隶属度<0.6 then

/*认为该点属于模糊重叠区*/

10.对每一组聚类矩阵的模糊重叠区域采用算法2 进行学习；

11.同一学习样本采用多组决策树学习的，通过式（16）集成学习；

12.i++；

13.end if

14.end for

经过上述算法多次划分训练样本，可将数据集先划分出K个数据模块，每个需划分的数据模块中又可划分出数量不等的子模块。以此降低每个决策树划分的难度，提高整体分类的性能。与随机森林不同的是，本文所提模块化决策森林，采用聚类算法与划分策略来确定决策树数量，且针对学习不同的数据特征，实现了“按需分配”“分而治之”的思想。

通过MDF 已实现各模块的分类结果，在众多分类任务中，学习器C需要从类别集合{N1,N2,…,Nn}中预测一个标记，本文使用加权投票法（weighted voting）实现结果集成，如公式（16）：

其中，H(x)是最终的预测输出结果，hij(x)是hi在类别标记cj上的输出；wi是hi的权重，通常

2 实验与分析

实验设置：操作系统为Windows10，CPU 主频为2.5 GHz，内存8 GB，仿真软件Matlab2021a。其中实验所用数据集为UCⅠ真实数据集和kaggle数据集，数据集Optdigits 有7 500 个训练样本和3 500 个测试样本。数据集Ethereum 和数据集Elliptic，训练集和测试集拆分的比例均为4∶1。

2.1 数据集

（1）为验证本文所提模块化决策森林的处理能力，选用数据集Optdigits，其中包含16个维度，7 500个训练样本和3 500个测试样本，属于10个类[22]。

（2）数据集Ethereum 是以太坊非法账户数据集，其中包括2 179 个非法账户和2 502 个合法账户。一共有42个特征，主要反映特定账户的交易细则[23]。

（3）数据集Elliptic 是比特币交易数据集，其包含交易关联网络、交易特征信息、时间信息，如表1所示。其中交易关联网络存在203 769 个交易节点和234 355 比特币交易流向流程。数据标签信息包含2%的Ⅰ类（非法），21%的ⅠⅠ类（合法）以及77%具有特征未标注的数据。每一个节点均包含166个关联特征，前94个表示基本交易信息，其中包括时间戳、输入输出数据、交易费、输出数量和合计值等。后72 个特征为聚合特征，是通过从中心节点向后或向前聚合而得，给出了包含信息数据（输入/输出数量、交易费等）的相邻事务的最大值、最小值、标准差和相关系数等。时间信息包括比特币网络中各个节点交易确认的瞬时时间，数据集将其划分为49个间隔为两周的时间步长，各个周期内的节点交易时间少于3小时。从交易数据来看，特定步长的每一个节点都具备相关性。

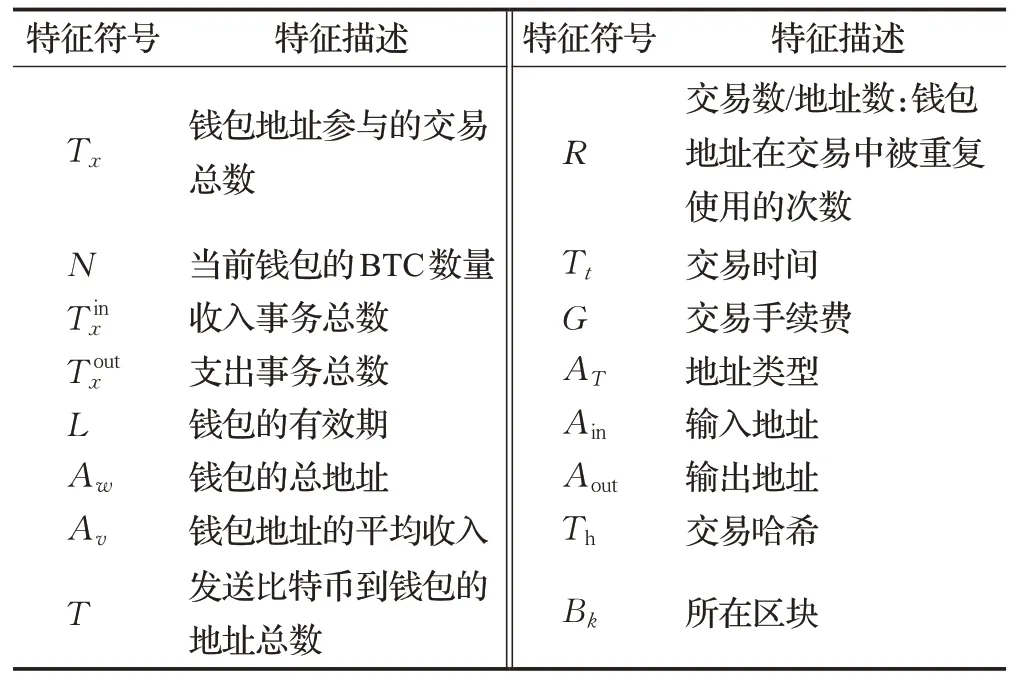
表1 部分交易特征描述Table 1 Description of transaction characteristics

选用Optdigits 数据集的原因在于维数高、类别多。该数据集没有缺失的特征值，在训练集和测试集中类别样本分布得非常平均规整，可用于验证数据划分、模糊边界处理的有效性。而Optdigits 数据相较于区块链数据，能使实验数据更容易理解模糊边界以及划分有效性。而区块链数据更多是Hash 值，从划分过程中难以理解模块化决策森林的划分效果。为了验证区块链欺诈应用的有效性，本文采用Ellipitic和Ethereum数据集，分别为非平衡和平衡数据集用于进一步检验模型的性能。而Elliptic 实验中可以看出，虽然随机森林能够达到类似的精确度，但召回率很低，容易对正常交易进行误判。

2.2 评价指标

虚拟货币的交易行为异常检测本质上是一个二分类问题，且由于异常交易行为的数量在实际中比正常行为的数量小得多，因此这里的异常检测是一个不平衡的二分类问题，故采用适合不平衡二分类的评价指标F1值。本文使用度量定义为：（1）真阳性（TP）正确识别欺诈交易；（2）假阳性（FP）错误识别正常交易为欺诈交易；（3）真阴性（TN）正确识别交易为正常；（4）假阴性（FN）将欺诈交易识别为正常交易。

精确度（precision）的定义为：欺诈交易中正确检测数量的占比。

召回率（recall）的定义为：数据集中正确检测的数量占比。

F1-score 为精度和召回率的调和平均值，作为有效性衍生度量。

宏平均值（MacroAVG）：宏平均是每一个类的性能指标的算术平均值，可以评估整个数据集的性能。

2.3 模块化决策森林有效性分析

为了检测MDF 的有效性和准确性，本文采用Optdigits数据集验证。此训练样本中存在10个类，如图5所示，有10个训练样本的局部概率密度与最小距离乘积的值γ最为突出。尤为重要的是，本文所提算法可以准确划分出数据集中的9个类别，表明该算法确实能够根据空间分布来识别聚类中心。由于类别1、2、5、7 本身局部概率密度与最小距离并不显著，将会导致传统算法对这些类别的划分难度提升，降低分类的准确率。

图5 确定聚类中心的结果Fig.5 Results of determining clustering centers

图6~8 均是通过混淆矩阵对所提模型性能的可视化表达，每一个小方格内的数值是不同类的预测结果，主要的评价参数是TP、FP、TN和FN。每一个决策树代表不同的模块化数据组。图6 为初步划分时模块化决策树的分类效果。聚类算法能够在训练决策树之前降低每个训练样本的复杂度，图6（a）、（c）所包含的类别均小于等于4，此时决策树往往具备不错的分类效果。但当划分类别大于4 时，会导致决策树分类错误率增大，如图6（b）、（d）、（f）所示。图6（e）虽然划分类别较多，但数据不存在聚类边界数据重叠现象，所以单个决策树仍然能够具备不错的预测效果。若数据划分类别多，存在过多边界重叠现象的问题，采用算法3中策略对模块数据集再划分。

图6 模块化划分数据集有效性验证结果Fig.6 Validation results of modular partition datasets validity

如图7 表示将模块数据4 进一步地划分，分别采用两个决策树学习，最后将学习结果集成，实验结果表明，单决策树4 中类别1 和2 的分类存在错误识别的问题，经过算法3 的再划分策略，得到的集成学习决策树4 的错误率为0，可以证明相对于初次划分能够进一步提升准确率，验证所提算法的有效性。

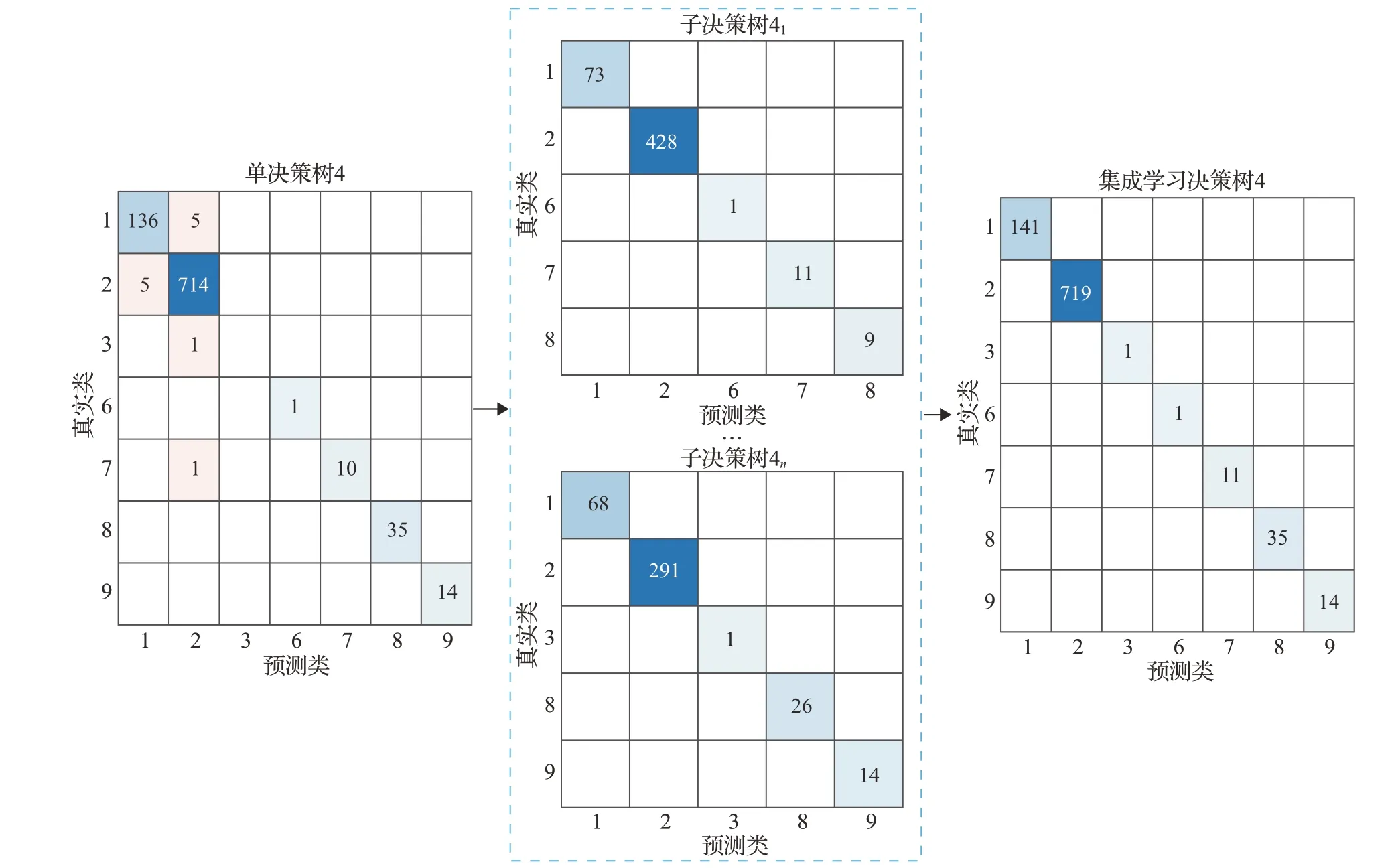
图7 子模块多次划分结果Fig.7 Multiple division results of sub modular

如图8 为传统决策树与模块化决策森林分类对比结果，其正确率明显提高。如表2 所示，模块化决策森林的精确度、召回率、F1-score 分别提高了6.37、6.59、6.52个百分点。

表2 传统决策树与模块化决策森林对比Table 2 Comparison of traditional decision tree and modular decision forest 单位：%

图8 传统决策树与模块化决策森林分类对比图Fig.8 Comparison diagram of traditional decision tree and modular decision forest classification

综上所述，模块化决策森林具有一定的有效性和准确性，该方法不仅保证两树之间的独立性，而且保证了边缘节点的分类准确性，进而可以提高模块化决策的准确性，提高决策树的泛化能力。

2.4 真实交易数据特征分析

采用真实交易数据验证改进的DAE，结果如图9所示。图9为抽取不同时间周期的交易拓扑图，图中红点表示非法交易，蓝点表示正常交易，红线表示具有关联的欺诈交易。第1~2 时间段的欺诈节点具备小范围分散特点，第11时间段的欺诈节点，出现大范围聚集且远点具备一定的关联性，时间段12则呈现小范围分散，但较远点具备一定关联性。上述特征说明在欺诈交易的节点附近会出现大概率的聚集性。而本文所提MDF则是针对不同的特点，选用不同的子模块，以提高特征筛选的泛化性。

图9 不同时间段的交易拓扑图Fig.9 Transaction topology view of different time periods

2.5 真实数据集准确率结果对比实验

为了检测出真实区块链交易中存在的可疑欺诈行为，以及测试DAE-MDF 对实际交易数据的处理能力。采用改进DAE 将数据集Ellipitic 和数据集Ethereum 分别降维至13维和30维，保证数据特征的原属性，而且对其进行归一化处理。本文所提的模块化决策森林欺诈检测模型（DAE-MDF）是在机器学习基础上的改进，因此通过常规随机森林（random forest，RF）算法作为消融实验，并与MLP（multi-layer perception）、XGB（eXtreme gradient boosting）、LGBM（light gradient boosting machine）模型对照，用于进一步验证本文所提模型的有效性，并在评估中采用RF 分类器作为基准进行比较。具体实验数据如表3和表4所示。

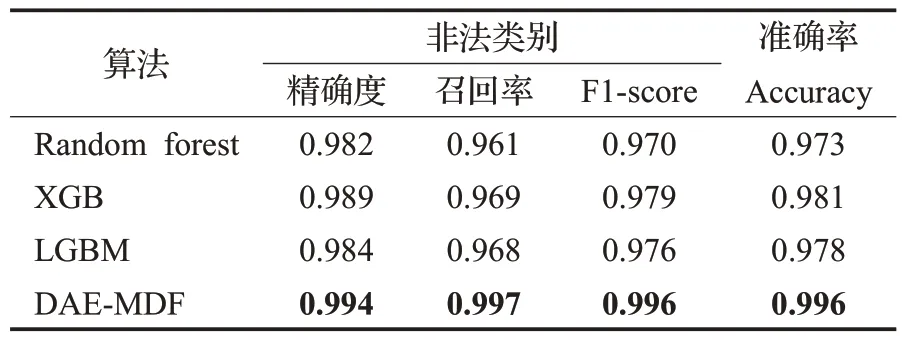
表3 Ethereum数据集模型对比Table 3 Comparison of models for Ethereum dataset

表4 Ellipitic数据集模型对比Table 4 Comparison of models for Ellipitic dataset

如表3体现各分类算法在不同指标下的性能，DAEMDF明显优于RF、XGB和LGBM分类器，相比较RF在精确度、召回率和F1-score方面分别增加1.2、3.6、2.6个百分点。由于Ellipitic数据集数据量大，特征表达不同，因此将数据集划分为所有特征（all feature，AF）、局部特征（local feature，LF）和图特征（node embedding，NE）[11]便于比较。具体情况如表4 所示，由表4 可以看出聚合信息具有更高的准确率，表明信息特征的重要性。相比较AF，本文DAE-MDF 方法在精确度、召回率和F1-score 方面分别提升7.0、26.2、17.5 个百分点，因此本文所提去噪稀疏自编码模块化决策森林表现出良好的性能。而GCN 使用逻辑回归作为最终的输出层，导致其预测结果并不理想。

综上所述，改进DAE-MDF是通过划分数据集构建针对不同特征的模块化决策树，从最终预测精度、召回率、F1-score均具有不错的性能，准确率方面也大幅提升。其原因在于MDF采用投票机制集成众多决策树的预测结果，每个决策树均通过使用数据集的子样本进行训练。

3 结束语

本文提出了一种基于模块化决策森林的区块链交易欺诈检测模型。该模型首先采用改进DAE提取数据特征，然后采用数据点概率密度峰值结合FCM算法，将大数据分解为多组数据，具有关联明确的样本会在一组决策树中学习，而对于分类不明确的边界样本则会有多个不同的决策树共同完成学习任务，最后通过集成学习得出最后分类结果。

为验证本文所提模型的有效性和准确性，首先选用数据集Optdigits 验证MDF 的有效性，为后续真实交易数据模块化处理提供理论基础。为了测试此模型在真实交易环节的稳定性和准确率，进而选用交易数据集Ellipitic，其主要特点是维度高，数据量大。从不同时段的交易拓扑图可以得出欺诈网络中存在一定关联的事实。最后通过三部分实验验证改进DAE 的稳定性、MDF 在准确率方面取得更好的性能和稳定性，准确率可达97.84%；第三部分在真实交易环境中对各类算法进行对比，本文所提改进的DAE-MDF 方法准确高达98.3%，说明此算法性能更优。