纤维加筋淤泥固化土的黏-弹-塑性本构模型

2023-10-10苏志明

科技和产业 2023年15期

苏志明

(天津市政工程设计研究总院有限公司, 天津 300051)

随着我国城市建设的不断发展,在市政、水利与海洋工程中常常产生大量的疏浚淤泥[1-3]。这些疏浚淤泥往往含水率、灵敏度高,工程性质差,若处置不当还可能产生二次污染[4]。与此同时,大量水利、道路、海岸工程中的土工填料仍需求旺盛,因而二疏浚淤泥的绿色化、资源化与工程化利用成为一个热门的研究话题。常见的一种淤泥固化方法是通过化学固化来提升其力学强度,其本质是利用固化剂与淤泥产生的水化反应产物对土颗粒的包裹、胶结并形成稳定的骨架结构[5]。简文彬等[6]采用水泥-水玻璃对软土进行固化试验,并对固化土进行了微观机理分析。丁建文等[7]采用水泥-磷石膏对高含水率疏浚淤泥进行固化试验,研究了固化土力学性能的增长规律。采用化学固化方法改良后的淤泥固化土在一般情况下可达到工程强度要求[8],但试样水稳定性较差、脆性破坏、易出现裂缝等问题仍然存在,尤其在复杂应力环境下(如暴雨、洪涝、堤岸等)的变形和稳定性的演化规律尚未得到充分认识[9]。对此,已有学者考虑对淤泥固化土进行纤维加筋复合固化。李赛等[10]采用固化剂对淤泥进行固化,同时还加入了玉米须加筋固化,对试样的抗剪强度变化进行了系统性的研究。陈瑞敏等[11]研究了CSFG-FR(cement slag flyash gypsum-fiber reinforced,水泥-矿渣-粉煤灰-石膏-纤维加筋)共同作用下对软土的改良机制,从力学特性、渗透性能、微观结构、化学分析、固化机理等多个维度分析了纤维加筋与固化剂作用下的固化效果。Tang等[12]将聚合物纤维掺入水泥基固化软土中,发现其不仅提高了水泥土的强度,而且将脆性破坏改善为塑性破坏,延缓了土体的开裂。Carruth和Howard[13]发现纤维的掺入在提高土体弹性模量的同时还增加了土体的延性。Khattak和Alrashidi[14]通过室内劈裂与耐久性试验发现纤维的掺入增强了土体的抗拉强度,同时减少了土体的收缩开裂。然而,大部分学者重点关注于固化土的力学强度提升,但少有人着眼于淤泥固化土的本构模型研究。胡亚元等[15]在一系列室内三轴试验的基础上建立了邓肯-张模型,虽能一定程度上刻画出应力-应变曲线的非线性特性,但受限于该模型的数学形式,因此尚无法反映固化土在试验中有可能出现的应变软化现象。

纤维加筋淤泥固化土作为一种特殊的岩土体,具有明显的黏-弹-塑性特征,有时还可能表现出应变软化或硬化的流变特征[16]。鉴于此,本文以该土为研究对象,开展一系列不同纤维掺入比与围压的不排水三轴试验。拟在室内试验数据的基础上,建立一个可以反映应力-应变全过程的黏-弹-塑性本构模型,进而为工程实践提供设计依据与参考思路。

1 试验方案

1.1 试验材料

试验所用淤泥取自天津市某航道疏浚淤泥,其初始含水率为80%～90%。土样总体上呈近黑色,质地较软,流动状。所用淤泥的物理性质指标见表1。试验中液塑限的测试按《公路土工试验规程》[17]规定采用76g(g为重力加速度)锥式液塑限联合测定仪进行,颗粒级配采用马尔文仪器公司的Mastersizer 2000激光粒度分析仪测定,当淤泥中土颗粒直径>0.075 mm时划分为砂粒,直径为0.075～0.005 mm时划分为粉粒,直径<0.005 mm时划分为黏粒。

表1 疏浚淤泥的物理性质参数

所用纤维为长6 mm的聚丙烯纤维(PP),该纤维具备圆形横截面,直径为10 mm,且表面光滑平整,耐酸碱性和分散性好,强度较高。纤维的具体物理力学指标见表2。

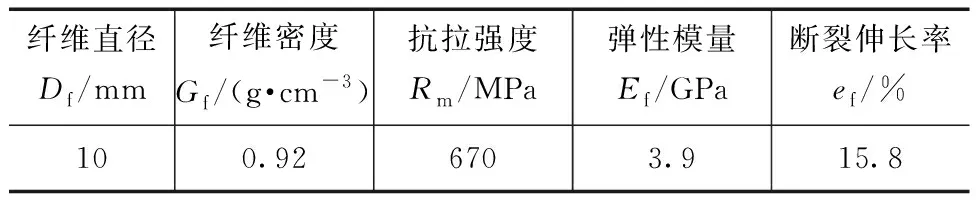
表2 聚丙烯纤维的物理性质参数

试验所用水泥为普通硅酸盐水泥P.O 42.5,由上海海螺水泥有限责任公司生产。其具体指标包括:初凝时间205 min,终凝时间260 min,体积安定性合格,3 d抗压强度平均值为23.9 MPa。

1.2 试验方法

纤维掺入比ρf与水泥掺入比ρc分别为

(1)

(2)

式中:mf为纤维的质量;mc为水泥的质量;m为所用疏浚淤泥的质量。

综合考虑疏浚淤泥加固效果以及水泥耗量,试验中确定水泥掺量为10%,水灰比为1∶0.55。参考陈瑞敏等[11]加固淤泥时超出临界纤维可能产生的负效应,以及为与胡亚元等[15]提出的邓肯-张模型进行对比验证,综合考虑后确定纤维掺量分别为0、0.1%、0.2%、0.3%、0.4%。

按上述掺量制备25组纤维加筋淤泥固化土试样,每组设置平行试样3个,具体试样制备方案见表3。制样时,为保证PP纤维在固化土中可以均匀分布,需将纤维事先分散成束状单丝,随后逐渐将其加至固化土中。按1∶0.55的水灰比调配浆状水泥,人工搅拌后加入淤泥试样中以便于混合。使用小型搅拌机充分拌匀混合样,装样时分层振捣压实,制成半径为39.1 mm、高为80 mm的标准三轴试样。室内24 h后脱模成型并放入标准养护箱中进行养护7 d,试验前一天采用真空抽气装置进行抽气饱和。具体的制样和试验步骤详见《水泥土配合比设计规程》(JGJ/T 233—2011)[18]。

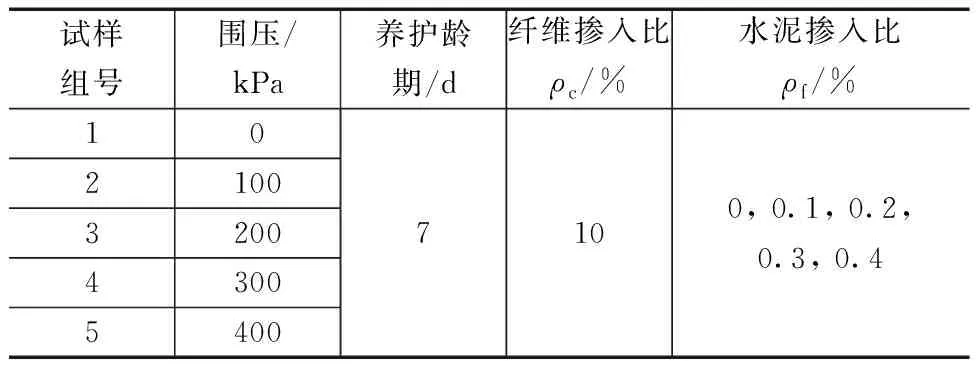
表3 试样制备方案

采用QSY-30型应力应变控制式全自动三轴仪进行三轴剪切试验。该仪器主要包括控制及可视化微机终端、数据采集仪、三轴压力室、应变控制器、加载架、进出水口和升降板等主要部件组成,具体仪器和试样剪切过程如图1所示。在试验过程中,可由微机终端实现全过程的操作与控制,并同时进行数据的自动化采集。试验开始后,将饱和试样装入三轴仪器的压力室中,设定围压进行固结并待其完成,以0.01%/min的恒定速率对试样进行不排水剪切,当剪切至预先设定的12%最大轴向应变时,试验自动停止。值得指出的是,当三轴剪切试验时的围压设置为0 kPa时,此时的试验条件相当于无侧限条件,得出的峰值强度为无侧限抗压强度。

2 试验结果分析

2.1 纤维掺量对强度及变形特性的影响

不同纤维掺量在围压为300 kPa下的应力-应变曲线如图2所示。从试验结果可以看出:在相同的围压下,随着纤维掺量的增加,淤泥固化土破坏时的峰值强度显著增加;破坏应变大致不变,集中在3.6%左右。对于不含纤维的试样而言,在破坏后阶段曲线陡降明显,呈现脆性破坏状态,破坏迅速。掺入纤维后,随其含量增加,破坏后阶段曲线下降缓慢,基体开裂后抵抗变形的能力依然存在。同时,在较高纤维掺量下,试样表现出了应变软化的现象,其黏性性能显著增强,残余强度依次提高。

图2 不同纤维掺量在围压为300 kPa下的应力-应变曲线

2.2 围压对强度及变形特性的影响

纤维掺量为0.3%的试样在不同围压下的应力-应变曲线如图3所示。从图3中可以看出,固化土试样的强度随着围压的增加而逐渐提升。当围压从0 kPa(无侧限)增加到400 kPa时,峰值强度分别为346.41、562.16、664.18、784.24、892.38 kPa,对应的破坏应变分别为2.34%、3.98%、3.72%、3.76%、3.91%。同时,观察试样在不同围压下的应力-应变曲线形态,也可以看出其在剪切过程中也明显表现出了流变特性,在破坏后阶段,随着围压的不断增加,应变软化现象呈逐渐显著的迹象。

图3 试样在不同围压σ3下的应力-应变曲线(ρf=0.3%)

2.3 固化土强度演化规律

不同纤维掺量的无侧限抗压强度如图4所示,从图4中分析可得,随着固化土中纤维掺量的不断增加,试样在无侧限抗压条件下的峰值强度也随之逐渐提升,依次为204.32、234.42、275.49、346.41、422.86 kPa。这是因为当掺入纤维时,纤维通过三维网络发挥桥梁作用,有效抑制破坏面的发展,提高了无侧限抗压强度。

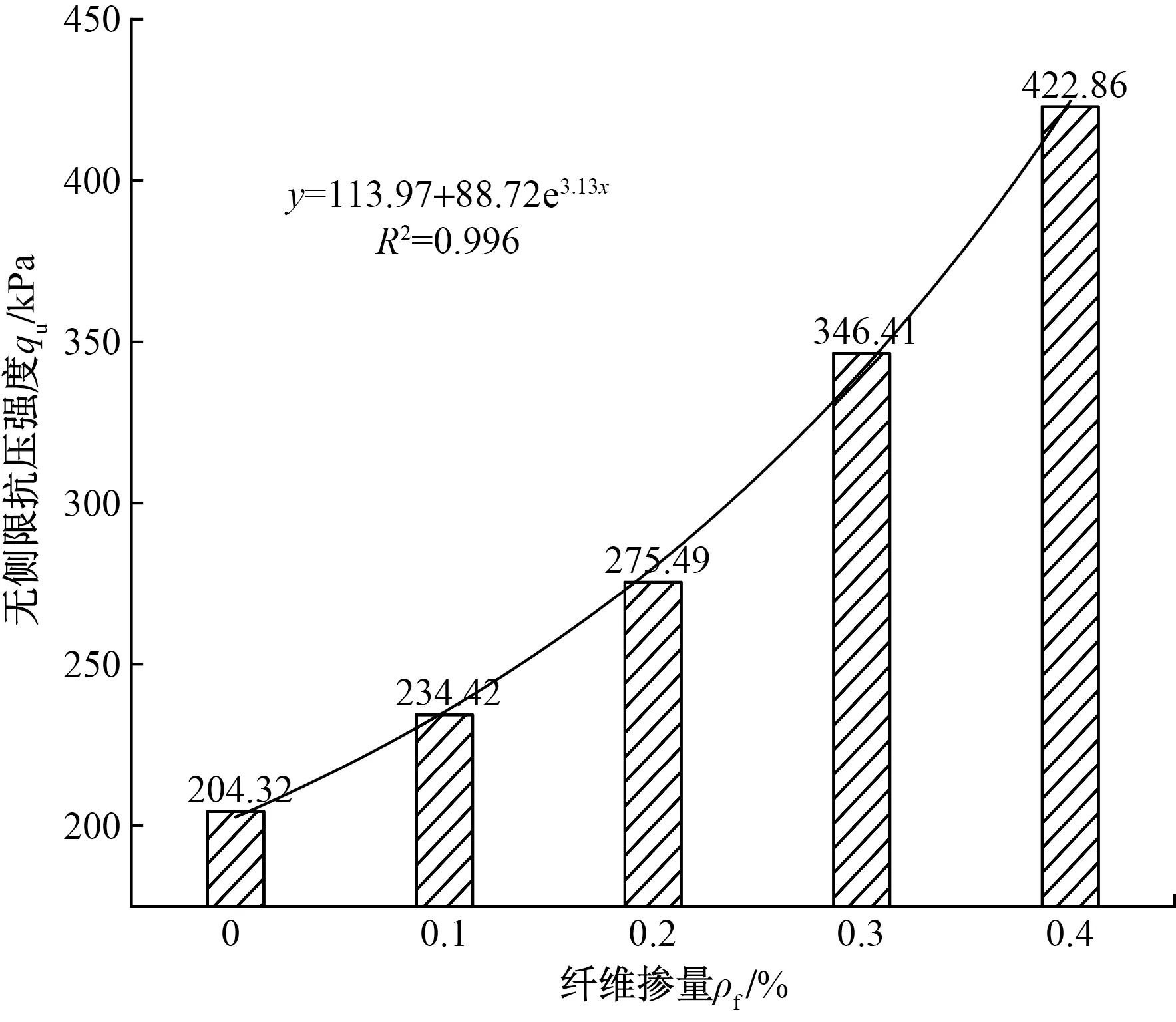
图4 不同纤维掺量的无侧限抗压强度

根据所得到的试验结果,对无侧限抗压试验下所得的峰值强度进行拟合,可得到不同纤维掺量条件下的强度演化方程:

qu=113.97+88.72e3.13ρf

(3)

纤维掺量在不同围压下的固化土摩尔圆和强度包络线如图5所示。在该围压下,强度包络线大致呈一直线,这可能是由于固化土具备相对较大的结构屈服应力,在剪切过程中,作用于固化土的围压未使其内部的胶结结构发生明显的破损。固化土内在的结构屈服应力比和外界施加的法向应力共同决定了其强度包络线的形态。

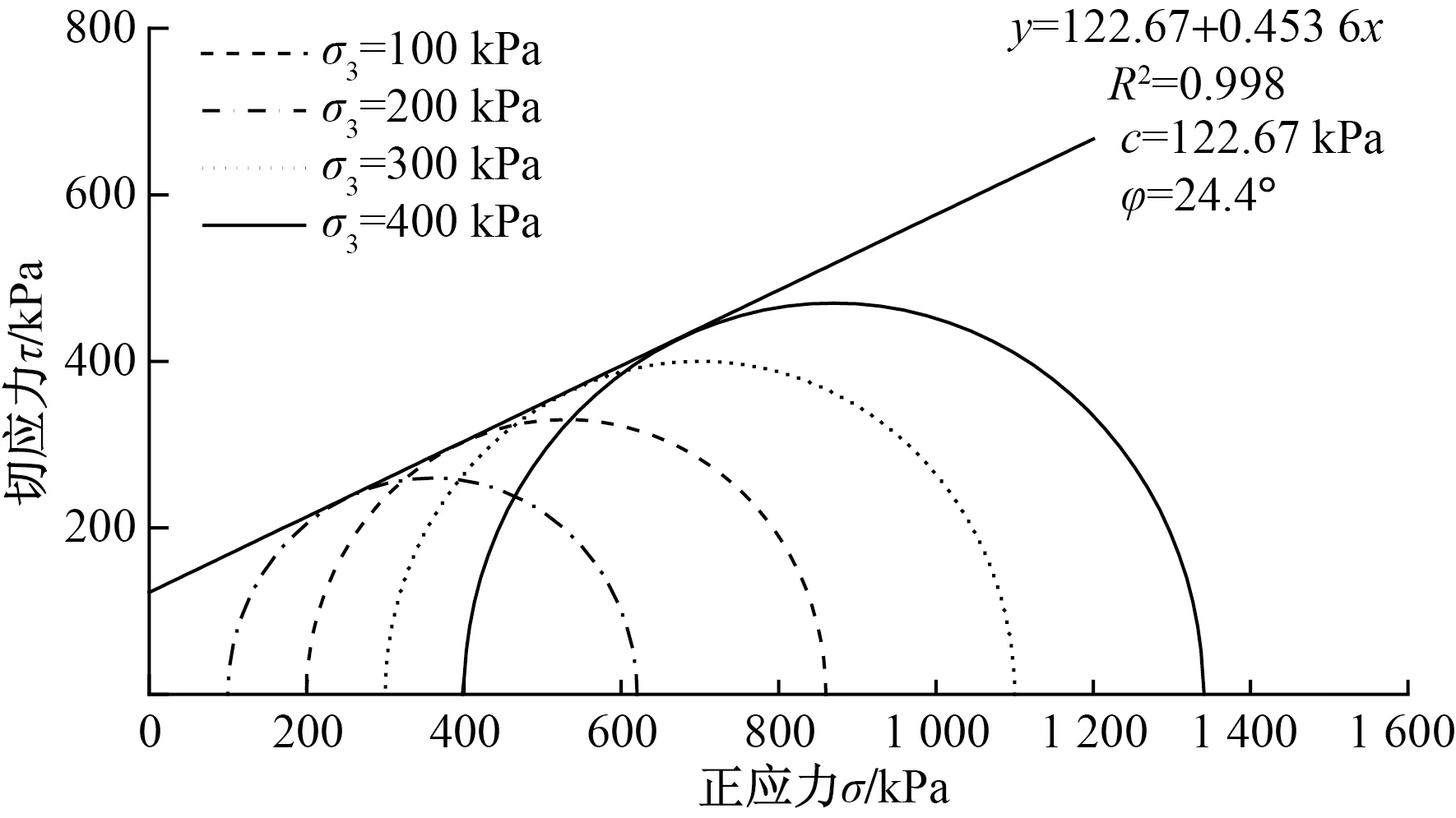
c为黏聚力;φ为内摩擦角图5 围压为300 kPa下的摩尔圆和强度包络线

根据三轴剪切试验的结果,结合摩尔-库仑强度准则进行分析。不同纤维掺量下的固化土强度参数见表4。从表4中可以看出,纤维的掺入基本上不影响试样的内摩擦角φ,总体平均值基本保持不变。当纤维掺量从0增加到0.4%时,固化土的黏聚力c从43.83 kPa增加到172.04 kPa,增幅随纤维掺量的提高而逐渐增加,可能存在幂函数型的强度关系。这可能是由于分散的短纤维在固化土中呈三维网状分布,对土颗粒及水化产物形成加筋作用。当土体受到外部剪切作用时,三维纤维网随之产生反作用力,如纤维本身的拉应力、纤维-骨架的界面摩擦力等,从而抑制试样的破坏趋势。

表4 不同纤维掺入比的淤泥固化土强度指标

3 淤泥固化土本构关系

3.1 应力-应变全曲线特征

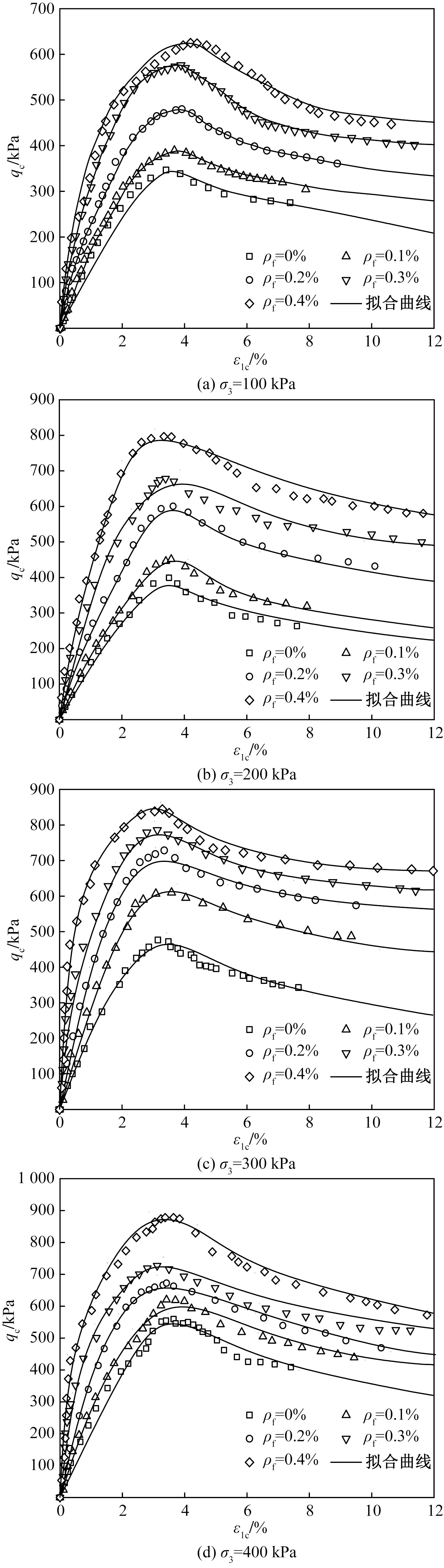
固化土应力-应变关系可在单轴或三轴围压应力条件下测得,可以较为完整地反映试样在各个受力阶段的变形规律、破坏特征和力学性质等。根据室内试验所测得的数据成果,固化土的典型应力-应变曲线特征可以总结绘制成图6。总体上,应力-应变曲线可分为弹性阶段、塑性阶段和黏性流变阶段,分别对应图中的OA、AB、BC段。

第Ⅰ阶段,弹性OA段,此时应力处于初始加载阶段,应力水平较低(qc

第Ⅱ阶段,塑性AB段,应力随应变呈现出非线性增长的规律,具体表现为应力-应变曲线斜率逐渐发生改变。自A点起固化土内部土颗粒逐渐发生破裂,结构开始产生损伤,至B点固化土到达峰值强度,固化土结构完全损伤。当应力超过弹性极限时(qc>qec),固化土的应力-应变曲线上的斜率逐渐减小,土中颗粒发生破损,孔隙不断被压密,其变形不可再恢复,因而属于塑性变形阶段。

第Ⅲ阶段,黏性流变BC段。在一定围压范围内,固化土达到峰值强度后,由于结构尚未完全破坏,试样内纤维加筋及骨架作用力同时作用而发挥残余强度,此时应力-应变曲线表现为应变软化型特征,曲线由陡变缓,斜率由大变小,进而逐渐达到残余强度值C点。此时固化土处于残余阶段,试样仍然具有一定强度,随着围压的逐渐提升,试样的力学强度(如峰值应力和残余应力)可能在一定程度上相应提高。在该阶段内,相同时间内的变形可能因应力-应变曲线表现出来的流变特征(如应变硬化或应变软化)而具备不同的变形速率,因而一定程度上属于黏性变形阶段。

3.2 应力-应变全曲线方程

为了描述纤维加筋淤泥固化土三轴应力-应变曲线的非线性特征,尤其是在不同阶段所表现出来的典型的黏-弹-塑性特征,考虑引入Popovics模型[19]对其进行全过程的刻画,即

(4)

式中:ε1u为无侧限应变;n为模型参数。

对室内试验所得到的数据进行深入分析,同时结合Popovics模型的相关研究基础,考虑对Popo-vics模型进行修正,以更好地描述刻画纤维加筋淤泥固化土的黏-弹-塑性应力-应变特征。修正后全曲线方程为

qc=Eecε1c, 0<ε1c<εec

(5)

(6)

(7)

式中:下标c表示三轴应力状态;qc为广义剪应力;nac=(Eec/Euc-qec/quc)/(Eec/Euc-1),修正Popo-vics模型含5个模型参数,分别为Eec、qec、Euc、quc、nbc,Eec为初始模量,Euc为应力峰值割线模量,qec为弹性极限强度,quc为峰值强度,nbc为第二段三轴应力下模型参数,它们均为无侧限抗压强度qu和围压σ3的函数。

3.3 模型参数的确定

对在三轴试验中得到的数据进行分析,首先将不同纤维掺量下的淤泥固化土在围压分别为100、200、300、400 kPa时的峰值强度quc和弹性极限强度qec进行线性拟合,如图7、图8所示,并得到其关系式为

图7 quc和σ1u、σ3的关系

图8 quc和qec的关系

quc=1.723σ3+1.152 8qu

(8)

qec=1.132quc-227.873

(9)

将式(9)代入式(8)中可得

qec=1.132(1.723σ3+1.152 8qu)-227.873

(10)

为准确刻画岩土体在应力-应变曲线中表现出的非线性特性,引入Janbu公式来表征初始模量Eec与围压σ3间的关系,即

(11)

式中:pa为大气压强,取pa=100 kPa;k、n分别为随无侧限抗压强度变化而变化的模型参数(图9、图10),可由式(12)、式(13)计算得到。

图9 Eec和σ3的关系

图10 模型参数k、n与qu的关系

n=0.201 5(qu/pa)-0.375 71

(12)

k=110.2+e0.197(qu/pa)

(13)

将模型参数k、n代回Janbu公式,可得

Eec=[110.2+e0.197(qu/pa)]pa(σ3/pa)0.201 5(qu/pa)-0.375 71

(14)

纤维加筋淤泥固化土的应力峰值割线模量Euc与初始模量Eec之间存在良好的线性关系,可假设他们间的关系如式(15)所示。不同围压下的应力峰值割线模量与初始模量的关系如图11所示,则C可表示为式(16)。

图11 Euc与Eec的关系

Euc=CEec

(15)

C=0.178 4(σ3/pa)+0.744 1

(16)

类似地,nbc与σ1u间的关系可表示为

nbc=A(qu/pa)+B

(17)

式中:A=-0.179 3(σ3/pa)+0.352 8;B=3.053 2(σ3/pa)-0.757 2。

如图12所示,由Popovics模型表示的黏-弹-塑性本构模型可以较好地反映出纤维加筋淤泥固化土的三轴应力-应变关系。

图12 本文模型在不同围压σ3下的拟合情况

纤维加筋淤泥固化土在围压σ3=200 kPa、纤维掺量ρf=0.2%下的不同模型效果对比如图13所示。胡亚元等[15]得到的实测数据显示,在该条件下,固化土的应力-应变曲线呈现类似双曲线的形态,没有典型的峰值应力与破坏后阶段。采用邓肯-张模型对其试验数据进行本构模型构建,但只能反映出固化土的弹塑性特征。本文所提出的修正Popovics模型较好地反映出实测应力-应变曲线的弹性、塑性和黏性阶段,全面反映了固化土在不同阶段表现出的变形特征,可为后续研究与工程应用提供参考。