基于L型流动仪的水泥砂浆流变参数预测

张宇靖, 朱吉鹏

(南京理工大学 理学院, 南京 210094)

在施工过程中,新拌混凝土的流变性质十分重要,它对于原材料的选用、配合比设计及泵送过程等方面都具有重要意义。而浆体作为混凝土材料的重要组成部分,其流变性质对混凝土的流变性有十分重要的影响[1-2]。Kabagire等[3]认为,自密实混凝土是由粗骨料与砂浆组成的两相材料,砂浆与自密实混凝土之间的流变特性具有很好的相关性。LI和Kwan[4]认为,新拌混凝土的流变性能在很大程度上取决于其砂浆的流变性质,故可以将水泥砂浆的合理设计作为混凝土配合比设计的前提。传统的评价砂浆流动性能的方法有微型坍落度筒法、L型流动仪、跳桌试验等,但这些方法只是对砂浆流动性的简单测定,不能准确地反映、评价其流变性[5]。流变学从一开始就是作为一门试验基础学科发展起来的,因此试验是研究流变学的主要方法之一[6]。实验室中采用流变仪来测定砂浆的流变性能。例如,利用同轴的双层圆柱筒,使内筒产生一定速度的转动,利用仪器测定内筒的转角,以求得两筒间的流体的牛顿黏滞系数等。但是流变仪器由于操作、价格等原因,使其在施工现场中使用不便[7]。因此寻找适合在现场测得或间接测得砂浆流变参数的试验仪器具有十分重要的现实意义。对于新拌砂浆流变性的描述,国内外学者一般采用Bingham模型来表征[8-9],该模型的流变参数有两个:屈服应力与塑性黏度。屈服应力即为使流体开始流动所需的最小剪应力,黏度为流体内部相邻流层之间的内摩擦力。二者可以定量描述新拌砂浆的流变行为。

许多研究者不断尝试寻找间接计算砂浆流变参数的方法[10-13]。Nguyen等[14]建议采用L-Box(L型流动仪)进行测定,他假设浆体为均匀单一流体,忽略惯性影响,分别对插有阻滞钢筋和未插阻滞钢筋的L型箱试验进行了理论推导,建立了L型箱的阻滞率h2/h1与流变参数τ0的关系,之后学者们对该公式进行了修正,并引入T500等时间参数预测塑性黏度[6]。同时随着计算机技术的发展,越来越多的研究人员开始采用数值模拟的方法对混凝土进行研究[15]。本文根据L型仪试验的结果,得到水平槽近端高度h1、远端高度h2、流动终止时间T7003个参数来计算屈服应力与塑性黏度,并利用计算流体力学专业软件Flow-3D对L型仪流动试验进行模拟,验证流变参数计算的准确性。

1 试验

1.1 原材料

采用强度等级为M25的水泥砂浆进行试验验证。砂浆主要由水泥、砂、水及外加剂组成;水泥采用某水泥化工厂的P.0 42.5硅酸盐水泥,物理性能指标见表1;砂选用Ⅱ级中砂,含泥量1.4%,其性能指标见表2;水采用普通自来水。

表1 普通硅酸盐水泥的物理性能指标

表2 中砂的物理性能指标

1.2 砂浆配合比

固定水泥砂浆水灰比为0.50,选取砂浆的灰砂比分别为0.7、0.8、0.9、1.0进行流变性以及流动度试验,并对计算公式进行验证,配合比设计按照绝对体积法进行计算。

1.3 试验方法

在25 ℃的室温下,按《混凝土外加剂应用技术规范》(GB 50119—2013)中测定混凝土外加剂相容性的试验方法拌制砂浆。

1.3.1 水泥砂浆流动度测试[17-18]

将L型箱水平放置,移去阻滞钢筋,关闭料斗挡板,将新拌砂浆装入L型箱装入竖直段,装满后刮平,之后提升料斗挡板,流动停止后,分别测量L型箱水平段近端和远端拌合物的高度h1、h2和流动时间t,至此试验结束[11]。可用边长为20 mm×10 mm的网格对L型箱的横向箱体侧壁进行划分,以更快更准确读取数据。最后计算得出屈服应力τ0和塑性黏度η。

1.3.2 水泥砂浆流变性测试

采用上海昌吉生产的NDJ-1型同轴旋转黏度计(用100 mL的玻璃烧杯代替外筒)测定砂浆的剪切速率和剪切应力。以剪切速率为横坐标、剪切应力为纵坐标,绘制散点图,选用Bingham流变模型拟合得出砂浆的屈服应力τ0与塑性黏度η。

1.4 模拟概况

采用三维模型全量分析[19],软件采用欧拉法将所研究区域划分为矩形结构网块,模型使用Auto CAD三维建模绘制,然后对L型仪进行网格划分,将模型分为两个大块,共计110 000个网格。L型仪箱尺寸、三维模型及网格划分情况如图1、图2(以x-z平面内网格为例)所示。

图1 L型仪箱尺寸

图2 L型箱三维模型

2 结果与分析

2.1 水泥砂浆流变模型的建立

1919年宾汉姆(E.C.Bingham)教授发现油漆属于同时具有塑性和黏性的物质。在此基础上,他把理想圣维南塑体和理想牛顿黏性体的流变方程合并称为宾汉姆体,其数学表达式为

(1)

砂浆的流变行为可近似用宾汉姆体描述,可采用宾汉姆流体方程拟合得出砂浆的屈服应力和塑性黏度[20]。固定浆体水灰比为0.50,不同灰砂比下水泥砂浆采用Bingham模型进行线性拟合得到的流变曲线如图3所示。拟合流变参数结果见表3。

图3 不同灰砂比水泥砂浆流变参数拟合曲线

表3 水泥砂浆的拟合流变参数

从表3可以看出,4组试验的拟合相关系数均大于0.970,拟合效果良好,表明4组砂浆的流变行为均符合Bingham模型。结合图3和表3中的数据可以看出,随着剪切速率的增加,不同灰砂比砂浆的剪切应力随之增加,且线性关系明显,随灰砂比增加,砂浆的屈服应力与塑性黏度不断减小,其中屈服应力的变化较大,当灰砂比由0.7增加到1.0时,屈服应力值由26.22 Pa减小到9.41 Pa,而4组试验的流变曲线基本平行,曲线斜率相差不大,即水泥砂浆的塑性黏度变化不大,略有减小的趋势,塑性黏度值由4.80 Pa·s减小到4.69 Pa·s。这是由于水泥净浆相较砂含量较多时,起到了更大的润滑作用,细骨料间摩擦力减小,故流变参数减小。

2.2 水泥砂浆流变参数的计算分析

2.2.1 屈服应力的计算

L型仪横向槽中浆体流动状态如图4所示。

图4 浆体流动状态

取流动结束后横向箱体内长度为dx的混凝土为例[8],如图5所示。

图5 新拌水泥砂浆单元体

由于测试时间较短(约1 min),因此忽略了流变学行为的任何触变情况。在底部及侧壁处,应力张量简化为一个标量:剪应力。当流体停止流动时,该区域的剪切应力等于屈服应力,该体积上的应力平衡方程为

(τ0l0dx)EFGH+(2τ0hdx)ADHE+BCGF=0

(2)

通常保留一阶项,式(2)化简为

(3)

(4)

积分得

(5)

故

(6)

式中:ρ为浆体密度,kg/m3;g为重力加速度,m/s2;l0为横向箱体的宽,m;h1为横向箱体近端高度,m;h2为横向箱体远端高度,m;L0为横向箱体的长度,m。

砂浆的L型仪流动度试验数据见表4,将该值代入式(6)计算得到浆体的屈服应力计算值,并与由旋转黏度计测得的浆体屈服应力实验值进行对比。将表4中浆体的屈服应力计算值与实验值作图比较,如图6所示。

图6 屈服应力计算值与实验值比较

表4 各组试验h1、h2、密度与屈服应力计算值

由表4中砂浆L型仪流动度实验结果可知,随灰砂比增加,砂浆的阻滞率逐渐增大,可见砂浆的流动性越来越好,水平槽两端的高度差逐渐缩小。图6表明,屈服应力计算值与测试值随灰砂比C/S的变化趋势有着良好的一致性,随灰砂比增加而减小。4组砂浆的屈服应力计算值均比试验值大,但两者在同一数量级,说明式(6)有其合理性。

2.2.2 塑性黏度的计算

目前还没有合适的公式可以通过L型仪的参数来计算砂浆的塑性黏度,此处借鉴混凝土的流动度试验计算塑性黏度的办法。Ferraris和Larrard[16]通过改良坍落度试验数据结果进行拟合,推算出黏度系数的计算公式

η=ρgt×25×10-3

(7)

式中:η为黏度系数,Pa·s;t为坍落度时间,s。

根据文献[14]的试验数据,分析浆体流至L型仪水平槽500 mm处所需要的时间T500和浆体流至L型仪水平槽700 mm处所需要的时间T700与η/ρ的关系,其中ρ为砂浆的密度,单位为kg/m3,如图7所示。

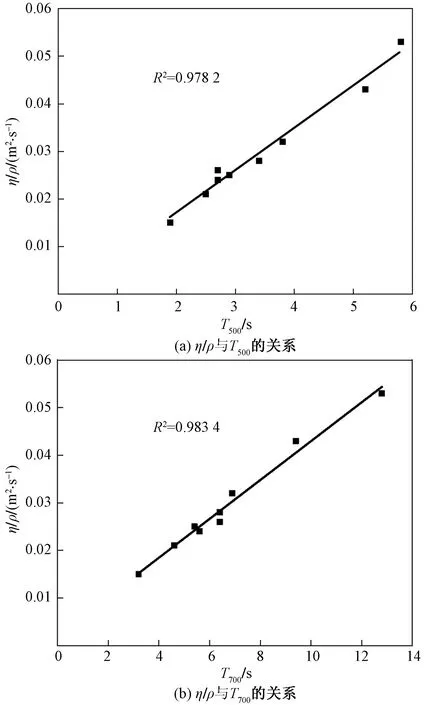
图7 η/ρ与流动时间T500、T700的关系

图7显示,浆体在L型仪水平槽的流动时间T500和T700与η/ρ的关系均呈线性关系,其中图7(a)的线性相关系数R2=0.978 2,图7(b)的线性相关系数R2=0.983 4,可知T700用于计算塑性黏度更为合理。以η=Aρgt+B为目标函数进行拟合可得

η=0.218×10-3ρgt+0.408×10-3ρ

(8)

砂浆在L型流动仪中的流动时间结果见表5,流动时间随灰砂比增加逐渐减小,说明砂浆有更好的流动性。将流动时间实验结果代入式(8)可得塑性黏度计算值η1,计算结果见表5。塑性黏度计算值与实验值保持一致的变化趋势,灰砂比越大,塑性黏度计算精度越好。可见砂浆流动性越好,模拟情况与实验操作更接近。图8显示出不同灰砂比下砂浆塑性黏度计算值η1与实验值η2的变化情况。可见无论是计算值还是实验值,塑性黏度随灰砂比的变化均不明显。

图8 塑性黏度实验值与计算值比较

表5 各组试验T700、密度与塑性黏度计算值

2.3 数值模拟验证

以第1、3组试验为例(第1组水胶比灰砂比为0.7,计算屈服应力为35.30 Pa,塑性黏度为10.92 Pa·s,第3组灰砂比为0.9,计算屈服应力为20.41 Pa,塑性黏度为7.88 Pa·s),将其实验结果与模拟结果进行对比,说明计算模型的合理性,两组试验在x-z平面内的模拟试验结果如图9所示,模拟的具体结果见表4、表5。

图9 各组砂浆拌合物在x-z平面内模拟结果

L型仪流动试验混凝土拌和物最终高度实验值与模拟值对比如图10所示。在重力作用下,浆体从L型箱垂直段向水平方向流动。由表4和表5中的数据可知,L型仪模拟流动高度与实际流动高度存在部分差值,但在可接受范围内,模拟所得的高度基本都小于实际的流动高度,可能是因为模拟过程中采用的是单相流模型,没有考虑细骨料摩擦及碰撞所产生的阻力。同时流动度越好,水平槽两点的高度差越小。第1组试验的流动时间为4.8 s,模拟流动时间为4.0 s,第3组试验的流动时间为3.2 s,模拟流动时间为3.5 s,二者十分接近,图10表明数值模拟的流动状态与试验结果接近,说明数值模拟可以较好地模拟L型仪中拌合物的流动,故屈服应力与塑性黏度的计算模型均有其合理性。

图10 各组砂浆拌合物最终高度实验值与模拟值对比

3 结论

通过对比黏度计测试结果与L型流动仪流动结果,可知两种实验方法可以互相验证,在施工现场,由于L型仪设备简易,操作简单,因此L型流动仪实用性更高,且节省了精密仪器的投入。

通过数值模拟与实际实验的对比分析,探究了L型仪试验的相关参数表征Bingham模型流变参数的准确性和合理性。无论灰砂比如何变化,模拟值均比实验值大,所以式(6)、式(8)中的系数不是唯一确定的,配合比等因素的变化会对计算结果产生影响。原因在于,砂浆是多种成分组成的混合物,但本文所采用的数值模型将新拌浆体看成均匀单一流体,实际流体中还会有骨料间的相互作用,这必然会导致一些误差的产生;另一方面,为了简化分析,数值模拟忽略了惯性作用对试验结果的影响。

借助流体力学软件Flow-3D可以对新拌水泥基材料流动性能进行研究,数值模拟的方法大大提高了工作效率,同时可以对试验条件进行准确控制,减少试验误差,数值模拟在流变学方面的应用有很大的发展空间,应该得到广泛的应用。