航路交叉点动态规划研究

武丁杰, 许凌宇, 朱 莉, 周鼎凯

(1.中国民用航空飞行学院 教务处, 四川 广汉 618307; 2.中国民用航空飞行学院 空中交通管理学院, 四川 广汉 618307)

航路是空中交通网络的重要载体,我国的航路网络错综复杂,其中航路交叉点是造成空域拥堵、航班延误、飞行事故的高发区域。如何对航路交叉点进行扩容,缓解拥堵,从而提高相应航路的运行效率,最大限度地发挥空域扇区的利用率,具有相当的研究价值。

目前国内外对航路交叉点问题进行了相应的研究。研究主要聚焦在航路交叉点构型研究、航路交叉点容量研究及疏导航路拥堵方面。在国外方面,Wang和Gong等[1]基于危险区和禁区限制上对航路构型进行了优化;Tran等[2]基于人工智能系统的基础学习管制员的管制偏好提出了交叉点拥堵疏导的解决方法;Zhi等[3]为了实现交叉点的扩容,使航班流安全高效地通过某固定交叉点,提出了一种紧凑的航班流构型。国内方面,张晨等[4]介绍了基于管型空域配置的交通复杂度管理;辛正伟[5]分析了航路交叉点布局问题的一般模型;戴福青等[6]建立了航路交叉点拥挤风险评估模型;申晨等[7]介绍了一种基于交通流邻近度的邻近映射生成复杂性估计值的空域容量评估方法;马玲等[8]提出了一种考虑交叉点复杂度的通行能力优化方法;刘豪等[9]提出了基于粗糙集基于属性约简的离群点检测方法(an outlier detection algorithm based on attribute reduction,AROD)算法的航路交叉点预测模型。

上述成果主要对航路交叉点的承载能力,航路网络的通行能力及容量预测等方面入手进行研究,较少聚焦于在未来基于航迹的运行(trajectory based operation,TBO)运行背景下,对航路构型进行变换从而实现扩容调配等策略手段进行研究。综上所述,本文基于上述的研究成果以及未来TBO环境下航路的运行特点,阐述了降维法的设计思路,并在此基础上引入协同决策的概念,使空管方充分考虑到航司与机场的诉求,建立改进型“井”字形模型。最后基于东部地区某空域航路进行实例分析,验证了变换构型的有效性和可行性,从而实现对航路交叉点资源的充分利用,提高交叉点的使用效率与通行能力,缓解因为航路交叉点拥挤而造成的航班延误和空域拥挤现象。

1 航路交叉点容量模型

1.1 问题描述与基本假设

降维法是指降低维度,但本文的航路维度并非传统意义上的空间维度,这里的维度指的是通过同一个交叉点的航路的条数。例如,两条航路经过一个交叉点为二维航路,三条航路经过一个交叉点即为三维航路。通过降低航路维度从而降低航路交叉点的复杂程度,起到减少飞行冲突的目的。降维法就是将三四维航路降维成类似于井字形构型的二维航路,使得交叉航路的复杂度降低,航班交叉汇聚的碰撞风险降低,同时分流扩容,使得使用降维法变换构型之后交叉航路点的容量大幅提高。

当空中交通流量增加时,此刻航路交叉点造成拥堵,为了缓解拥堵,在TBO运行的前提下,通过降维法变换为井字形构型,如图1所示。

图1 降维法示意图

通过建立分流航线,来缓解交叉点处的拥堵情况。为简化实际问题,做出如下假设。

假设1：航路最小间隔一经设定便不再更改。

假设2：航空器在交叉点处不发生碰撞。

假设3：航空器为单向运行,后机不允许超越前机。

假设4：空管采用TBO运行技术,能够准确计算出航空器经过各交叉点的时间。

1.2 交叉点容量

1.2.1 基本理论公式

(1)

式中:C为航路容量;N为服务航空的最大架次;T为服务的总时间。

航路容量分为动态容量ca和静态容量cb。

(2)

(3)

式中:X为航路长度;V为航空器的平均速度;D为管制间隔;ΔD为管制裕度。

1.2.2 单个交叉点情况下的航路交叉点容量(第一段航段)

根据何琛[10]可知,交叉航路交角与容量之间呈负相关,即随着航路交角的增大,航路容量逐渐减少。先假设航路交角α=90°,即两条航路为垂直状态时,推算单个交叉点容量,再加入三角函数得出不同角度下单个交叉点情况下的交叉点容量(图2)。

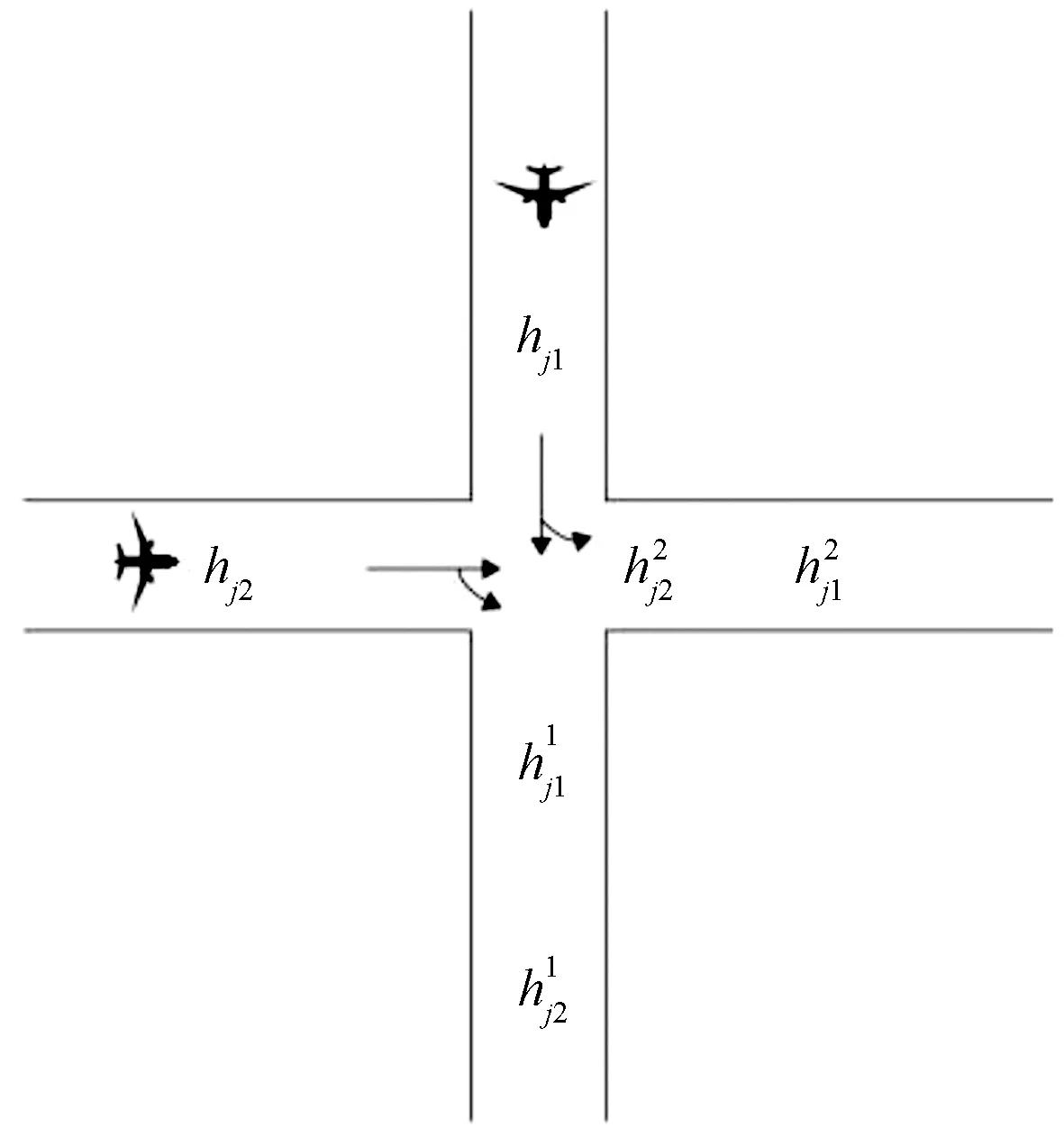
图2 单个交叉点航路构型(垂直)

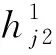
设管制预留间隔为L1,则

(4)

由式(2)和式(3)可得,在考虑预留间隔的情况下,动态容量和静态容量分别为

(5)

(6)

垂直状态时单个航路交叉点容量为

(7)

如图3所示,由三角函数可知航路交角为α的航路1与航路交角为90°的航路2之间为正弦函数。因此,在这两航段内的航空器架次的数量关系可近似看作正弦函数关系。一般地,单个航路交叉点容量为

图3 航路交角α示意图

(8)

1.2.3 井字形构型的航路交叉点容量

假设交叉航路航班流为hj1、hj2时,航班架次数越多,交叉口会发生拥堵,且计划航路1和2上的航班会造成等待,产生延误成本。因此,构建井字形航路,建立该交叉点临时航路1和临时航路2(图4)。

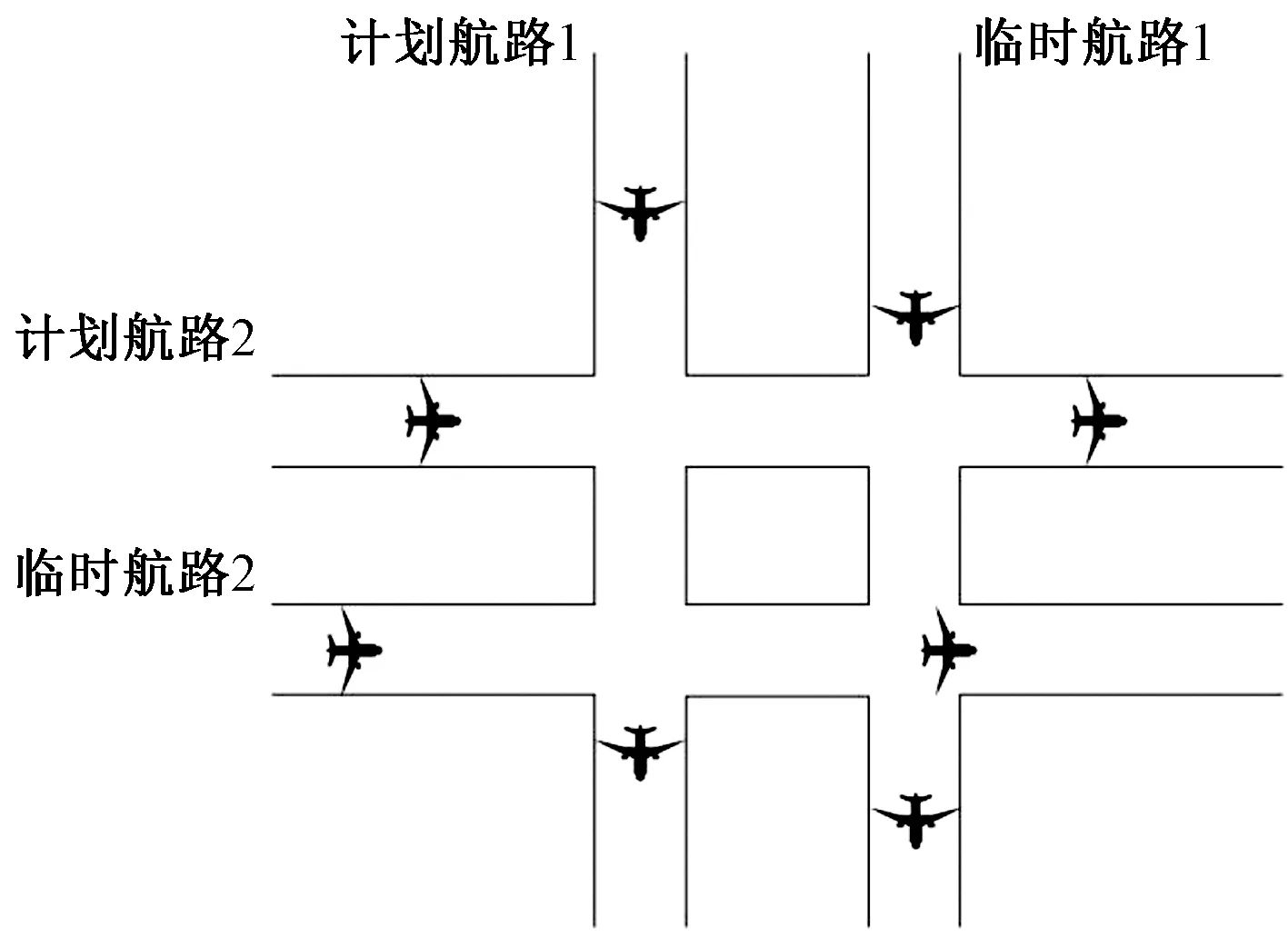
图4 井字型航路示意图

为简化模型,假设计划航路1和临时航路1为平行,计划航路2和临时航路2为平行。此时管制员可调配计划航路上的航班流,将其安排在临时航路上,以减轻原有交叉航路的运行压力。当只考虑计划航路1和计划航路2以及临时航路1时,管制员对不同预计时间进入交叉口的航班使用“先到先服务”(FCFS),根据式(8),可以得出两个航路交叉点容量为

(9)

综上所述,当使用井字形构型时,可以近似看作由两个双航段所构成的构型,因此垂直状态下井字形构型的容量为

(10)

根据式(8)和式(9),同理可得井字形构型容量为

C井=2C双=2(C′a+C′b)/sinα=

(11)

1.3 目标函数

当交叉航路发生拥堵时,变换为井字形构型后,对容量和航空公司延误成本会发生改变。因此,从航班总延误成本这个方面来建立目标函数。

模型符号定义:j1为计划航路1;j2为计划航路2;l1为临时航路1;l2为临时航路2;fj1为航空器使用计划航路1所造成的延误成本;fj2为航空器使用计划航路2所造成的延误成本;fl1为航空器使用临时航路1所造成的延误成本;fl2为航空器使用临时航路2所造成的延误成本;S为时隙总数;s为任意时隙 (s∈S);ts为任一时隙的起始时刻;P为航班总数;p为任一航班 (p∈P);np为航班p的载客数;ap为航班p的计划到达时间。

决策变量为

设全部航班总延误成本最低C1,则目标函数为

(12)

设旅客平均延误时间最小为C2,则目标函数为

(13)

1.4 约束条件

1)航空器唯一性约束。

(14)

(15)

式(14)和式(15)表示每个航班只进入一条航路以及只有一个时隙。

2)时隙唯一性约束。

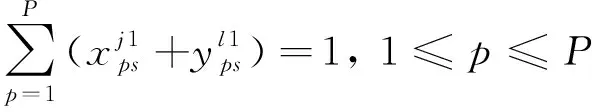
(16)

(17)

式(16)和式(17)表示每个时隙只能给一个航班使用。

3)容量的有限性。

(18)

(19)

式(18)表示单交叉点时,航路容量不大于航路计划容量;式(19)表示井字形构型时,航路容量不大于航路计划容量。

2 算例仿真

2.1 航路交叉点容量分析

图5为从民航局发布的AIP中截取的华东管制区域的部分航路,选取该图中的W45和A581两段交叉航路作为仿真空域。图6为简化后的航路示意图,两条航路之间的交角取α=60°。

图6 航路实例简化图

设在8:00—10:00早高峰之间有52个航班飞越。使用计划航路1飞越的航班数为28个,使用计划航路2飞越交叉点的航班为24个(表1和表2)。

表1 各航路航班数量

表2 航路信息

根据式(8),代入数据可以得出C单=57.6架次,则单航路交叉点每小时的容量为C单=28.8架次/h。

当航路变换为井字形构型时,此时标准管制间隔D=50 km[12]。根据式(11),代入数据可以得出C井=78.15架次,则井字形航路交叉点每小时的容量为C井=39架次/h。由以上结果可以得出,在同一时间段、同一飞行流量前提条件下,使用井字形构型交叉点相比于单个航路交叉点的容量提升了35.4%。因此,在TBO环境下使用降流法变换为井字形构型可以显著提高航路交叉点的容量,可以有效缓解交叉点拥堵情况,提高航空器的通过效率。

2.2 遗传算法求解

遗传算法的主要灵感来自达尔文的进化论模型和遗传学方面的知识。通过借鉴“适者生存,物竞天择”的思想,将需要解决的问题转化成进化模型,通过选择、交叉、变异等操作来选择精英解并进行保留,最终得到结果的最优解(图7)。

图7 遗传算法流程

以民航某交叉航路为例,根据该航路交叉点8:00—10:00航班数据进行仿真分析。在该时间段内,共有52个航班通过该交叉点,其中使用计划航路1的航班数量为28架次,使用计划航路2的航班数量为24架。根据管制部门发布的航路可用时隙表以及航班信息表(表3～表6),为航班进行排序以及选择航路。从而对比单个航路交叉点和井字形航路构型在延误成本和旅客平均延误时间方面的区别。

表3 航路可用时隙1

表4 航路可用时隙2

表5 使用计划航路1的航班信息

表6 使用计划航路2的航班信息

通过上述所提供的数据,使用MATLAB R2018b运行遗传算法,算法参数中设置种群大小为40,最大进化代数为200,交叉概率为0.9,变异概率为0.1。使用单个交叉点情况时,通过遗传算法,将使用计划航路1的28个航班和使用计划航路2的24个航班分配至两个航路的时隙表中。当使用井字形构型进行航班飞越时,此时多了两条临时航路1、2,管制员可通过临时航路的时隙将原本只能通过计划航路的航班进行分流到临时航路上。运行程序,得到遗传算法迭代曲线如图8所示。

图8 遗传算法迭代曲线

基于遗传算法求解所得到的结果表明,当使用单个交叉点构型时,航班总延误成本为300 300元,旅客平均延误时间为2.41 min;当使用井字型航路构型时,航班总延误成本为153 141.67元,旅客平均延误时间为1.14 min。从上述结果对比分析可得出,航班总延误成本降低了49%,旅客平均延误时间减少了52.7%,验证了算法的可行性。同时也表明在航路交叉点流量较大时,通过变换井字形构型,能够较好地疏通拥堵,降低航班的飞行成本及旅客的延误时间。通过该算法所得出的结果也可以为管制部门根据空域的实际情况选择合适的构型选择方案,并提供一些在TBO运行下管制方法的参考。

3 结语

本文建立了航路交叉点容量模型,通过对航路动态容量、静态容量的公式引出了单个航路交叉点及井字形构型的容量公式。同时,设置模型目标函数,比较两种构型在延误成本和延误时间方面的区别。基于对民航航路交叉点的仿真,对比两种构型,研究表明井字形构型可以显著提高航路交叉点容量,减少航班的延误成本和旅客延误时间。在TBO运行下,管制单位高空管制规则提供一些新的策略和思考。另外,本文对于降维之后的井字形航段只考虑了垂直情况,存在着局限性,在今后的研究中还要对井字形航段的不同角度情况进行讨论验证。同时,井字形航路构型有着飞行距离长、空域资源占用大等缺点,在接下来的研究过程中需要对该构型进行更加客观准确的研究。