高温下铝合金薄板面内轴压屈曲特性分析

卢松凯, 董毓利, 房圆圆, 齐建全

(华侨大学 土木工程学院, 福建 厦门 361021)

薄板的厚度远小于长度和宽度方向的尺寸,被广泛应用于航空航天领域中[1].铝合金具有易加工、易维修、耐腐蚀性好、强度高、成本低等优点,是航空航天器主要的结构材料[2-6].目前,对铝合金薄板屈曲性能的研究大多为常温稳定性[7-13],高温试验研究则主要集中于热屈曲性能[14-16],未见薄板高温下轴压屈曲稳定的试验研究,多体现在理论研究[17-20].

航空航天器中薄板结构受面内轴压作用,结构发生屈曲直至失稳,屈曲后薄板的受力性能和承载力随之发生变化.薄板屈曲试验对精度要求高,不易开展大量试验.因此,本文根据Yamaki[21]的铝合金薄板轴压屈曲试验,通过ABAQUS有限元分析软件建立铝合金薄板屈曲模型,分析高温下不同边界条件、不同截面尺寸及不同大小的几何初始缺陷对屈曲性能的影响.

1 铝合金方形薄板屈曲试验及有限元分析

1.1 试件及试验装置

试件采用边长为300 mm,厚度分别为1.24,0.99 mm的正方形铝合金薄板,试件参数[21]如表1所示.表1中：E为弹性模量;υ为泊松比.

表1 试件参数Tab.1 Test piece parameters

试验装置示意图,如图1所示.通过夹具(图1)将轴向压力传递到试件上,采用刀刃型夹具模拟简支边界条件(图2).开展轴压试验,最大负载为22.65 MPa,采用线性均速加载.在薄板前、后设置位移器,记录屈曲过程中的挠度变化.

图1 试验装置示意图Fig.1 Schematic diagram of test device

图2 刀刃型边界条件Fig.2 Edge type boundary condition

1.2 铝合金方形薄板有限元屈曲分析

1.2.1 常温下铝合金方形薄板屈曲分析 1) 有限元验证.通过ABAQUS有限元分析软件建立铝合金薄板模型,薄板模型被划分为10 000个长度和宽度均为3 mm的S4R壳单元,薄板材料为各向同性的线弹性材料(表1).运用弧长法对4种边界条件下的薄板进行模拟.首先,对铝合金薄板进行特征值屈曲分析,导出一阶屈曲模态[22];然后,复制模型,改用弧长法分析,设置最大荷载因子,并以弧长为总步长划分分析步,导入一阶屈曲模态作为薄板的几何初始缺陷进行模拟分析;最后,对比模拟与试验的结果.面内轴压试验有限元模拟值与试验值对比,如图3所示.图3中：P为荷载;w为挠度.

(a) 四边简支 (b) 加载边简支、非加载边固支

由图3可知：在结构屈曲前,荷载与挠度之间呈线性关系;结构进入屈曲阶段后,荷载与挠度的斜率发生变化,随着荷载增加,挠度呈非线性增大;固支边数量增加后,试验值与模拟值存在较小的误差,这是因为在加载边简支、非加载边固支工况下,试验中与荷载垂直方向的面内位移约束没有达到理想情况,在加载过程中,不能完全抵挡这部分位移,致使薄板产生较小的平面拉伸,降低了挠度;在四边固支工况下,试验中板边缘不能完全约束面内转动,导致后期屈曲产生的挠度略大于模拟结果.模拟值与试验值整体趋势保持一致,表明所建立的铝合金方形薄板屈曲分析模型符合试验要求,可以此模型开展后续的参数分析.

2) 几何初始缺陷.由于每块薄板存在不同程度的几何初始缺陷,即使在相同荷载作用下,结构的屈曲性能也不完全相同,因此,研究不同几何初始缺陷对薄板屈曲性能的影响.常温下不同几何初始缺陷的铝合金方形薄板参数,如表2所示.

表2 常温下不同几何初始缺陷的铝合金方形薄板参数Tab.2 Parameters of aluminum alloy square sheets with different geometric initial defects at ambient temperature

通过ABAQUS软件建立5个试件并进行分析,得到各工况的荷载与弧长的关系,提取弧长与挠度的关系,绘制不同几何初始缺陷下铝合金方形薄板的荷载-挠度曲线,如图4所示.

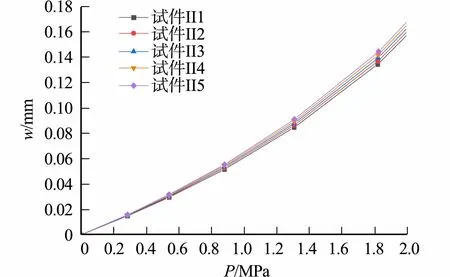
图4 不同几何初始缺陷下铝合金方形薄板的荷载-挠度曲线Fig.4 Load-deflection curves of aluminum alloy square sheets with different geometric initial defects

由图4可知：在不同几何初始缺陷下,铝合金方形薄板的屈曲变化保持一致;几何初始缺陷对挠度变化影响主要发生在薄板的屈曲变形阶段,在线弹性阶段各工况挠度变化保持一致,几何初始缺陷越大,挠度越大,挠度变化的斜率也越大.

综上所述,几何初始缺陷大小对结构屈曲阶段的挠度变化影响较大,对线弹性阶段的挠度影响较小;几何初始缺陷越大,挠度变化的斜率越大.

1.2.2 恒温加载下铝合金方形薄板屈曲分析 航空航天器在超音速飞行过程中除受外力荷载作用外,还受到温度场的作用.高温下材料容易发生劣化,导致承载能力下降.不同边界条件和几何初始缺陷在高温条件下的屈曲性能也各不相同.研究温度为500 ℃时,6061-T6铝合金薄板的屈曲性能,依据文献[23]中6061-T6铝合金热物理参数(表3)确定有限元分析模型的力学参数.表3中：θ为温度;λ为热传导系数;c为比热容;α为线膨胀系数;ρ为密度.

表3 6061-T6铝合金高温力学参数Tab.3 High temperature mechanical parameters of 6061-T6 aluminum alloy

1) 边界条件.不同边界条件下铝合金方形薄板的模型参数,如表4所示.绘制500 ℃下不同边界条件铝合金薄板的荷载-挠度曲线,如图5所示.

图5 500 ℃下不同边界条件铝合金薄板的荷载-挠度曲线Fig.5 Load-deflection curves of aluminum alloy sheets under different boundary conditions at 500 ℃

表4 不同边界条件下铝合金方形薄板的模型参数Tab.4 Model parameters of aluminum alloy square sheets under different boundary conditions

由图5可知：4种边界条件下的挠度变化保持相对一致;达到最大挠度时,试件BCT1挠度最大,为7.23 mm,随着固支边数量的增加,铝合金薄板受到的约束逐渐增大,挠度相应减少,试件BCT4的挠度最小,为2.97 mm;随着固支边数量的增加,屈曲阶段的荷载-挠度曲线斜率变小;四边固支薄板在达到13.29 MPa后,出现软化而发生“跳跃”,结构开始卸载,当荷载达到11.83 MPa后,结构开始“回弹”,进入强化阶段.

铝合金薄板在跳跃屈曲状态时的屈曲模态变化,如图6所示.由图6可知：结构最初受荷载作用呈现一阶屈曲模态的形式,随着荷载的增加,最大挠度区域开始向加载边偏移,之后屈曲模态逐渐向二阶屈曲模态转变,此时铝合金薄板发生“跳跃”,挠度随荷载增大而减小;随着荷载的增加,二阶屈曲模态逐渐趋于稳定,当结构处于“回弹”点时,二阶屈曲模态形式达到稳定,随着荷载增大,挠度继续增大.

(a) 铝合金薄板“跳跃”时 (b) 铝合金薄板“回弹”时图6 铝合金薄板在跳跃屈曲状态时的屈曲模态变化Fig.6 Buckling mode change of aluminum alloy sheet in snap buckling state

500 ℃下,铝合金薄板的荷载-挠度曲线的变化规律与常温下相似.绘制常温与500 ℃下不同边界条件薄板的荷载-挠度曲线,如图7所示.由图7可知：500 ℃下,无论在何种边界条件,铝合金薄板相同荷载作用下产生的挠度均大于常温下所产生的挠度,且500 ℃下的屈曲变化更为明显;与高温下四边固支薄板发生跳跃屈曲类似,常温薄板在达到上临界荷载30 MPa后,结构出现软化而卸载,又在达到下临界荷载26.56 MPa后,进入强化阶段;高温下铝合金薄板达到“跳跃”点所需的上临界荷载比常温下减小了16.71 MPa,达到“回弹”点所需的下临界荷载比常温下减小了14.73 MPa.

2) 几何初始缺陷.对500 ℃下不同几何初始缺陷的试件进行恒温屈曲试验,得到5种工况下铝合金薄板荷载与弧长,以及弧长与挠度之间的关系.通过两组数据绘制不同几何初始缺陷薄板的荷载-挠度曲线,如图8所示.由图8可知：薄板在不同几何初始缺陷下的荷载-挠度曲线的变化规律一致;前期线弹性工作阶段,5种几何初始缺陷下的薄板曲线相重合,而进入屈曲阶段后,随着几何初始缺陷的增大,薄板发生的挠度越大.

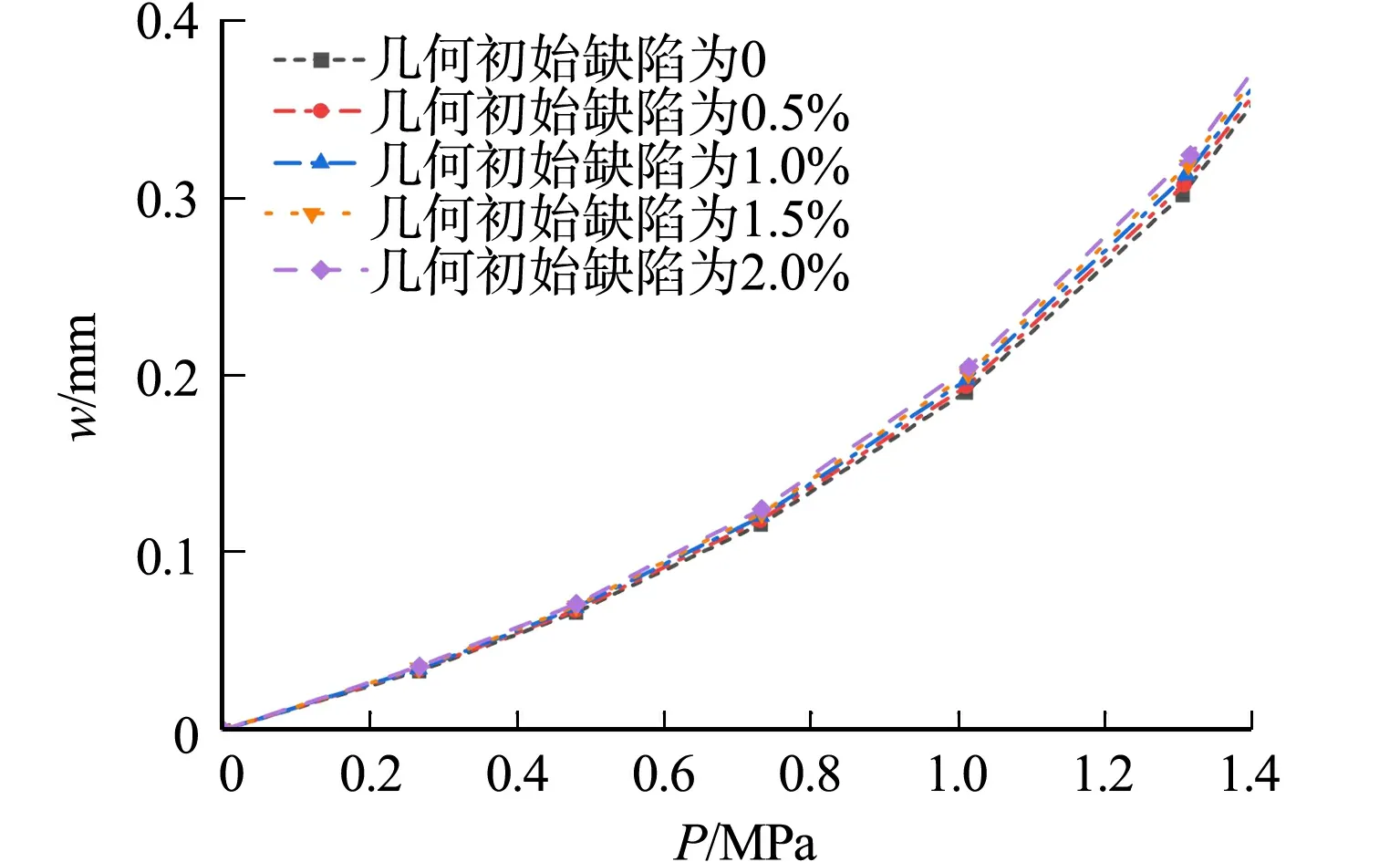
图8 500 ℃下不同几何初始缺陷薄板的荷载-挠度曲线Fig.8 Load-deflection curves of sheets with different geometric initial defects at 500 ℃

对比500 ℃和常温下的荷载-挠度曲线,如图9所示.由图9可知：500 ℃下铝合金薄板受荷载作用,初始缺陷相同时产生的挠度大于常温工况下的挠度,通过分析初始屈曲阶段的荷载-挠度曲线可以发现,高温下初始屈曲特征更为明显;初始缺陷对薄板屈曲时荷载-挠度曲线的斜率影响较大,初始缺陷越大,挠度变化斜率越大.

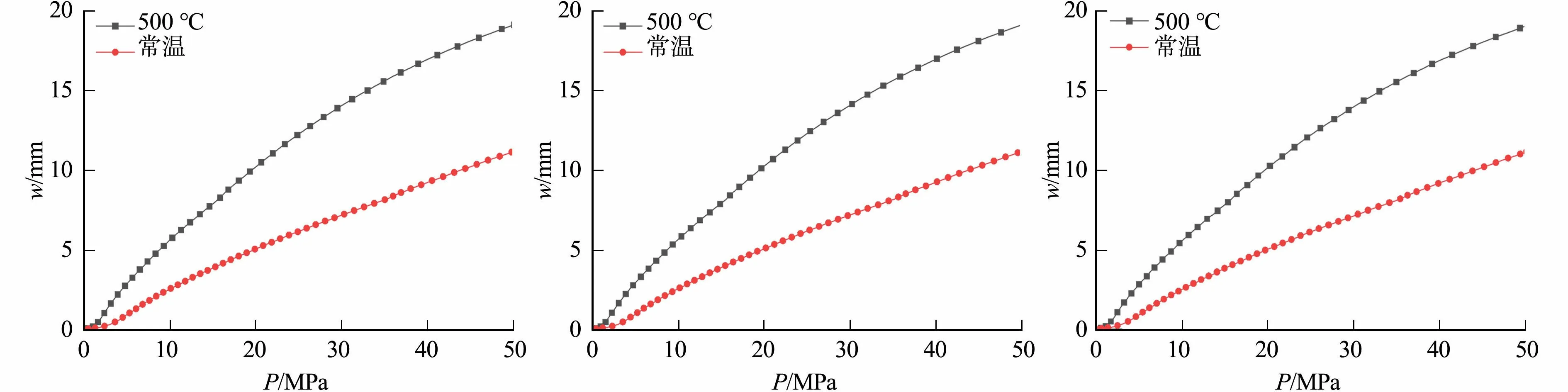
(a) 几何初始缺陷为0 (b) 几何初始缺陷为0.5% (c) 几何初始缺陷为1.0%

1.2.3 恒载升温下铝合金方形薄板屈曲分析 在升温过程中,结构的材料性质会随温度的改变发生变化.恒载升温试验中,选用文献[23]中的6061-T6铝合金作为试件材料.

1) 边界条件.恒载升温下不同边界条件薄板的模拟试验参数,如表5所示.表5中：Py为屈服荷载;Pa为结构施加荷载;θmax为发生大挠度所需温度;w500 ℃为500 ℃时产生的挠度.恒定荷载为各工况常温下屈曲荷载特征值的0.7倍,温度为0～500 ℃的线性升温模式.

表5 恒载升温下不同边界条件薄板的模拟试验参数Tab.5 Simulation experimental parameters of sheets with different boundary conditions under constant load heating

不同边界条件下铝合金方形薄板的荷载-挠度曲线,如图10所示.图10中：t为厚度.由图10可知：恒载升温下,4种边界条件下挠度的变化规律一致.由表5可知：与恒温不同,恒载升温时,加载边固支、非加载边简支产生的挠度最大,为1.90 mm,加载边简支、非加载边固支条件下产生的挠度最小,为1.46 mm.这可能是因为薄板受温度变化,弹性模量降低,产生热应力,薄板发生屈曲,同时板边缘的简支边界允许转动,抵消了部分热应力,而固支条件约束转动,无法抵消这部分应力,因此增大了挠度.

当薄板产生接近自身厚度大小的挠度(w/t>1.0)时,称薄板发生大挠度屈曲.由表5可知：加载边固支、非加载边简支在375 ℃最早发生大挠度屈曲,加载边简支、非加载边固支在450 ℃最晚发生大挠度屈曲.

2) 几何初始缺陷.将铝合金薄板常温下0.7倍的屈曲荷载特征值作为结构所施加的荷载.恒载升温下不同几何初始缺陷薄板的模拟试验参数,如表6所示.

表6 不同几何初始缺陷薄板的模拟试验参数Tab.6 Simulation experimental parameters of sheets with different geometric initial defects

模拟得到不同几何初始缺陷薄板的温度-挠度曲线,如图11所示.由图11可知：随着几何初始缺陷的增大,初始挠度逐渐增大,在温度达到410 ℃前,随着几何初始缺陷的增大,挠度也随之增大;当温度达到410 ℃后,几何初始缺陷越大,挠度越小.由表6可知：500 ℃时各工况的挠度相差不大;5种工况下进入大挠度屈曲阶段时的温度均小于410 ℃,试件II10最早发生大挠度屈曲,试件II6最晚发生大挠度屈曲,但由于初始缺陷相差不大,导致进入大挠度时的温度差距很小,可认为5种几何初始缺陷下进入大挠度屈曲时所需的温度均为375 ℃.

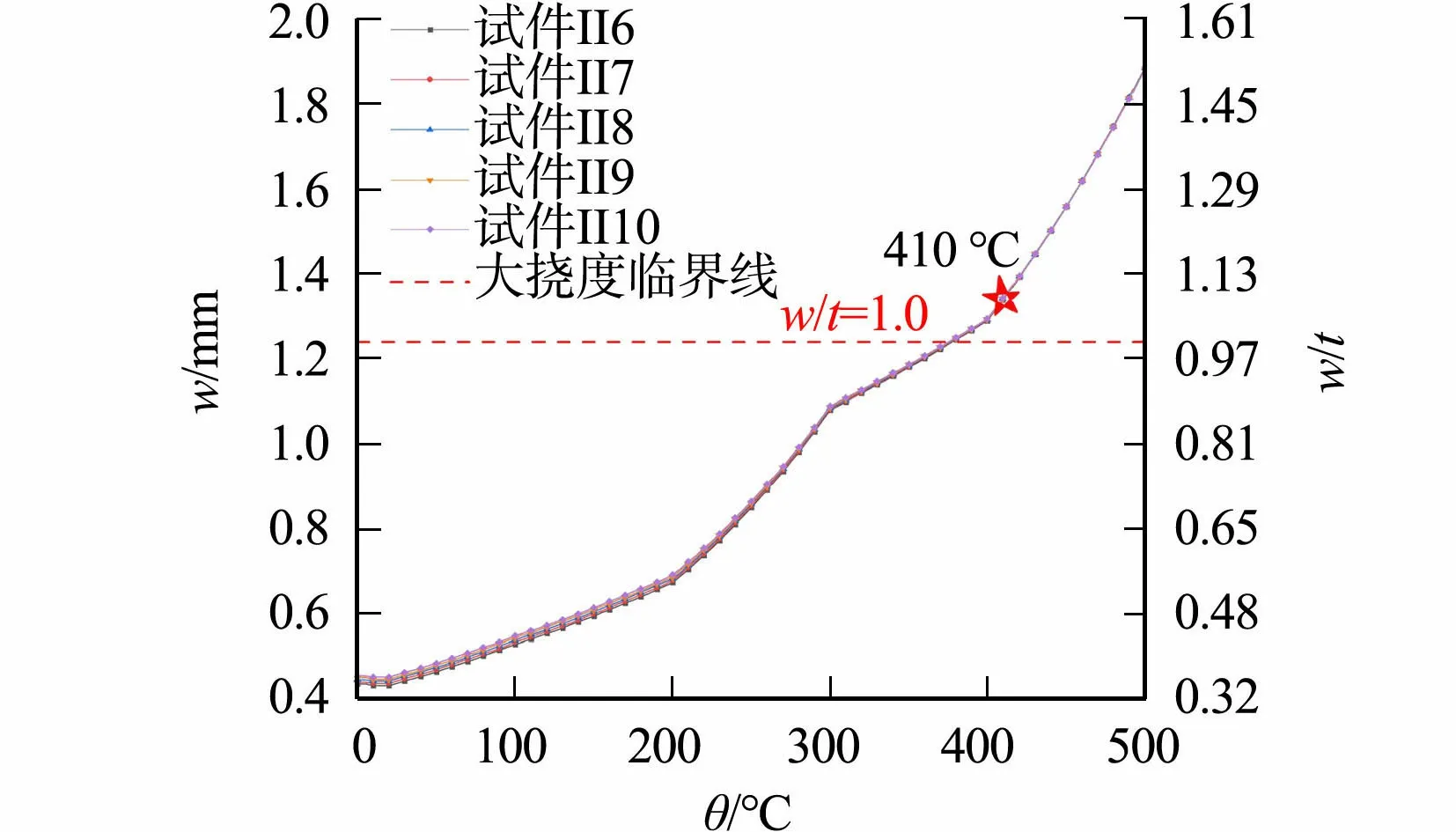
图11 不同几何初始缺陷薄板的温度-挠度曲线Fig.11 Temperature-deflection curves of sheets with different geometric initial defects

2 铝合金矩形薄板有限元屈曲分析

2.1 常温下铝合金矩形薄板屈曲分析

Yamaki[21]只研究了正方形铝合金薄板在不同边界条件下的屈曲性能,却没有研究不同长宽比的矩形薄板对屈曲性能的影响. 对四边简支下不同长宽比铝合金矩形薄板的轴压屈曲性能进行研究, 保持截面面积相同,材料性质见表1,不同长宽比下铝合金矩形薄板的设计参数,如表7所示.

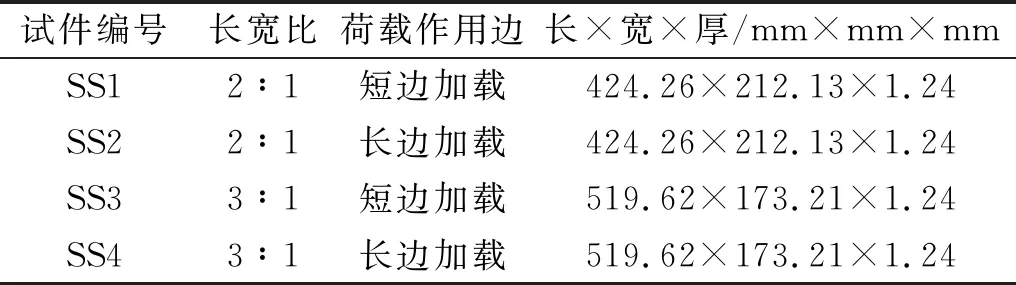
表7 不同长宽比下铝合金矩形薄板的设计参数Tab.7 Design parameters of aluminum alloy rectangular sheets with different length-width ratios

对试件SS1～SS4进行非线性有限元分析,与正方形截面不同,矩形截面有长边与短边的区别,因此对荷载作用于长边或短边进行研究,绘制不同长宽比下铝合金矩形薄板的荷载-挠度曲线,如图12所示.由图12可知：当长宽比相同时,荷载作用于长边时产生的最大挠度大于荷载作用于短边时;当长宽比不同时,荷载作用于长边时试件SS4产生的最大挠度大于试件SS2,荷载作用于短边时试件SS3产生的最大挠度小于试件SS1.

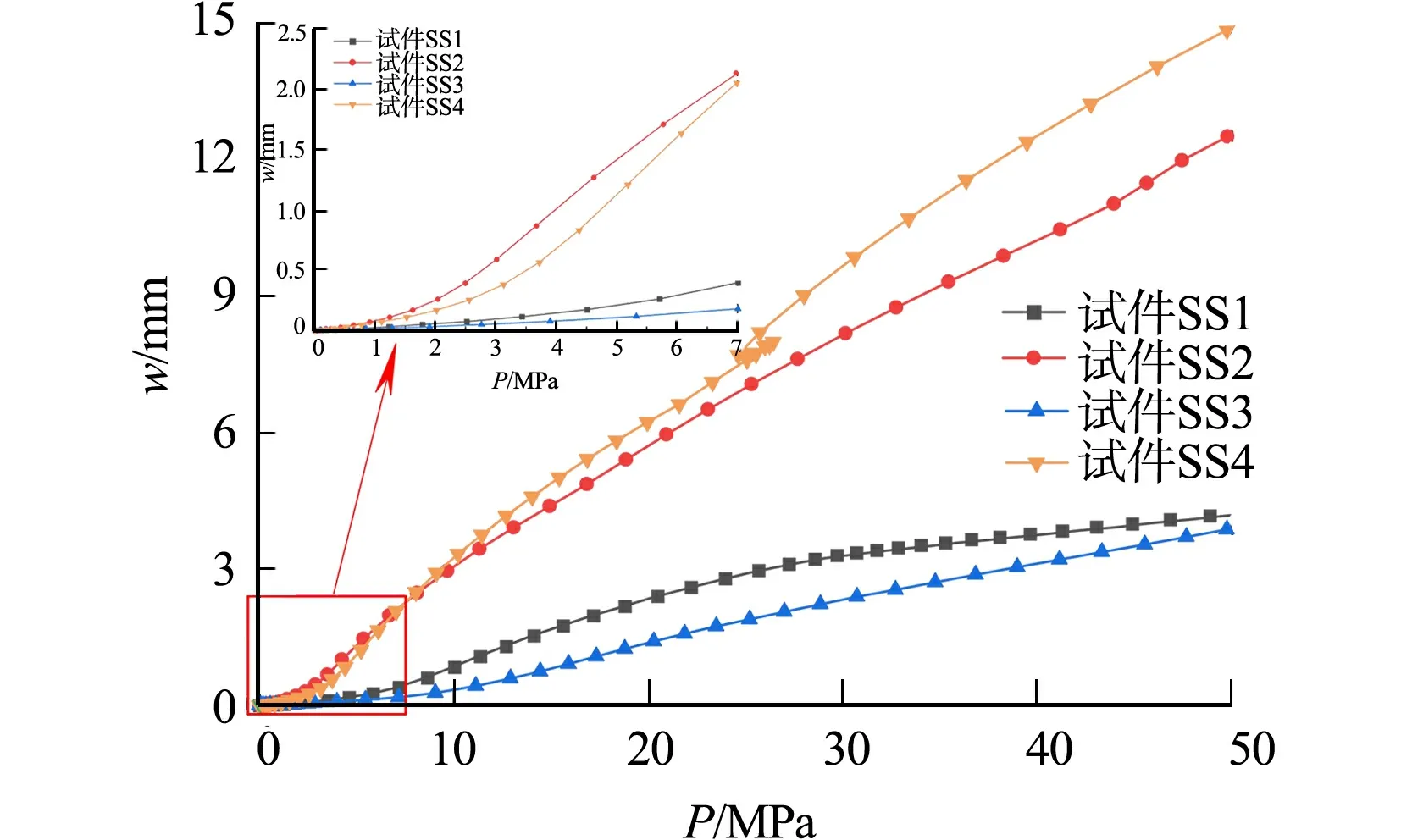
图12 不同长宽比下铝合金矩形薄板的荷载-挠度曲线Fig.12 Load-deflection curves of aluminum alloy rectangular sheets with different length-width ratios

在荷载达到50 MPa下,试件SS1～SS4的最大挠度分别为4.26,12.72,3.86,14.97 mm.综上可知,当荷载作用于长边时,长宽比大的工况产生的最大挠度较大;当荷载作用于短边时,长宽比小的工况产生的最大挠度较大;相同长宽比下,长边加载时产生的最大挠度较大.

2.2 恒温加载下铝合金矩形薄板屈曲性能分析

对铝合金矩形薄板进行高温下屈曲分析,研究四边简支下不同长宽比的铝合金矩形薄板在500 ℃下的屈曲性能.500 ℃下不同长宽比的铝合金矩形薄板的设计参数,如表8所示.

表8 500 ℃下不同长宽比的铝合金矩形薄板的设计参数Tab.8 Design parameters of aluminum alloy rectangular sheets with different length-width ratios at 500 ℃

对试件SST1～SST4进行模拟,得到500 ℃下不同长宽比的铝合金矩形薄板的荷载-挠度曲线,如图13所示.由图13可知：当长宽比相同时,长边加载的薄板产生的挠度大于短边加载产生的挠度;当长宽比不同时,长边加载下, 试件SST4产生的挠度大于试件SST2, 短边加载下,当荷载未达到25 MPa时,试件SST1产生的挠度大于试件SST3,当荷载达到25 MPa后,两个试件的荷载-挠度曲线几乎重合;短边加载下初始屈曲时荷载-挠度曲线的斜率比长边加载工况下小,长边加载下的挠度变化更明显.

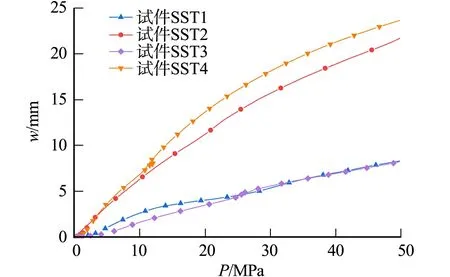
图13 500 ℃下不同长宽比的铝合金矩形薄板的荷载-挠度曲线Fig.13 Load-deflection curves of aluminum alloy rectangular sheets with different length-width ratios at 500 ℃

在500 ℃,50 MPa荷载作用下,试件SST1～SST4的最大挠度分别为8.16,21.80,8.07,23.80 mm.当长宽比相同时,长宽比为3∶1的试件SST3比试件SST4的最大挠度降低了66.09%,长宽比为2∶1的试件SST1比试件SST2的最大挠度降低了62.57%;当荷载作用边相同时,长边加载的试件SST2比试件SST4的最大挠度降低了8.41%;短边加载的试件SST3比试件SST1的最大挠度降低了1.11%.综上可知,荷载作用位置对屈曲挠度的影响较大.

常温与500 ℃下不同长宽比铝合金矩形薄板的荷载-挠度曲线,如图14所示.由图14可知：500 ℃下铝合金矩形薄板产生的挠度均大于常温工况产生的挠度,且屈曲过程特征更为明显;长宽比为3∶1的长边加载工况下,薄板发生跳跃屈曲,常温下试件SS4达到26.61 MPa后,结构出现软化而卸载,又在达到24.79 MPa后开始进入强化阶段;500 ℃下,试件SST4达到12.01 MPa后出现软化而发生“跳跃”,结构开始卸载,当荷载达到11.25 MPa后,结构开始“回弹”,进入强化阶段.对比常温与高温下跳跃屈曲的临界荷载变化发现,高温下铝合金薄板达到“跳跃”点所需的上临界荷载比常温工况下减小了14.6 MPa,达到“回弹”点所需的下临界荷载比常温工况下减小了13.54 MPa.

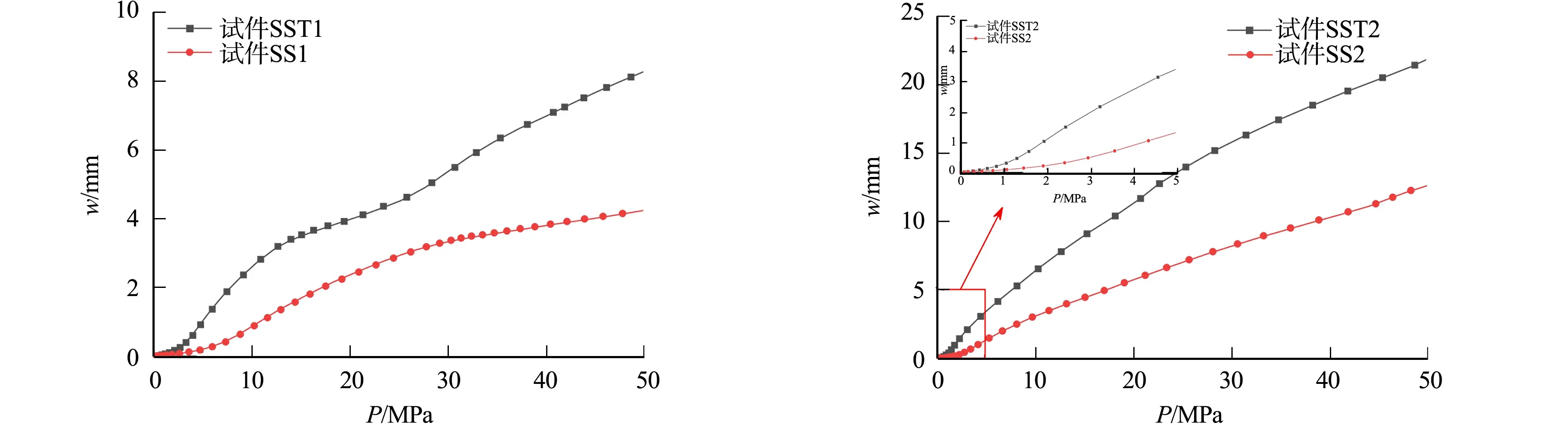
(a) 试件SS1,SST1 (b) 试件SS2,SST2

2.3 恒载升温下铝合金矩形薄板屈曲性能分析

将各工况下屈曲荷载特征值的0.7倍作为施加荷载,恒载升温下不同长宽比铝合金矩形薄板的模拟试验参数,如表9所示.通过模拟绘制不同长宽比铝合金矩形薄板的温度-挠度曲线,如图15所示.

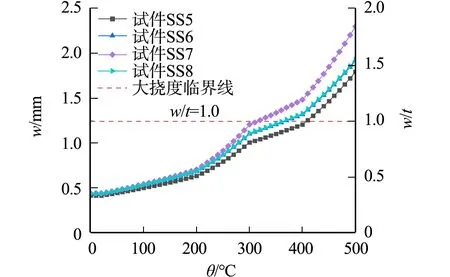
图15 不同长宽比铝合金矩形薄板的温度-挠度曲线Fig.15 Temperature-deflection curves of aluminum alloy rectangular sheets with different length-width ratios

表9 恒载升温下不同长宽比铝合金矩形薄板的模拟试验参数Tab.9 Simulation experimental parameters of aluminum alloy rectangular sheets with different length-width ratios under constant load heating

由图15可知： 4种工况下的挠度随温度变化趋势一致;当薄板的w/t>1.0时,挠度进入大挠度变形阶段. 由表9可知：当荷载作用边相同时,长边加载下试件SS5产生的挠度比试件SS7减小了0.51mm,短边加载下试件SS6产生的挠度比试件SS8减小了0.01 mm;试件SS7在365 ℃时最先发生大挠度屈曲,试件SS5最晚发生大挠度屈曲,所需温度为410 ℃.由此可知,短边加载下,长宽比对升温下薄板的挠度影响较小;长边加载下,选择长宽比较小的薄板能有效降低升温过程中产生的挠度.

3 恒载升温薄板的受力状态分析

恒载升温下,随着温度的增大,铝合金薄板的挠度随之增大,达到某一温度时,屈曲挠度的增速产生突变.有些温度-挠度曲线的突变温度点并不明显,需要通过特定方法进行判断.运用Mann-Kendall准则对恒载升温工况下,不同边界条件、不同长宽比及不同几何初始缺陷下的挠度突变的初始温度进行判断验证.

薄板屈曲过程中应变作为主要变形参数,表征了其工作状态与承载能力,从薄板截面中心线上选取5个点,结合应变数据实际含义,采用广义应变能作为受力状态特征参数.根据温度变化值与升温方式,计算应变点位置在发生温度变化时的广义应变能Eg.

1) 边界条件.运用Mann-Kendall准则,绘制试件BC5～BC8的广义应变能-温度曲线,得到轴压薄板受力状态特征点,如图16(a)所示.根据图16(a)可判断出4种边界条件下挠度增速发生初始变化的温度均在200 ℃.为确认所判断特征点的准确性,将所判断出的温度特征点在温度-挠度曲线中标记出,如图16(b)所示.根据图16(b)中标记的特征点位置可知,在200 ℃前后,挠度的变化速率发生了改变,证明所判断的特征点是正确的.

2) 长宽比.不同长宽比下轴压薄板的受力状态特征点和挠度模式突变特征,如图17所示.由图17(a)可知：不同长宽比下,挠度增速发生初始变化的温度均在200 ℃.根据图17(b)中标记的特征点位置可知,在200 ℃前后,挠度的变化速率发生了改变,证明所判断的特征点是正确的.

3) 几何初始缺陷.不同几何初始缺陷下轴压薄板的受力状态特征点和挠度模式突变特征,如图18所示.由图18(a)可知：不同几何初始缺陷下,特征点均为200 ℃.根据图18(b)中标记的特征点位置可知,在200 ℃前后,挠度的变化速率发生了改变,证明判断的特征点是正确的.

(a) 轴压薄板受力状态特征点 (b) 轴压薄板挠度模式突变特征图18 不同几何初始缺陷轴压薄板的受力状态特征点和挠度模式突变特征Fig.18 Characteristic points of stress states and sudden changes in deflection mode of axially compressed sheets under different geometric initial defects

4 结论

对面内轴压铝合金薄板屈曲试验进行模拟,研究高温下不同边界条件、不同长宽比及不同几何初始缺陷对薄板屈曲性能的影响.通过分析各工况的屈曲性能,得到以下3个结论.

1) 基于ABAQUS有限元软件对试件进行非线性有限元模拟分析,获得结构的荷载-挠度曲线,与试验结果吻合较好,证明数值模拟方法的可靠性和准确性.运用Mann-Kendall准则对结构受力状态进行分析,判断薄板屈曲过程中的突变点,通过子模式温度-挠度曲线对所判断的特征点进行验证,结果证明所判断特征点为挠度增长速率发生突变点,结论合理可靠.

2) 对于铝合金正方形薄板,恒温下通过提高边界条件的约束,能有效减小结构产生的挠度,提高结构的稳定性.恒载升温下,结构受到温度荷载作用,产生热应力,而板边缘的转动抵消了部分热应力作用,导致薄板挠度减小,加载边选择简支条件可有效减小挠度.在恒温下,几何初始缺陷对薄板屈曲发生阶段时挠度的变化速率影响较大,并且几何初始缺陷越大,挠度变化的斜率越大.在恒载升温时,温度达到410 ℃前,挠度随几何初始缺陷的增大而增大,温度达到410 ℃后,情况相反,但此时各工况下挠度大小差异不大.

3) 对于铝合金矩形薄板,恒温下长宽比相同时,短边加载可有效减小屈曲挠度;长宽比不同时,长边加载下选择长宽比较小的矩形薄板,短边加载下选择长宽比较大的矩形薄板可有效减小屈曲挠度,提高结构稳定性.恒载升温时,长边加载下选择长宽比较小的矩形薄板可有效减小屈曲挠度,提高结构稳定性,短边加载下长宽比对屈曲挠度的影响较小.