非局部Swift-Hohenberg方程的积分因子龙格库塔格式

汪亚楠, 蔡耀雄

(华侨大学 数学科学学院, 福建 泉州362021)

Swift-Hohenberg(SH)模型[1]最初是由Swift和Hohenberg在研究Rayleigh-Bénard对流时引入的,并且已经成为导致复杂模式形成的非线性动力系统的范例之一,其研究成果被广泛应用于复杂流体和生物组织[2-3].近年来,随着流体力学、反应扩散化学和生物学等学科的发展,非局部SH模型的研究吸引了众多学者的关注.Roberts[4]指出,将二维局部SH模型用作特定物理系统中空间模式演化的可靠模型是不够的,应使用非局部SH模型.2014年,Morgan等[5]首次提出带有非局部非线性项的SH模型,即

ut=-(Δ+1)2u+εu-uG*u2, (x,t)∈Ω×(0,T].

(1)

非局部项G*u2的定义为

卷积核G满足以下3个条件：1)G(x)≥0,对于任意的x∈Ω;2)G是Ω-周期性;3)G(x)=G(|x|)

是一个给定的径向对称函数.

非局部SH方程(式(1))可看作能量函数E(u)的L2梯度流,有

(2)

关于局部SH方程的理论和数值研究已有大量的优秀成果[6-7],而关于非局部SH方程的研究工作还十分有限.非局部SH方程中的非局部和非线性项给研究带来巨大挑战.Firth等[8]提出非线性光学系统的非局部模型.Purwins等[9]提出介质气体放电动力学的非局部模式.Du等[10]提出非局部算子的向量演算.Zhang等[11]提出一个带有拉格朗日乘子的守恒型非局部 SH方程.Weng等[12]利用傅里叶谱方法求解带有非局部非线性项的SH方程.

近年来,作为求解偏微分方程的有效数值方法,积分因子龙格库塔法受到广泛关注.Ju等[13]提出关于半线性抛物方程的保极值原理的积分因子龙格库塔方法.Ahmed等[14]提出关于非齐次边界条件系统的高阶积分因子法.Zhang等[15]提出保守Allen-Cahn方程的显式三阶保结构格式.Nan等[16]提出求解非局部Allen-Cahn方程的高阶极值原理积分因子龙格库塔方法.基于此,本文结合积分因子龙格库塔法和谱方法[17]对式(1)进行有效求解,并提出4种快速有效求解非局部Swift-Hohenberg方程的数值格式.

1 数值格式

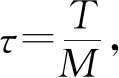
1.1 预备知识

空间区域Ω=[-a,a]2上的网格剖分为

为了求解周期边界条件下的非局部SH方程(式(1)),基于谱方法的相关理论,采用傅里叶级数逼近{ui,j}进行空间离散求解.

(3)

(4)

引理1[12]对于任意的网络函数u∈Mh,扩散算子(Δ+1)2u及非局部卷积算子G*u的谱离散形式分别为

1.2 显式稳定性积分因子龙格库塔求解非局部SH方程

相较于传统的强稳定性龙格库塔方法,强稳定性积分因子龙格库塔可避免线性算子的时间步长限制,但由于非线性算子带来的时间步长限制,需要引入一种无时间步长限制的保界格式.

显式稳定性积分因子龙格库塔法(eSIFRK)[13,18-19]是一种显性格式且保极值原理的离散方法,其时间步长的约束仅取决于非线性项,故时间步长大小的选择与空间网格大小无关.

采用显式稳定性积分因子龙格库塔法,分别建立求解式(1)的一步一阶、二步二阶、三步三阶、四步四阶的无时间步长限制的保界格式.

积分因子(IF)法[20]的步骤如下.

首先,将式(1)改写为

ut=Lu+f(u).

(5)

式中：Lu=-(Δ+1)2u;f(u)=εu-uG*u2.

其次,引入新变量v,定义为

v=e-Ltu.

(6)

式(6)中：e-Lt为积分因子.

然后,式(5)两边同时乘以e-Lt,可得

e-Ltut-Le-Ltu=e-Ltf(u).

(7)

注意到vt=e-Ltut-Le-Ltu,则式(7)可简化为

vt=e-Ltf(eLtv).

(8)

根据文献[13],可得式(8)的s步稳定性积分因子龙格库塔格式为

u(0)=un,

(9)

(10)

un+1=u(s).

(11)

给定s=1,2,3,4,可得一步一阶显式稳定性积分因子龙格库塔格式eSIFRK(1,1)为

un+1=eτL[un+τf(un)].

二步二阶显式稳定性积分因子龙格库塔格式eSIFRK(2,2)为

.

三步三阶显式稳定性积分因子龙格库塔格式eSIFRK(3,3)为

四步四阶显式稳定性积分因子龙格库塔格式eSIFRK(4,4)为

2 数值算例

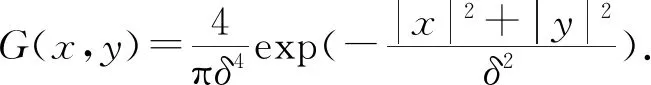
数值解的L2范数误差ErrL2(τ,h)为

数值解的最大误差Errmax(τ,h)为

2.1 算例1

为了验证时间收敛阶,算例1的空间区域Ω=[-20,20]2,初始值为

u0(x,y)=0.01×(cos πx+cos πy+2cos 0.25πy).

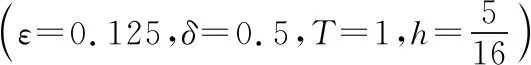
表1 不同时间步长下的时间误差和时间收敛阶Tab.1 Time errors and time convergence rates at different time

由表1可知：时间收敛阶都达到了预期精度.

2.2 算例2

算例2考虑带有随机初始扰动的非局部SH方程,其空间区域Ω=[-64,64]2,初始值为

u0(x,y)=0.07+0.001×rand(x,y).

式中：rand(x,y)表示取值在[-1,1]的随机数.

设置系数ε=0.035,δ=0.5,固定空间步长h=1,时间步长τ=1.

采用四步四阶显式稳定性积分因子龙格库塔格式可得不同时刻数值解图像和能量图(T=2 000),如图1所示.由图1可知：能量是递减的.

(a) T=0 (b) T=300 (c) T=500 (d) T=700

2.3 算例3

为了研究数值解与能量的变化,算例3空间区域Ω=[-64,64]2,初始值为

设置系数ε=0.035,δ=0.5,固定空间步长h=1,时间步长τ=0.1.

采用四步四阶显式稳定性积分因子龙格库塔格式可得不同时刻数值解图像及能量图(T=1 000),如图2所示.由图2可知：能量是递减的.

(a) T=0 (b) T=5 (c) T=20 (d) T=50

2.4 算例4

考虑空间区域Ω=[-150,150]2时液体晶体的生长,初始值为

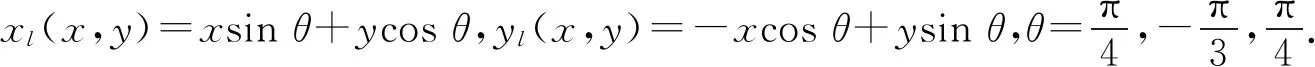
采用四步四阶显式稳定性积分因子龙格库塔格式可得不同时刻数值解图像及能量图(T=1 000),如图3所示.由图3可知：随着时间的推移,微晶相互碰撞并开始形成晶界;当T=1 000时,能量随着时间逐渐减小达到稳态.

(a) T=0 (b) T=50 (c) T=200 (d) T=400

3 结束语

结合积分因子龙格库塔法和傅里叶谱方法求解非局部SH方程,得到一种快速有效的数值格式,数值算例表明文中算法具有较好的稳定性及较高的准确性,且满足能量递减性质.