一类加权序列空间中广义齐次核的Hilbert型离散不等式和序列算子的有界性

张丽娟,洪 勇,,孔荫莹

(1.广州华商学院 数据科学学院,广东 广州 511300;2.广东财经大学 统计与数学学院,广东 广州 510320)

(1)

由于Hilbert不等式在研究算子的有界性及算子范数中有重要应用,因而受到广泛关注。设r>1,φ(m)>0,将lr(N+)推广为加权序列空间:

是以K(m,n)为核的Hilbert型离散不等式。当加权序列空间中的权函数为幂函数时,各国学者已经得到了许多结构优美的Hilbert型不等式。

(2)

文[3]得到:

(3)

式(2)与式(3)的常数因子都是最佳值。

文[4]考虑了抽象的λ阶齐次核,引入搭配参数a,b,首次讨论了Hilbert型离散不等式的最佳参数条件,得到不等式:

(4)

加权序列空间:

1 若干引理

设G(u,v)是λ阶齐次函数,λ1λ2≠0,称K(x,y)=G(eλ1x,eλ2y)为广义齐次函数,显然K(x,y)具有性质:

引理1设g(u)>0,λ>0,c>0,λ0∈R,g(u)分别在(0,c]上递增和在[c,+∞)上递减,则

证明因为g(u)分别在(0,c]上递增和在[c,+∞)上递减,故g(c)是g(t)在是的最大值。

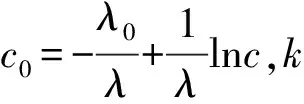
(g(eλk+λ0)(k+1-c0)+g(eλ(k+1)+λ0)(c0-k))≤

g(c)(k+1-c0)+g(c)(c0-k)=

引理2设λ1>0,λ2>0,c1>0,c2>0,G(u,v)是λ阶齐次非负函数,K(x,y)=G(eλ1x,eλ2y),G(1,tλ2)t-bp分别在(0,c1]上递增和在[c1,+∞)上递减,G(tλ1,1)t-aq分别在(0,c2]上递增和在[c2,+∞)上递减,则

(5)

(6)

证明记g(t)=G(1,tλ2)t-bp,因为g(t)分别在(0,c1]上递增和在[c1,+∞)上递减,于是有

故式(5)成立。

类似地,可以证明式(6)成立。

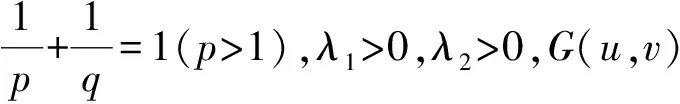
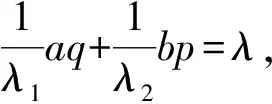
2 加权序列空间中的Hilbert型离散不等式

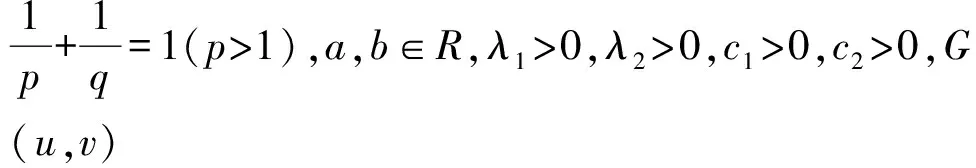
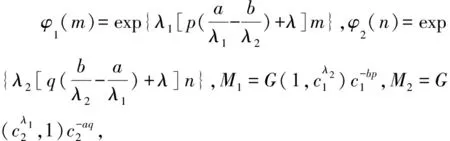
(7)

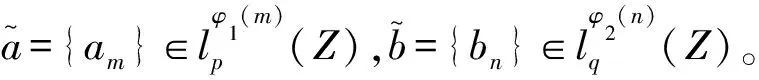
(ⅱ)若λ1=λ2=λ0,aq+bp=λλ0,M1=M2,则

(8)

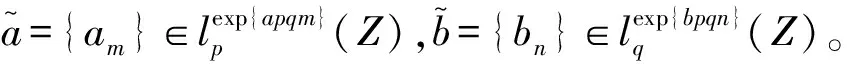
证明(ⅰ)以a,b为搭配参数,根据Hölder不等式及引理2,有

故式(7)成立。

W1(-bp)+M1

从而根据(i),得到式(8)。

3 加权序列空间中离散算子的有界性及算子范数估计

则根据Hilbert型不等式的基本理论,不难证明Hilbert型离散不等式:

(9)

等价于算子不等式:

(10)

根据式(9)与式(10)的等价性和定理1,可得:

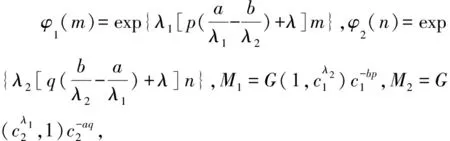
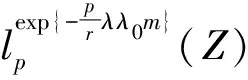
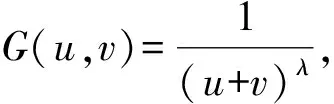
则有

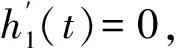
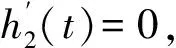
故W1(-bp)<+∞,M1=M2。根据引理3,W2(-aq)=W1(-bp)<+∞。

根据定理2,知推论1成立。

则有

(λλ0-σ)t-λ0]

λλ0)tλ0]

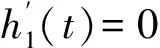
又因为aq+bp=0,由引理3,有W1(-bp)=W2(-aq),而

故W2(-aq)<+∞。同时还有

故M1=M2。

综上,根据定理2,知推论2成立。

注最后,需要指出的是,式(8)中的常数因子W1(-bp)+M1是否是最佳值,不得而知,这是需要进一步研究的问题。