基于β-相似关系的广义多粒度粗糙集模型
2023-10-09刘玉锋孙文鑫
刘玉锋 孙文鑫
1(重庆大学城市科技学院 重庆 402167)
2(重庆水利电力职业技术学院 重庆 402167)
0 引 言
波兰数学家Pawlak[1]提出的粗糙集是一种处理不确定性问题的计算工具。粗糙集理论是建立在等价关系的基础上,通过等价关系把研究对象分成不同的等价类进而进行不确定信息知识的获取和信息挖掘。目前此理论已成功应用到了决策分析、规则提取和过程控制等领域。
经典粗糙集的一个局限性是处理的分类必须是完全正确的,因而其分类结果要求是精确的[2-4]。然而在实际应用中,由于各种原因会造成数据误差的存在,对象和对象之间的不可分辨关系也会存在误差。为了克服局限性,拓宽粗糙集理论的应用,学者们从不同角度对其进行推广,提出了程度粗糙集[5]、变精度粗糙集[6]、相似关系粗糙集等[7]。
基于β-相似关系的粗糙集是一种适应数据误差的粗糙集模型,该模型具有一定的知识容错能力,弥补了等价关系下粗糙集模型的局限性。只要求对象与对象之间大部分信息是相同的,忽略小部分的信息,实现知识的分类,知识分类所需的信息量可以通过相似度水平来控制。
多粒度[8]是由Qian等提出的一种新的数据分析的方法。从粒计算的角度分析单个二元关系(知识粒度)下粗糙集的不足,提出了多个二元关系(知识粒度)下的多粒度粗糙集。Qian等最开始只提出了乐观和悲观多粒度,Xu等[9]提出了一种介于乐观和悲观之间的广义多粒度粗糙集,这种粗糙集是乐观和悲观多粒度的推广模型,也完善了多粒度粗糙集模型。近年来,多粒度粗糙集理论的研究也是硕果累累[8-13]。
本文将结合粒度数选择的不确定性和分类选择的不确定性建立基于β-相似关系的广义多粒度粗糙集。
1 预备知识
为方便本文的论述和有关性质的研究,本节首先给出需要用到的一些基本概念。
定义1[4]称I=(U,A,F)为一个信息系统,其中U为对象集,即U={x1,x2,…,xn}。而A为属性集,即A={a1,a2,…,am}。F={fj:j≤m},其中fj:U→Vj,Vj为属性aj的值域。对于B⊆A,令RB={(xi,xk)∈U2|fl(xi)=fl(xk),∀al∈B},则称RB为信息系统I上的等价关系。令[xi]B={xk∈U|fl(xi)=fl(xj),∀al∈B},则称[xi]B为对象xi关于等价关系RB的等价类。
定义2[8]设I=(U,A,F)为信息系统,对于X⊆U,A1,A2,…,As⊆A,定义:
(1)
(2)
(3)
(4)
定义3[14]设I=(U,A,F)为信息系统,对于X⊆U,P1,P2,…,Pl⊆A,定义:
(5)
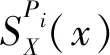
定义4[14]设I=(U,A,F)为信息系统,对于X⊆U,P1,P2,…,Pl⊆A,定义:
(6)
(7)
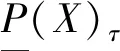
2 基于β-相似关系的多粒度粗糙集
为了扩大粗糙集理论的应用,Qian等[8]把单个二元关系(知识粒度)下粗糙集推广到多个二元关系(知识粒度)下定义的多粒度粗糙集中,本节将多粒度粗糙集推广到β-相似关系上,建立了基于β-相似关系的多粒度粗糙集。

定义5设I=(U,A,F)为信息系统,对于X⊆U,A1,A2,…,As⊆A,参数β∈[0,1],定义:
(8)
(9)
(10)
(11)
性质1设I=(U,A,F)为信息系统,对于X⊆U,A1,A2,…,As⊆A,参数β∈[0,1],有下列性质成立。
(12)
(13)
(14)
(15)
(16)
(17)
(18)
(19)
(20)
(21)
证明式(12)-式(13)对任意的X⊆U,有:

式(14)-式(15)由定义5直接可得。
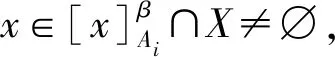
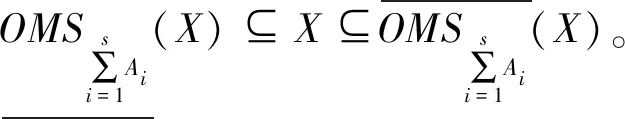
式(17)-式(18)对任意的X⊆U,有:

式(19)-式(20)由定义5直接可得。
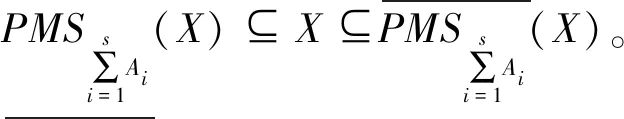
性质2设I=(U,A,F)为信息系统,对于X,Y⊆U,A1,A2,…,As⊆A,参数β∈[0,1],有下列性质成立。

(22)
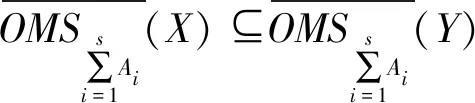
(23)

(24)
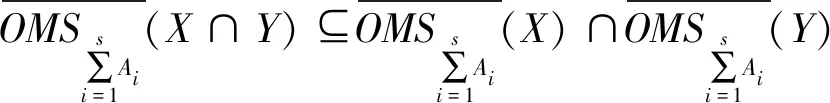
(25)

(26)
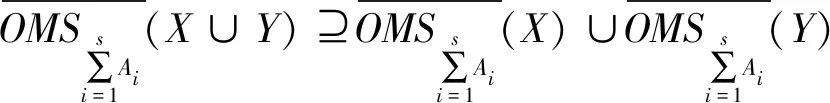
(27)
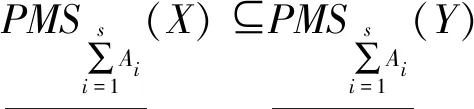
(28)
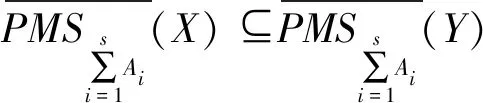
(29)

(30)
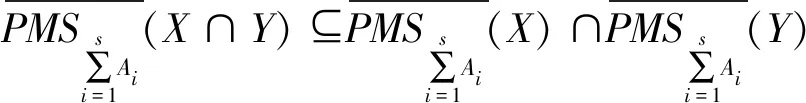
(31)
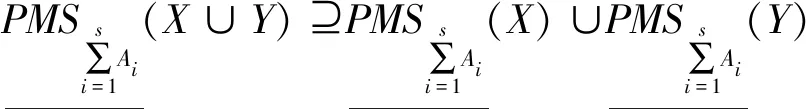
(32)
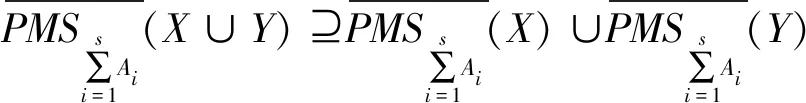
(33)

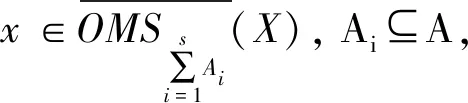
(3)-(6) 由定义5和性质2直接可得。
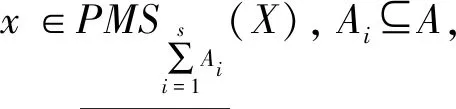
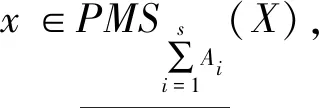
(9)-(12) 由定义5和性质1直接可得。
定理1设I=(U,A,F)为信息系统,对于任意集合X⊆U,A1,A2,…,As⊆A,若β=1,则有:
(34)
(35)
(36)
(37)
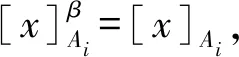
定理1表明:当β=1时,基于β-相似关系的多粒度粗糙集可退化为Qian等[8]定义的多粒度粗糙集。
3 基于β-相似关系的广义多粒度粗糙集
在基于β-相似关系的多粒度粗糙集中,要求满足条件的粒度数量是至少一个和所有的粒度。然而在实际应用问题中要求满足条件的粒度数量可以是其他可能。为了更好地处理不确定知识。本节建立基于β-相似关系的广义多粒度粗糙集,这种粗糙集是基于β-相似关系的多粒度粗糙集的推广模型。
定义6设I=(U,A,F)为信息系统,对于X⊆U,A1,A2,…,As⊆A,定义:
(38)
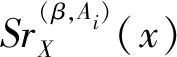
定义7设I=(U,A,F)为信息系统,对于X⊆U,A1,A2,…,As⊆A,参数β∈[0,1],τ∈(0,1],定义:
(39)
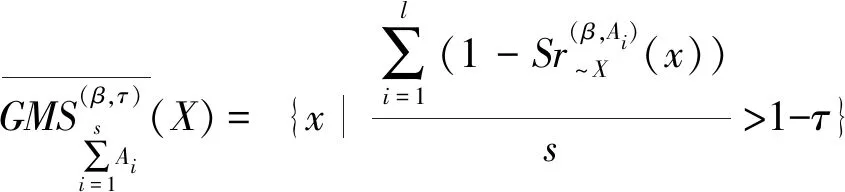
(40)
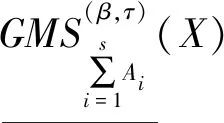
性质3设I=(U,A,F)为信息系统,对于X⊆U,A1,A2,…,As⊆A,参数β∈[0,1],有下列性质成立。
(41)
(42)
(43)
(44)
(45)
证明式(41)-式(42)对任意的X⊆U,有:
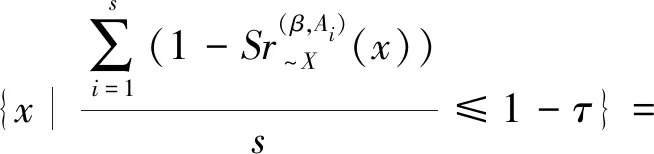
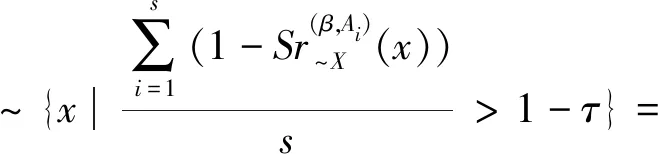

性质4设I=(U,A,F)为信息系统,对于X、Y⊆U,A1,A2,…,As⊆A,参数β∈[0,1],有下列性质成立。

(46)
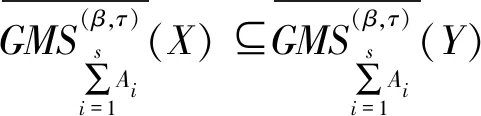
(47)
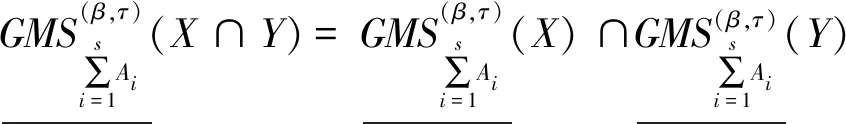
(48)
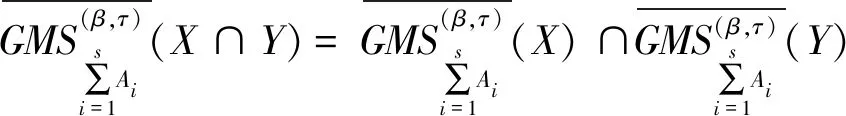
(49)
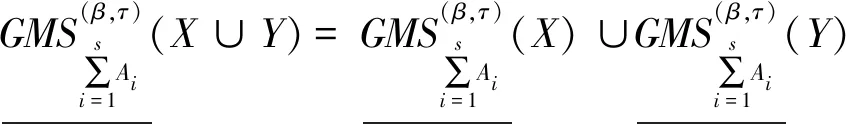
(50)
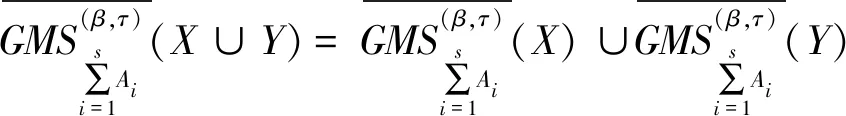
(51)

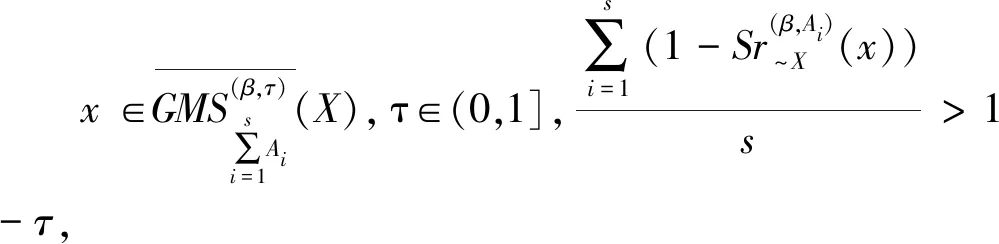
(3)-(6) 由定义6和性质4直接可得。
定理2设I=(U,A,F)为信息系统,对任意的集合X⊆U,A1,A2,…,As⊆A,参数β∈[0,1],τ∈(0,1],则有:
特别地,当τ=1时:
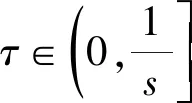
证明根据定义5、定义7直接可得。
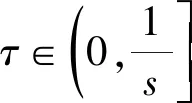
定理3设I=(U,A,F)为信息系统,对任意的集合X⊆U,A1,A2,…,As⊆A,参数τ∈(0,1],α,β∈[0,1]且α<β,则有:
(52)
(53)
证明根据定义5、定义7直接可得。
4 案例分析
近年来全球各种传染疾病不断暴发,如鼠疫、埃博拉、SARS和新型冠状病毒肺炎等疾病通过不同的途径威胁人类生命安全。在传染病暴发的初期,为了控制疫情的扩散,各级政府都会采取紧急控制措施,如何划分已感染人群、可能感染人群和未感染人群成为其关键问题。某传染病感染初期主要有以下9个症状:发热、乏力、干咳、鼻塞、流涕、腹泻、胸闷、呼吸困难和精神弱,记为A={a1,a2,…,a9}。某地区有10人可能感染该传染病病毒,记为U={x1,x2,…,x10},相关症状信息见表1。现将上述9个症状分为3个组(粒度)进行进一步检测。第一组为发热、乏力、干咳症状,记为A1={a1,a2,a3};第二组为鼻塞、流涕和腹泻症状,记为A2={a4,a5,a6};第三组为胸闷、呼吸困难和精神弱症状,记为A3={a7,a8,a9}。经进一步检测,10人中有6人被确诊为病毒感染者,记为X={x1,x2,x3,x4,x6,x7}。
注:“0”表示无症状,“1”表示症状较轻,“2”表示症状较严重。

根据多粒度粗糙集定义可以计算得:
β=1时,由各粒度下等价类和β-相似关系支持特征函数计算得表2。令τ=1,根据基于β-相似关系的广义多粒度粗糙集定义可以计算得:
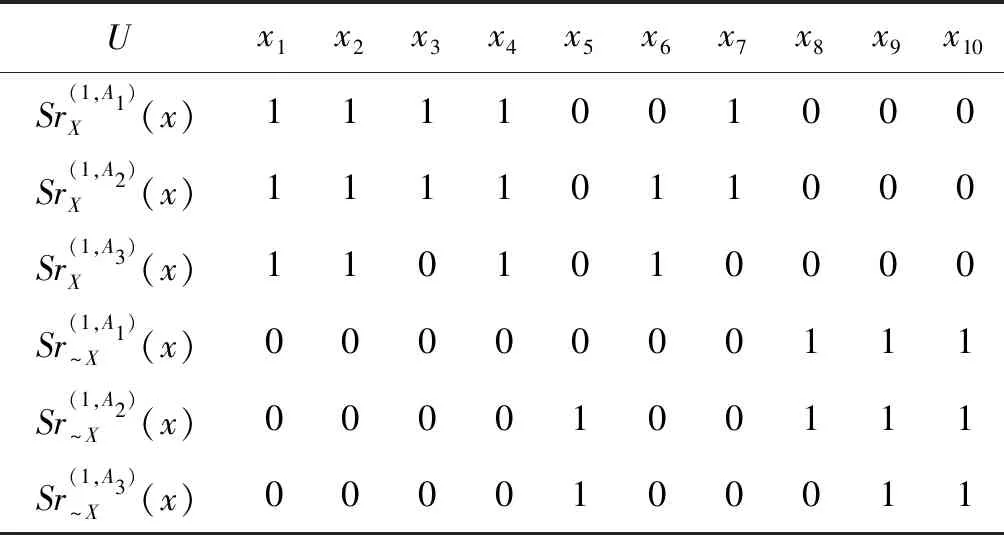
表2 β=1时的β-相似关系支持特征函数值表
令τ=0.65,根据基于β-相似关系的广义多粒度粗糙集定义可以计算得:
令τ=0.3,根据基于β-相似关系的广义多粒度粗糙集定义可以计算得:
β=0.65时,由表1可计算得各粒度下β-相似类:
根据基于β-相似关系的多粒度粗糙集定义可以计算得:
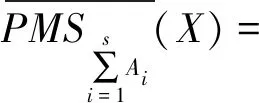
β=0.65时,由各粒度下β-相似类和β-相似关系支持特征函数计算得表3。令τ=1,根据基于β-相似关系的广义多粒度粗糙集定义可以计算得:
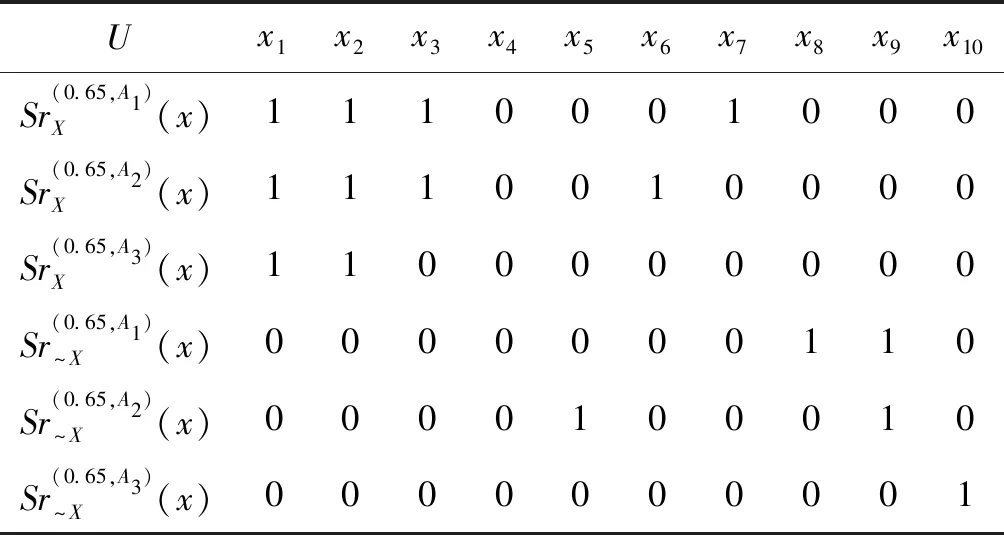
表3 β=0.65时的β-相似关系支持特征函数值表
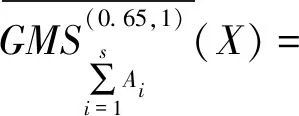
令τ=0.65,根据基于β-相似关系的广义多粒度粗糙集定义可以计算得:

令τ=0.3,根据基于β-相似关系的广义多粒度粗糙集定义可以计算得:
显然:
这个结果验证了定理1、定理2和定理3的正确性。
由上述结果可知,下近似随着β减小而减小,上近似随着β减小而增大,即随着要求满足条件的粒度数越少下近似越小,上近似越大。在实际应用中应该根据医务人员(专家)对传染病的了解而设置合适的β值(选择合适的粒度数),以防止因分类隔离不当,从而扩大传染病传播。因此,基于β-相似关系的广义多粒度粗糙集模型的数据分析方法更具有实际意义,它在决策过程中能够一定程度上解决因粒度选择不当可能带来的决策失误。
5 结 语
本文从粒度数选择和分类选择的角度提出基于β-相似关系的乐观多粒度、悲观多粒度粗糙集模型,进一步提出基于β-相似关系的广义多粒度粗糙集模型,并讨论了本文模型与其他多粒度粗糙集之间的关系,丰富和完善了多粒度粗糙集理论。实例分析验证了相关定理,进一步表明了本文模型改善了多粒度粗糙集模型在决策分析中的局限性。本文模型通过控制参数β和τ来选择合适的粒度数和分类,使决策分析更加准确。未来还需进一步探索本文模型中决策规则提取和约简方法。
