改进并行蚁群算法在配电网网架优化中的应用
2023-10-09卜冠南刘建华张冬阳胡任远罗逸轩
卜冠南 刘建华 张冬阳 胡任远 罗逸轩
(福建工程学院计算机科学与数学学院 福建 福州 350118)
(福建省大数据挖掘与应用技术重点实验室 福建 福州 350118)
0 引 言
配电网网架优化是一个复杂的非线性组合优化问题,网络中拥有大量的线路和负荷点,主要内容是找到一种使配电网络建设的投资和运行费用最小的线路规划方案,且同时需要满足相关约束条件。常规数学优化算法虽然在理论上可以求得最优解,但实际上随着配电网网架问题的规模与复杂度的不断增大时,常规数学优化算法很难有效地解决问题,因此以往学者将智能算法应用到配电网规划问题中,如禁忌搜索算法[2]、模拟退火算法[3-4]、粒子群算法[5-7]、遗传算法[8-9]、差分进化算法[10]、免疫二进制萤火虫算法[11]等。但是这些算法也有一些不足,就是在求解大规模的配电网络系统时,往往无法实现对整个解空间的完全搜索,难以求得最优解。而蚁群算法[12]具有信息正反馈和启发式搜索的特点,对求解组合优化问题有很好的适用性,但传统蚁群算法有收敛速度慢、易陷入局部最优的不足。因此本文在并行蚁群算法[13]的基础上,通过改进蚁群组间信息沟通方式及分组策略,提高了算法收敛性,增强了算法的全局搜索能力。文中将改进算法应用到配电网优化问题具体案例,实验结果表明此改进算法相较于传统蚁群算法和并行蚁群算法有更好的寻优能力。
1 配电网网架优化的数学模型
配电网网架优化的目标是使配电网架建设费用和电能损失费用最小,同时满足线路允许通过的最大电流、电压上下限约束,辐射性和连通性网架结构。
优化目标函数为:
C1×|ΔI|+C2×|ΔU|
(1)
式中:γi为资本回收率;∂i为年设备维修率;X=(x1,x2,…,xi),xi∈(0,1);ai为支路i单位长度投资费用;li为支路i的线路长度;C0为电价;τmax为系统最大负荷损耗时间;ΔPi为支路i的功率损耗;C1为支路过流惩罚系数;ΔI是支路电流超限的数值;C2为节点电压越限的惩罚系数;ΔU为电压超限的数值。
约束条件为:
① 支路电流约束:
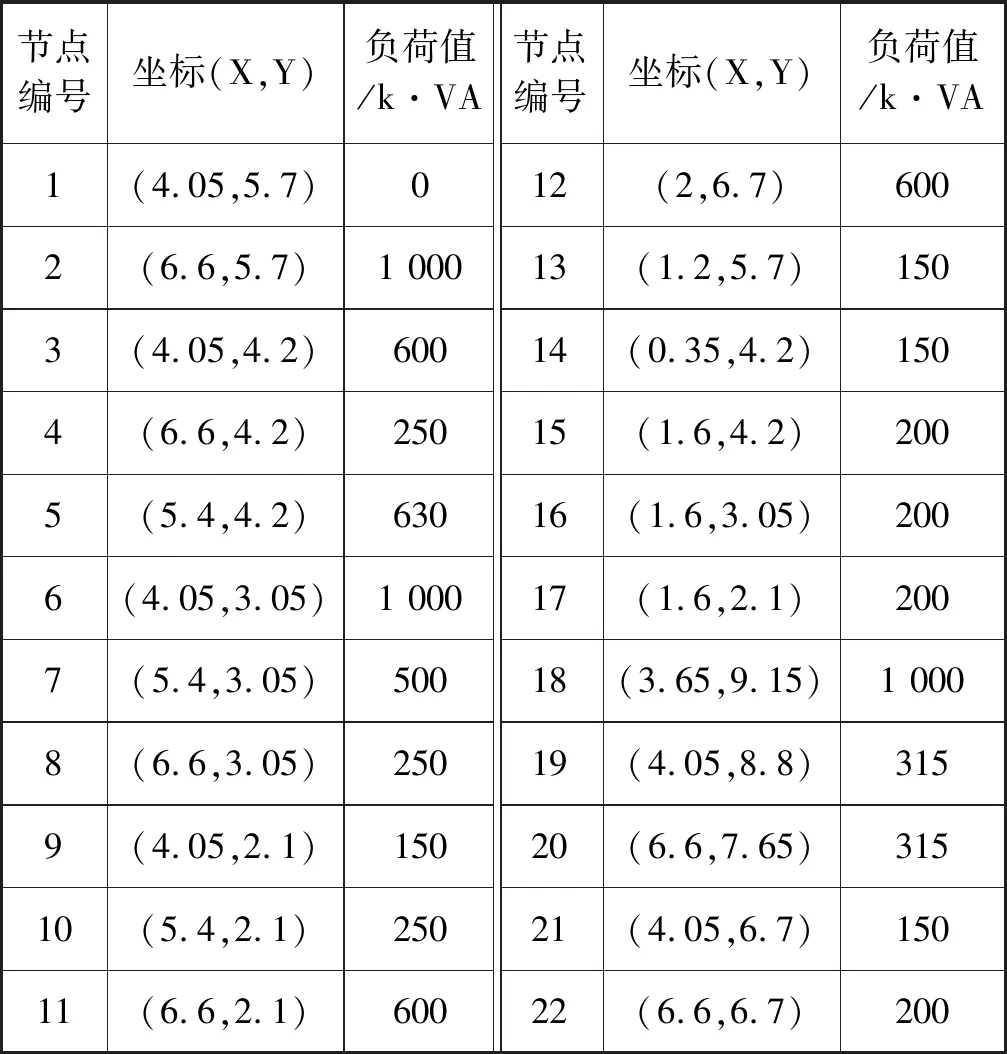
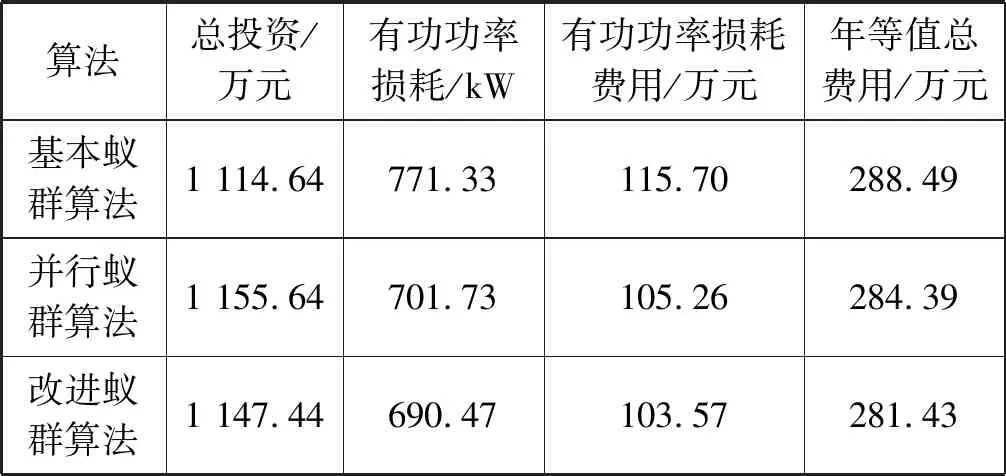
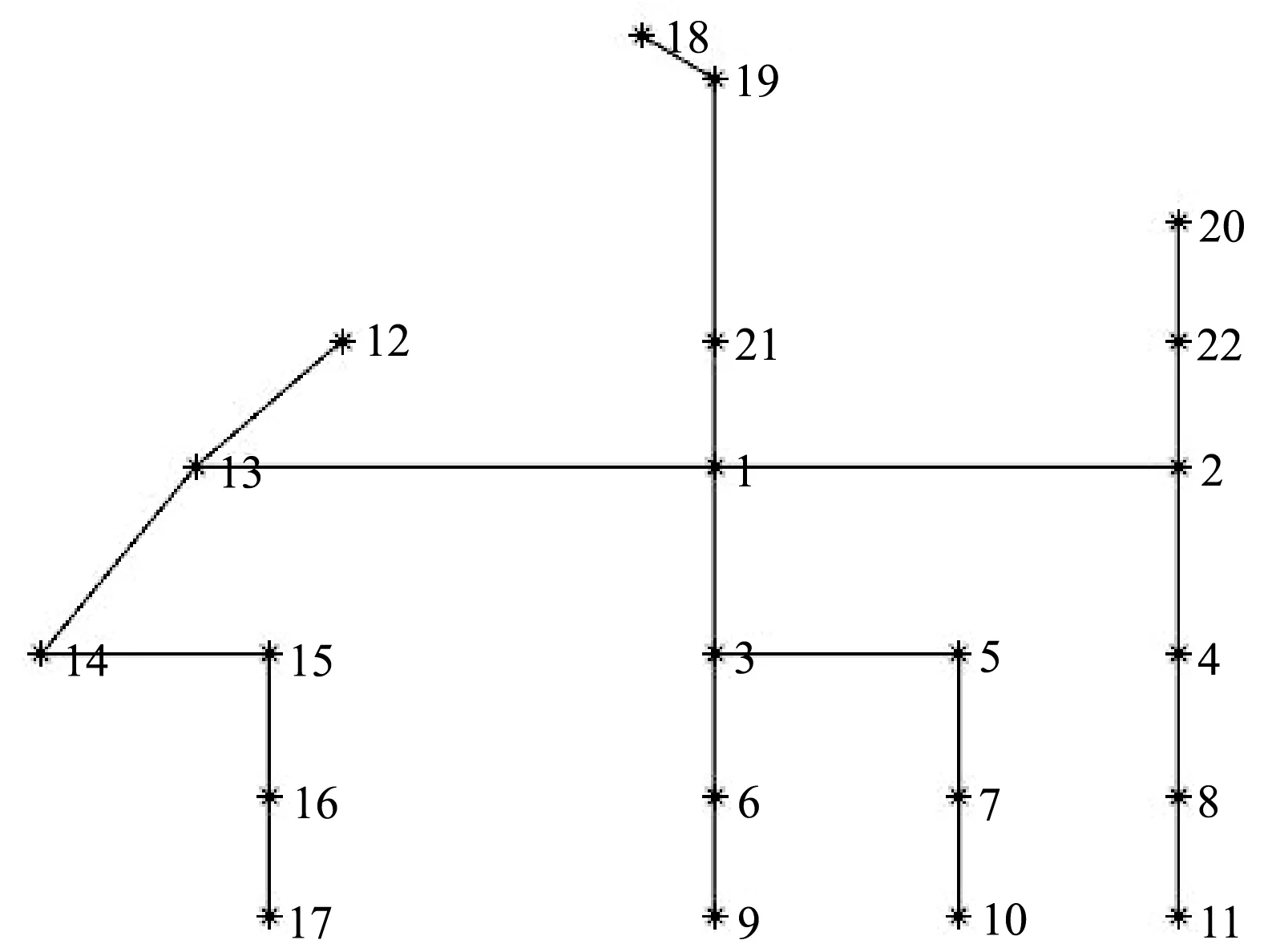
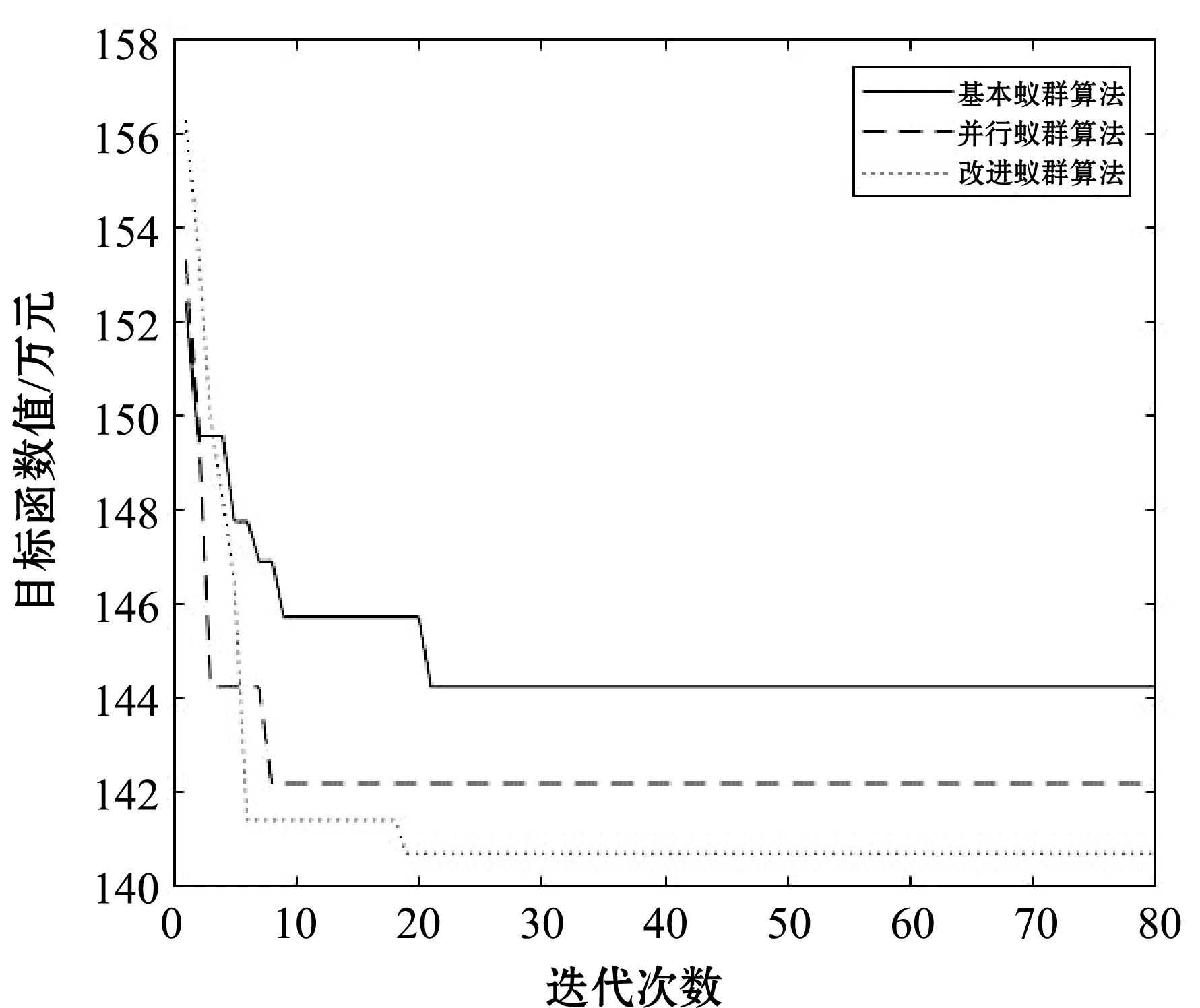
Ii (2) 式中:Ii为支路i流过的电流;Iimax为支路i允许流过的最大电流。 ② 负荷点电压约束: Umin (3) 式中:Um为节点m的电压;Umax、Umin分别为负荷节点的电压的上下限。 ③ 网架辐射性约束,即电源点与任意负荷节点之间的路径唯一。 ④ 网架连通性约束,即任意两个负荷或电源节点之间都连通。 蚁群算法,又称蚂蚁算法,最早是由Dorigo等学者提出的,是一种基于群体的模拟进化算法,其灵感来源于蚂蚁在寻找食物过程中发现路径的行为。蚂蚁在运动过程中,会留下一种称为信息素的东西,而蚂蚁自身会根据信息素去选择方向,当然路径信息素越浓,被选择的概率也就越大。蚂蚁根据由信息素强度和路径启发函数决定的状态转移概率选择下一步所要走的路径。蚂蚁经过多次循环迭代寻找最短路线在较短路线上的信息素量增多,较长路径上的信息素量减少,最终最短路径上的信息素量最短。最终蚂蚁根据路径上信息素的量全部倾向于选择最短路径,从而蚂蚁算法找到最优解。 Chu等[13]在Dorigo等的基础上提出了并行蚁群系统(Parallel ant Colony System,PACS),该并行算法将蚂蚁分成若干组,每组蚂蚁独立按照传统蚁群算法搜索可行解。蚂蚁在搜索过程中,每搜索一定的迭代次数后,所有蚂蚁通过组间的信息沟通更新路径信息素。 在PACS中,将所有蚂蚁分为若干组,第g(g=1,2,…,G)组的蚂蚁第k(k=1,2,…,m)只蚂蚁在当前位置i处,按照伪随机比例规则来选择下一个访问的城市j,其表达式如下: (4) 式中:q是区间[0,1]上的一个随机变量;q0是一个[0,1]范围之间的常数;τg(i,j)是第g组的蚂蚁的路径信息素;η(i,j)为启发函数,是i城市与j城市之间的欧氏距离的倒数;J是根据式(5)的路径转移概率公式产生的一个变量。 (5) 式中:α为信息启发因子;β为期望启发因子;allowk为蚂蚁尚未访问过的城市。 当第g组的第k只蚂蚁完成一次旅程后,根据局部信息素更新规则更新每组蚂蚁的路径信息素,更新规则如下: τg(i,j)=(1-σ)×τg(i,j)+σ×τ0 (6) 式中:τ0是一个很小的正常数,σ是信息素挥发因子,0<σ<1。 当每组中的所有蚂蚁都已经完成一次旅程后,根据全局信息素更新规则更新每组蚂蚁的路径信息素,更新规则如下: τg(i,j)=(1-ρ)×τg(i,j)+ρ×Δτg(i,j) (7) (8) 式中:ρ是信息素挥发因子;Q是常数;Lg是第g组的最优路径长度;Rgbest为第g组的最优路径。 随着算法迭代,当算法运行R次后,各组蚂蚁相互之间信息沟通交流,根据图1所示沟通方式更新每组蚂蚁的路径信息素。 更新规则如下: τg(i,j)=τg(i,j)+ε×Δτbest(i,j) (9) (10) 式中:ε是信息素挥发系数;Lg,b是所有组中蚂蚁的最优路径长度。 针对蚁群算法收敛速度慢以及容易陷入局部最优的缺点。文中基于PACS提出两个改进策略: 1) PACS中将蚂蚁分为若干组,增强了全局搜索能力,提高了蚁群算法求解性能。但对于并行蚁群算法,蚂蚁分组并不是越多越好[14],PACS中每组蚂蚁的求解原理还是按照基本蚁群算法的思想在运行,故分组过多,因蚂蚁总数是固定的,这样就导致每组中的蚂蚁过少,算法性能会受到影响,使算法收敛速度降低,全局搜索能力下降;如果增加蚂蚁数量,则会导致算法的时间复杂度增大,降低算法的求解速度。因此本文提出了一种自适应分组策略,即采用一种随迭代分组数自适应减少的方法。在算法前期分组多,增强全局搜索能力且加快算法收敛速度,算法后期分组少,增强局部搜索能力。因此本文将算法迭代周期分为若干段,分组规则如下: (11) 式中:μ表示自适应分组算子;G表示算法最大分组数;t表示当前迭代次数;g(t)表示当前迭代次数为t时,蚂蚁的分组数;Tmax表示最大迭代次数。 自适应分组的策略方法是算法前期分组多,后期分组少。组数减少时,为了保证算法的时间复杂度不变,消失的蚂蚁需要和留存的蚂蚁合并为一组,因此各组蚂蚁的路径信息素要合并融合。融合规则如下: (12) 2) 针对PACS组间蚂蚁沟通交流过程,用所有组最短路径距离进行路径信息素更新,文中提出一种环形结构的沟通方式,如图2所示。将不同组的蚂蚁连接成一个环形结构,蚂蚁搜索迭代R次时,环形结构中的相邻组蚂蚁进行信息沟通,比较蚂蚁所找到的最佳路径,从而进行路径信息素更新。此种方式尽可能地保留了每组蚂蚁的信息,降低了算法陷入局部最优的风险。 图2 根据环形结构更新信息素 信息素更新规则就是将式(10)转换为: (13) 式中:Lg,b是相邻组中蚂蚁的最短路径距离。即组4的路径信息素,由组4蚂蚁和组3蚂蚁沟通后即比较路径长短后确定;组3的路径信息素,由组3蚂蚁和组2蚂蚁沟通后确定,其他组同理。 在算法求解过程中,为了避免蚂蚁在搜索规划方案时形成过多的非辐射状的解,提高算法的搜索效率,减少修复非辐射形解的时间,进而减少计算时间,应尽量使每一只蚂蚁的规划方案限制为辐射状网络结构方案。Vkt为连入树的节点集合,Ukt为未连入树的节点集合,Ekt为当前可建线路的集合,Enew为蚂蚁搜索过的路线集合,第k只蚂蚁每一次游程时,先以Pk(i,j)从Ekt中选择一个边,将选择的边放到Enew中,然后更新Vkt、Ukt、Ekt集合里的元素,重复上述步骤,直到Ukt集合为空,Enew中的边就是第k只蚂蚁的路线规划方案。 算法求解过程中,使用前推回代法计算蚂蚁搜索得到的网络规划方案中的潮流参数,进而使用式(1)中配电网网架优化目标函数f(X)评价每只蚂蚁的规划方案的好坏,改进蚁群算法流程如图3所示。 图3 算法流程 本文采用文献[15]中的算例,表1为各负荷节点的大小及坐标,坐标单位为cm,与真实街道的比例尺是1∶20 000,该配电网网架结构为中国北方某城市一区域的实际街道图,该区域有33条街道、21个负荷点,节点1为变电站位置,如图4所示。 表1 节点负荷数据 图4 城市街道图 用MATLAB 2018软件编写程序,蚁群算法中:α=1;β=2;σ=0.1;ρ=0.1;ε=0.1;Tmax=80;Q=1; 蚂蚁总数为16;最大分组数G=8。目标函数中参数设置为:电价C0=0.5元/(kW·h),惩罚系数C1=C2=1 000;年等值系数γi+∂i=0.155,系统年等效损耗小时数τmax=3 000 h。线路单位投资费用为20.5万元/km,导线选用LGJ50。通过基于自适应分组策略的改进蚁群算法生成的网架优化结果如图5所示。该算例很好地验证了改进算法在网架优化中的可行性。为验证本文算法的优劣性,采用并行蚁群算法和基本蚁群算法分别对算例进行分析计算,将所得结果与上述结果进行对比,收敛曲线如图6所示,对比结果如表2所示。 表2 优化结果比较 图5 优化后网架结构图 图6 目标函数收敛曲线 从图6的目标函数曲线走势可以看出,改进蚁群算法在三种算法求解中求得的解是最优的,且改进算法求解算例相较于基本蚁群算法和并行蚁群算法有更快的收敛速度。从表2中可以看出,改进蚁群算法的各项指标都要好于并行蚁群算法,且与基本蚁群算法相比,虽然线路总投资费用较高,但是功率损耗费用低。综合看来,本文改进算法是更优的,验证了改进算法求解网架优化问题上的可行性和有效性。 本文以系统年综合费用作为目标函数,采用自适应分组策略的改进并行蚁群算法,对并行蚁群算法中的蚂蚁进行自适应分组,且提出一种新的蚂蚁组间信息沟通方式,克服了蚁群算法易陷入局部最优解的缺点,一定程度上加快了算法的收敛速度,使得其寻优性能有了显著的提高。通过具体实例的实验结果验证了改进蚁群算法在可行性和有效性。2 自适应分组的并行蚁群算法
2.1 蚁群算法分析
2.2 并行蚁群算法原理
2.3 改进并行蚁群算法

3 改进蚁群算法求解配电网网架优化
3.1 生成树方法构造配电网网络结构
3.2 改进算法求解配电网架优化步骤
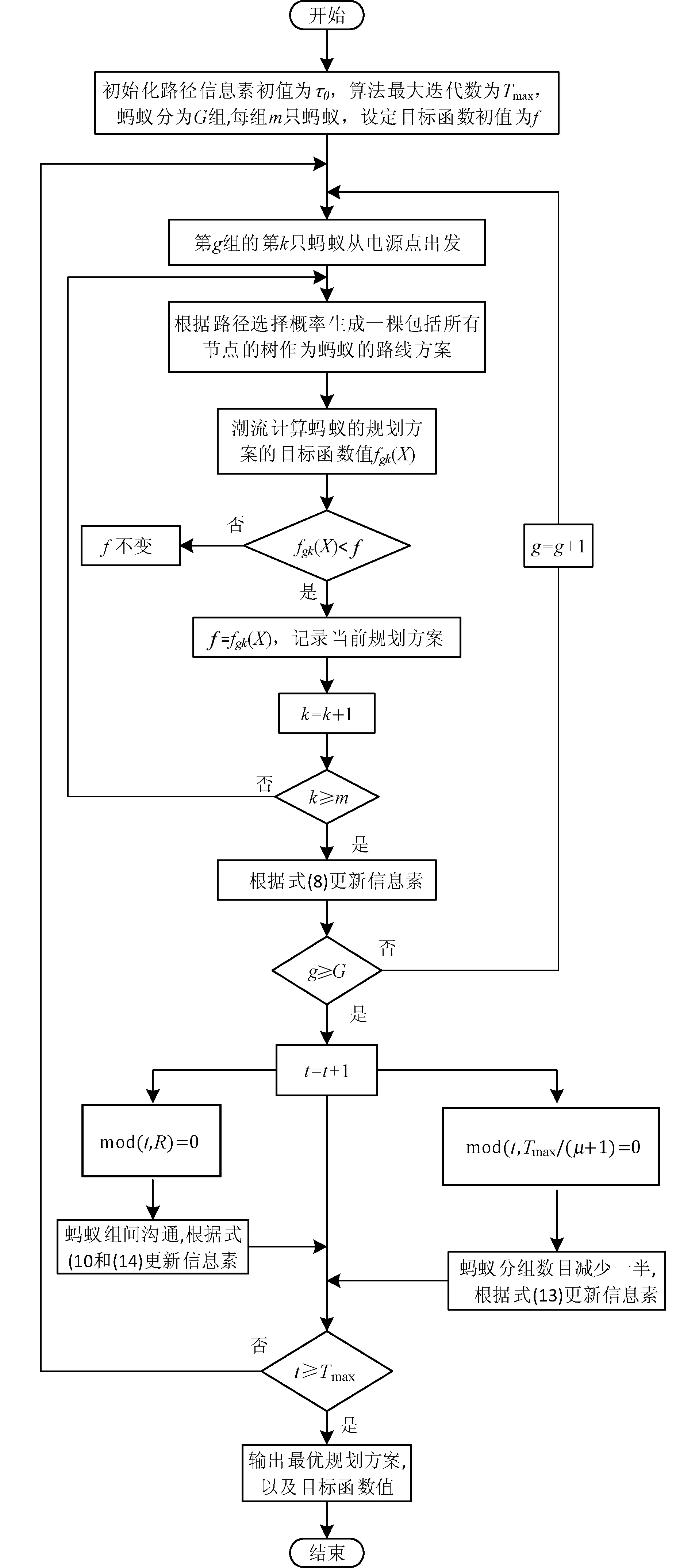
4 算例分析

5 结 语
