纵断面曲率检测及线形识别方法

程朝阳 王昊 李颖 余宁 魏世斌 韩志

中国铁道科学研究院集团有限公司 基础设施检测研究所， 北京 100081

竖曲线可以缓和线路纵断面上坡度的突然变化，改善变坡点的竖向舒适度，是轨道交通线路纵断面设计中的重要参数。为了方便测设及养护维修，国内竖曲线一般采用圆曲线。评价圆形竖曲线的参数主要有半径和长度，其中半径需综合考虑旅客舒适性、车轮不脱轨、列车不脱钩不断钩、养护维修等要求。竖曲线可以改善变坡点的变化，但列车通过竖曲线区段时仍会引起车辆的垂向增减载，同时会引起各种振动的叠加，尤其是在竖曲线起点处，轮轨垂向作用力以及车体垂向加速度［1］都会达到最大值，增大了列车倾覆的可能性，增加了轮轨磨耗。

纵断面设计线形包括直线和竖曲线，如图1所示。其中，PBP为变坡点；PZY、PYZ为直圆段、圆缓段的桩点；T为桩点到变坡点的距离；i1和i2为相邻直线坡段的坡度；α1为坡度角。文献［2］进行了竖曲线参数分析和动力学分析，得出纵坡坡度对纵断面线路参数影响不大。文献［3］研究表明，竖曲线各参数对纵断面线形平顺性的主要影响位置为竖曲线的直圆点和圆直点，且不同参数对平顺性的影响不同。

本文针对纵断面设计线形中影响较大的竖曲线的曲线半径，设计一种对应的纵断面曲率检测算法；基于竖曲线的曲率检测结果，提出一种纵断面线形识别算法；基于联调联试综合检测列车的实测数据，对比分析纵断面曲率检测算法、纵断面线形识别算法的计算结果与线路纵断面台账信息。

1 纵断面曲率检测算法

如图2 所示，建立惯性坐标系O-xbybzb。其中，坐标原点为三轴陀螺仪敏感轴交汇的中心点O；yb轴正向为轨道延伸方向；xb轴正向为轨道平面内沿轨道延伸的方向垂直向右；zb轴垂直于xb轴和yb轴，并构成右手直角坐标系。陀螺仪滚动角速率、点头角速率和摇头角速率分别绕xb、yb和zb转动。该坐标系中，竖曲线方向与点头陀螺仪敏感轴方向一致，故点头陀螺仪为竖曲线线形检测的主传感器。

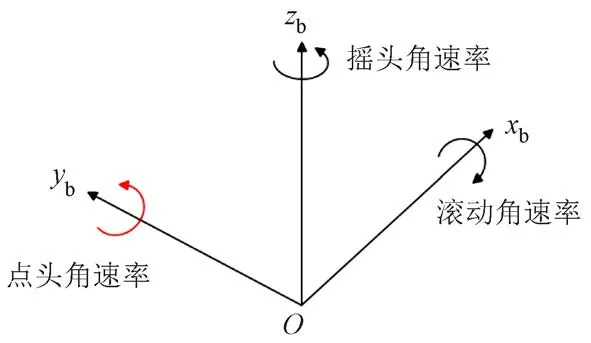
图2 高速铁路纵断面检测坐标系

坐标系O-xbybzb中，竖曲线正投影方向与点头陀螺仪及yb轴加速度计的敏感轴方向重合。当惯性坐标系同时存在摇头角速率和滚动角速率时，点头角速率存在微小修正，此时竖曲线曲率（Cv）表达式为

式中：ωpitch、ωroll、ωyaw分别为陀螺仪的点头角速率、滚动角速率、摇头角速率；t为采样时间间隔。

式（1）第2项表示当存在侧滚角速率时，摇头角速率在点头角速率敏感轴方向的分量。

为了适应现场要求，竖曲线曲率检测结果需要按照等空间间隔输出。因此，要对包括主分量点头角速率在内的所有传感器分量进行空间采样。采样过程中为了抑制空间频率混叠，首先对点头角速率和摇头角速率进行时间抗混滤波处理，然后对处理后的数据进行空间采样。由于等间隔空间采样时间与速度相关，所以要对空间采样后的数据进行速度补偿［4］，消除速度对抗混滤波器截止频率的影响。空间采样间隔一般为0.25 m，需要对光电编码器信号进行计数。该传感器受到干扰后会有误差和跳变，考虑检测速度不可能发生突变的客观事实，基于卡尔曼最优化递归处理算法对突变速度进行最优估计。竖曲线检测算法具体流程见图3。处理后的信号通过低通滤波器［D（z）］后，即可得到竖曲线曲率。

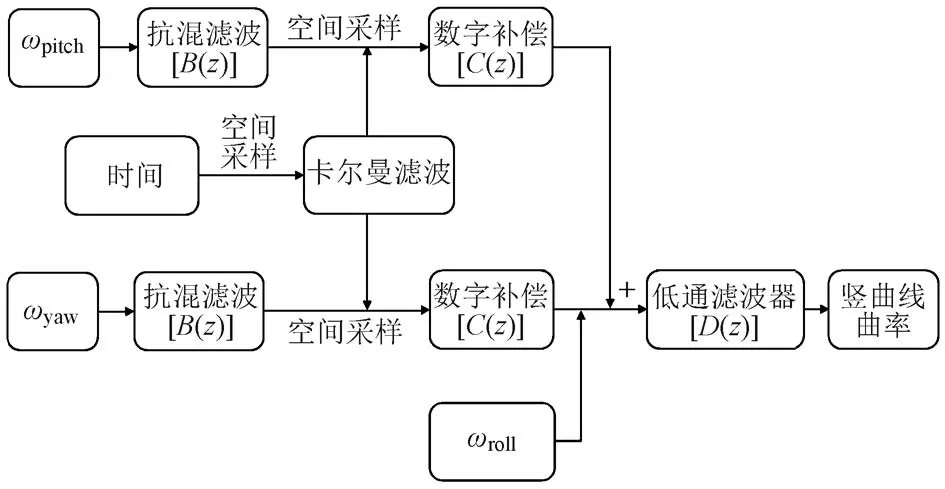
图3 竖曲线检测算法流程

为了适应竖曲线空间频率的实际分布，同时抑制空间采样信号混叠的影响，设计抗混滤波器［B（z）］。表达式见式（2）。对陀螺仪时间序列信号进行抗混滤波处理，其幅频、相频特性曲线见图4。

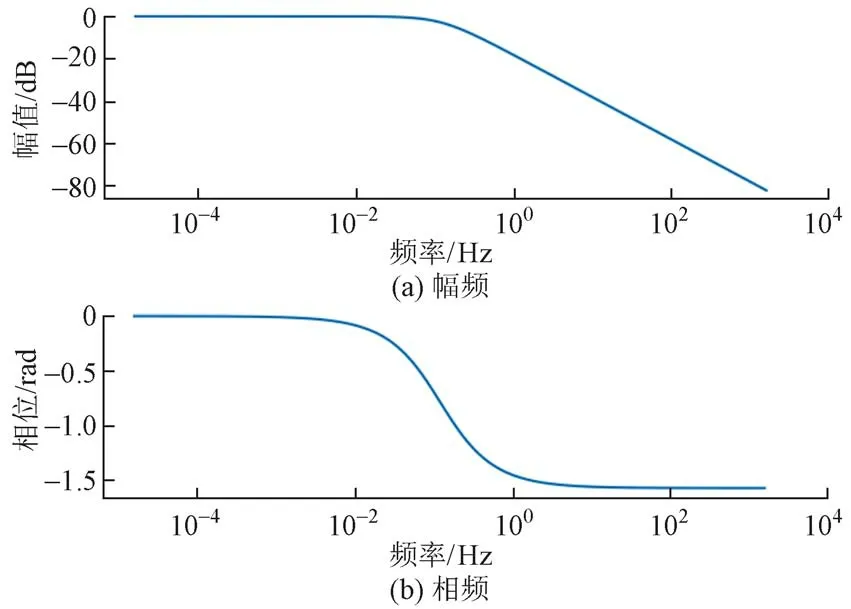
图4 抗混滤波器幅频相频特性

式中：Ω1为常系数；f为传感器频率；z为复变量。

列车的行驶速度时刻变化，因此采用截止频率与速度相关的数字补偿滤波器［C(z)］来消除速度变化和空间采样造成抗混滤波器截止频率变化的影响。C(z)表达式见式（3）。其幅频、相频特性曲线见图5。

图5 数字补偿滤波器幅频相频特性

式中：Ti为时间间隔。

采用矩形窗级联的方式，设计FIR（Finite Impulse Respond Filter）低通滤波器［D(z)］。因FIR 滤波器为线形相位，群延迟为0，所以竖曲线曲率不发生畸变。D（z）表达式见式（4）。其幅频特性见图6。

图6 FIR低通滤波器幅频特性

式中：m、n、p、q均为常系数。

2 纵断面线形识别算法

线形识别是针对纵断面的线形按照特征进行分段。常用的线形特征参数有三种，分别是曲率、正矢和相邻弦的坡度差。选择不同的特征参数对线形进行分段，是因为特征参数的变化趋势不同，分段的效果也不相同。正矢和相邻弦的坡度差这两个特征参数在采样点间隔较小时变化不明显，虽然随着采样点间隔不断扩大，其效果会有所提升，但识别的分段点精度也会降低。因此，选用曲率作为识别纵断面线形的特征参数。

采用曲率作为纵断面线形特征识别参数时，需要按照曲率特征对纵断面曲率检测数据进行分段。数字折线提取转折点时，所采用的经典方法是Douglas-Pucker 算法［5］。该方法简单高效，只需要找一次距离最大值就可得到近似结果，但当测点存在误差时得到的转折点精度较低，且实际测试过程中会出现错误判别。

由于纵断面由直线和圆曲线构成，在忽略检测噪声［6］和轨道变形的情况下，直线坡段的曲率为0，圆曲线的曲率为半径的倒数（恒定常数），故纵断面的曲率波形均由线性元素构成。采用线性拟合的方式对曲率波形进行分段，具体算法如下。

1）按照滑动阈值判断的方式，对曲率波形进行划分，筛选出竖曲线区段。设置阈值，对于大于阈值的数据认为是曲线段，同时设置曲率波形的最小长度和最小幅值，对曲率波形进行筛选。

2）将筛选出的竖曲线区段划分3 个区间，第一段为前坡度直线，第二段为竖曲线区段，第三段为后坡度直线。筛选原则：最大值为圆曲线水平直线的截距，最大值之前的数据属于前坡度过渡段，最大值之后的数据属于后坡度过渡段。

3）纵断面的竖曲线范围内按照y=c进行水平直线回归分析（c为竖曲线范围内的最大值），竖曲线与前后坡度直线过渡段按照y=kx+b进行倾斜直线回归分析（k、b分别为倾斜直线的斜率和截距）。

4）计算水平直线y=c和两条倾斜直线y=kx+b的交点，该交点即为竖曲线的起终点。

5）以竖曲线的起终点为边界，重新划分筛选出的竖曲线区段，重复上述拟合划分过程，直至区间划分的数据不发生变化。

按照上述方法得出的纵断面线形识别算法效果见图7。可知，该方法可以对纵断面的竖曲线及前后的坡度直线进行有效识别。

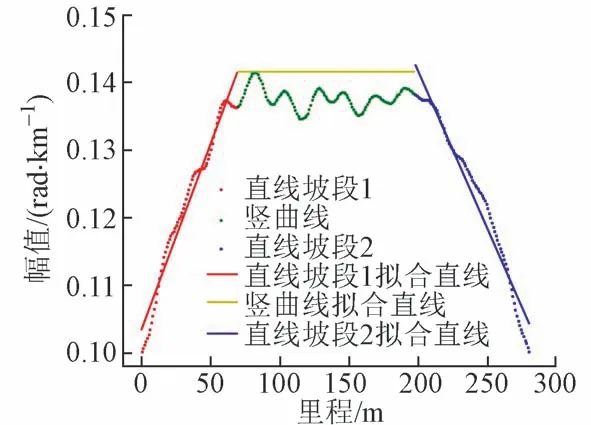
图7 纵断面线形识别算法示例

3 试验验证

利用一高速铁路线路联调联试时高速综合检测列车实测的三轴陀螺仪数据和线路高程的台账数据，对模型和方法进行验证。基于纵断面曲率检测算法的检测结果见图8（a）。高速铁路线路的竖曲线的半径较大，一般为15、25、30 km，曲线长几十米到几百米不等。由于高速综合检测列车点头陀螺安装平面和摇头陀螺安装平面非同一平面，二者之间存在二系弹簧，检测结果存在误差。为验证纵断面竖曲线检测的正确性，选取基线位于零线的竖曲线计算曲线半径和曲线长度［图8（b）］。台账曲线半径为25 km，曲线长度为100 m；检测得到的曲率为0.04 rad/km，曲线长度为112 m，检测结果与台账数据基本相符。

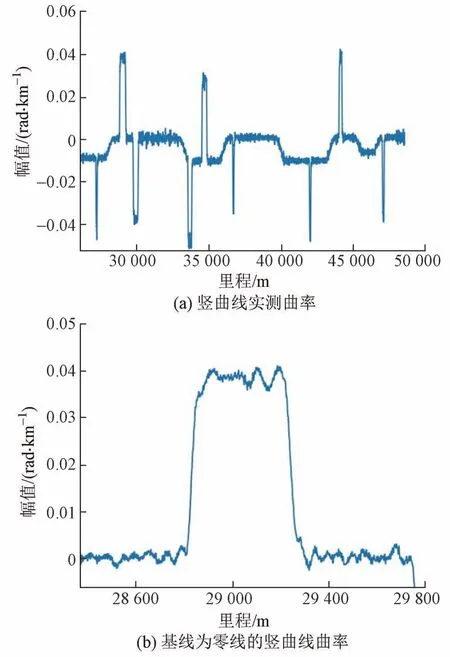
图8 纵断面曲率检测

基于纵断面线形识别算法的纵断面线形识别效果如图9 所示。可见，通过线性拟合的思想可以识别不同长度的竖曲线，将竖曲线和竖曲线前后的直线段分隔开，完成竖曲线线形识别。

图9 纵断面线形识别

4 结语

本文针对纵断面中对列车平稳性影响较大的竖曲线，提出了一种纵断面竖曲线曲率检测算法，可以完成纵断面竖曲线曲率实时检测，检测结果与线路台账吻合性较高。选用纵断面竖曲线曲率实时检测结果作为识别纵断面线形的特征参数，并采用线性拟合的方式对纵断面曲率检测数据进行分段，提出了纵断面线形识别算法，可以完成纵断面的竖曲线及前后的坡度直线的有效识别。