恒定水流下单桩局部冲刷影响因素模拟分析
2023-10-09向琪芪王顺意郭辉裘放
向琪芪 王顺意 郭辉 裘放
1.中国铁道科学研究院集团有限公司 铁道建筑研究所, 北京 100081; 2.中国铁道科学研究院集团有限公司 高速铁路轨道系统全国重点实验室, 北京 100081; 3.中国科学院 力学研究所, 北京 100190; 4.西南交通大学 土木工程学院, 成都 610031
桩基础是海上石油平台、铁路与公路桥梁、海上风机等常用的基础之一。单桩周围水流的剧烈变化会导致局部泥沙输送能力增强,床面附近剪应力增加,引起局部冲刷,从而降低基础承载力,增加基础失稳破坏的概率。单桩基础冲刷是造成结构功能失效、丧失安全性能的主要原因之一。随着近年来气候条件的变化,极端洪水作用时有发生,掌握桩基冲刷机理,采取经济合理的冲刷防护措施至关重要。
单桩基础周围的局部冲刷是非常复杂的水泥和泥沙的运动过程。影响因素有水力因素、泥沙及河床边界因素、结构因素[1-2]。现有研究多采用水槽试验对局部冲刷影响因素开展研究,受试验条件限制,在试验中开展参数化研究比较昂贵且困难。目前计算流体力学(Computational Fluid Dynamics,CFD)软件是相关研究进行数值模拟时常采用的方法。使用CFD 软件可完成很多水槽试验难以开展的工作,如对冲刷过程中流场形态进行观测,提取更为丰富的数值结果,对局部冲刷机理进行解释[3-4]。
本文使用CFD 软件建立水流-单桩-泥沙相互作用的数值模型,以RANS方程作为控制方程,在验证模型桩周流场和冲刷深度准确可靠的基础上,对水流作用下单桩基础局部冲刷过程进行数值模拟,研究不同水流、泥沙参数和结构尺寸对单桩基础局部冲刷的影响规律。
1 数值计算理论基础
1.1 控制方程与湍流模型
假设水流是一种不可压缩黏性流体,满足流体运动的基本控制方程。以RANS方程作为控制方程,引入体积分数和面积分数,其连续性方程及动量守恒方程分别为[5]
式中:i、j= 1, 2, 3 时,xi和xj分别为x、y、z轴坐标;ui和uj为x、y、z轴坐标各方向的速度分量;Ai为各方向的可流动流体面积分数;t为时间;VF为流体的体积分数;ρ为流体密度;p为压力;Gi为流体各方向的体加速度;fi为流体各方向的黏性加速度。
RANS 方程组为不封闭方程,故须引入湍流模型使方程组闭合。重整化群(Renormalization-Group,RNG)湍流模型能够动态计算最大紊流混合长度,在模拟沉积物冲刷上具有优势且计算时间较短,因此本文采用RNG 湍流模型对控制方程进行封闭。RNG 湍流模型方程包含的湍动能方程和耗散率方程分别采用文献[6]和文献[7]中提出的方程。
1.2 泥沙输运模型
冲刷模型是通过预测泥沙的侵蚀、平流、沉积来描述泥沙的运动。泥沙搬运形式主要有携带、沉积、推移质输沙、悬移质输沙四种。
携带和沉积是同时发生的两个相互对立的过程。当床面切应力超过临界切应力时发生携带,床面泥沙进入悬浮状态。沉积是指泥沙颗粒由于重力从悬浮状态下沉到河床上,或是推移质输沙停止的过程。这两个过程决定了悬移质和推移质的转化率。泥沙起动控制方程和泥沙沉降控制方程分别采用文献[8]和文献[9]提出的方程。
推移质输沙描述泥沙颗粒在河床表面翻滚、跳跃、滑移等现象。推移质输沙控制方程采用文献[10]中提出的方程。
悬移质输沙描述水流携带的泥沙颗粒以高于河床某特定高度进行输运的现象。悬移质浓度通过求解输运方程[5]得到。
2 数值模型与验证
2.1 边界条件和网格划分
在建立冲刷数值模型时,水槽入口设为速度边界,出口设为自由出流边界,底部设为壁面边界,顶部及两侧设为对称边界。
网格划分见图1。x、y、z轴的坐标圆点为初始床面上圆柱(模拟单桩)中心。计算域长度设为20D(D为圆柱直径),宽度设为9D,高度根据试验水深进行调整,模拟冲刷时泥沙的预设高度约为1.2D。
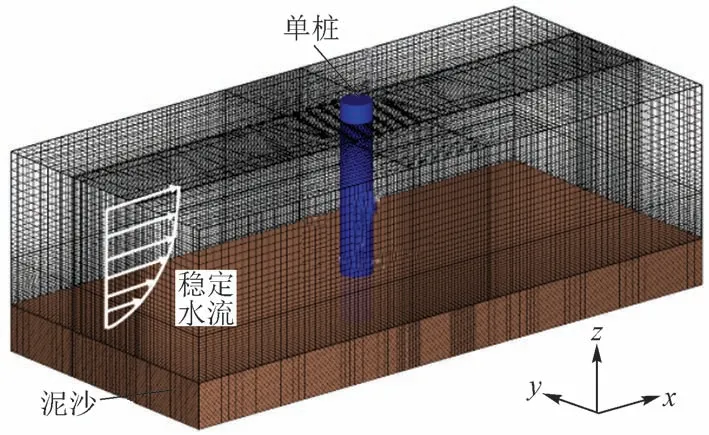
图1 计算域边界情况和网格划分
关于x-y平面内的网格设置,根据文献[11]中网格划分方法,在单桩轴线3D范围内设置较小尺寸(0.075D)的均一网格,从距单桩轴线3D位置至计算域边界设置渐变网格,计算域边界处的网格大小设置为0.3D。关于z方向上的网格设置,将河床表面下方网格大小统一设置为0.05D,从河床表面至上方水面范围内设置渐变网格,水面处网格大小设置为0.3D。
软件中速度边界提供的是沿整个水深的均一流速,与实际流速分布有较大差异。因此,模型建立的第一阶段,先在单柱上游设置一段较长的流速发展区域,在速度入口处输入给定流速,将流速充分发展到沿水深呈对数分布。由于在第一阶段中不考虑冲刷作用,泥沙的动床系数设置为0。在第二阶段,考虑冲刷作用,在速度入口处将第一阶段中得到的对数分布流速剖面引入,模拟流速充分发展时单桩基础的局部冲刷。这种分阶段数值模拟方法在满足计算精度的情况下,可极大减少工作量并提高模拟效率。
2.2 流场验证
在开展数值模拟前,需要对模型进行验证,主要包括流场验证和冲刷深度验证。通过对比现有文献结果与数值计算结果来判断软件能否准确模拟流场变化。选用文献[12]的水槽模型试验数据进行验证,D= 0.536 m,平均流速U= 0.326 m/s,水深h= 0.54 m。单桩周围距河床面垂直距离(z)为0.005、0.05、0.10 m 三个位置流速数值模拟结果与文献[12]试验结果对比见图2。其中从左到右为水流方向,左边为桩前,右边为桩后。
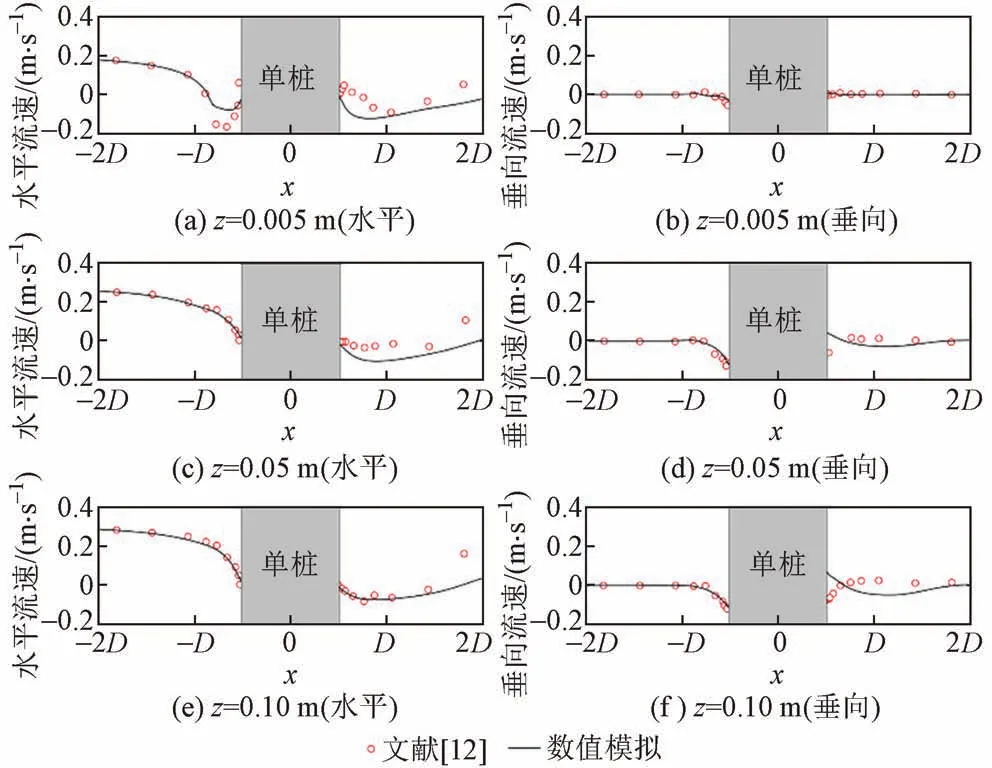
图2 距河床面不同位置水平和垂向流速数值模拟结果与文献[12]水槽模型试验结果对比
由图2可知,无论水平流速还是垂向流速,桩前数值模拟结果与试验结果均吻合较好,而桩后两者略有偏差。这种现象可能与桩后尾涡交替变化相关[13]。单桩基础冲刷很大程度上由桩前流场决定[1-2],虽然桩后流速模拟结果与试验结果略有偏差,但总体上桩周流速与试验结果吻合较好,可以满足研究要求。
2.3 冲刷深度验证
采用文献[14]的水槽模型试验结果对数值模拟冲刷深度进行验证。D= 0.10 m,U= 0.325 m/s,h=0.4 m,泥沙中值粒径d50= 0.324 mm。
单桩周围最大冲刷深度的数值模拟结果与文献[14]水槽模型试验结果对比见图3。可知:随时间延长,数值模拟得出的最大冲刷深度前期发展稍快,后期变缓,与文献[14]试验结果吻合较好。
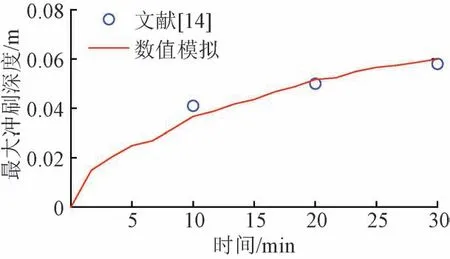
图3 单桩周围最大冲刷深度的数值模拟结果与文献[14]水槽模型试验结果对比
单桩周围冲刷坑形态数值模拟结果见图4。可知:本文数值模型能较好模拟完整的冲刷坑形态,冲刷坑形态大致呈倒锥形。
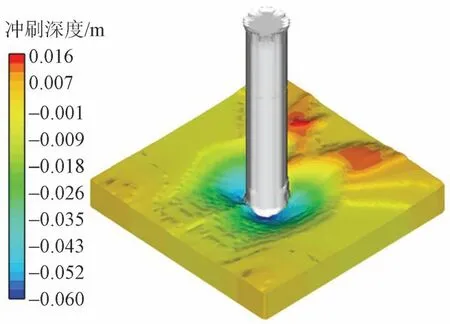
图4 单桩周围冲刷坑形态数值模拟结果
3 影响因素
3.1 平衡冲刷深度和时间尺度
水深与桩径之比大于某值时,水深对冲刷的影响可忽略不计[4,15-16],故本文不考虑水深对冲刷的影响。考虑到数值模拟的计算效率较低,仅开展冲刷时间为30 min 的数值模拟分析。先求冲刷深度时程数据,然后选取合适的冲刷深度公式进行拟合外推,确定平衡冲刷深度。
文献[17]、文献[18]、文献[19]中冲刷深度与时间的关系式分别为
式中:ht为t时刻的冲刷深度;h0为平衡冲刷深度;T为冲刷的时间尺度;a、b、c、d为拟合参数。
分别采用式(3)—式(5)对前30 min 冲刷深度时程数据进行拟合。拟合结果与数值模拟结果对比见图5。
由图5 可知:式(3)得到的冲刷深度偏低,在30 min 后冲刷深度几乎不再发展;式(4)和式(5)的拟合精度均较好,两者结果较接近,但是式(5)采用了四参数指数形式进行拟合,更容易受局部数据的影响,导致拟合的平衡冲刷深度变化较大,因此后续分析中的平衡冲刷深度采用形式更简单且稳定性较好的式(4)计算。
考虑到式(3)—式(5)拟合确定的时间尺度受冲刷历程数据影响较大,引入文献[17]中基于试验结果的时间尺度经验公式来反映平衡冲刷深度的发展。经验公式为
式中:T0为无量纲时间尺度;δ为边界层厚度;θs为希尔兹数;g为重力加速度;γ为泥沙相对密度。
3.2 水流参数
单桩基础平衡冲刷深度和时间尺度随水流流速变化曲线见图6。
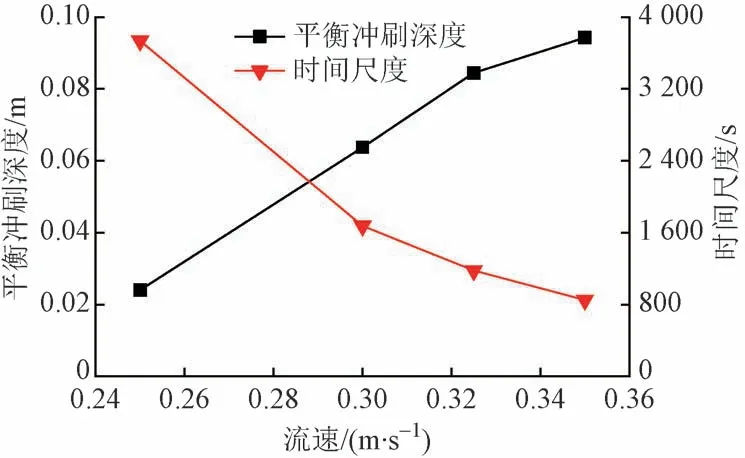
图6 平衡冲刷深度和时间尺度随水流流速变化曲线
由图6 可知:①单桩基础平衡冲刷深度随流速增大而增大,这是因为随着流速增大,希尔兹数与临界希尔兹数的比值增大,从而改变了单桩冲刷的发展速度,使得初期冲刷发展速度加快。②随流速增大,时间尺度显著降低,表明流速增大能减小单桩达到平衡冲刷深度所需时间,反证了冲刷发展速度随流速增大而增大。③流速较小时单桩基础平衡冲刷深度和时间尺度变化十分显著,随流速增大两者变化速率逐渐减小。
3.3 泥沙参数
通过改变泥沙的密度、粒径来研究泥沙参数对圆柱单桩基础局部冲刷特性的影响规律,流速为0.325 m/s。单桩平衡冲刷深度和时间尺度随泥沙参数(密度、粒径)变化曲线见图7。
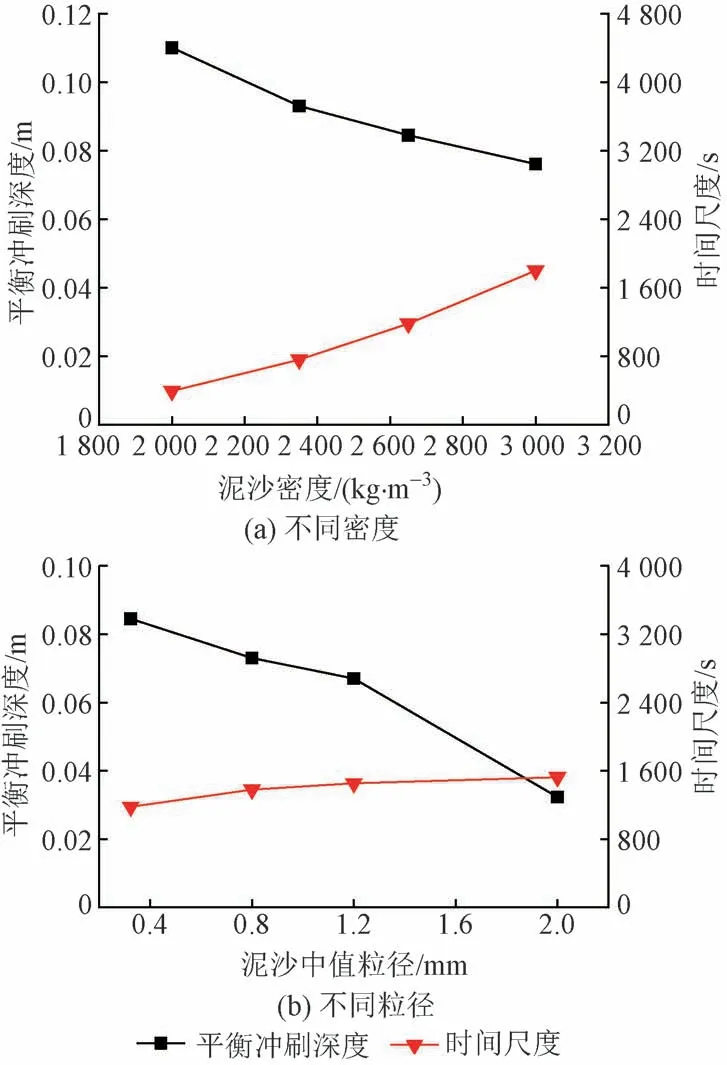
图7 平衡冲刷深度随泥沙参数变化曲线
由图7 可知:①单桩平衡冲刷深度与泥沙密度和泥沙中值粒径均负相关。从无量纲颗粒粒径计算式d*=d50[g(γ-1)/vf2]1/3(vf为流体的运动黏度,取10-6m2/s)可以看出,泥沙相对密度(γ)和d50的增大均会导致d*增大,从而使得希尔兹数与临界希尔兹数的比值降低,水流对河床泥沙的搬运能力减弱,平衡冲刷深度降低。②随密度增加,时间尺度增加较明显;随粒径增大,时间尺度虽有增加趋势,但变化较小。
3.4 单桩直径
在水流和泥沙参数恒定的情况下,改变单桩直径研究结构尺寸对冲刷特性的影响。平衡冲刷深度和时间尺度随单桩直径变化曲线见图8。可知:①不同单桩直径下平衡冲刷深度差异明显。原因是不同单桩直径导致桩前下潜水流和桩周绕流强度不同,从而引起桩周泥沙的希尔兹数发生改变。单桩直径越大,希尔兹数越大,平衡冲刷深度越大。②随单桩直径增大,平衡冲刷深度增幅不大。这是由于D/d50对平衡冲刷深度的影响程度随D/d50的增大而减小[16]。本次模拟时D/d50较大,因此D/d50对平衡冲刷深度的影响不明显。③随单桩直径增大,时间尺度线性增加,变化幅度较小。
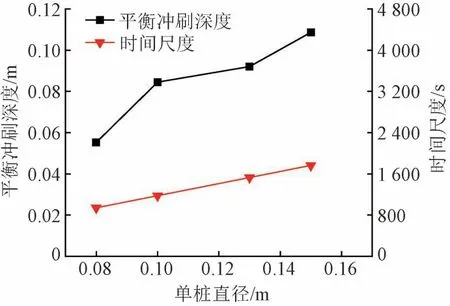
图8 平衡冲刷深度和时间尺度随单桩直径变化曲线
4 结论
本文基于CFD 软件对圆柱单桩基础局部冲刷特性开展了较为系统的数值模拟研究,揭示不同参数对单桩局部冲刷的影响规律。主要结论如下:
1)圆柱单桩基础的平衡冲刷深度随水流流速、单桩直径增大而增大,随泥沙密度和中值粒径增大而减小。主要原因是这些参数的改变会影响桩周希尔兹数与临界希尔兹数之比,从而引起平衡冲刷深度的变化。
2)时间尺度随水流流速增大而减小,随泥沙密度和中值粒径、单桩直径增大而增大。其中水流流速对时间尺度影响较大,泥沙中值粒径对时间尺度影响较小。
