平纹机织复合材料纯电动汽车电池箱多尺度可靠性优化设计

吴自强，陈振中，夏 雨

(1.东华大学 机械工程学院, 上海 201620;2.浙江大华技术股份有限公司,浙江 杭州 310053)

在传统能源危机、环境污染、节能减排理念等多重压力下,纯电动汽车应运而生并取得了蓬勃的发展,与此同时,其续航能力差、安全性能保障低等也成为整个新能源汽车行业亟需解决的问题。研究[1]发现,纯电动汽车的续航和安全性能与自身质量有着密不可分的关系。因此,轻量化逐渐成为新能源汽车行业突破的重点。使用高强轻质材料代替传统金属材料成为轻量化的主流趋势,其中碳纤维复合材料凭借优异的性能和巨大的设计空间,成为轻量化设计领域中应用最广泛的材料[2]。

纯电动汽车的电池系统的质量约占车辆质量的17%～29%,其中箱体是电池系统中除电池芯以外最重的结构。陈静等[3]采用结构优化和多目标优化设计的方法,将复合材料的铺层角度和铺层厚度作为优化变量,对电池箱进行优化设计分析,结果表明,优化后电池箱的轻量化效果显著;胡贺宾[4]在有限元方法的基础上对电池箱进行形貌设计和参数优化设计,优化结果满足电池箱的动静态性能要求;李畇[5]利用Optistruct求解器对电池箱的上盖板进行形貌优化和复合材料的铺层次序优化,优化后的结构能够在满足刚度和碰撞性要求的前提下,实现轻量化。

综上可知,目前复合材料电池箱的优化设计大部分基于复合材料的宏观尺度,即结构优化、拓扑优化和铺层方式优化,而鲜少有关于复合材料细观尺度影响宏观结构性能的研究,因此难以从根本上解决电池箱的轻量化问题。同时,复合材料电池箱的优化设计,必须考虑复杂工作环境和材料内部结构等不确定因素对整体车辆安全性能的影响。但现有研究缺乏对不确定性因素的确定性优化,导致预设安全系数过大,造成材料性能浪费,还有可能导致优化目标函数产生较大波动,使得最终的优化设计结果不可靠。

针对复合材料结构优化设计冗杂和优化结果可靠性低的问题,从碳纤维机织复合材料内部结构的角度出发,采用多尺度联合仿真预测的方法,建立基于均匀化理论的平纹机织复合材料弹性性能预测模型。考虑优化设计过程中复合材料结构存在的不确定性因素,结合Kriging代理模型、SORA(stochastic optimal routing algorithm)法和蒙特卡洛仿真法,提出平纹机织复合材料结构多尺度的可靠性优化流程,以期为平纹机织复合材料在汽车零部件上的优化提供借鉴方法。

1 平纹机织复合材料的弹性预测方法

1.1 复合材料多尺度模型介绍

平纹机织复合材料具有典型的多尺度结构。以纯电动车的电池箱为例,其结构模型如图1所示,其中:纤维与基体树脂组成微观尺度;经纬纱线与基体树脂组成介观尺度;以电池箱结构为宏观尺度,选取单胞体积分数x1为微观设计变量,两相邻纱线之间的间距x2和经纬纱线厚度x3为介观设计变量,每层的铺层角度x4～x9为宏观铺层设计变量。各尺度之间通过均匀化方法传递材料参数,碳纤维复合材料的弹性性能由碳纤维和树脂基体共同决定。

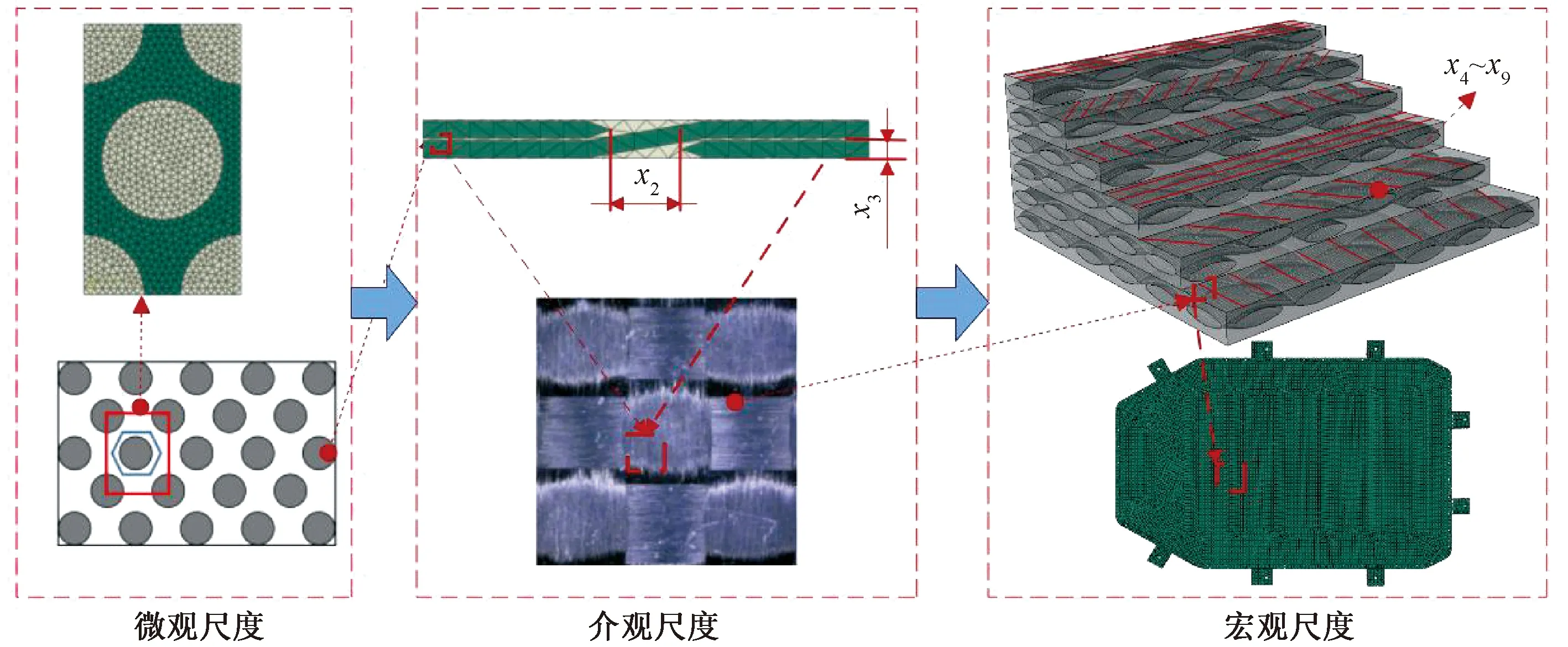
图1 平纹机织复合材料电池箱的多尺度示意图Fig.1 Multi-scale diagram of the plain woven composite

1.2 复合材料的弹性性能预测

1.2.1 利用微观模型预测复合材料的弹性性能

利用细观力学的方法对机织复合材料介观尺度的弹性性能进行预测。为便于计算,将树脂视为各向同性材料,单向纤维视为横向各向同性材料[6]。建立微观尺度坐标系,沿纤维轴向为x轴方向,垂直于纤维轴向的方向分别为y、z轴方向,后续研究用1、2、3代替x、y、z轴方向。根据混合体积定律可得纤维束的弹性性能参数,如式(1)所示。

(1)

式中:Ef11、Ef22分别为纤维轴向和横向的弹性模量;Gf12、Gf13分别为纤维轴向和横向剪的切模量;Vf为纤维的体积分数;μf12为纤维的主泊松比;E11、E22分别为纤维束轴向和横向的弹性模量;G12、G23分别为纤维束轴向和横向的剪切模量;μ12、μ23分别为纤维束轴向和横向的泊松比;Em、Gm分别为基体的弹性模量和剪切模量;μm为基体的泊松比。后续研究机织复合材料的弹性性能时使用的材料为T700/5015环氧树脂单向复合材料,其具体属性参数[7]如表1所示。

表1 碳纤维复合材料力学参数Table 1 Mechanical properties of carbon fiber composite

根据文献[8],建立T700/5015环氧树脂复合材料的等效近似模型。假设介观胞元的总体尺寸为3.60 mm×3.60 mm×0.25 mm,纱线宽度w为1.45 mm,纱线高度hf为0.12 mm,两相邻纱线之间的间距gw=0.35 mm,具体的几何参数如图2所示。

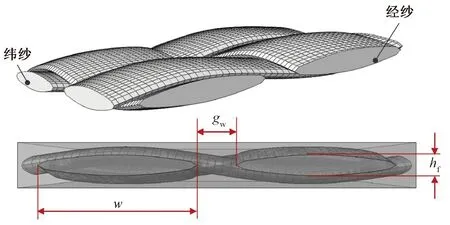
图2 平纹机织复合材料介观尺度几何模型Fig.2 Mesoscale geometric model for the plain woven composite

对于平纹机织复合材料的弹性性能预测:当2种同类型材料的纤维束体积分数相同时,机织胞元的等效弹性参数基本保持一致,因此,根据文献[9]中的数据确定复合材料的总纤维体积分数。近似模型中纤维丝束的体积分数是已知的,计算得出单胞中纤维的体积分数为50.30%,再根据式(1),预测得到该体积分数下纤维丝束的弹性性能,具体参数如表2所示。

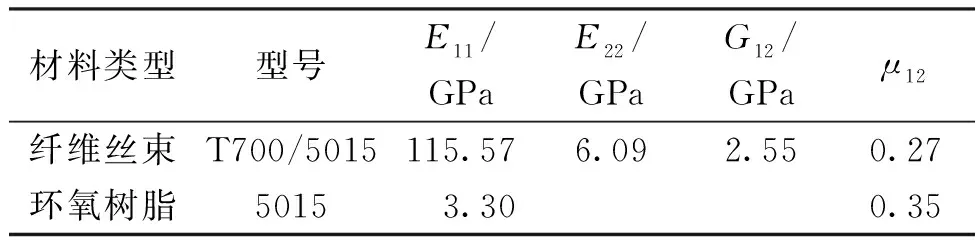
表2 纤维丝束和树脂基体的力学性能参数Table 2 Mechanical properties of fibers and resin matrix

由于平纹机织复合材料弹性力学性能主要由经纬纱线提供,因此经纬纱线要同时参与本身Vf和机织胞元Vf的计算,属于跨尺度计算,无法通过式(1)直接计算得出。基于此,采用基于有限元法的均匀化理论计算弹性参数。

1.2.2 利用有限元模型预测复合材料的弹性性能

利用细观力学的方法对纤维束的弹性性能进行预测。将机织复合材料视为各向异性材料,则其等效本构关系为

(2)

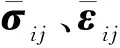
(3)

式中:εij可通过施加周期性边界条件给定。单层层合板尺度可视为由多个胞元均匀周期性排列而成。对于机织胞元,为了避免均匀边界条件难以满足界面处应力连续和位移连续的条件,导致仿真数值分析的准确性降低的问题,必须添加周期性边界条件,其相对两个面的位移差表达式[10]如(4)所示。

(4)

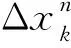
(5)

在ABAQUS软件中调用EQUATION语句,对机织胞元添加纵向、横向的拉伸与压缩,面内、面外的剪切等6种位移边界条件,获取6种等效应力云图,如图3所示。

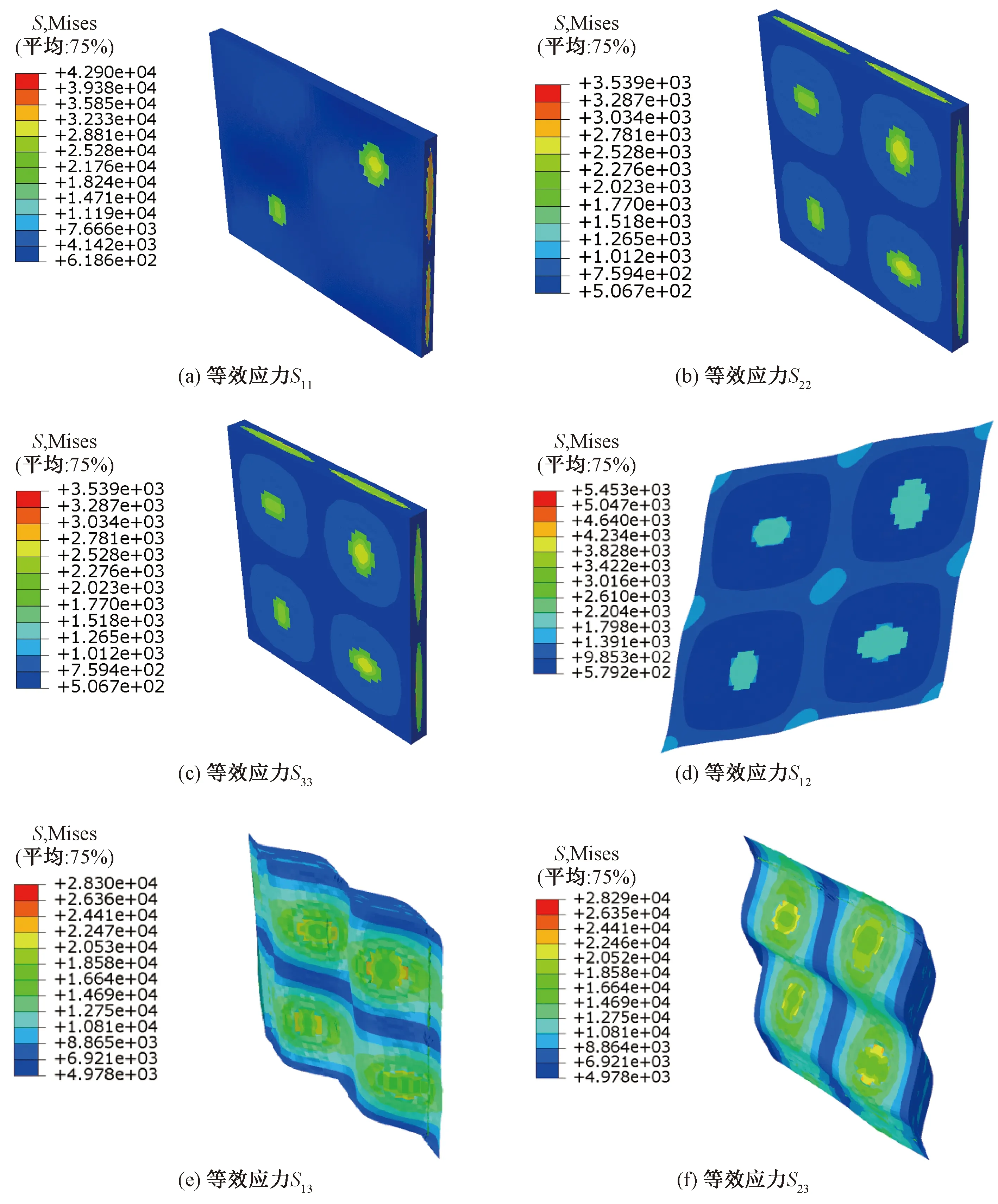
图3 有限元仿真中的胞元应力云图Fig.3 Cellular stress cloud in finite element simulation

根据式(4),将计算得到的弹性参数与试验值[9]进行对比,结果如表3所示。

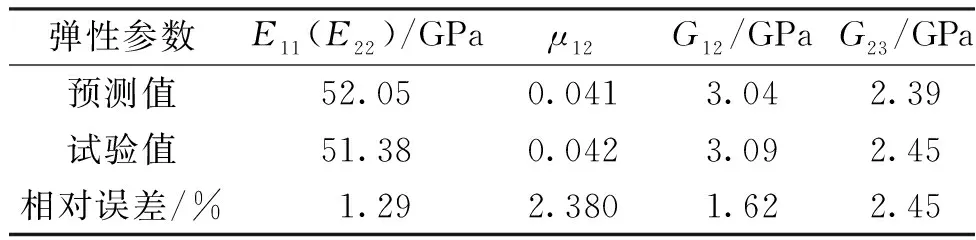
表3 仿真计算值与试验值对比Table 3 Comparison of simulated and experimental results

由表3可知,基于有限元法的均匀化理论求得的参数与试验值的偏差不大,其中,轴向剪切模量G12的相对误差(2.45%)最大。考虑计算和仿真本身所产生的误差,可以认为所提出的预测方法能够准确地预测平纹机织复合材料的弹性性能。

2 钢制电池箱性能分析

2.1 电池箱有限元建模

所研究的电池箱为市面上某款新能源乘用车使用车型,其具体的外观尺寸为1 520 mm×1 002 mm×130 mm,上箱体的厚度为3 mm,下箱体与吊耳厚度为5 mm。整体由钣金工艺冲压而成,材料为Q235碳素钢,总质量为298.6 kg,周边8个吊耳实现电池箱的固定与安装。

电池箱作为纯电动汽车的核心部件,对电动系统的安全性以及整体车辆的稳定性有着重要的影响,因此需要对电池箱做主要仿真分析。电池箱采用壳单元进行网格划分,平均网格尺寸取10 mm,连接处网格尺寸取5 mm,上下箱体之间采用Rbe2连接。所建立的电池箱有限元模型如图4所示。

图4 电池箱的有限元模型Fig.4 Finite element model of the battery box

2.2 仿真工况确定

结合纯电动汽车电池箱仿真的国家标准、汽车企业要求以及电池箱优化的研究现状,建立静强度分析、模态分析和动态挤压分析。

2.2.1 静强度分析

纯电动汽车在正常行驶过程中,电池箱所受到的载荷实时发生变化,箱体内部的电池模组也会因载荷而产生较大的晃动。为了检验电池箱的基础性能在载荷下是否满足要求,拟定垂直颠簸、颠簸转弯、颠簸前进共3种典型工况,各工况的载荷施加情况如表4所示。仿真过程中,设定x轴为汽车制动方向,y轴为驾驶员右侧方向,z轴为垂直地面向下的方向。

表4 3种典型工况的加载情况Table 4 Loading for three typical working conditions

3种典型工况下钢制电池箱的仿真结果性能如图5所示。

由图5可知:垂直颠簸、颠簸转弯、颠簸前进工况下钢制电池箱的位移依次为2.588、1.726、1.728 mm,均发生在钢制电池箱底部中心位置,且均能满足设计要求;其最大应力依次为149.90、97.09、104.90 MPa,均发生在电池箱底部边缘位置,最大应力小于材料的屈服强度,安全系数过大,造成材料浪费。

2.2.2 模态分析

模态为电池箱的固有特性。根据纯电动汽车的真实工作情况以及电池箱与汽车的实际连接关系,采用约束模态对电池箱进行动态性能分析。钢制电池箱的前5阶模态频率分别为21.44、32.89、37.74、51.77、53.45 Hz。根据文献[11],激励频率与车速和路面波长的关系如式(6)所示。

(6)

式中:f为激励频率;v为汽车行驶速度;l为路面波长。取v=100 km/h,l=1.0,计算得到的路面激励频率小于28 Hz,因此一阶模态频率要大于28 Hz。然而钢制电池箱的一阶模态频率为21.44 Hz,低于设计要求。应通过提高模态频率来提高电池箱的结构振动性,避免出现共振现象。

2.2.3 动态挤压分析

模拟纯电动汽车发生碰撞时,电池箱发生变形,侵入箱内电池组。根据蓄电池包挤压的相关国标规定,使用半圆柱对电池箱的横向、纵向分别进行挤压,其中半圆柱以速度v匀速向前,电池箱的动态受力情况如图6所示。当电池箱受到的支反力为100 kN时,要求箱体产生的最大位移不能超过挤压方向整体尺寸的30%,以避免电池箱体与电池模组发生接触从而造成电池模组的破坏。

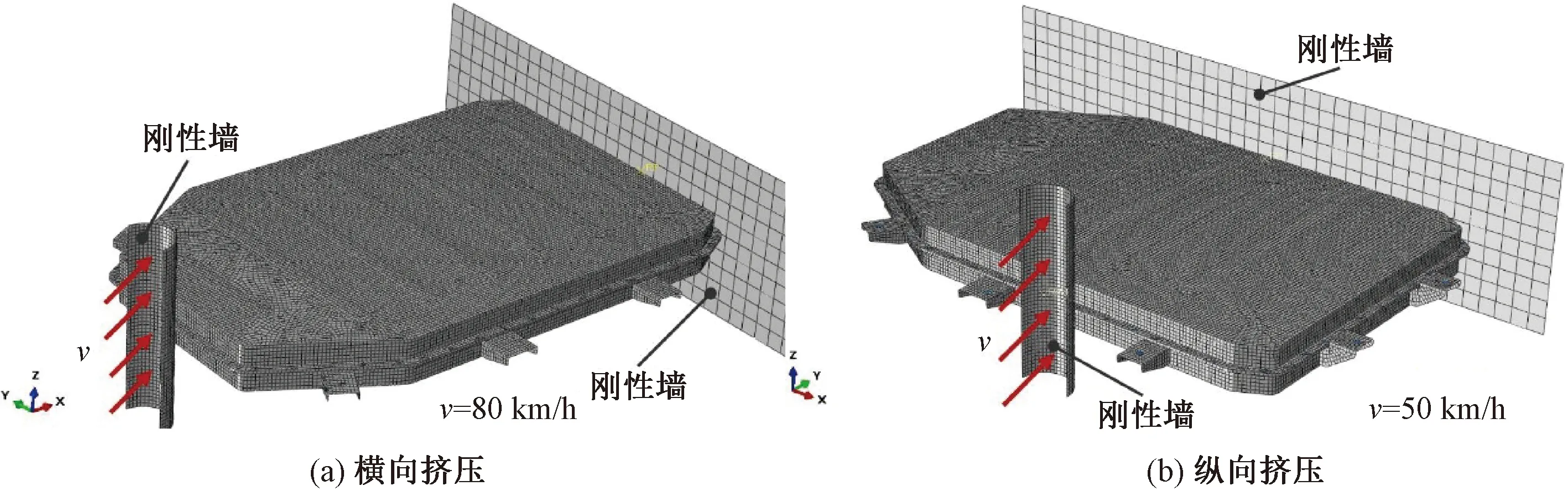
图6 挤压工况下电池箱的受力情况Fig.6 Force on the battery box under extrusion conditions

根据上述标准对钢制电池箱的挤压工况进行分析。挤压工况下钢制电池箱的仿真结果如图7和8所示。由图7和8可知,约在9 ms时支反力为100 kN,此时钢制电池箱横向与纵向的挤压位移分别为42.89和27.67 mm,均低于挤压方向整体尺寸的30%,符合安全性能的要求。

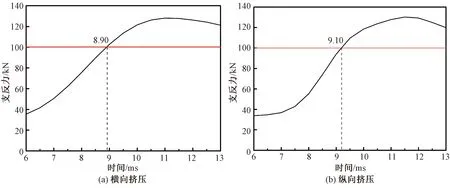
图7 半圆柱受钢制电池箱反作用力曲线Fig.7 Semi-cylinder reaction force curve by the steel battery box

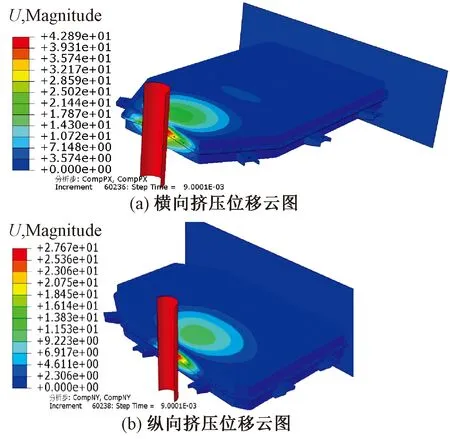
图8 钢制电池箱的挤压工况变形图Fig.8 Extrusion deformation diagram of the steel battery box

3 机织复合材料电池箱多尺度可靠性优化设计

由于纯电动汽车的电池箱长期处在颠簸、磨损等恶劣工况中,受不确定因素影响的可能性较大,因此对电池箱各种性能可靠性的要求更高。根据上文预测得到的复合材料电池箱模型,要求平纹机织复合材料电池箱在不确定因素扰动的情况下,基于可靠性优化方法获得的最优解始终满足工况约束条件,并且最优解不会因为目标函数的波动而失效。不确定性因素对复合材料电池箱性能最优解的影响的示意图如图9所示。

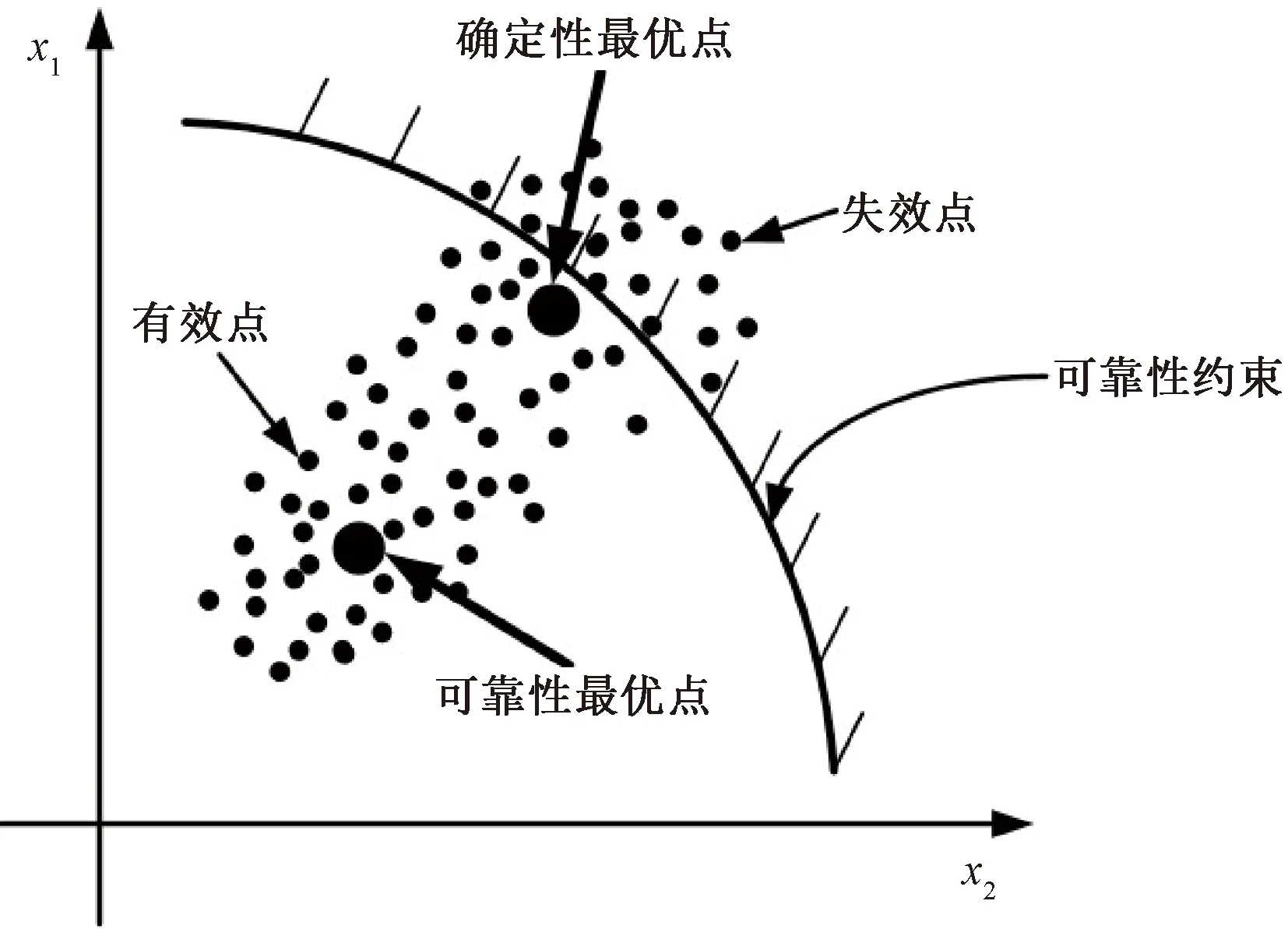
图9 不确定因素对目标函数的影响示意图Fig.9 Schematic of the effect of uncertainty on the objective function

基于可靠性优化设计的数学模型[12]如式(7)所示。

find:t,θx

min:f(t,θx,θp)

s.t.:Prob[gj(X,t,p)≥0]≥Rj,j=1,2,…,N

tmin≤t≤tmax,θx,min≤θx≤θx,max

(7)

式中:t为确定性设计变量;X为随机设计变量;f(t,θx,θp)为目标优化函数;gj(X,t,p)≥0为第j个概率约束函数;Prob[gj(X,t,p)≥0]≥Rj为第j个约束条件的概率;p为随机参数;θx、θp分别为随机参数和随机变量的均值。

3.1 优化设计模型

在平纹机织复合材料电池箱的优化设计问题中,以轻量化为目标,电池箱的质量M为目标函数,将典型工况位移U1、横向挤压工况位移U2、纵向挤压工况位移U3和第一阶模态频率Mode作为约束函数,将钢制电池箱在不同工况下的位移和第一阶模态频率作为优化的基准,要求复合材料电池箱在不同工况下的位移不大于钢制电池箱的位移,第一阶模态频率不小于钢制电池箱的频率。优化过程中涉及的变量如图1所示,其中,x1取值为25%～78%,x2取值为0.05～1.15 mm,x3取值为0.29～0.36 mm,x4～x9为离散变量,角度取值为-45°、0°、45°、90°任意一数值。这些参数在生产过程中均可能存在误差,因此,要将优化设计变量转化为含有不确定性因素的随机变量,此时的确定性约束函数就变为概率性约束函数,从而形成一个可靠性优化设计问题。平纹机织复合材料电池箱的可靠性优化数学模型如下:

(8)

式中:M(x)为电池箱的质量函数;u1、u2、u3为钢制电池箱静态工况、横向挤压工况、纵向挤压工况下的位移;m为钢制电池箱第一模态频率;t1、t2、t3为可靠性优化设计过程中含有不确定性因素的随机变量,彼此相互独立且服从正态分布;βj为可靠度指标。

3.2 优化设计流程

基于有限元仿真实现可靠性优化设计,通常需要花费巨额的计算成本,而通过代理模型进行有限元仿真,仅提供少量的样本及其响应状态,便可搭建输入与输出之间的数学模型。在可靠性优化设计过程中,优化算法直接影响最优解的存在性、求解的迭代效率以及获取的最优解的精确可靠性。平纹机织复合材料电池箱的可靠性优化设计过程如图10所示。具体的优化步骤如下:

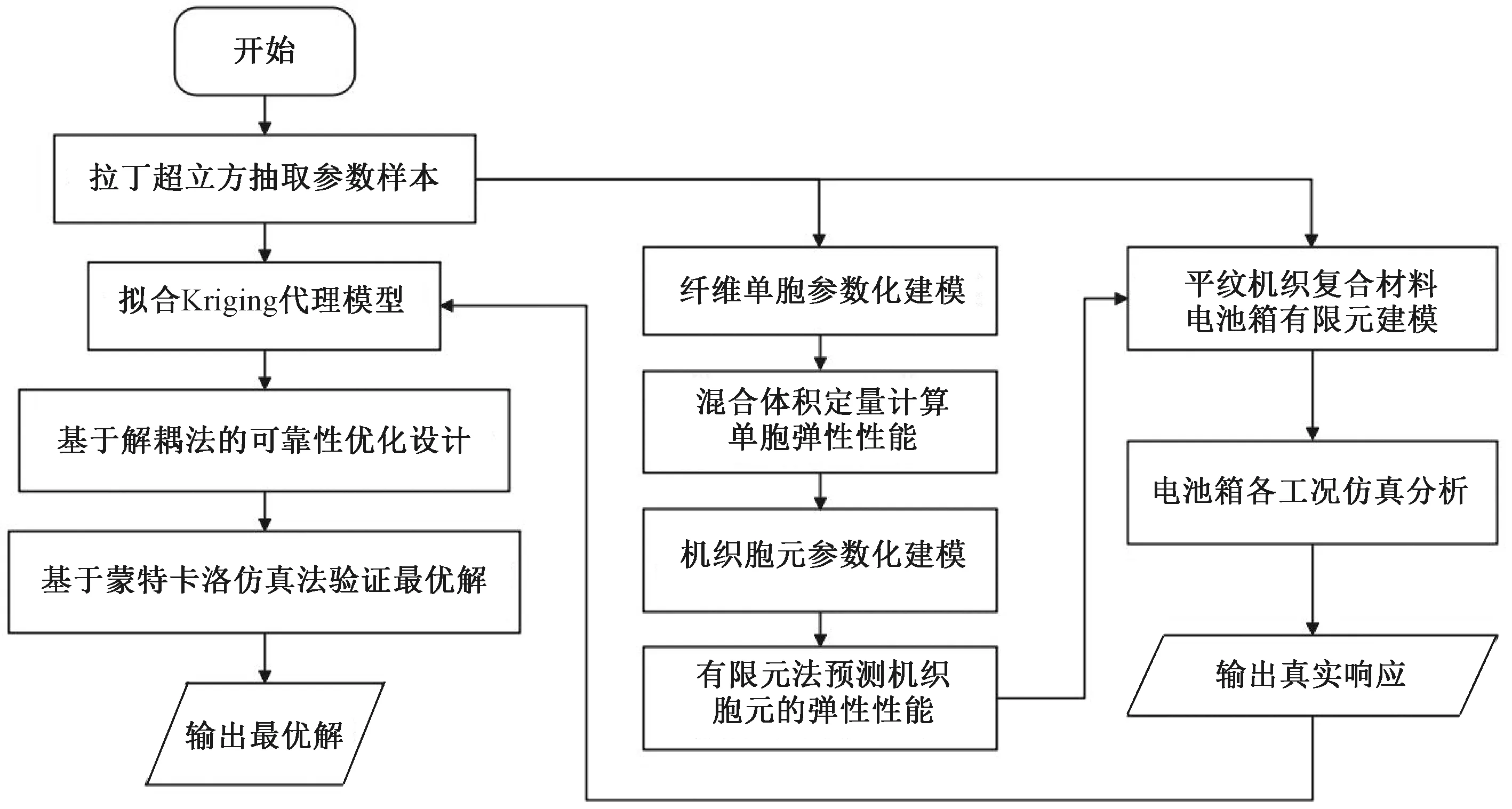
图10 电池箱多尺度可靠性优化设计流程Fig.10 Flowchart of optimizing design of the battery box for multi-scale reliability

——利用拉丁超立方法对所有的设计变量进行抽样,共选取60组设计变量样本。

——根据样本中的材料设计变量,对机织材料进行参数化建模。首先由式(1)计算纤维单胞的等效弹性参数,再通过均匀化理论得到胞元等效弹性参数,最后针对样本中的宏观结构设计变量,联合同一样本下的材料弹性性能,建立不同电池箱模型。

——对所有电池箱模型进行仿真模拟,获取工况下的真实响应。将设计变量与其对应响应值作为输入与输出来拟合Kriging代理模型。采用随机过程方法,利用未知样本点周边领域内已知样本点的信息预测该点的响应[13]。

——将Kriging代理模型嵌入序列优化与SORA法[14]中,每次调用近似模型中不同函数对应的响应值,并判断是否满足约束条件,将符合约束条件的解输出作为最优解。

——基于蒙特卡洛仿真方法[15]对优化设计结果进行可靠度验证,以检验电池箱优化方案的准确性以及可靠性。

3.3 优化设计方法

解耦法具有目前可靠性设计中最为合理的优化结构,其中最常用的方法是SORA算法,其流程如图11所示。SORA算法将基于可靠性的设计优化问题[16-17]分解为可靠性分析和确定性优化两部分序列进行迭代。先用混合均值(hybrid mean value, HMV)法进行可靠性分析,通过可靠性分析后获得当前设计的逆最大可能失效点(inverse most probable poin, IMMP),并将其变换为偏移向量,利用偏移向量将可靠性优化设计模型转化为确定性优化设计模型,以此循环迭代直至找到符合可靠性设计要求的最大可能失效点为止。

4 机织复合材料电池箱优化性能分析

在平纹机织复合材料结构多尺度可靠性优化设计过程中,综合考虑所有约束条件后得到的最优解:微观体积分数为57.88%,纤维丝束间距为0.24 mm,纱线厚度为0.32 mm,铺层角度为45°,0°,90°,0°,-45°,0°,此时机织复合材料电池箱质量为225.2 kg,相比钢制电池箱体(298.6 kg)的质量降低了24.58%。按照钢制电池箱工况分析方法,在施加相同载荷的情况下,检验最优解下机织复合材料电池箱的力学性能。

4.1 静强度分析

机织复合材料电池箱的应力、位移云图如图12所示。垂直颠簸、颠簸转弯、颠簸前进工况对应位移分别为1.112、0.791、0.790 mm,相对于钢制电池箱的工况位移(2.588、1.726、1.728 mm)分别降低57.03%、54.17%和54.28%;对应的最大应力分别为73.46、47.64、51.58 MPa,均小于Q235的屈服强度(235 MPa),并且远低于碳纤维复合材料的屈服强度。蒙特卡洛仿真验证结果表明,最优解能够满足可靠性要求。

4.2 模态分析

获取平纹机织复合材料电池箱前5阶模态频率,分别为29.58、45.51、70.64、83.63、110.36Hz。其中,优化后平纹机织复合材料电池箱的第一阶模态频率能够满足路面激励频率高于28 Hz的设计要求,同时,相比钢制电池箱第一阶模态频率(21.44 Hz)提高了37.97%,二、三阶以及更高阶次的模态频率均有所提高。

4.3 动态挤压分析

挤压工况下平纹机织复合材料电池箱的位移如图13和14所示。当挤压力为100 kN时,优化后的平纹机织复合材料电池箱横向挤压位移为20.51 mm,纵向挤压位移为15.99 mm,相比钢制电池箱(横向挤压位移42.89 mm、纵向挤压位移27.67 mm)分别降低了52.18%和42.21%,蒙特卡洛仿真验证表明,优化结果能够满足可靠性要求。

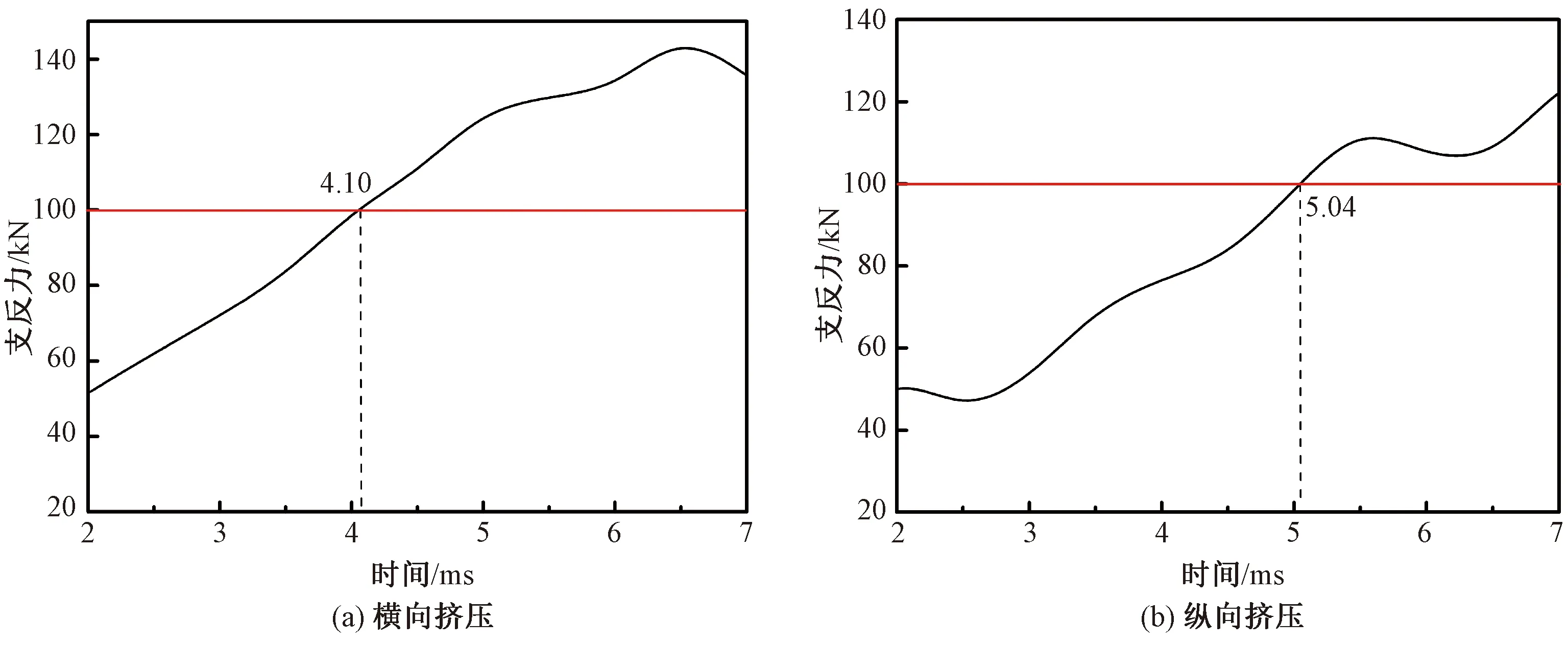
图13 半圆柱受平纹机织复合材料电池箱反作用力挤压的曲线Fig.13 Reaction force curve of semi-cylinder subjected to the plain woven composite battery box

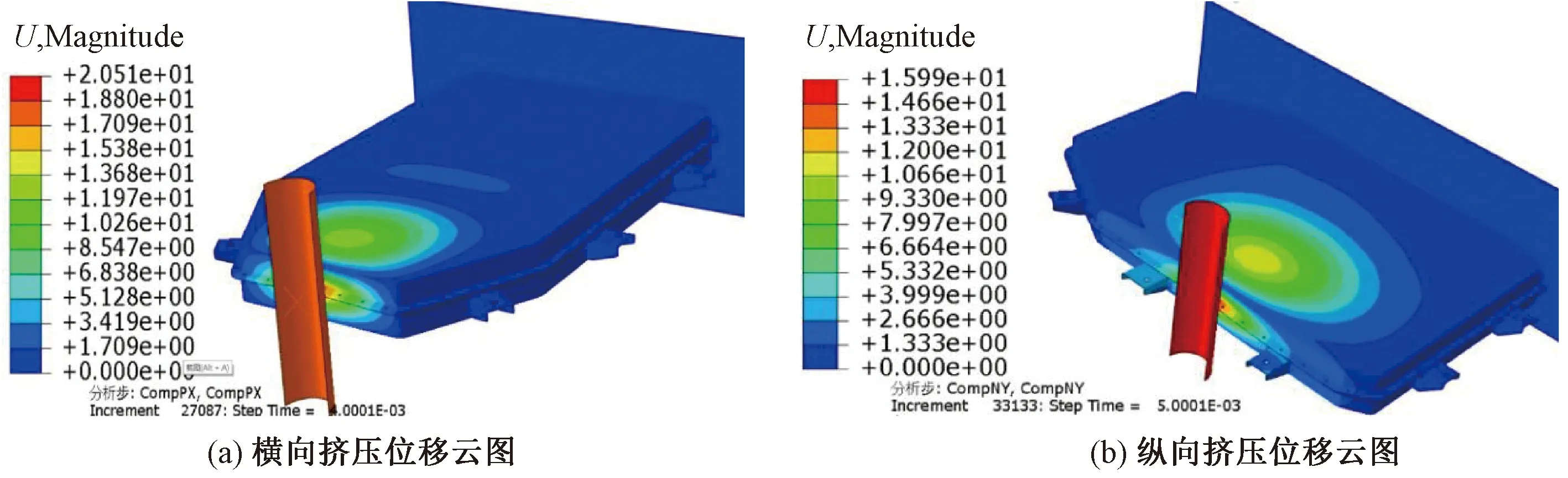
图14 最优解下平纹机织复合材料电池箱的挤压工况变形图Fig.14 Extrusion deformation diagram for the plain woven composite battery box under optimal solution

5 结 论

本文基于有限元法的均匀化理论建立了平纹机织复合材料弹性性能的预测模型,通过编程传递不同尺度之间的材料参数,实现不同设计变量下胞元的有效弹性性能预测。同时,考虑多尺度设计变量存在的不确定性,将确定性变量转换为含有不确定性因素的随机变量,建立基于可靠性的多尺度优化流程,实现对平纹机织复合材料电池箱的优化设计。结果表明:相比钢制电池箱,平纹机织复合材料电池箱的质量减少了24.58%,静强度3种工况下位移分别降低了57.03%、54.17%和54.28%,第一阶模态频率提高了37.97%,横向挤压位移降低了52.18%,纵向挤压位移降低了42.21%。优化结果验证了基于多尺度的复合材料结构可靠性优化设计方法的可行性,为平纹机织复合材料在汽车零部件上的推广应用提供了可借鉴的方法。