基于仿生曲面复眼相机的目标定位技术

朱帅民，郭文阁，刘韬，张远杰，许黄蓉，武登山，周晓军，鱼卫星

（1 西安石油大学 理学院， 西安 710065）

（2 中国科学院西安光学精密机械研究所 中国科学院光谱成像技术重点实验室，西安 710072）

（3 中国科学院大学 光电学院，北京 100049）

0 引言

传统的单孔径成像系统通常只能得到目标的几何图像信息，而复眼视觉系统由于具有大视场、大景深、可获得目标深度信息和对快速运动目标敏感等优点，在深空探测、安防监控、人工智能导航等领域有广泛的应用前景［1-2］。使用视觉系统对目标定位是其对目标进行三维探测的必要步骤，目前常见的方法是利用双目视觉系统根据视差原理来对目标进行定位。然而，双目视觉系统因为只存在一组视差关系，约束条件较少，所以定位精度不是很高。此外双目视觉系统的测量距离与基线大小直接相关，因此远距离测量情况下就要求基线距很大，而大基线距会造成系统体积过大。复眼视觉系统在基线固定的条件下，可以通过增加约束条件从而减小测量误差，因而在目标定位方面具有独特的优势并引起了研究者的关注。瑞士洛桑联邦理工大学的AFSHARI H 等设计研制出了由约100 个子相机组成的复眼相机阵列，每个子相机具有单独视场和焦点，能够实现大视场成像［3］。MALYARCHUK V 等由火蚁复眼得到启发，研制成功了具有180 个子眼的半球型复眼系统，视场范围达到了160°，但该成像系统分辨率不高，成像效果不好［4］。2014 年，四川大学刘艳等通过构建多组双目测量系统，求解空间中目标点的三维坐标并求取平均值，以此来进行目标定位和三维重构［5-6］。该定位方法的精度达到2.53×10-4rad，但由于相机阵列平面分布，所以该定位系统视场较小。2016 年，郭书基等设计制作了19 眼的曲面复眼相机［7］，根据相机针孔成像原理和像素坐标系与空间坐标系的线性关系建立复眼定位模型。2017 年，中国科学技术大学何建争等基于复眼系统特征［8-9］，提出一种基于双球面标定的目标定位方法。距离复眼相机0.83 m 处，定位误差最大为0.5%，但其复眼系统结构复杂，系统装配技术和平台调节都会对定位精度产生影响。2018 年，沈阳理工大学李伦等利用模压成型工艺设计并制作了具有61 个子眼的复眼相机，根据坐标系间的变换关系建立了目标定位数学模型，并进行了目标定位实验，随着参与定位子眼数目的增多，目标定位精度有效提高，当子眼数目达到20 时，定位误差降至10%以下［10］。2020 年，南昌大学高文静等提出一种对目标方位角的快速检测算法，以及基于视差原理的复眼系统定位模型，通过实验实现了对运动目标的方位以及距离测量，在短距离测量范围内，测量误差小于10 mm［11］。2021 年，中国科学院大学袁泽强等设计并制造了包含有17 个子眼的曲面复眼相机。利用该相机设计了基于非平行双目三角测量的目标定位方法［12］，该复眼相机在3.15 m 距离处定位误差最大为2.31%。2022 年，西安光机所刘晋亨等提出了一种基于人工仿生曲面复眼相机的三维测量方法［13］，将捕捉到目标的子眼构造为多组双目系统来对目标进行测量，将多组测量结果的平均值作为最终测量结果。以此方法对目标点进行距离测量及三维成像，在3.2 m 范围内，该方法的测距误差最大为5%。这种测量方法相较于传统的双目测量方法提高了测量精度，增强了鲁棒性。但这种测量方法适用的工作距离较短，误差会随测量距离大幅上升。

本文在实验室研制的仿生曲面复眼相机［14］的基础上研究该相机在三维测量方面的优势，提出了一种适用于复眼相机的目标定位算法。该方法根据目标在子眼像素坐标系中的坐标与在世界坐标系中的坐标的对应关系及标定的复眼相机各子眼相机内外参数建立方程组，使用最小二乘法解方程组来获得目标的空间位置，通过增加约束有效提高了复眼相机的测量精度。根据目标定位算法进行了测距实验，实验结果表明，在4 m 的工作范围内，复眼相机测量误差最大为2%。相较于采用传统双目测量方法［13］，所提测量方法在相同距离3.2 m 处，误差下降了约3.5%。在目标定位基础上利用尺度不变特征转变（Scale Invariant Feature Transform，SIFT）特征检测与匹配算法及随机抽取一致（Random Sample Consensus，RANSAC）优化算法来获取精确的子图像匹配点对，提出了一种三维点云重构算法，设计并进行了物体重构实验，对空间立体目标实现了较好的三维点云重构，验证了仿生曲面复眼相机目标定位和三维重构的可行性和准确性。

1 仿生曲面复眼相机结构

图1（a）和（b）分别为所用曲面复眼相机的原理和实物图。该相机由曲面复眼、光学中继系统和高清晰度图像传感器三个子系统构成，具有实现大视场远距离目标探测、体积小、结构紧凑的特点［15-16］。相机包含了在直径136 mm 的金属半球壳上按照六边形蜂窝状排布的127 个子眼，子眼直径为7.4 mm，单个子眼的视场角为14°，相邻子眼光轴间的夹角为7°。相机系统焦距为5 mm，最大视场约为98°×98°，角分辨率为1.8 mrad，系统尺寸为Ф123 mm×195 mm，总质量为1.35 kg。焦平面探测器采用索尼公司生产的型号为NOIP1SN025KA 的图像传感器，该图像传感器读出帧频为13 帧/s，像元大小为5 120×5 120，像元尺寸为4.5 μm，像面尺寸为23 mm×23 mm。

图1 仿生复眼相机系统Fig.1 Biomimetic compound eye camera system

2 仿生曲面复眼相机定位原理

传统的双目视觉定位方法是基于同一目标点在两台相机成像平面上的位置偏差来测量深度信息，这种测量方法受两台相机之间基线的约束，在远距离测量中误差较大，且两台相机只有一组约束条件。与双目视觉定位相比，基于仿生曲面复眼相机的多目定位技术通过增加参与目标定位子眼的数目，进一步增加了约束条件，从而有效提高了目标定位精度。

2.1 物像直线模型

如图2，设空间目标中特征点P在世界坐标系中的坐标为（XW，YW，ZW），其在仿生复眼相机的某子眼像素坐标系上的投影像素坐标为pi（ui，vi），考虑到仿生复眼相机的结构和子眼大小，可用针孔成像模型得到P与pi的关系，表示为

图2 复眼定位原理Fig.2 Positioning principle of compound eyes

式中，zc为尺度因子，fx、fy为子眼焦距，（u0，v0）为主点坐标，fx、fy、u0、v0为子眼内部参数。R、T为子眼外部参数，R为旋转矩阵，T为平移向量。由式（1）可以得到一条通过pi、P两点的直线，而至少两条直线相交才能确定一点位置，所以最少需要两个视场重叠的子眼才能对特征点定位。特征点与其在两个子眼图像上的像点定义两条直线，这两条直线相交于空间中的一点即为被测特征点。将双目定位推广到多目定位，多条直线相交于一点可以使特征点定位更加准确。

2.2 多目定位数学模型

如图2，空间中点P在子眼1、2、3、4 的图像平面上的像点分别为p1、p2、p3、p4。令世界坐标系与子眼1 的相机坐标系重合，那么子眼1、2、3、4 的像素坐标系与世界坐标系的变换关系可表示为

式中，zi（i=1，2，3，4）为尺度因子，Ki（i=1，2，3，4）为各子眼的内部参数矩阵；Ri（i=2，3，4）、Ti（i=2，3，4）分别为各子眼相对于1 号子眼的外部参数，子眼内外参数可由相机标定获得；像点像素坐标（ui，vi）（i=1，2，3，4）由MATLAB 软件编写程序获得。由式（2）建立超定方程组，利用最小二乘法解方程组即可求得目标在世界坐标系中的三维坐标。

2.3 视场重叠分析

图3（a）给出了实验室研制的仿生复眼相机相邻子眼的两种排布方式，A、B两个相邻子眼光轴夹角为7°，C、D两个相邻子眼光轴夹角为12.13°。图3（b）为相邻子眼视场重叠示意，用来分析相邻子眼视场重叠以获得双目定位和四目定位的临界物距l。由几何关系可得

图3 相邻子眼重叠视场分析Fig.3 Analysis of overlapping fields of view for adjacent sub eyes

由仿生复眼相机结构可知，b=68 mm，为复眼支撑球壳半径；α=7°或12.13°，为相邻子眼光轴夹角；β=14°，为子眼视场；d表示两相邻子眼边缘视场交点与复眼相机子眼排布曲面的中心位置之间的长度。经计算可得，两种相邻子眼发生视场重叠的临界物距分别为67.5 mm 与436.9 mm。即距离l>67.5 mm 时，两个子眼发生视场重叠；当距离l>436.9 mm 时，4 个子眼发生视场重叠。因为单个子眼视场角只有14°，所以最多有4 个子眼视场能同时拍摄到同一个特征点，即最多有4 个子眼能够对空间点进行定位。

3 仿生曲面复眼相机标定

采用张正友标定法利用平面标定板对复眼相机参数进行标定，传统平面标定板必须完整被相邻子眼同时拍摄到，否则无法识别角点空间坐标。本文所用的具有127 个子眼的复眼相机单个子眼的视场较小，很难拍摄到完整的棋盘格，因而引入一种新的标定靶标CALTag（CALibration Tag）标定板［17］，CALTag 标定板在传统平面标定板的基础上添加了编码信息，因为其每个标记都是唯一的，可以从数据表格中查找丢失的标记，所以在标定板部分被遮挡或者拍摄不完整的情况下依然可以进行相机标定。除此之外，在光照条件变化较大和拍摄角度差的情况下也能进行相机标定，因此可以用于复杂环境中的相机标定。除了应用于相机标定，自识别标记也可应用于机器人视觉导航以及增强现实等领域。

利用Hough 圆检测算法检测出各子眼的子图像的圆心，如图4（a）。根据子眼的圆心坐标对子眼进行编号，如图4（b）。

图4 圆心检测和子眼排序Fig.4 Center detection and sub eyes sorting

使用复眼相机改变相机位置和姿态拍摄35 幅标定板图像，保证每个子眼拍摄到的标定板能覆盖整个视场。图5（a）为复眼相机对标定板拍摄一次获得的原始图像。图5（b）为对应的中心子眼子图像。

图5 复眼相机拍摄到的标定板图像Fig.5 Calibration board image captured by compound eye camera

通过单目标定得到的部分子眼内部参数如表1。根据内部参数的标定结果计算重投影误差均在0.3 pixels 以下，cx、cy表示相机光轴在图像坐标系中的偏移量，以像素为单位。

表1 部分子眼内部参数Table 1 Internal parameters of some sub eyes

以1 号子眼相机坐标系为基准坐标系，部分相邻子眼外部参数矩阵如表2。因为旋转矩阵元素的对称性，旋转矩阵R可转换为旋转向量Rom，T为平移向量。

表2 部分相邻子眼的外部参数Table 2 External parameters of some adjacent sub eyes

4 仿生曲面复眼相机测距实验

基于所述的目标定位算法以及相机标定，设计了仿生曲面复眼相机测距实验以衡量其测距精度。实验器材包括激光测距仪、用于形成光斑的纸板和仿生曲面复眼相机。首先将复眼相机固定放置，调整激光测距仪使激光投射至子眼中心，然后固定激光测距仪。激光测距仪到子眼的直线距离作为基准距离L，将纸板放置在测距仪与复眼相机之间，使用激光测距仪测得测距仪与激光光斑的直线距离为M，则可得到光斑与复眼相机之间的距离Z为L-M，如图6（a）。复眼相机拍摄到光斑的图像如图6（b）。实验选用型号为ZBLW-40，工作范围为0.05～40 m，测量精度为±2 mm 的激光测距仪，激光测距仪发射的激光波长为650 nm，激光功率为1 mW。从900 mm 开始，以每次600 mm 的步长将光斑远离复眼相机，每次移动记录光斑与激光测距仪的距离。

图6 光斑定位示意Fig.6 Schematic of light spot location

采用MATLAB 软件编写程序，利用灰度质心法获得光斑质心在各子眼像素坐标系中的坐标。根据所述定位模型，得到光斑质心空间坐标为（x，y，z）。光斑与复眼相机的距离X可表示为

测量相对误差ΔP的表达式为

如图6（b），以n1号子眼为基准，其他3 个相邻子眼分别与n1号子眼组成3 组双目测量系统，3 组三目测量系统以及1 组四目测量系统。根据所述目标定位原理分别利用不同目数的测量系统对光斑距离复眼的距离进行测量。

图7 为3 组双目测量系统、3 组三目测量系统以及四目测量系统的测量结果对比。3 组双目测量系统在4 m 工作范围内的平均测量误差为2.32%；3 组三目测量系统在4 m 范围内的平均测量误差为1.73%；四目测量系统在4 m 工作范围内的平均测量误差为1.44%。实验结果表明，随着参与测量的子眼数目的增加，测量误差逐渐减小。这是因为子眼数目的增多使解算光斑空间坐标的方程数目增多，增加了计算约束从而减小了测量误差。

图7 不同目数的测量系统测量结果对比Fig.7 Comparison of measurement results of measurement systems with different sub eye quantity

实验过程中，激光测距仪在每次发射激光时因人工操作发生轻微抖动，使激光投射在纸板上的光斑在相机成像平面上的质心位置发生偏移，给测量结果带来一定误差。通过实验对这种误差进行定量分析。

将激光测距仪与复眼相机相对放置，以每次0.6 m 的步长移动纸板，每次拍摄15 张光斑图像，求取15 幅图像的光斑质心坐标（xi，yi）（i=1，2，…，15），计算光斑质心坐标x方向和y方向的平均值与标准差，标准差可表示为

激光光斑的尺寸随光斑与复眼相机之间的距离增大而逐渐减小。已知复眼相机单个像素大小约为4.5 μm。以图6（b）中的n1号子眼所拍摄到的光斑为例，对不同距离处的光斑进行圆拟合处理，随着距离增大，光斑尺寸变化如表3。

表3 不同距离光斑尺寸Table 3 Spot size at different distances

表4 为与复眼相机不同距离处，n1号子眼子图像中光斑质心坐标在图像坐标系中x，y坐标轴上的偏差。

表4 不同距离光斑质心坐标偏差Table 4 Coordinate error of centroid of light spot at different distances

按以上方法计算拍摄到光斑的子眼子图像中光斑质心坐标的偏差，将平均值作为光斑质心坐标真值m（xi，yi），测量坐标为m'［（x+Δx）i，（y+Δy）i］，Δx和Δy为光斑质心坐标偏移标准差。利用所述目标定位数学模型求得其在空间坐标系中的三维坐标分别是M（X，Y，Z）、M'（X'，Y'，Z'），误差p表示为

由此可以计算得出在不同距离处激光测距仪抖动对目标定位造成的误差，如表5。

表5 光斑质心偏移引起的定位误差Table 5 Positioning error caused by centroid shift of light spot

表5 为不同距离处因激光测距仪抖动导致的定位误差。随着测量距离的增加，激光测距仪抖动造成的光斑质心偏差增大，进而导致定位误差变大。

5 仿生曲面复眼系统三维重构实验

根据前述的仿生曲面复眼样机进行空间目标的三维重构实验，以覆盖斑点的正方体作为重构目标。三维重构实验中选用的正方体边长为55 mm，正方体每个面上覆盖11×11 个黑色斑点，斑点直径为4 mm，相邻斑点圆心间距约为6 mm。因为相机分辨率有限，为了尽可能多地得到匹配点对，根据目标的大小在距离相机约600 mm 处对正方体进行拍摄。

对原始图像进行分割，选择完整拍摄到目标的两幅子图像。利用MATLAB 编写程序，使用SIFT 特征检测和匹配算法进行子图像的粗匹配，得到1 154 组匹配点对，如图8（a）、（b）。然后使用RANSAC 算法去除错误匹配点，得到665 组精确匹配点对，如图8（c）。

图8 特征点匹配流程Fig.8 Feature point matching process

对子图像特征点进行匹配之后，得到特征点在不同子眼像素坐标系中的像素坐标，根据所述复眼定位算法求得各特征点在空间坐标系中的三维坐标，得到目标重构点云，并根据点云深度信息对重构点云进行渲染，如图9。点云颜色由近到远逐渐变化，真实反映了目标的深度信息。因为相机分辨率及周围环境光照因素影响，部分特征点未能匹配，导致重构点云部分区域缺失。

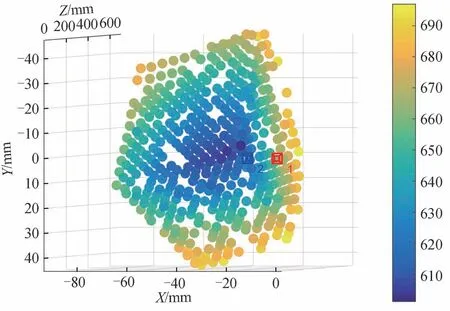
图9 目标重构点云Fig.9 Reconstruction point cloud of the target

为了验证三维重构的精度，以斑点圆心作为特征点，根据特征点在像素坐标系中的像素坐标对应的空间坐标，计算两个特征点之间的距离作为测试值，与待测目标上对应的两个特征点之间距离的真实值进行对比，以此衡量三维重构的精度。其中，每两个相邻斑点的圆心间距为6 mm。选取5 组斑点，对它们的距离进行计算，计算结果如表6。

表6 特征点间距测量结果Table 6 Measurement results of feature point spacing

5 组测量值与真实值比较误差均在2%以下，说明仿生曲面复眼相机可以对空间目标进行较高精度的三维重构。误差主要来源于：环境光照条件不均匀以及复眼相机分辨率不是很高，造成特征点匹配的精度降低，重构出的三维点云存在误差。

6 结论

本文提出一种基于实验室自研的仿生曲面复眼相机的多目定位数学模型，采用CALTag 标定板结合MATLAB 标定工具箱对复眼相机内外参数进行标定。根据定位模型开展了定位实验，实验结果表明，在4 m 的工作范围内，复眼相机测量误差最大为2%，有效提高了相机的定位精度。结合特征点匹配算法与目标定位数学模型建立点云重构算法，实现了空间目标的三维点云重构。研究结果表明仿生曲面复眼相机在目标定位、三维重构以及光学导航等领域具有很大的发展潜力和应用前景。