离散元法中所用土壤参数测量及标定方法研究
2023-10-08林晓君陈松涛耿令新
庞 靖,林晓君,陈松涛,耿令新,周 浩,金 鑫
(1.河南科技大学农业装备工程学院,河南洛阳 471003;2.河南省机械装备先进创造协同中心,河南洛阳 471003;3.潍柴动力股份有限公司,山东潍坊 261000)
我国农业土壤种类多样,在离散元仿真软件里要涉及很多土壤参数,而明确土壤参数是进行正确仿真的前提。部分科研工作者或学者没有合适的测量工具测量土壤参数,因此选择合适的土壤参数测量和标定方法可以有效解决这一问题。离散元是一种可以将介质整体视为若干颗粒单元集合的数值模拟方法[1],在散落物料流动性、固体破碎及机器-土壤相互作用方面具有广泛应用[2-3]。由于土壤特性复杂,有限元土壤模型准确性不高,且只能模拟土壤破坏行为,无法模拟土壤运动过程[4],而离散元可以解决散粒之间及边界间的接触作用,利用黏连颗粒模拟生成土壤团聚体,极大提高了土壤模型的准确性[5]。
目前,土壤的本征参数如固体密度、剪切模量和泊松比等可以通过仪器进行测量,而接触参数难以通过常规测量方法获得,因此很多学者通过离散元对物料参数进行标定的方法获得,主要包括以堆积角和滑动摩擦角为指标的参数标定法。冯俊小等[6]、刘文政等[7]、郝建军等[8]、王黎明等[9]采用离散元法分别对秸秆、马铃薯、油葵籽、猪粪进行了分析和标定。孙景彬等[10]以坡地黏壤土为研究对象,针对Hertz-Mindlin with JKR Cohesion接触模型,以土壤颗粒的仿真堆积角为响应值标定了土壤颗粒间接触参数,通过静摩擦、斜板及碰撞等试验得到了土壤与65Mn钢之间静摩擦因数、滚动摩擦因数和恢复系数的范围;宋少龙等[11]用Hertz-Mindlin(no slip)作为接触模型,通过土壤堆积和滑落试验标定土壤间和土壤与65Mn钢间的系数;张晋[12]用烘干法测土壤含水率,用筛分法测土壤质地,针对Hertz-Mindlin with bonding模型,测土壤堆积角和坚实度来标定土壤之间及土壤与其他部件间的参数。不同的物料以及不同的土壤接触参数都存在一定的差异,标定所用的接触模型不同得到的结果也会有差距,对于坚实度特别小的松软土壤如耕后土壤,上述研究结果已经不适用。
为了提高离散元法针对松软土壤研究的适应性和准确性,该研究选用Hertz-Mindlin with JKR黏结模型作为土壤接触模型,对于该模型所涉及的土壤泊松比、固体密度、剪切模量进行参数测量;采用堆积角和滑动摩擦角试验方法,对土壤间及土壤与触土部件间的恢复系数、动静摩擦系数和土壤表面能进行参数标定及优化,在优化后的参数下建立土槽仿真模型,并进行贯入阻力的室内试验与仿真试验对比,验证所测参数和标定参数的准确性,为松软土壤的仿真参数设置提供参考。
1 土壤本征参数测量
该研究以河南孟津林沟村(34°39′47″N、112°26′04″E)的土壤为试验对象,通过比重计法测量,得到土壤颗粒直径小于0.01 mm的占11%,土壤颗粒直径在0.01~<0.05 mm的为28%,土壤颗粒直径在0.05~<1.00 mm的为49%,≥1.00 mm的为12%,根据土壤质地分类表得到土壤质地为砂壤土。由于土壤泊松比、剪切模量等参数受土壤含水率的影响,因此该研究所测土壤均在含水率为(15±1)%的条件下测量,其他含水率下的测量方法与此相同。
1.1 固体密度的测量土壤密度分为固体密度和体积密度,体积密度含有孔隙和空气,与压实程度有关,而固体密度是土壤本身的密度,与压实和空气无关。仿真软件EDEM所涉及的土壤密度为固体密度,该研究通过体积置换法[17]测量土壤的固体密度,如图1所示。

图1 体积置换法Fig.1 Volume displacement method
取少量土壤并将土壤充分烘干,得到土的质量(Ms)为123.2 g,所用容器的体积(Vr)为400 cm3。先将水注满容器,得到水的质量(Mw)为410 g,由此得到水的密度:
(1)
式中:ρw为水的密度(g/cm3);Mw为注满水的质量(g);Vr为容器体积(cm3)。
将烘干的土壤放入容器中,再将容器注满水,用水置换出烘干土壤中的间隙和空气。称量注满水后土壤颗粒与水的总质量(M″)为484 g,因此得到补充水的质量(总空隙充水质量)和体积:
M′w=M″-Ms
(2)
(3)
式中:M′w为补充水的质量(g);M″为土壤与水的总质量(g);Ms为土壤的质量(g);V′w为补充水的体积(cm3)。
恒容容器的总体积与补充水的体积之差得到土壤的体积和固体密度:
Vs=Vr-V′w
(4)
(5)
式中:Vs为土壤体积(cm3);ρs为土壤固体密度(g/cm3)。
土壤密度一般在2.6~2.8 g/cm3[13-14],将该试验所用土壤通过体积置换法得到土壤的固体密度为2.566 g/cm3,符合基本的土壤密度。
1.2 泊松比泊松比是反映材料横向正应变与轴向正应变的绝对值的比值,通过直接剪切试验(图2)可以测量土壤泊松比。

图2 直剪试验Fig.2 Direct shear test
通过绘制抗剪强度与垂直压力的关系曲线图,得到土壤的内摩擦角(φ)为26°,通过公式(6)和(7)得到土壤泊松比为0.36。
K=1-sinφ
(6)
(7)
式中:K为土壤测压力系数;φ为土壤的内摩擦角(°);v为土壤泊松比。
1.3 弹性模量与剪切模量弹性模量是衡量材料抵抗弹性变形能力大小的标尺。试验时先将土壤做成标准大小的圆柱形土样,土样的直径(D)和高(L)均为50 mm,用万能试验机(DNS02-1KW)以1 mm/s的速度对土样施加载荷,并读取力(F)和变形(ΔL)的数据,直至土壤应力呈下降趋势达到压溃效果,共做5组试验,由公式(8)~(10)计算出土壤弹性模量的平均值为8 MPa,并由公式(11)得到土的剪切模量为2.99 MPa,试验过程如图3所示。

图3 土样压溃试验Fig.3 Crushing test of soil sample
(8)
(9)
(10)
(11)
式中:ΔL为土样受压后的变形量(m);L为土样原来高度(m);D为土样直径(m);A为土样接触面积(m2);F为土样受到的轴向载荷(N);E为弹性模量(Pa);G为剪切模量(Pa)。
2 土壤参数仿真标定
2.1 土壤堆积试验通过测量堆积角,可以用来标定土壤颗粒间的碰撞恢复系数、静摩擦系数、动摩擦系数和土壤表面能。采用漏斗测定土壤颗粒的堆积角,如图4所示,漏斗的出口直径为27 mm,出口距水平面的高度为75 mm,试验中对土壤颗粒进行5组试验,每组试验都从4个方向测量角度并求平均值,最后得到5组试验的平均值作为休止角,通过试验测得含水率为(15±1)%时土壤休止角为36.43°。

图4 堆积试验Fig.4 Stacking test
土壤颗粒直径大小不一,土壤粒径是非常小的,在仿真计算时土壤模型的尺寸一般会比真实的土壤颗粒大,根据工况可以将土壤粒径放大10~50倍,在此设定土壤颗粒粒径在0.5~1.5 mm。
通过文献[15-17]以及EDEM里的GEMM Wizard材料库,设定土壤颗粒间的恢复系数A(0.2~0.6)、静摩擦系数B(0.3~0.7)、动摩擦系数C(0.1~0.4)、土壤表面能D(0.02~0.10 J/m2)。最陡爬坡试验可以较快地确定因素最优值所在区间,由表1可知,随着参数的增大,堆积角呈增大趋势,2号水平最接近试验结果,因此选择1、2、3组试验所选的水平进行中心组合试验(CCD)。试验因素和水平编码如表2所示,根据试验设计,确定编码系数γ为2,中心组合试验结果如表3所示,其中相对误差(δ)的计算方法由下式确定:

表1 最陡爬坡试验方案及结果

表2 中心组合试验因素水平编码

表3 中心组合试验及结果
(12)
式中:a为休止角的试验值;a1为休止角的仿真值;δ为相对误差。
应用软件Design Expert 8.0.6对试验结果进行分析,得到二次回归的模型。该二次回归模型的方差分析如表4所示,该回归模型P<0.000 1,说明休止角相对误差与所得回归方程关系是十分显著,失拟项P=0.452 3>0.05,说明所得回归方程的非正常误差所占比例很小。该试验的相关系数(r)为0.995 7,因此所得回归方程可靠度较高。

表4 中心组合试验回归模型方差分析
通过回归分析得到的误差回归方程为
δ=234.03-182.43A-344.42B-708.35C-1 454.75D+272.25AB-405.75AC+1 488.75AD-22.75BC+1 033.75BD+2 513.75CD+153.63A2+299.13B2+1 084.12C2-696.88D2
应用Design Expert 8.0.6软件以休止角的相对误差为目标对回归方程求解寻优,得到土壤间相关系数(r)的最优值,土壤-土壤恢复系数A为0.28,土壤-土壤静摩擦系数B为0.49,土壤-土壤动摩擦系数C为0.24,土壤表面能D为0.04 J/m2。
2.2 土壤滑落试验通过土壤滑落试验(图5),测量滑动摩擦角可以标定土壤与触土部件的碰撞恢复系数、静摩擦系数和动摩擦系数。采用的钢板长250 mm、宽190 mm,在钢板一侧放置少量的土壤颗粒,斜面沿转轴缓慢旋转,当土壤由一侧滑落到另一侧时,测定土壤的滑动摩擦角。试验中进行5组试验,求平均值得到土壤滑动摩擦角为32.63°。

图5 土壤滑落试验Fig.5 Soil sliding test
在仿真中为了平衡仿真时间仍将土壤颗粒半径设置为0.5~1.5 mm,根据文献[18-21]设定土壤与触土部件的恢复系数E(0.2~0.6)、静摩擦系数F(0.3~0.7)、动摩擦系数G(0.01~0.20)。由表5可知,4号水平最接近试验结果,因此选择3、4、5组试验所选的水平进行中心组合试验(CCD)。试验因素水平编码如表6所示,编码系数γ为1.682。
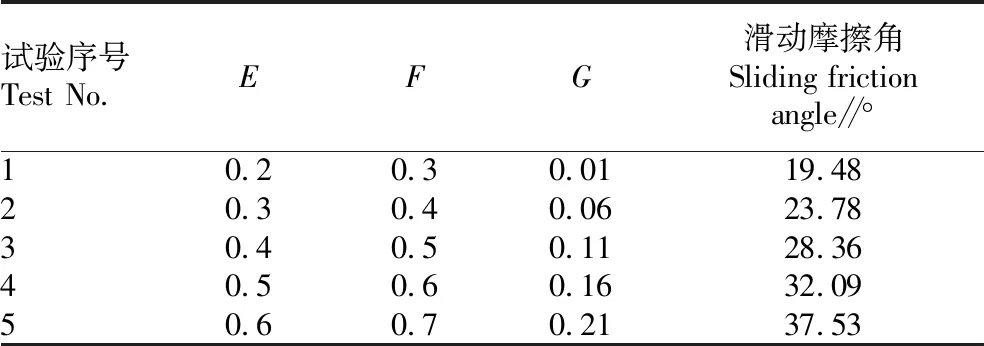
表5 最陡爬坡试验方案及结果
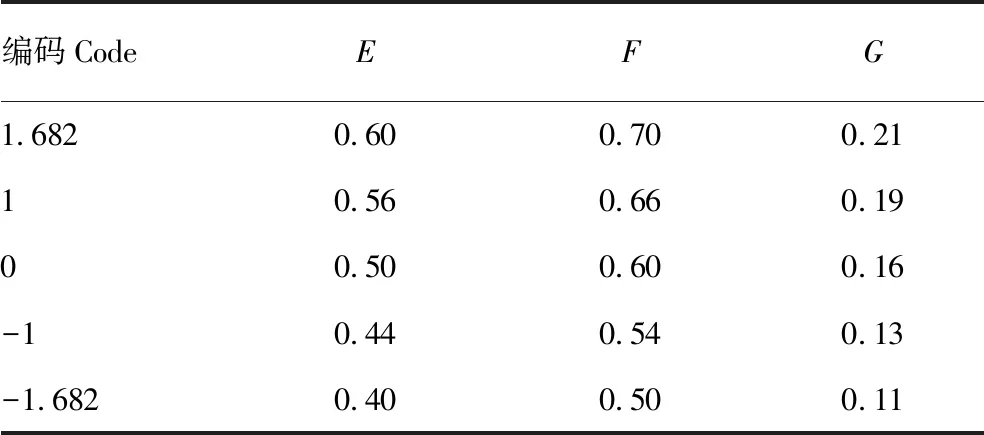
表6 中心组合试验因素水平编码
中心组合试验结果如表7所示,其中相对误差(δ)的计算方法与休止角的计算方法一致。应用软件Design Expert 8.0.6对试验结果进行分析,得到中心组合试验的回归模型。该回归模型的方差分析结果如表8所示,可以看出回归模型的P<0.000 1,说明滑动摩擦角的相对误差与所得回归方程关系是显著的;失拟项P=0.060 2>0.05,说明所得回归方程的非正常误差所占比例很小。该试验的相关系数(r)为0.979 0,因此所得回归方程可靠度较高。

表7 中心组合试验及结果
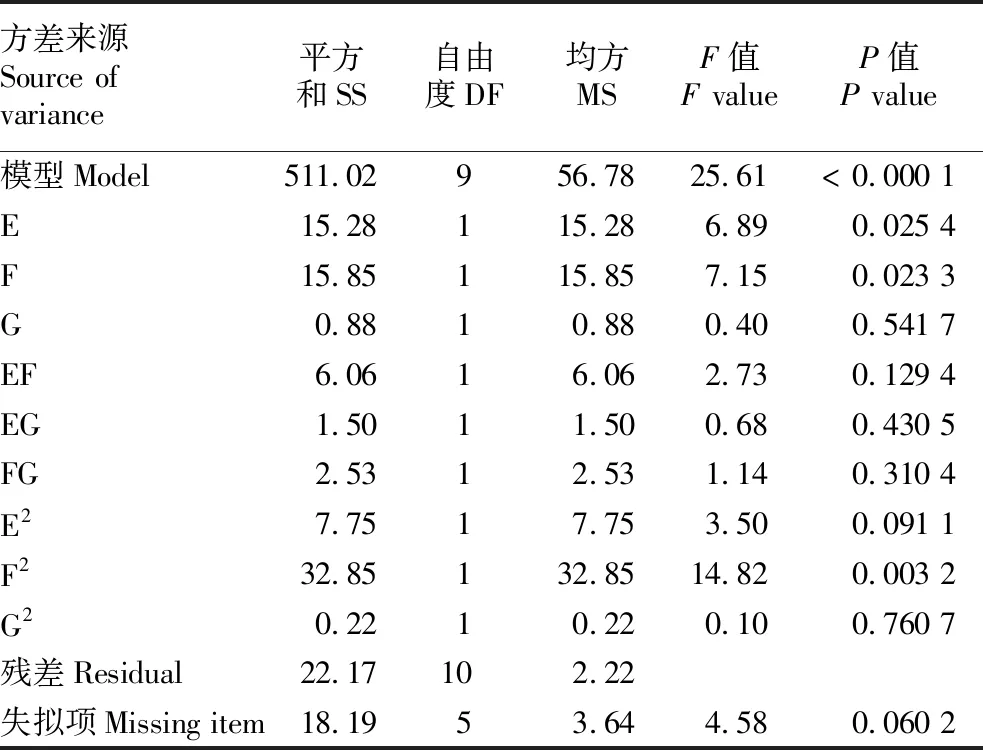
表8 中心组合试验回归模型方差分析
通过回归分析得到的误差回归方程为
δ=51.78+390.48E-423.97F+169.91G-241.67EF-240.28EG-312.50FG-206.44E2+425.06F2+138.24G2
应用Design Expert 8.0.6软件以滑动摩擦角的相对误差为目标对回归方程求解寻优,得到土壤与钢的相关系数(r)的最优值,土壤-65Mn钢恢复系数E为0.59,土壤-65Mn钢静摩擦系数F为0.67,土壤-65Mn钢动摩擦系数G为0.13。
3 验证试验
3.1 堆积角和滑动摩擦角验证试验通过Design Expert 8.0.6 软件对土壤的接触参数及土壤与65Mn钢的接触参数寻优,用最优结果进行仿真试验,通过5组重复的仿真试验,得到仿真值与实际值的对比,如表9所示。

表9 试验结果对比
将仿真结果与实际堆积结果进行对比,如图6所示,结果显示优化后土壤的仿真堆积角与实际堆积角的角度差距较小,表明该组仿真设置有一定的准确性。

图6 实际试验(a)和仿真试验(b)对比Fig.6 Comparison between actual test(a) and simulation test(b)
3.2 探针贯入验证试验为了进一步验证土壤参数的准确性,采用EDEM软件对探针贯入土壤过程进行仿真模拟,土壤颗粒半径仍设置为0.5~1.5 mm,土壤的接触模型为Hertz-Mindlin with JKR黏结模型,仿真参数设定以测量和标定结果为准,探针仿真模型采用SolidWorks软件创建的.x_t文件直接导入,土壤为直径80 mm、高150 mm的圆柱形,设置探针入土深度为100 mm,入土速度为8 mm/s,仿真时间为12.5 s,瑞丽时间步长为10%。在所测土壤参数和最优标定参数组合下的探针贯入1、5和10 cm的试验过程如图7所示。从图7可以看出,随着探针入土深度的增加,土壤扰动范围增大,与孙文峰等[22-24]的研究结果相似。因为探针尖头部分直径大于探杆直径,因此土壤扰动区域基本分布在探针尖头部分。

图7 探针贯入过程Fig.7 Probe penetration process
室内试验如图8所示,所用到的设备有万能试验机(DNS02-1KW)、探针(尖头最粗直径14 mm)、桶(直径80 mm,高度400 mm)。将含水率为(15±1)%的土壤装入桶内,装入深度为150 mm,不经过压实作用,体积密度约为1.15 g/cm3。利用万能试验机设置探针入土速度与仿真速度一致,在8 mm/s速度下贯入,贯入深度为100 mm,将探针的受力情况传到电脑存储,试验重复3次,分别记下探针入土深度为20、40、60、80和100 mm处的阻力值,最后取平均值为阻力值,试验结果见表10所示。由表10可知,随着探针入土深度的增加,探针阻力在逐渐增加,且仿真结果和室内试验结果的阻力增加幅度大致相同。

表10 贯入试验验证结果

图8 探针贯入室内试验Fig.8 Indoor test of probe penetration
4 结论
(1)针对土壤的本征参数(固体密度、弹性模量、剪切模量和泊松比),用体积置换法、直剪试验和土样压溃试验直接测量得到。
(2)针对土壤间的接触参数、表面能以及土壤与65Mn钢的接触参数,采用EDEM软件进行土壤堆积仿真模拟和土壤在65Mn钢板的滑落试验模拟。以堆积角和滑动摩擦角为指标,通过中心组合试验标定接触参数和表面能,获得土壤间的恢复系数0.28、静摩擦系数0.49、动摩擦系数0.24和表面能0.04 J/m2,土壤与65Mn钢的恢复系数0.59、静摩擦系数0.67、动摩擦系数0.13。
(3)为验证土壤参数的准确性,分别对土壤堆积角和滑动摩擦角的实际试验与仿真试验进行对比,得到两者相对误差分别为1.51%和2.73%。在所测参数和标定最优参数组合下进行了探针贯入试验的仿真模拟和室内试验,获得探针在贯入深度为20、40、60、80和100 mm处的阻力相对误差分别为8.59%、9.88%、9.72%、0.15%、6.98%,仿真试验与实际的探针贯入试验效果基本一致,证明了参数测量和标定方法的准确性。
