基于混合滤波的无人机抗干扰轨迹跟踪控制

张凯华,吴 磊,刘煜星,李一峰,黄阿强

(陕西送变电工程有限公司输电运检分公司,陕西 西安 710014)

0 引言

近年来,随着科学技术的快速发展,无人机得到越来越多的关注,被广泛应用于交通勘测、虚拟现实[1]和军事侦察等领域。为了避免无人机在工作过程中受强耦合性、外界环境和非线性等问题的干扰,关键就是对无人机抗干扰轨迹跟踪控制技术进行升级和优化[2]。

罗鼎馨等[3]在自适应智能滑模基础上构建自抗扰控制的双层轨迹跟踪控制模型,模型外层的终端控制系统采用自适应奇异滑模控制算法,可以保证无人机的飞行状态时刻达到收敛平衡,配合内层的方位控制模块完成无人机抗干扰的轨迹跟踪控制。但该方法没有消除强耦合性带来的干扰,导致轨迹控制效果较差。陈志明等[4]首先构建了位姿-双回路控制系统,以解决无人机的强耦合问题;然后采用自适应反步法作为无人机轨迹的回路跟踪模块,可以消除不确定干扰误差;最后设计轨迹控制模块,弱化外界干扰,完成无人机抗干扰轨迹的跟踪控制。但该方法没有构建无人机轨迹跟踪模型,导致跟踪误差较大。熊志豪等[5]在状态监测器的基础上融入快速跟踪控制策略,通过监测器在无人机的运动轨迹中判断其运动趋势,使用全局算法将控制策略与运动趋势相结合,完成无人机的抗干扰轨迹跟踪控制。该方法没有补偿不确定性干扰误差,应用过程中的抗干扰能力较差。

为了提升无人机抗干扰轨迹跟踪控制质量,本文提出基于混合滤波的无人机抗干扰轨迹跟踪控制方法。

1 轨迹跟踪与消除干扰

1.1 构建无人机轨迹跟踪模型

为了精准跟踪无人机运动轨迹,构建基于侧向偏差的无人机轨迹跟踪模型,具体步骤如下:

a.假设无人机保持同一高度匀速飞行,且飞行过程不受风向等外界环境因素的干扰,那么无人机的期望轨迹就是一条规律的直线或者曲线。根据轨迹航偏角与期望轨迹的方向,可以推导出无人机的部分轨迹跟踪模型为

(1)

h为无人机实际轨迹与期望轨迹之间的垂直距离;Uz为无人机的滚转舵偏角;α为航迹偏差角,是无人机速度方向与期望轨迹之间的夹角;cz为无人机的侧向过载;g为重力系数;β为无人机滚转角。

b.计算出无人机滚转舵偏角与滚转角之间的运动学传递函数[6],然后将传递函数投入到部分轨迹跟踪模型中,得到完整的无人机轨迹跟踪模型。

模型表达式为

(2)

Hβ为传递函数;o为无人机在飞行过程中的持续变量;J为无人机滚转传递系数;f(o)为中间变量;u为距离偏差;I为运动时间常数。

c.在无人机轨迹跟踪模型中,滚转舵偏角作为模型输入的控制变量,距离偏差值作为模型输出的控制变量,可以将o视为单独的非线性跟踪模块[7],实现无人机轨迹的实时跟踪,其数值的计算公式为

(3)

K为观测矩阵。

1.2 基于混合滤波的干扰消除

在构建的无人机轨迹跟踪模型中,消除强耦合性、非线性和外界环境等带来的干扰[8],可以提高轨迹跟踪的精度,具体步骤如下:

a.将跟踪的无人机运动轨迹视为由各节点组成的集合,在集合中根据强度差值赋予节点不同的权值,不同的权值对应着不同的能量。公式为

(4)

w为节点权值;n为节点权值的个数;Q为节点能量;i为轨迹节点;L为节点总数。

b.混合滤波算法使用的是混合粒子传播方式,其中一部分粒子通过分布函数[9]实现粒子的传播;另一部分粒子则是采用状态分散法完成粒子的传播。二者混合后可以保证轨迹分布在均匀的状态空间中,有效避免强耦合性、非线性和外界环境等带来的干扰对轨迹跟踪产生影响。分布矩阵与状态分散公式为:

(5)

a=al-1+l(bl-bl-1)

(6)

χ为分布函数;a、b为不同的无人机轨迹的状态参量;F为状态参量的维度;l为时刻。

c.根据分布函数与状态分散计算出l时刻下,混合滤波中粒子的状态参量al、节点能量Ql和轨迹节点对应的权值wl,计算式分别为:

(7)

(8)

(9)

i=1,2,…,O,O为无人机轨迹中的节点总数。

d.根据自适应容积卡尔曼滤波计算出无人机轨迹的状态估计值[10],输出l时刻抗干扰下的无人机轨迹,完成轨迹的跟踪与处理,公式为

(10)

2 轨迹控制

通过混合滤波消除跟踪轨迹的干扰后,采用串联终端滑模控制器,可以在有限时间内完成无人机轨迹的快速精准控制。

串联终端滑模控制器主要由位置控制模块与姿态控制模块串联组成,结构如图1所示。

图1 串联终端滑模控制器结构

2.1 位置控制

a.位置控制可以分为深度控制通道与水平控制通道[11],主要负责接收输入的控制参量。位置控制模块的工作状态为

vp+fp=[pqr]=[p′q′r′]

(11)

p、q、r分别为深度控制通道不同的控制输入参量;p′、q′、r′分别为水平控制通道不同的控制输入参量;vp为通道的总控制输入参量;fp为位置通道的扰动参量。

b.在位置控制模块工作状态中引入自动化模拟控制输入参量,公式为:

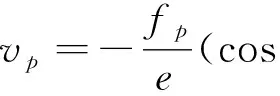
(12)

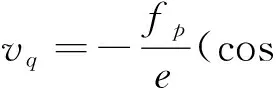
(13)

(14)

e为无人机质量;G为重力参数;vq、vr为不同的自动化模拟控制输入参量;α为航迹偏差角;ε为俯仰角。

c.以深度控制通道与水平控制通道的交接点为基准点,定义基准点处的控制误差[12],设计终端滑模的动态监测模块,公式为

(15)

Ep为水平位置处的控制误差参量;Sp为终端滑模参数。

d.得到终端滑模动态监测结果后,计算出水平控制通道和深度控制通道的隐藏控制动态方程,公式为:

(16)

(17)

φ为隐藏系数;φ为观测系数[13]。

e.计算出位置控制模块的总扰动参量f、输入参量的滚转角γ以及期望的俯仰角ε,完成无人机的位置控制,公式为:

(18)

(19)

(20)

2.2 姿态控制

a.位置控制模块输出的期望滚转角以及俯仰角信息成为姿态控制模块的工作指令,因此,可以根据输入参量的滚转角和俯仰角的期望值计算出姿态控制模块的控制策略[14],在该控制策略下隐藏系数φ、滚转角γ以及期望俯仰角ε的取值为:

(21)

(22)

(23)

Bφ、Bγ、Bε分别为隐藏系数φ、滚转角γ以及期望俯仰角ε的观测值。

b.为了利用姿态控制模块实现精准的、自动化的无人机轨迹控制,需要通过式(24)计算出姿态控制模块的控制动态角度参量[15]Sφ、Sγ与Sε,完成无人机的姿态控制。

(24)

3 实验与分析

为了验证基于混合滤波的无人机抗干扰轨迹跟踪控制方法的整体有效性,需要对其进行相关测试。将轨迹跟踪误差、轨迹控制效果和抗干扰能力作为评价指标,采用本文方法、文献[3]方法和文献[4]方法完成测试。

在Simulink中自主开发并搭建智能轨迹跟踪控制系统,如图2所示。

图2 智能轨迹跟踪控制系统

测试所使用的无人机如图3所示。

图3 测试使用的无人机

3.1 轨迹跟踪误差

将本文方法、文献[3]方法和文献[4]方法的跟踪结果与无人机的实际轨迹相比较,比较结果如表1所示。

表1 不同方法的轨迹跟踪误差

由表1可知,针对无人机运动轨迹的跟踪,本文方法的跟踪误差均小于文献[3]方法和文献[4]方法,并且随着实验次数的增加,跟踪误差比较稳定,说明本文方法的跟踪精度及其稳定性高。

3.2 轨迹控制效果

在三维坐标中,将本文方法、文献[3]方法与文献[4]方法控制后的无人机轨迹路径绘制出来,通过理想路径与控制后的路径相比较,得到不同方法的轨迹控制效果。不同方法的对比情况分别如图4～图6所示。

图4 本文方法轨迹

图5 文献[3]方法轨迹

图6 文献[4]方法轨迹

分析图4～图6可知,针对无人机轨迹的控制,本文方法控制后的轨迹与期望轨迹基本一致,说明本文方法的轨迹控制效果好。

3.3 抗干扰能力

为了验证各方法的抗干扰能力,将白噪声添加到无人机轨迹跟踪控制系统中,对比各方法跟踪的轨迹与期望轨迹。不同方法的抗干扰测试结果如图7所示。

图7 不同方法的抗干扰能力

分析图7可知,当无人机轨迹跟踪控制过程中受到噪声干扰后,本文方法跟踪的无人机轨迹与期望轨迹基本重合,说明本文方法的抗干扰性强。原因在于本文方法在对无人机轨迹跟踪后,采用混合滤波消除了不确定性干扰,进而在轨迹跟踪过程中不受噪声干扰,拥有更强的抗干扰能力。

4 结束语

无人机跟踪控制过程中容易受到强耦合性、非线性和外界环境等问题的干扰,导致无人机轨迹跟踪误差大、轨迹控制效果差及抗干扰能力弱等,为此以混合滤波为基础,设计无人机抗干扰轨迹跟踪控制方法。实验结果表明,本文方法的无人机轨迹跟踪误差较小、稳定性好,且抗干扰能力强。