基于FGM-SVR组合模型的港口吞吐量预测

邓 萍,刘淑龙

(1.重庆交通大学 交通运输学院,重庆 400074;2.重庆交通大学 经济与管理学院,重庆 400074)

0 引 言

港口作为综合交通运输枢纽,是经济社会发展的战略资源和重要支撑。而港口吞吐量是体现港口生产经营活动成果的重要数量指标。港口吞吐量预测在确定港口建设计划和生产计划方面都具有极其重要的作用。为此,有必要对港口吞吐量预测问题进行研究,以提出精度更高的预测港口吞吐量的方法,从而为政府和港口企业制定正确决策提供理论支持。

目前,国内外关于港口吞吐量预测的方法有很多,如BP神经网络[1-2]、时间序列分析法[3]、支持向量机(SVM)预测[4-5]、灰色预测[6-7]、组合预测[8-9]等。陈旭等[4]、宋长利等[5]利用改进的SVM模型对港口吞吐量进行预测;黄跃华等[6]提出基于正弦和具有自适应背景值的GM(1,1)优化模型,将其应用于港口吞吐量的预测;杜柏松等[7]建立了一种优化的灰色马尔科夫动态模型应用于港口吞吐量的预测;王振振等[8]在对数据进行加权灰色关联分析后,将三次指数平滑法与马尔科夫模型相组合对港口吞吐量进行了预测;柯桥等[9]将诱导有序加权几何平均算子赋权应用于基于改进的灰色模型和神经网络的组合预测模型进行三峡枢纽过坝货运量预测。由此看出,优化后的单个预测模型或者改进的组合模型更能提高港口吞吐量的预测效果。鉴于灰色预测模型中,相比整数阶累加GM(1,1)模型,分数阶累加GM(1,1)模型〔FGM(1,1)〕通过将分数阶累加代替整数阶累加,更能弱化原始数据序列的随机性,使灰色预测模型解的扰动性变小,实现最少信息的最大挖掘;SVM法基于结构风险最小化原理构造算法,在非线性小样本预测中表现较为领先,并且适应港口吞吐量非线性的特点。为充分利用各单项预测模型挖掘的数据信息,提高预测精度,笔者建立基于FGM(1,1)预测和支持向量回归(SVR)的组合预测模型进行港口吞吐量的预测。但是传统的组合预测模型存在赋权上的局限性,即通过计算确定各单一预测模型的权重来对组合预测模型进行赋权,各单项预测模型在各个时点上的权重不变。这种赋权方法没有兼顾各单项预测模型在各个时点上预测能力的强弱,从而会影响组合预测模型的预测精度[10-12]。为弥补这一缺陷,笔者将基于诱导有序加权平均(IOWA)算子的赋权方法应用于FGM(1,1)和SVR的组合预测模型,以误差平方和最小为准则建立新的组合预测模型对重庆港的港口吞吐量进行预测,并将预测结果与相同数据下FGM(1,1)和SVR各单项模型的预测结果进行比较。

1 模型理论

1.1 传统GM(1,1)预测模型

设港口历史货物吞吐量为:

X(0)={x(0)(1),x(0)(2),…,x(0)(j),…,x(0)(n)}

(1)

式中:x(0)(j)≥0,j=1,2,…,n。

对港口原始货物吞吐量进行一阶累加,得到序列X(0)的一次累加生成序列如式(2):

X(1)={x(1)(1),x(1)(2),…,x(1)(j),…,x(1)(n)}

(2)

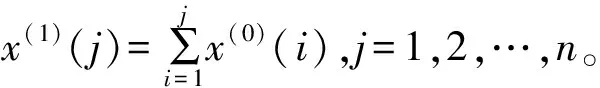
根据X(1)序列生成紧邻均值序列为:

Z(1)={z(1)(1),z(1)(2),…,z(1)(j),…,z(1)(n)}

(3)

式中:z(1)(j)=(1-λ)x(1)(j)+λx(1)(j-1),λ=0.5,j=2,3,…,n。

则传统GM(1,1)模型的基本形式为:

x(0)(j)+az(1)(j)=b

(4)

式中:a为发展系数;b为灰色作用量。

a、b均为待辨识参数,可根据最小二乘方法得到,因此传统GM(1,1)模型的白化方程为:

(5)

求解式(5),得到式(4)的时间响应公式为:

(6)

式中:j=1,2,…,n-1。

式(6)作一阶累减还原,最终还原式为:

(7)

式中:j=1,2,…,n。

1.2 FGM(1,1)预测模型

设港口原始吞吐量如式(1),原始序列X(0)的r阶累加生成序列如式(8):

X(r)={x(r)(1),x(r)(2),…,x(r)(n)},r∈R+

(8)

港口历史吞吐量序列X(0)的r阶灰色生成算子如式(9):

(9)

式中:j=1,2,…,n。

X(r)的紧邻均值生成序列为:

Z(r)={z(r)(1),z(r)(2),…,z(r)(j),…,z(r)(n)}^

(10)

式中:z(r)(j)=[x(r)(j)+x(r)(j-1)]/2,j=2,3,…,n。

则FGM(1,1)模型为:

x(r)(j)-x(r)(j-1)+cz(r)(j)=d

(11)

式中:c、d均为待辨识参数。

根据最小二乘法,可得FGM(1,1)模型参数满足式(12):

(12)

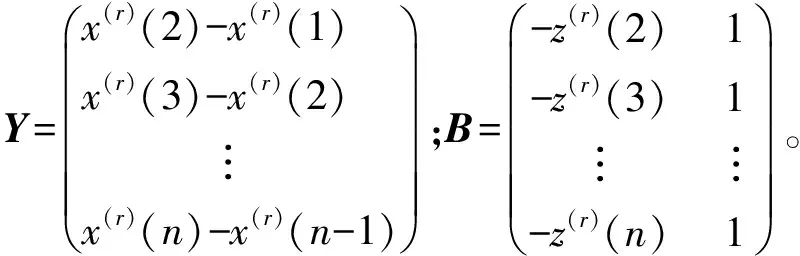
则FGM(1,1)模型的白化微分方程为:

(13)

求解式(13),得到时间响应式为:

j=1,2,…,n

(14)

j=2,3,…,n

(15)

1.3 支持向量回归

支持向量回归(support vector regression,SVR)是一种基于统计学习理论提出的机器学习方法,是在支持向量机(support vector machine,SVM)的基础上发展起来的回归问题。SVR是一种基于核函数的线性可分模型,可以将线性不可分的数据转化成高维空间的线性可分。SVR原理见图1。

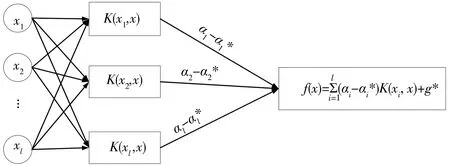
图1 SVR结构

对于训练样本D=[(x1,y1),(x2,y2),…,(xm,ym)],xi∈Rn为输入量,yi∈R为输出量,设在高维特征空间中建立的线性回归函数为:

f(x)=wφ(x)+g

(16)

式中:φ(x)为非线性映射函数;w为回归权重;g为阈值。则线性不敏感损失函数为:

L(f(x),y,ε)=

(17)

式中:f(x)为SVR预测值;y为真实值。

引入松弛变量ξi、ξ*,则SVR的目标函数与约束条件分别如式(18)、式(19):

(18)

(19)

式中:C为惩罚因子,C越大表示对训练误差大于ε的样本惩罚越大;ε规定了回归函数的误差要求,ε越小表示回归函数的误差越小。

则回归问题转化成求待定参数的凸二次规划问题,利用对偶原理及拉格朗日函数将原问题转化对偶形式为:

max(α,α*)=

(20)

(21)

式中:K(xi,xj)=φ(xi)φ(xj)为核函数。通过引入核函数解决维数问题,可在不知映射函数的情况下实现回归估计。

常用的核函数有多项式核函数、张量积核函数、高斯径向基函数等,使用高斯径向基函数(RBF)将核函数代入式(20)得到SVR的非线性回归函数,如式(22):

(22)

1.4 基于IOWA算子的组合预测模型

根据IOWA算子[13]赋权原理,以单项预测模型预测精度为诱导值对单项模型进行有序赋权,在某时点预测精度高的单项模型将被赋予较大权重,预测精度低的单项模型将被赋予较小权重。组合模型建立流程见图2。

图2 组合模型建立流程

设第i种单项预测模型在t时期的预测精度为ait,则表示为:

(23)

式中:ait∈[0,1];xt为实际值。将ait看作预测值vit的诱导值,则n种单项预测方法的预测精度与其对应的预测值就构成了n个二维数组{(a1t,v1t),(a2t,v2t),…,(ant,vnt)}。

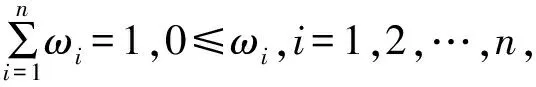
(24)

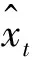
(25)

(26)

2 模型验证与评价

以重庆港2005—2020年港口吞吐量为样本数据(表1),分别建立FGM(1,1)和SVR各单项预测模型和基于IOWA算子的组合预测模型对港口吞吐量进行预测与分析。将2005—2017年样本数据作为建模数据,2018—2020年样本数据作为预测模型验证数据,并对重庆港2021—2024年港口吞吐量进行预测。

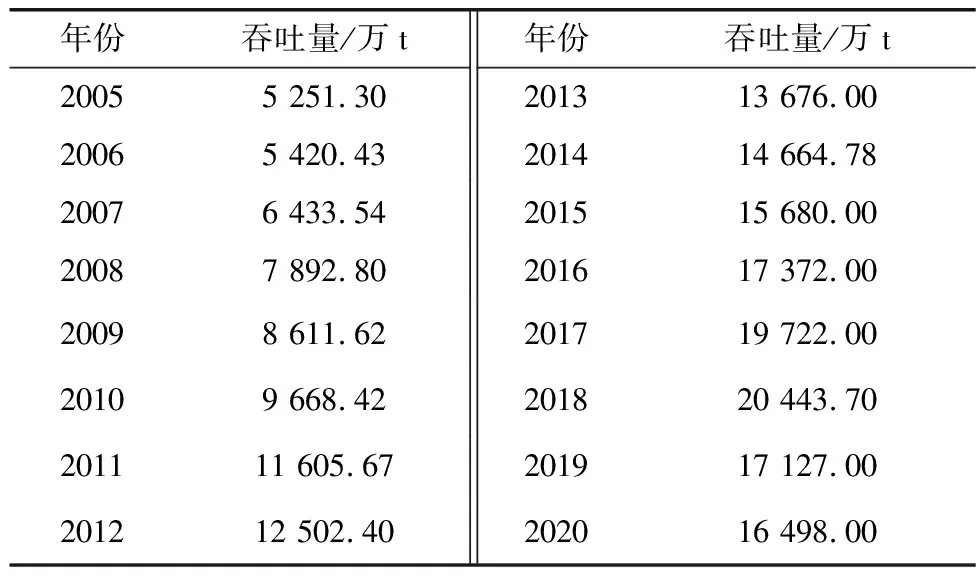
表1 2005—2020年重庆港港口吞吐量

2.1 FGM(1,1)模型的港口吞吐量预测结果分析

以表1的样本数据为原始数据,按照上述建模过程,利用Anaconda中的Spyder对原始数据分别进行传统GM(1,1)和FGM(1,1)模型求解。在分数阶累加灰色预测模型预测中,当r=0.3时,r∈[0,0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1.0],模型的平均绝对百分比误差(EMAP)最小,如式(27):

(27)

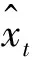
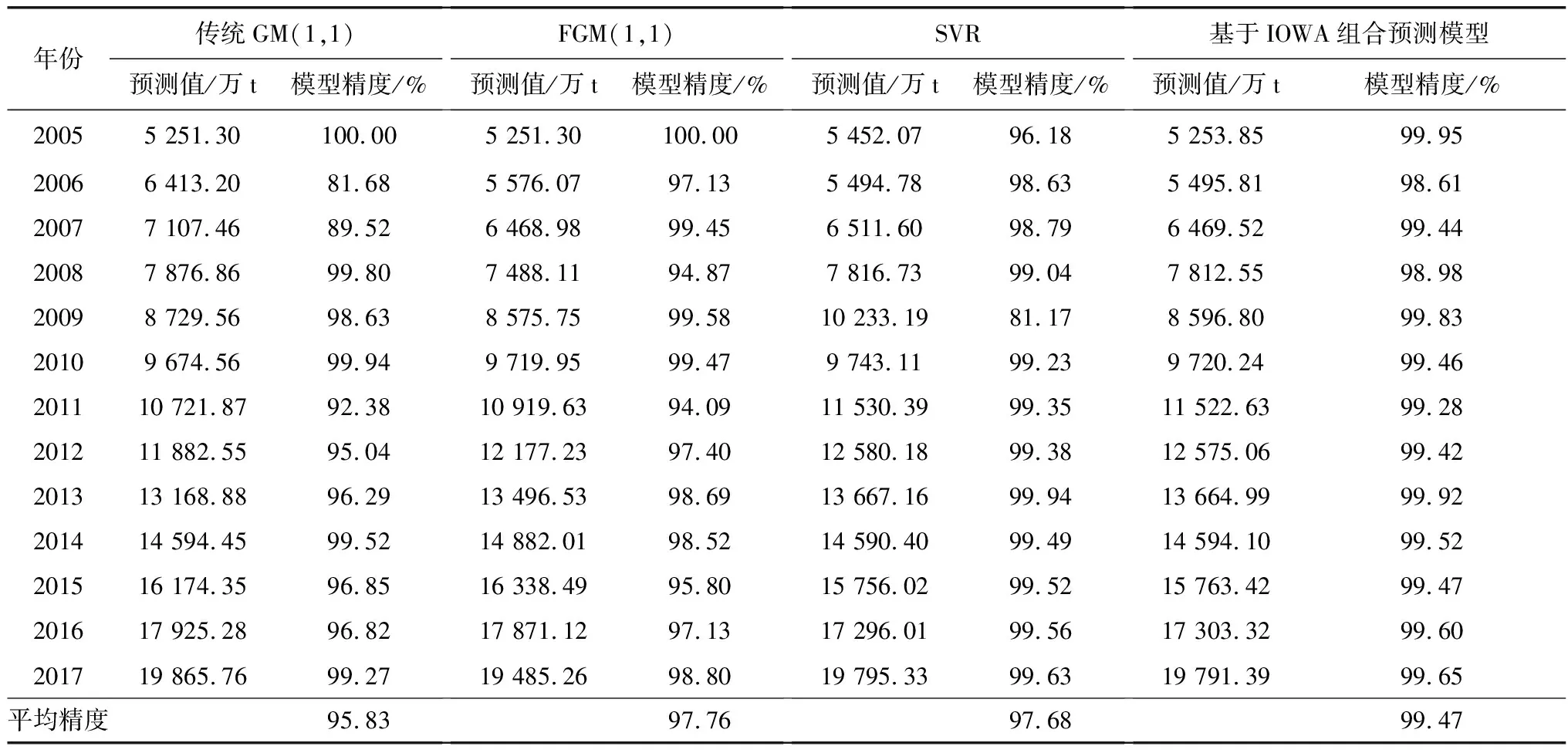
表2 2005—2017年各模型预测数据比较

2.2 SVR模型的港口吞吐量预测结果分析

支持向量回归模型的求解最终转化为一个带约束的二次规划问题,笔者利用libsvm软件包中的函数svmtrain实现SVR回归模型的训练与创建。主要预测过程为:

1)产生训练集和测试集。为了满足libsvm软件包相关函数调用格式的要求,产生的训练集和测试集应进行相应的转换。

2)利用libsvm软件包中的svmtrain函数实现对SVR回归模型的创建和训练。并综合衡量归一化、核函数的类型以及参数的取值对回归模型的性能影响程度展开设计。

3)利用libsvm软件包中的svmpredict函数实现对SVR回归模型的仿真测试,返回的第1个参数为对应的预测值,第2个参数中记录了测试集的均方误差E和决定系数R2。

4)利用svmpredict函数返回的均方误差E和决定系数R2,对所建立的SVR回归模型的性能进行评价。若性能没有达到要求,则可以通过修改模型参数、核函数类型等方法重新建立回归模型,直到满足要求为止。

传统的运用SVR预测模型预测港口吞吐量除了吞吐量样本数据作为输入指标外,一般只考虑了时间。但是后续研究发现[4],将港口吞吐量影响因素和吞吐量样本数据同时作为输入指标更能提高模型的预测精度。因此,为了更好地发挥SVR预测模型的预测效果,笔者将港口吞吐量影响因素和吞吐量样本数据同时作为输入指标来预测重庆港口吞吐量。影响港口吞吐量的因素较为复杂,通常受到港口所在地区经济与贸易发展水平、港口自身基础设施条件以及所在地区货运量需求等因素的影响。选取国内生产总值(GDP)、进出口贸易总额、固定投资总增长情况、社会消费品零售总额、常住人口总量、城市化率、港口堆场总面积、生产用港口码头泊位数、公路货运量、铁路货运量共10个影响因素指标(表3)和重庆港2005—2020年港口吞吐量作为SVR模型预测过程中的输入指标。由此构建的SVR模型预测结果见表2,SVR模型港口吞吐量平均预测精度为97.68%。

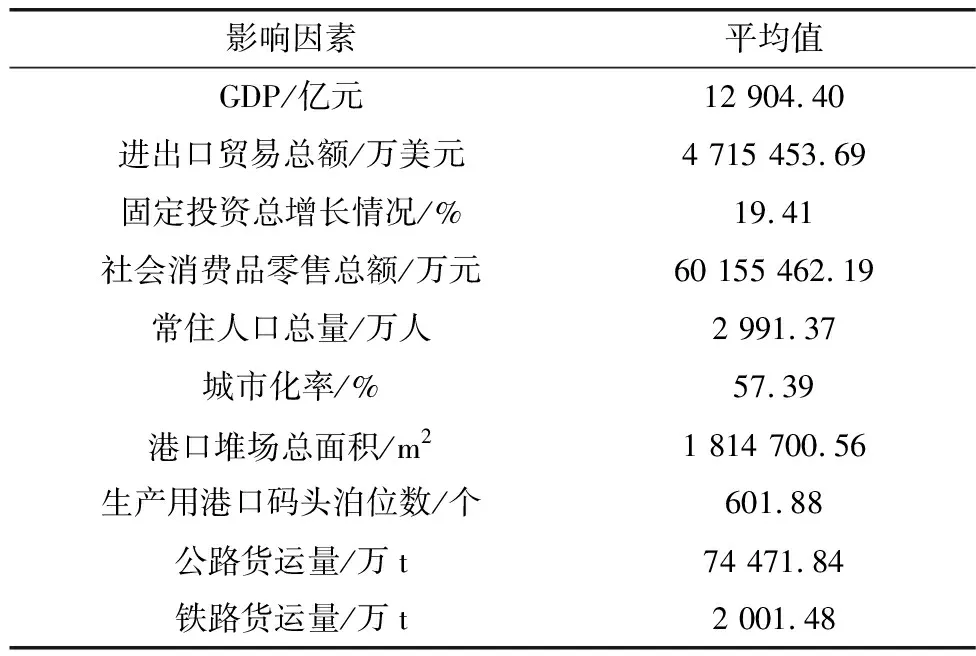
表3 港口吞吐量影响因素指标

2.3 基于IOWA算子的组合预测模型预测结果分析

根据式(25)与表2计算得出基于IOWA算子的组合模型预测值,由FGM(1,1)与SVR模型的预测值可得组合模型预测值为:

(28)

同理,可求得其他年份基于IOWA算子的组合模型预测值。将式(28)代入到式(25),运用lingo软件求解,求得ω1=0.987 3,ω2=0.012 7。组合模型预测平均精度为99.47%(表2),较FGM(1,1)、SVR模型预测精度分别提高了1.71%、1.79%。

为验证基于IOWA算子组合预测模型比FGM(1,1)和SVR各单项预测模型预测效果更好,先假设2018—2020年重庆港港口吞吐量实际数据未知,然后根据组合模型预测特征,在预测未来时刻n+1,n+2,…,n+k时,第i种单项模型预测精度qi可用式(29)计算:

(29)

式中:qit表示第i种预测方法在t时刻的预测精度。

根据式(29)分别计算出单项预测模型FGM(1,1)和SVR在2018—2020年各年的预测精度,最后再利用最优组合权重ω1=0.987 3,ω2=0.012 7以及各单项模型的预测值计算求得基于IOWA组合预测模型2018—2020年的港口吞吐量预测值,见表4。

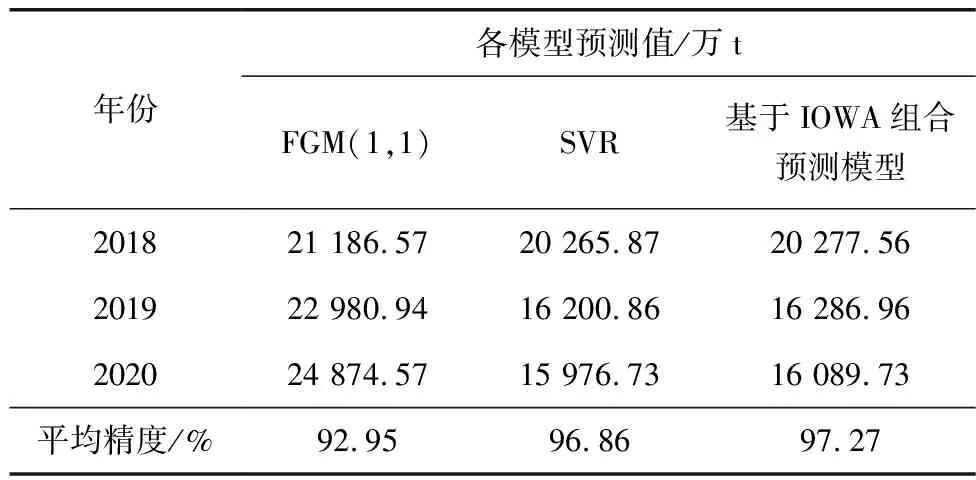
表4 2018—2020年各模型预测数据比较

由表4可知,基于IOWA算子的组合预测模型比各单项预测模型FGM(1,1)和SVR预测效果更优。

2.4 预测精度比较分析

分析预测结果可知,基于IOWA算子的组合预测模型比FGM(1,1)和SVR各单项模型预测精度更高。FGM(1,1)和SVR两种单项预测模型和基于IOWA算子的组合模型的预测值与实际值对比见图3。

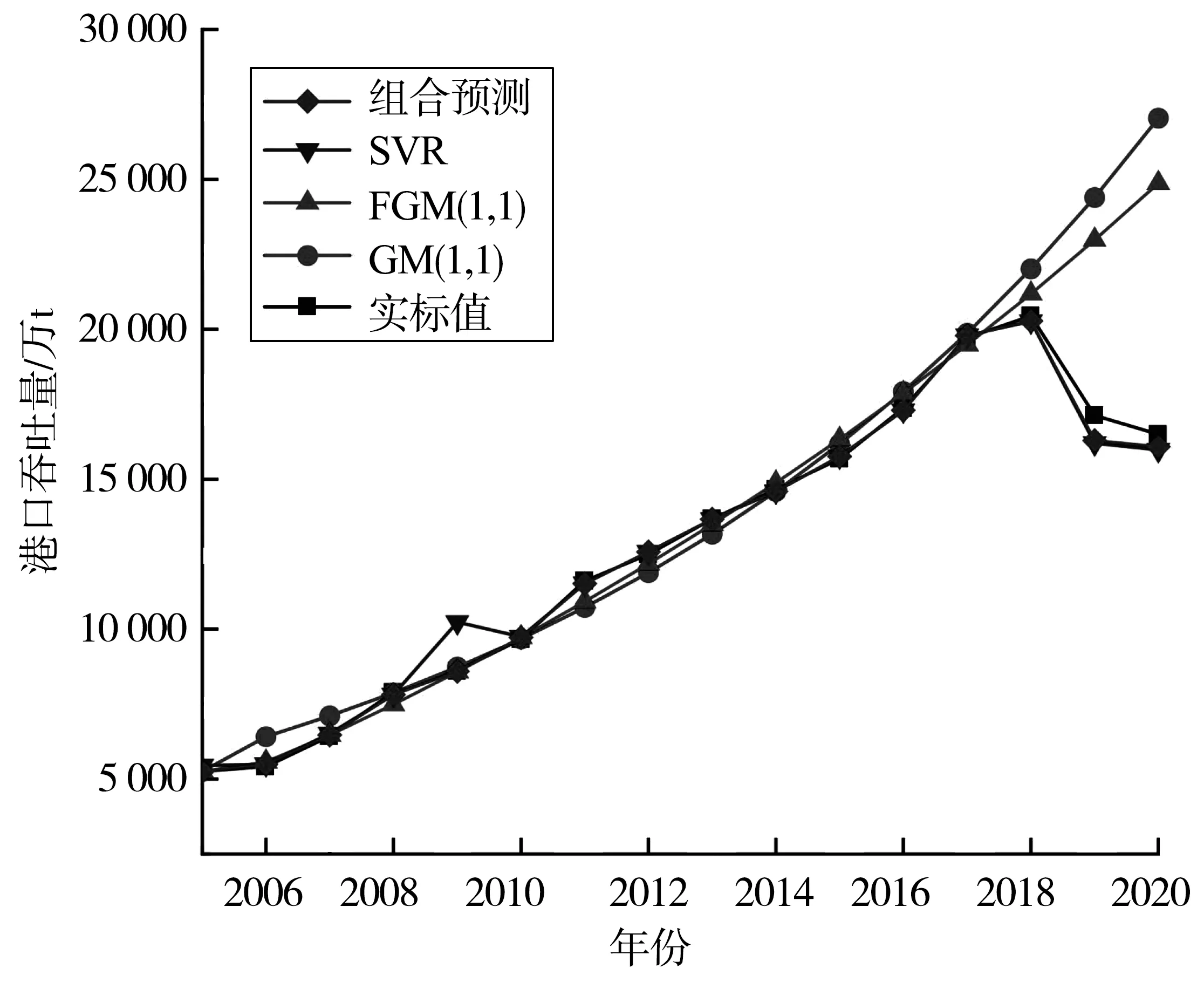
图3 单项预测与组合模型预测结果对比

由图3知,基于IOWA算子的组合预测模型预测值与实际值拟合度更高,预测值更接近实际值,这充分说明组合预测模型预测的精度要优于各单项预测模型,能够更好的反映数据自身特征。基于IOWA算子的组合预测模型在2018—2020年预测值平均精度为97.27%,相较于FGM(1,1)模型平均预测精度提高了4.32%,相较于SVR模型平均预测精度提高了0.41%。

为了进一步说明组合预测模型优于单项预测模型,选取均方根误差ERMS、平均绝对误差EMA和平均绝对百分比误差EMAP对单一预测模型预测值和组合预测模型预测值进行检验,其计算公式如式(30):

(30)

ERMS、EMA、EMAP计算结果见表5。由表5可知,基于IOWA组合预测模型的均方根误差、平均绝对误差和平均绝对百分比误差均明显优于各单一预测模型,由此证明了组合预测方法的有效性。

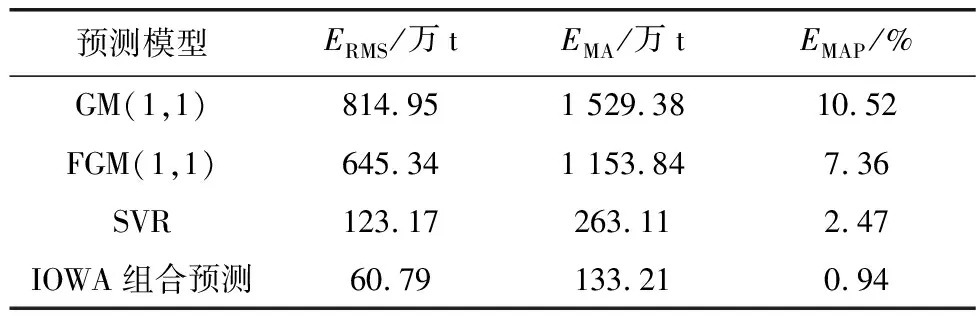
表5 误差检验

2.5 2021—2024年港口吞吐量预测

运用重庆港2005—2020年港口吞吐量实际值,通过FGM(1,1)和SVR各单项预测模型以及基于IOWA算子的组合预测模型预测得到重庆港2021—2024年港口吞吐量的预测值(表6),以供未来参考。

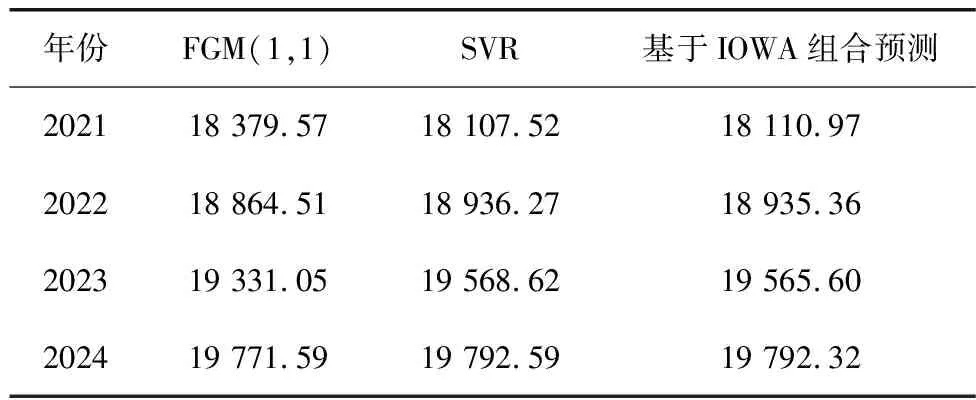
表6 2021—2024年各模型港口吞吐量预测值

3 结 语

鉴于灰色预测和支持向量机方法在港口吞吐量预测方面具有的优势,笔者提出建立FGM(1,1)和SVR的组合预测模型,针对传统组合预测模型在赋权上的局限性,提出基于IOWA算子赋权的新的组合预测模型。经实例分析表明,模型FGM(1,1)和SVR均可以很好地拟合重庆港港口吞吐量,但是基于IOWA算子的FGM-SVR新的组合预测模型比各单项预测模型的预测效果更优,预测精度更高。该新的组合预测模型是有效的,能够较好地结合FGM(1,1)和SVR这两种单一预测模型,为港口吞吐量预测提供一种新的方法。