非额定工况实船试验确定消滩水力指标的方法

许光祥,王松宁,王舒涛,蔡 创

(1.重庆交通大学 河海学院,重庆 400074;2.澜沧江244界碑至临沧港四级航道建设指挥部,云南 景洪 666100 )

0 引 言

急滩在山区航道中普遍存在,坡陡流急是急滩碍航的主要特征。在急滩整治设计中,依据的标准除航道尺度、设计水位等参数外,还有一个重要的标准——消滩水力指标(以下简称“消滩指标”)。一般消滩指标是指某船舶在额定功率和额定载重工况下能自航上滩的最大航线流速和比降,体现为多组成对的流速和比降组合,简称为坡流指标[1]。由此可见,消滩指标体现了某船舶的上滩能力,急滩整治后,通过滩段的流速和比降与消滩指标的对比,可体现航道工程的整治效果。

实船上滩试验是确定消滩指标的方法之一[1-2]。一般理解为:当某船舶在额定载重情况下,以额定主机功率上滩航行时,其航速刚好为上滩要求的最小航速(一般取0.3～0.5 m/s),此时滩段的流速和比降(可适当考虑安全储备)便为一组坡流消滩指标。然而,山区航道通航环境复杂,受众多因素的影响,实船上滩试验难以满足额定工况条件。如滩段流速比降过大,船舶满载难以上滩,常减载航行,此时便出现非额定载重工况;如滩段整治后流速比降大幅减小,船舶上滩航速明显大于要求的最小航速,此时出现非额定航速工况,或没有满负荷运行也能上滩,便出现非额定功率工况;或上述3种情况都存在,属于典型的非额定工况上滩航行。总之,出现非额定工况下的实船上滩航行时,滩段的流速比降便不是真实的消滩指标,由此便提出一个问题,如何科学合理的将非额定工况的滩段流速比降转换为额定工况下的坡流指标[2]。笔者针对此问题,依据实船试验测试成果,通过一定的理论和统计相关分析,提出实用的转换方法。

1 典型额定工况的消滩指标确定

1.1 理想额定工况

实船上滩试验确定消滩指标,比较理想的工况是全额定工况,即船舶在额定载重、额定主机功率上滩航行时,其航速刚好为上滩要求的最小航速。由此可看出,额定工况需要满足3个条件,即:①S=S0;②P=P0;③Va=Vamin。

式中:S、P分别为体积排水量和主机功率,m3、kW;S0、P0分别为额定体积排水量和额定主机功率,m3、kW;Va为对岸航速,m/s;Vamin为船舶上滩要求的最小对岸航速,一般取Vamin=0.3～0.5 m/s[3]。

设试验滩段流速、比降分别为Ut、Jt,考虑一定安全储备,那坡流消滩指标U、J便为:

(1)

式中:αU为流速系数修正,一般取αU=1.15～1.30;αJ为考虑船舶上滩时水面比降局部增大的修正系数,一般取αJ=1.1～1.2。

1.2 额定载重额定功率工况

当船舶以额定载重额定功率上滩航行时,其上滩航速Va不等于要求的最小航速Vamin。此种情况的指标转换较为简单,可采用对水航速等效的方法确定流速指标,即:

Ut+Va=U+Vamin

(2)

考虑一定安全储备后,坡流消滩指标U、J应为:

(3)

可以看出,当Va=Vamin时,式(3)与式(1)完全相同。

2 非额定工况的消滩指标确定

针对普遍情况,理想额定工况的3个条件均不满足,属于典型的非额定工况,此时消滩指标需要采用半经验半理论方法进行转换确定。通常情况下,消滩指标是通过船舶推力和阻力平衡条件计算确定的[4-5]。非额定工况实船试验确定消滩指标一般也需要借助这个平衡条件,只是依据试验资料可以使计算结果更为接近实际,同时可以将水流阻力计算进行简化,以避开不确定的水流阻力。

对于实船上滩试验,由于各个航段的航道宽窄深浅、水流大小和比降陡缓不同,航行姿态多变,船舶不仅难以保持匀速直线运动,且还存在转弯、横移等现象,要简单准确地描述各种受力特征十分困难。但可从总体统计的角度出发,把船舶视作单质点直线航行,船舶受力状态总体上可描述为:

Fe=RV+RJ+Fg

(4)

式中:Fe为船舶有效推力,kN,简称船舶推力。

通常采用推进系数简化方法计算:

(5)

式中:e为推进系数,是实际推进船舶前进的功率与主机功率的比值;P为主机功率,kW;Vs为对水航速,m/s,Vs=Ut+Va。

RV为船舶航行的水流阻力,kN,对某具体船舶,一般为对水航速Vs的函数,可表述为RV(Vs),山区河流通常采用兹万科夫法计算[4]。RJ为船舶航行的坡降阻力,kN,相当于船舶排水重量在航线方向的分力:

RJ=αJρgSJ

(6)

式中:ρ为水密度,t/m3;g为重力加速度,g=9.81 m/s3。

Fg为船舶非匀速航行产生的惯性力,kN,采用式(7)计算:

(7)

式中:a为船舶航行加速度,m/s2;ΔVs为Δt时间内的船舶航速差,由实船试验各测点航速资料获取。

于是实船上滩受力状态可表达为:

(8)

消滩指标中的流速和比降两个指标一般只能转换一个指标,需要固定其中一个指标,鉴于坡降阻力影响因素较为明确,通常固定比降J,并取J=Jt/αJ。另外,用于确定额定工况的消滩指标,通常假定推力和航行阻力平衡,即Fg=0。由此,对于额定工况,同样有上式的平衡方程,只需将各变量变为的额定工况的参数(下标添加“0”为标记):

(9)

根据式(8)和式(9)有:

(10)

式中:Vs、P、S、J、ΔVs、Δt等分别为实船试验测试的已知值;P0、S0分别为船舶固有的额定参数;水流阻力RV可选用一个阻力计算公式进行计算,如兹万科夫公式等进行计算;推进系数e、e0取值相对比较复杂,在缺乏具体试验资料时,可取固定值,如川江(长江上游河段)取0.38[4],澜沧江五级航道时取0.41[2,6]。为此,式(10)便只有一个未知数Vs0,通过试算获取其值后,按式(11)得到坡流消滩指标:

(11)

由此可见,采用水流阻力RV不同的计算公式,可以获得不同的计算结果。

2.1 兹万科夫阻力公式法

我国山区航道水流阻力计算常采用兹万科夫公式,对于机动船,公式为:

(12)

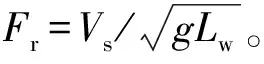
将式(12)试验工况的RV(Vs)以及额定工况的RV(Vs0)代入式(10),再通过试算便可求解出Vs0,继而获得坡流指标。文献[7-9]指出,不同的河道应用兹万科夫方法确定的水流阻力需要一定修正,不然会造成一定偏差,文献[7]根据静水航速试验成果给出了澜沧江机动船的阻力修正函数。由于式(10)采用了额定工况与实际工况水流阻力的对比形式,在一定程度上消除或削弱了水流阻力计算引起的偏差,相当于通过实船试验对水流阻力进行了适当修正,体现出了实船试验的作用。

2.2 通用阻力公式法

兹万科夫阻力公式法虽然比较严谨,但计算较为繁琐,涉及的参数较多,宜适当进行简化。如果水流阻力RV采用通用的公式[10]:

(13)

式中:CD为考虑摩擦、粘压及兴波阻力等影响的综合水流阻力系数。

那对于额定工况,同样应有:

(14)

代入式(10)有:

(15)

整理得:

(16)

由于综合阻力系数CD影响因素复杂,计算十分繁琐,且计算公式众多。在Vs与Vs0差异不大的情况下,可以假定CD=CD0,以消除并避开对CD的计算,则上式可变为计算较为简便的公式:

(17)

式(17)同样只有一个未知数Vs0,通过试算获取其值后,再按式(11)计算坡流消滩指标。

2.3 修正通用阻力公式法

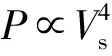
(18)

2.4 适用范围

考虑到兹万科夫船阻力公式适合于内河山区航道,同时推荐的修正通用阻力公式资料来源于澜沧江实船试验,所以转换公式适用范围之一是山区航道。另外,采用了对比法避开了阻力系数CD的计算,由于影响CD的主要因子是船舶傅汝德数Fr,所以转换公式适用条件之二是实船试验和消滩指标的Fr相差不宜过大。

3 应用与实践

3.1 实船静水航速试验

在澜沧江四级航道工程建设期间,选用港龙自卸运输02船(500 t级货船)进行了实船静水航速试验,其船型主要参数见表1。试验水域确定在澜沧江景洪水库库区思茅港下游约3 km的象鼻山～大干河口库区段,该河段水面直线长度约2.5 km,宽度270～380 m,水深达18～25 m,库面流速大部小于0.3 m/s,局部稍大也不到0.4 m/s。加之左右两岸被高山遮挡,风力等级较低,是理想的静水航速试验水域。试验过程全程监测航迹线(航速由航迹线算取)、主机转速等航行参数,取航速稳定时段进行统计分析,再通过上、下行航速的平均以消除流速的影响,试验成果汇总于表2。

表1 试验船主要船型参数(额定参数)

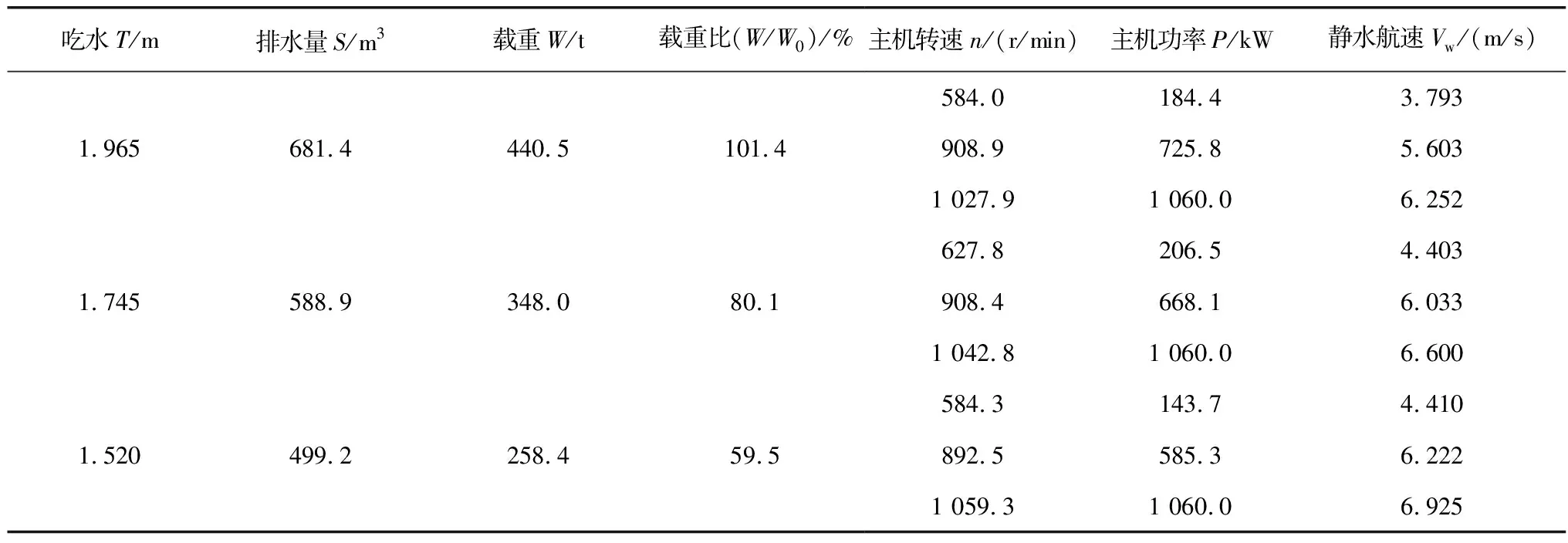
表2 静水航速试验结果汇总

通过相关分析,试验船静水航速可采用式(19)估算,可以看出主机功率与航速之间存在4次方而不是3次方关系以及额定工况下试验船的静水航速为6.15 m/s。

(19)

3.2 实船上滩试验

在澜沧江四级航道工程建设期间对港龙自卸运输02船也进行了实船上滩试验。试验河段安排在景洪至243界碑段,并选择勐宋滩、无名滩、梭罗滩、南班河口滩、贺宽下滩、贺宽上滩等6个急滩作为上滩试验的重点滩段。行使过程中全程监测航迹线、主机转速、舵角等航行参数,在行使到重点滩险前、后1小时内施测滩段流速和比降。受装载条件限制,同时考虑到航行安全,试验时未满载,载重比约88.7%,具体见表3。

表3 试验船主要船型参数(试验时参数)

试验时测试间隔时间为1 s,成绩处理时采用的时间间隔为10 s,考虑到测试数据点较多,不宜一一罗列,将其主要成果以图的形式展现,见图1。其中比降J为航迹线比降,U为航线船体范围内平均流速。从图1可以看出,各参数沿程均不稳定,航行基本不处于平衡状态。同时,每个滩段的最小航速均不小于0.3～0.5 m/s,同时其对应的主机功率也远不到满负荷1 060 kW,属于典型的非额定工况。

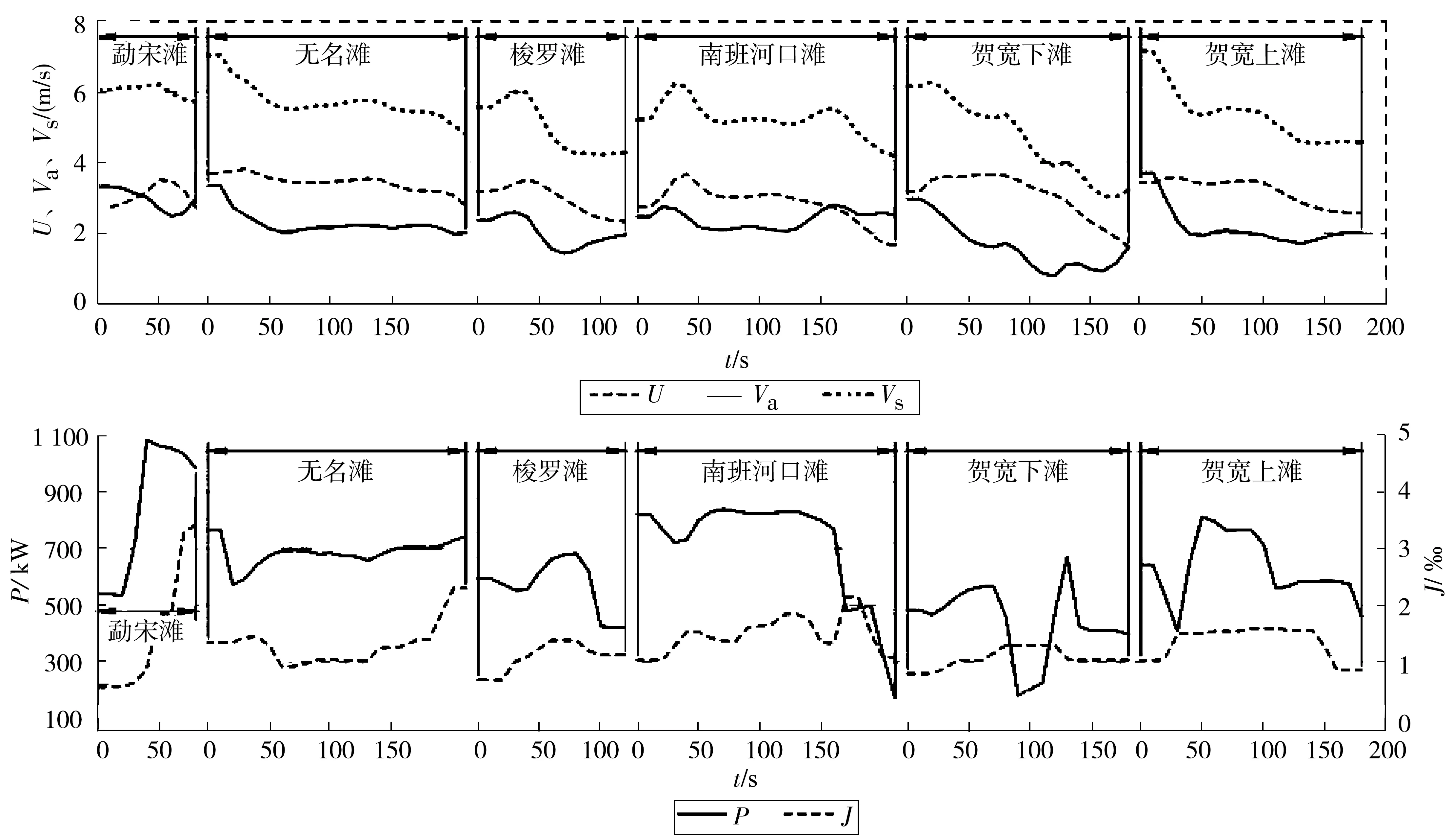
图1 实船上滩试验测试成果

依据实船试验测试成果,通过一定的理论分析计算,得到了试验船推进系数的计算式(20),从图2可以看出,e随似进速系数JP呈现抛物线关系,约在JP=0.69左右出现最大值,约0.405[12]。

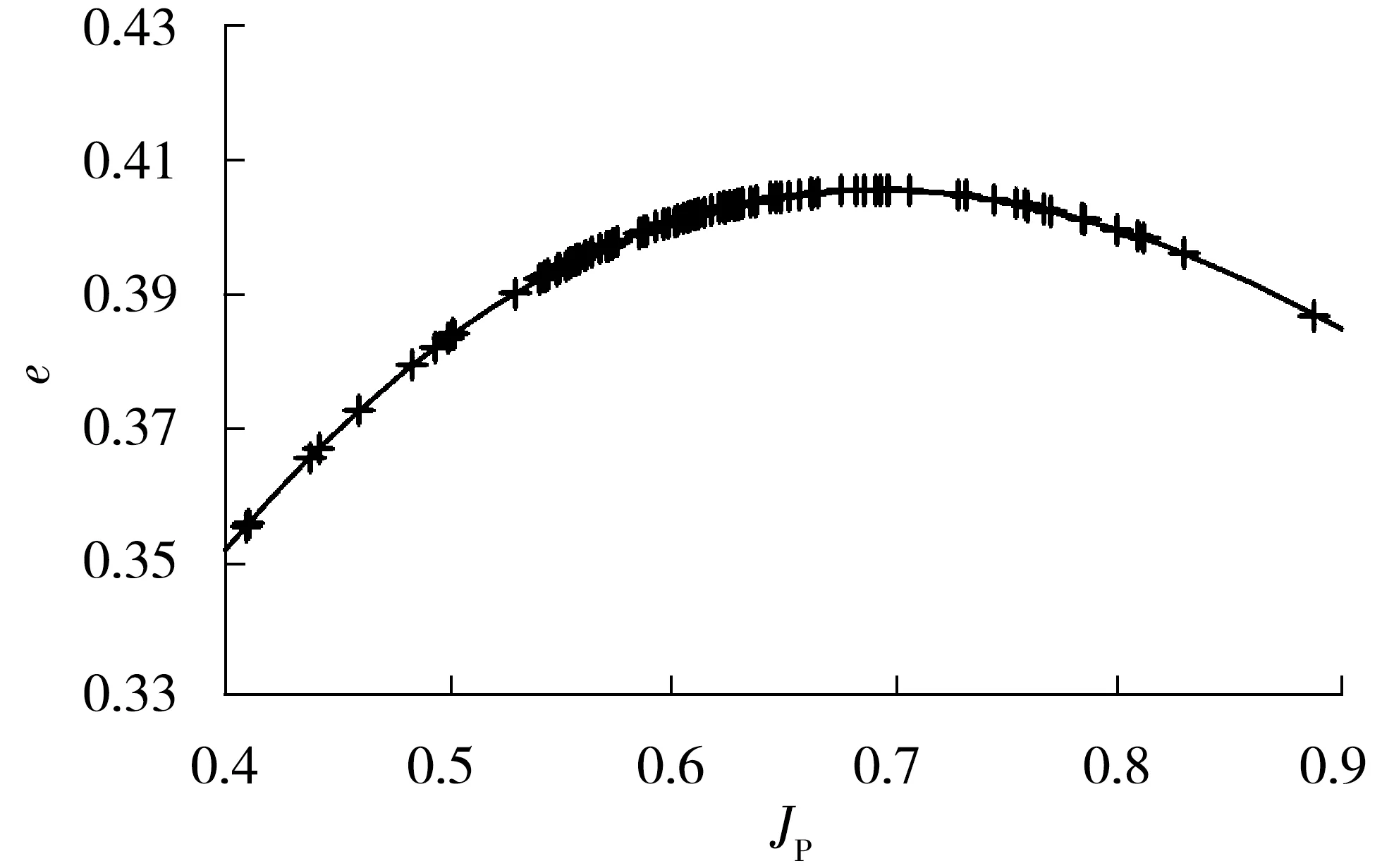
图2 推进系数e变化曲线

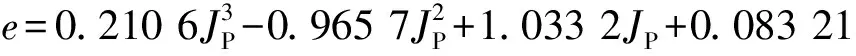
(20)

式中:JP=Vs/P1/3,称为似进速系数。

3.3 额定工况Vs0的转换

选取的参数aU=1.15,aJ=1.15,Vamin=0.3 m/s,首先应用修正通用阻力公式法式(18)将实船上滩试验实际工况的Vs转换为额定工况的Vs0,图3为转换前后的对比。可以看出,转换前后的测点都比较散乱,难以直接获取坡流指标。主要原因是上滩试验不处于匀速直线运动的平衡状态,采用简单的平衡分析方法只是尽量消除偏差,同时测量存在一定偏差,出现一些不真实的测点。因此需要依据坡流指标存在的内在关系,并去掉不真实的测点,然后从总体统计的角度出发获取坡流指标。

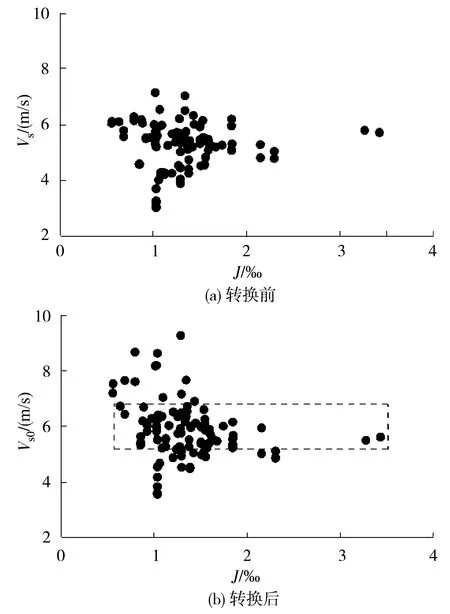
图3 转换前后的对水航速与比降的关系

根据式(19)可以算出上滩试验各测点对应功率的静水航速Vw,由于上滩水流存在水面比降,同功率的对水航速应该小于静水航速,理应存在Vw/Vs>1,考虑到测量误差,可适当放宽。从图4的Vs0随相对航速比Vw/Vs的变化关系看,明显呈现三段不同的变化规律。可以分析出,Vs0<5.2 m/s的Vw/Vs过大,Vs0>6.8 m/s的Vw/Vs过小,比较合理的测点应该在Vs0=5.2～6.8 m/s的范围内(图4虚框内)。

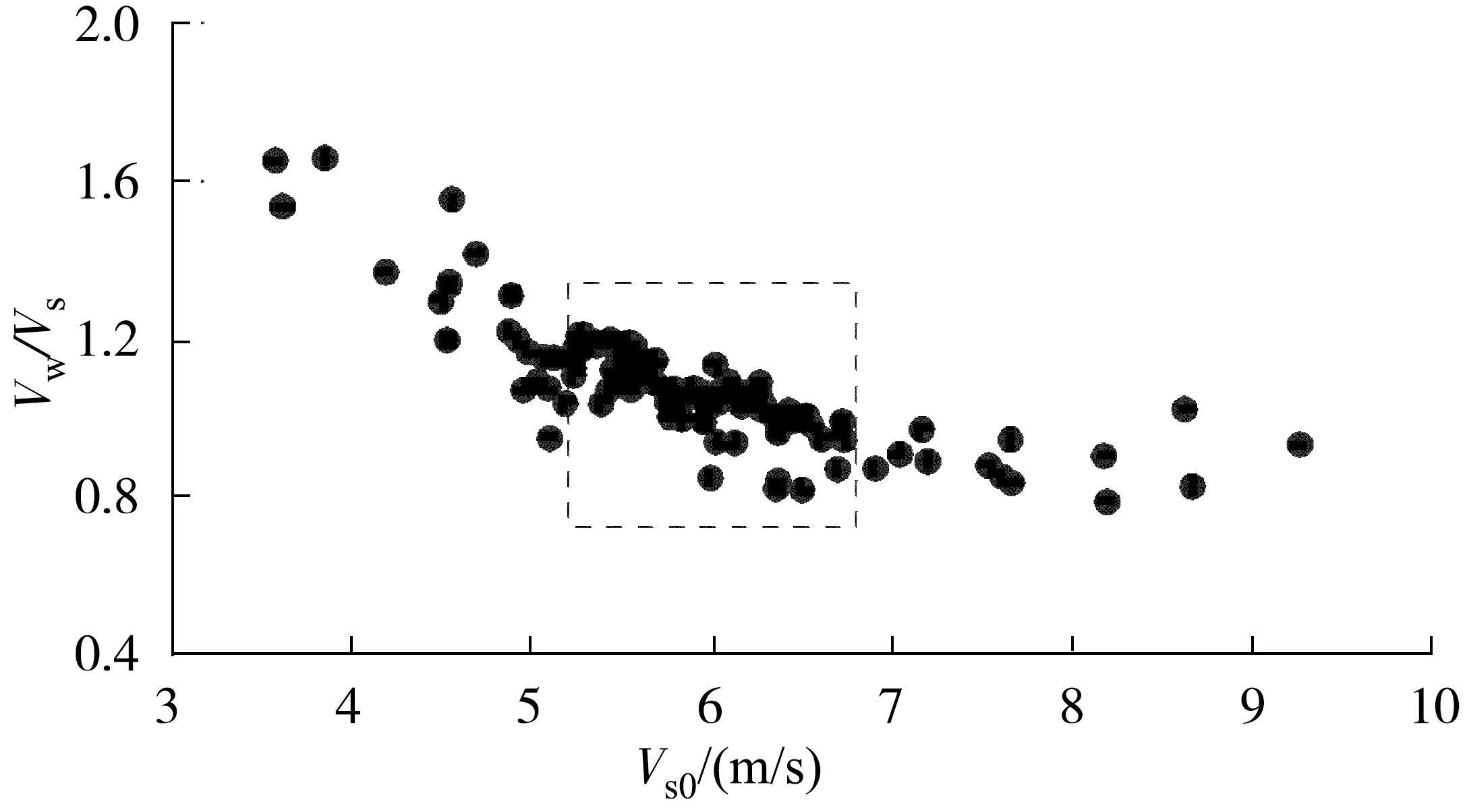
图4 测点合理性检验

虽然确定了测点选定的范围,但Vs0与J的关系仍不十分明确(图3(b)的虚框内),因此需要应用坡流指标存在的内在关系进行拟合。根据已有研究成果[2,12,13],坡流指标的U、J存在如下关系:

(21)

式中:EC为综合消滩指标,可理解为船舶主机提供的单位能量;U2/(2g)则为船舶航行水流阻力消耗的单位动能;λLJ为λ倍船长L范围内船舶重力分量消耗的单位势能,两项耗能之和U2/(2g)+λLJ与主机提供的单位能量EC达到平衡,便构成了消滩指标的内在关系。

由此,将Vs0按式(11)换算为滩段流速U,然后取合理测点进行U-J之间的关系拟合(图5)得到,EC=1.269 m,λ=1.43(L=52.32 m),即:

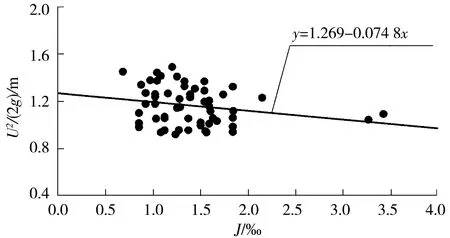
图5 修正通用阻力公式法U-J关系拟合

(22)

因为船舶上滩航行过程处于非匀速非直线运动状态,航行姿态多变,舵角和漂角常不稳定,推力与阻力常不平衡,惯性力难以计算准确,所以测点有一定散乱。但流速、坡降指标遵循消滩指标的内在关系,结果仍然符合总体统计规律。

3.4 坡流消滩指标

选用上述同样的测点,也可应用兹万科夫阻力公式法和通用阻力公式法进行转换,转换结果见图6和图7,同样可以给出坡流指标的关系式如下:

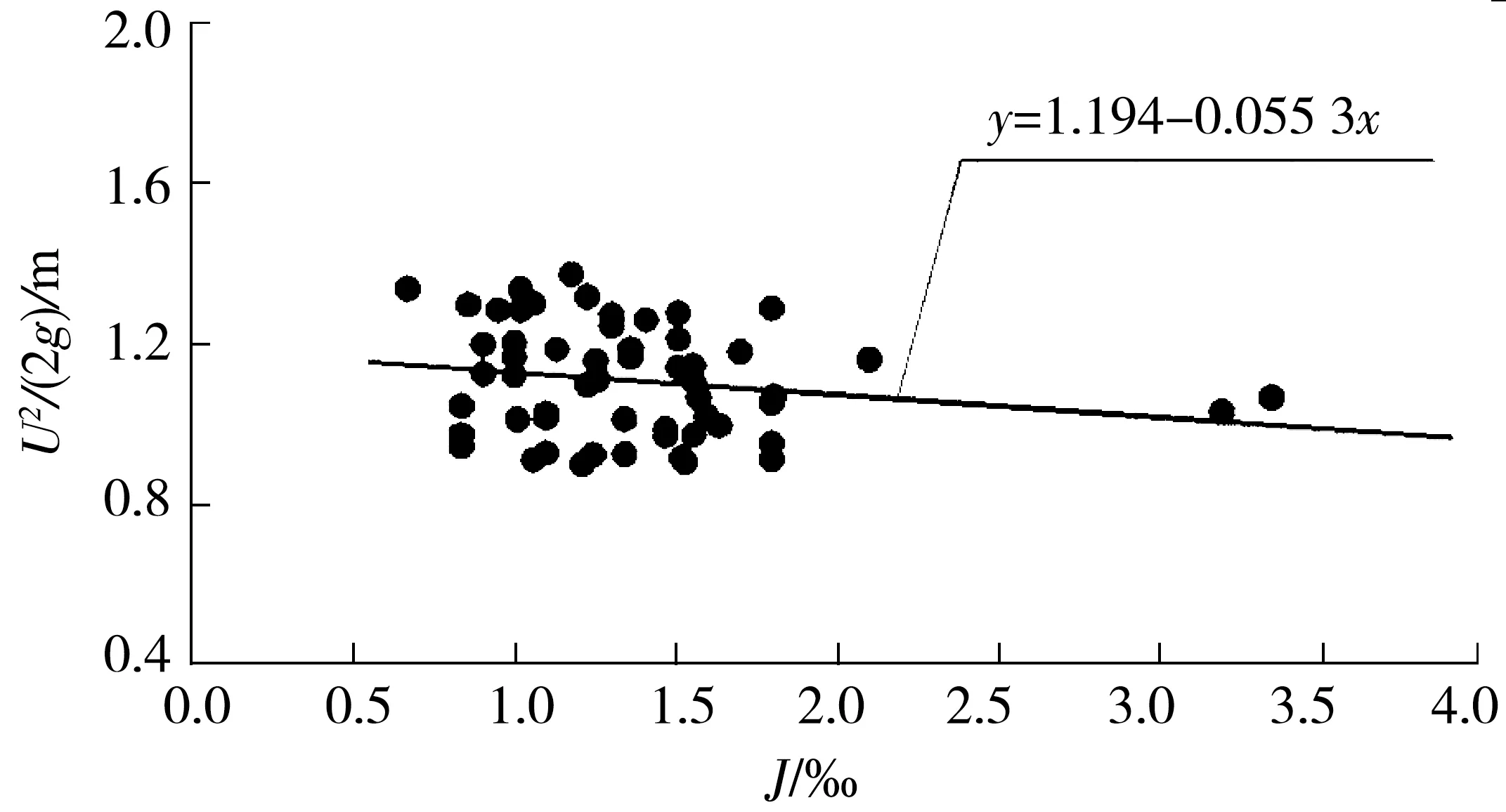
图6 兹万科夫阻力公式法U-J关系拟合

兹万科夫阻力公式法:

(23)

通用阻力公式法:

(24)

取比降J=0、1‰、2‰、3‰、4‰、5‰等分别代入式(22)～式(24),便可得到对应的流速指标U,计算结果见表4。从图8的对比可见,兹万科夫阻力公式法与修正通用阻力公式法较为接近,通用阻力公式法小比降时较大,大比降时较小,曲线随比降的变化较陡。

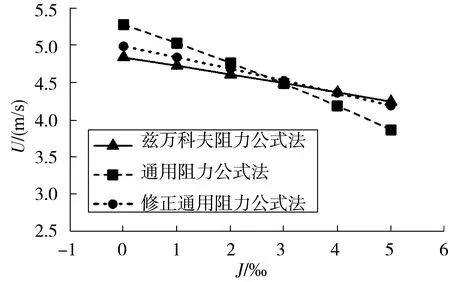
图8 消滩指标转换方法的比较

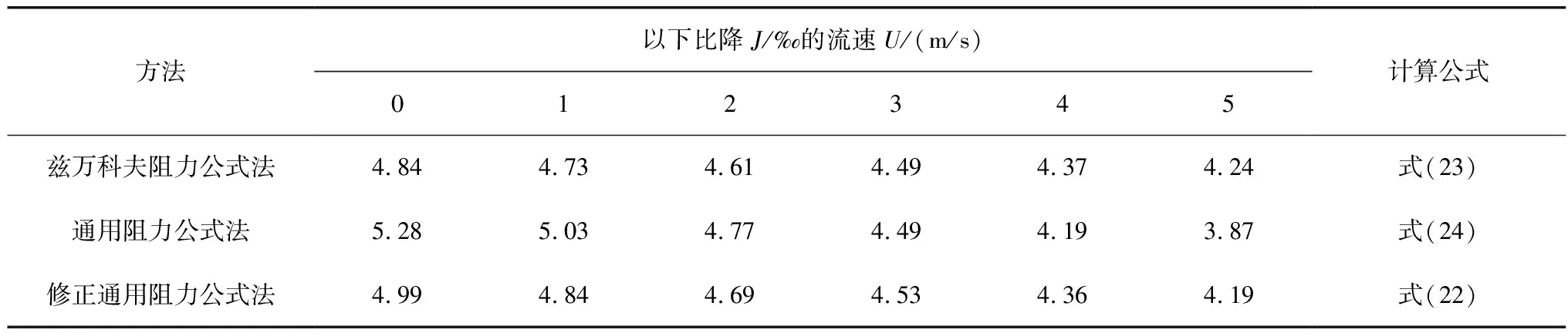
表4 试验船消滩指标

将J=0时对应的流速指标,由式(11)可反算回对水航速Vs0,可理解为额定工况的静水航速,故称之为似静水航速。兹万科夫阻力公式法J=0的U=4.84 m/s,反算Vs0=5.87 m/s,比静水航速6.15 m/s小4.6%,基本合理;通用阻力公式法J=0的U=5.28 m/s,反算Vs0=6.37 m/s,大于静水航速6.15 m/s,是不符合实际的;修正通用阻力公式法J=0的U=4.99 m/s,反算Vs0=6.04 m/s,稍小于静水航速6.15 m/s,说明是合理的。因此,修正通用阻力公式法应用了实船试验成果对水流阻力公式的修正,与兹万科夫阻力公式法相比,避开了繁琐的水流阻力计算,计算结果也基本一致,转换方法简便实用,为较好的非额定工况实船试验消滩指标的转换方法。

4 结 语

应用实船上滩试验确定消滩指标,比较理想的额定工况需满足额定载重、额定主机功率和航速刚好等于船舶上滩要求的最小航速等3个条件,对于仅额定载重和功率条件时,流速指标可采用对水航速等效的方法确定。

实船上滩航行一般难以保持匀速直线运动,受力平衡分析宜考虑船舶加速度引起的惯性力。通过非额定工况和额定工况各自遵循的受力平衡方程,可导出将非额定工况的实测对水航速变换为消滩水力指标对应航速的转换公式。其中关键在于水流阻力的计算方法,应用兹万科夫阻力、通用阻力及其修正的阻力公式,导出了3种消滩指标的转换方法。

依据澜沧江四级航道静水航速和上滩实船试验成果,通过测点数据的合理取舍、推进系数的计算、坡流指标的拟合等过程,得到了3个转换方法的消滩指标结果。通过对比发现,兹万科夫阻力法和修正通用阻力公式法计算结果较为一致,通用阻力公式法偏差稍大。鉴于修正通用阻力公式法应用了实船试验成果对水流阻力公式的修正,避开了繁琐的水流阻力计算,简便实用,为较好的非额定工况实船试验消滩指标的转换方法。