平行板电容器中介质受力问题的讨论
2023-10-07陈德智李卓凡
陈德智 李卓凡
(华中科技大学 电气与电子工程学院, 武汉 430074)
许多电磁场教科书在介绍虚功原理计算静电力时采用了这样一道例题[1-6]:如图1所示,介电常数不同的两块介质插入平行板电容器之间,求介质块所受的静电力。求解过程摘要如下:

图1 插入平行板电容器的两块介质块
忽略边缘效应,电场只存在于V1、V2区域,故E1=E2=U/d,电场能量为
(1)
式中,ε1、ε2分别为两块介质的介电常数;V1=bdl,V2=bd(a-l),分别是进入电容器内部的两块介质的体积,其中U是极板电压,d为极板间距,a为电容器长度,l为介质1进入电容器的长度,b为电容器垂直于纸面方向的深度。设介质1发生虚位移dl,采用虚功原理,得到介质受力[6]:
(2)
方向指向电容器内部,如图1所示。
另外有一些教材经常采用静电力导致液面升高的例子作为习题或例题(如文献[7-8]),原理与此相仿。
题目本身并无多大讨论价值,但是作为一道例题,涉及到电磁场教学中对电磁力作用机理与计算方法的正确理解。此题求解过程及结果的有趣之处在于,在忽略边缘效应的情况下,电场只有垂直分量,但是介质块却受到了一个横向的电场力。根据电磁场理论,材料所受的电磁力归根结底是材料中的电荷与电流所受的电磁力,即洛伦兹力:
F=q(E+v×B)
(3)
那么,垂直方向的电场如何产生了横向的作用力?
这个问题很早就被注意到,但几十年来,围绕这个问题的讨论一直络绎不绝,至今仍然有一些问题不够清晰,故有必要加以讨论和明确。
虚功原理是依据能量守恒原理,通过电场力虚拟做功引起的电场能量变化来计算物体的受力,它本身不涉及受力的机制。那么静电力是如何作用的?
1 关于介质受力机制的解释
1.1 边缘场是介质受力的根本原因
既然产生横向作用力必须依赖横向电场,而横向电场只存在于电容器极板的边缘之外,所以我们把目光移向介质露出在电容器之外的部分V1b和V2b,从边缘效应出发去寻找受力的解释。
如图2所示,考虑边缘电场,在介质露出电容器外的部分,电场具有横向分量且不均匀。介质极化产生的电荷效应,有两种表达方式:一种方式是考虑介质表面的极化电荷σp,所受电场力为

(a)极化电荷受力模型

(b)电偶极矩受力模型图2 极化介质的受力机制
f=σpE
(4)
如图2(a)所示,极化电荷σp会受到电容器极板向右的吸引力。
另一种方式是考虑介质内部的电偶极矩(单位体积的电偶极矩用极化矢量P表示),如图2(b)所示,在不均匀电场中,电偶极矩将受到向电场增大方向的作用力,也指向电容器方向[9-11]。
两种方法对于力的分布有所不同,但是计算介质的整体受力是等价的。以下采用电偶极矩分析,单位体积受到的静电力为:
f=(P·▽)E
(5)
对左侧介质进行体积分,得到整体所受静电力为

(6)
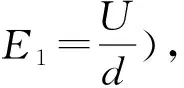
(7)
式中S=bd是介质块右端面面积。F1是左侧介质的受力,对应于式(2)中右侧介质为空气的情况。
从式(7)看,似乎是在介质右端面上受到一个单位面积为
(8)
的电场力。但是回顾式(7)的推导过程,就知道并不存在这样的力。式(6)清楚地表明,闭合面积分是只是数学变换的结果,并不表示力存在于端面上。
实际上,从式(6)的第三个等号
(9)
可以看到,介质位于电容器内部的部分,由于电场近乎均匀,▽E2近乎为0,对积分贡献可以忽略不计。对式(9)的贡献主要源自介质左侧露出电容器外部的区域,该区域电场不均匀,▽E2数值较大。
上述结果表明:介质块受到的力确实是来自边缘电场对露在电容器外的介质极化电荷的作用力。换言之:虽然虚功原理中没有计算边缘效应,但是边缘效应才是受力的根本,介质必须有一部分露出在电容器外部。
为进一步验证上述结论,采用有限元法和虚功原理计算了介质块从外部逐渐进入电容器过程的受力变化,如图3所示。结果表明,介质块进入电容器之前(l< 0 m)受到很小的力;当介质块右边缘即将接触电容器时(l=0 m),受力有一个极大值;随后,随着介质块部分进入电容器(0 m

(a)介质块从外部进入电容的计算模型
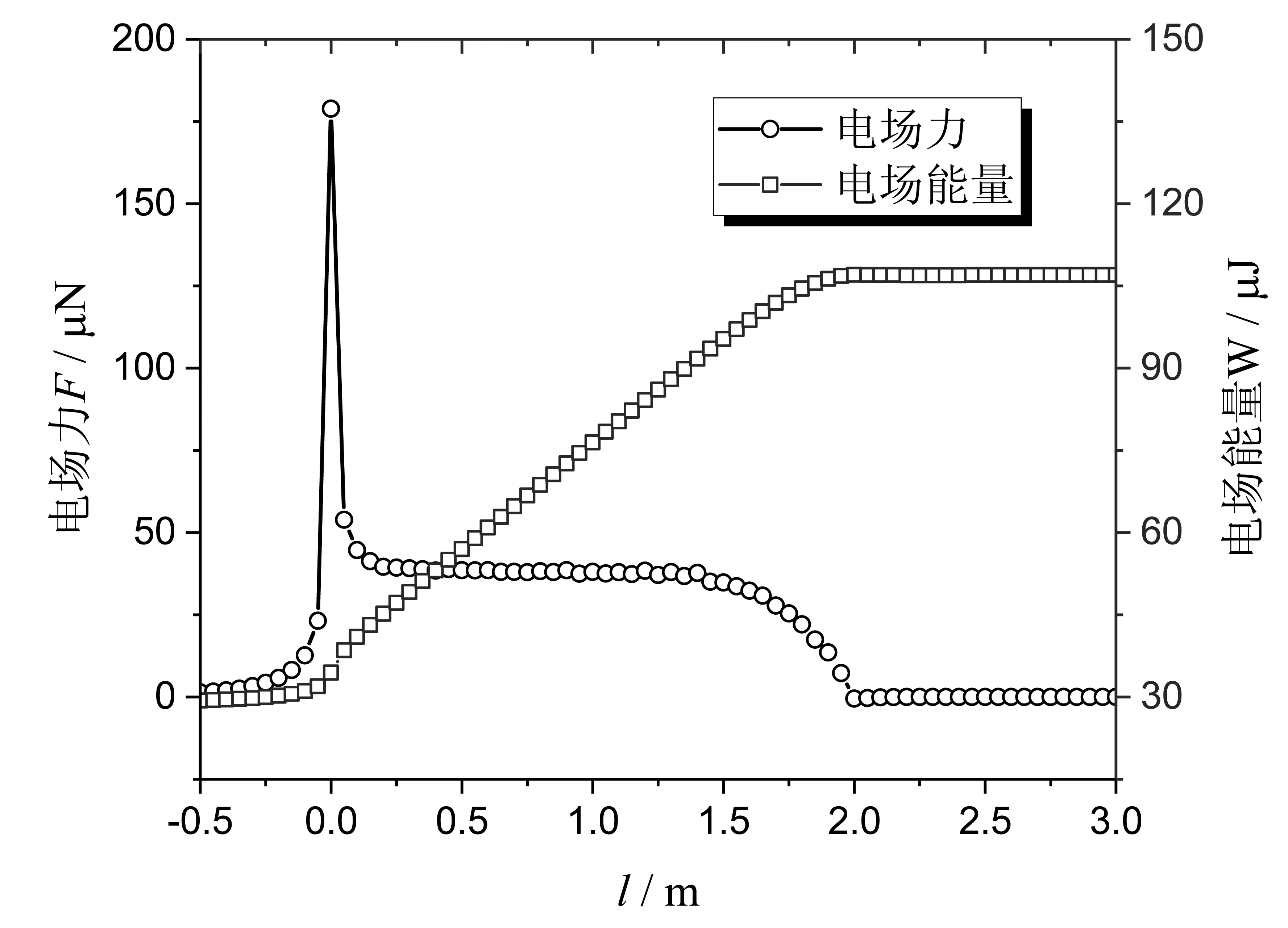
(b)介质块受力及系统能量随位置的变化

(c)根据有限元结果绘制的介质表面受力分布图3 介质块从外部进入电容器过程中的受力变化
进一步,根据有限元计算结果,绘出了介质表面极化电荷面密度受力分布f=σpE,如图3(c)所示。其积分结果与前文的结果吻合。该图直观地显示了介质受力分布。
计算模型参数:极板宽度a=5 m,极板厚度0.1 m,板间距d=1 m,极板深度b=1 m,板间电压为1000 V;介质块宽度为2 m,高度为1 m。l为介质块右边缘至极板边缘的距离,l<0 m表示介质块完全在电容器外部,l>0 m表示介质块已进入电容器;l=2 m表示介质块刚好全部进入电容器。电场力的计算采用虚功原理。参数是随意写的,只作数值验证用。
1.2 为什么忽略边缘效应可以得到正确的结果
既然边缘效应才是产生力的原因,为什么采用虚功原理时忽略边缘效应却可以得到正确的结果?关于这个问题,后续有学者做出了正确的解释[12]。简述如下:
回顾图1,设介质1和介质2都有部分进入了电容器,只要介质露在电容器外部的体积(V1b,V2b)足够大,当介质在电容器内发生微小的虚位移时,边缘区以及外部区域的能量是不变的,变化的只是电容器内部(V1+V2)的能量,因此对总能量求导也就是对这部分能量的求导。在这种情况下,只要电容器长度、宽度远大于极板间距,内部的电场就能够用E=U/d计算。只要满足这几个条件,忽略边缘效应就不会影响结果的正确性。
1.3 虚位移法得到的力是谁的受力
存在两种介质的情况下,虚位移法得到的力是谁的受力?这个问题通常容易被视而不见,多数时候会被笼统地问:“计算介质受力”,或者“交界面受力”(交界面下文将谈及)。但如果要深究,这个问题就必须予以明确。
发生虚位移时,两块介质一进一退都在运动;计算中求得的是包括两种媒质的系统的总能量变化,因此得到的是介质1与介质2的合力。
在1.1节中,根据电偶极矩得到了左侧介质1所受的电场力式(7),该计算过程与右侧介质2的存在与否无关。因此可以同样导出介质2的受力:
(10)
式中参考方向是从右侧进入电容器,故为-ex。
将式(7)与式(10)相加,得到两块介质受的合力为

(11)
与式(2)一致,说明式(2)确实是两种介质的合力。
1.4 关于交界面受力的讨论
“交界面受力”的说法被很多经典教科书采用,例如文献[3]。这个说法可能跟“法拉第力管”的概念有关。文献[3]是这样表述的:如图4所示,平行于电场线的交界面两侧受到压力,单位面积压力大小为:f1=ε1E2/2,f2=ε2E2/2,合力为
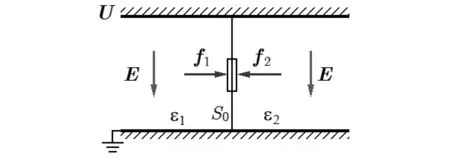
图4 交界面的受力:平行于E线的交界面受到压力
(12)
合力fa参考方向与f2一致。
应用式(12)于图1所示的交界面,得到界面受力为
(13)
的确与式(2)相同。
但是“交界面的受力”这个术语非常含糊。交界面是个几何概念,不是一个物理实体,如何理解一个几何概念受的力?在这个与E线平行的界面上,不存在极化电荷,那又如何理解它的受力?因此这种说法非常令人困惑。
在1.1节的讨论中已经阐明:采用闭合边界的面积分计算受力是数学变换的结果,不代表力存在与表面上。介质表面是否受力,要看表面上是否存在电荷的面密度(包括自由电荷面密度和极化电荷面密度),电荷面密度的受力由所在位置的电场强度决定,如洛伦兹力公式所描述。
1.5 对介质受力的一种错误解释
有一种解释,认为介质受的力来源于介质位于电容器内部的表面极化电荷受到右侧极板上自由电荷的引力[13])。如图5(a)所示,该模型假定极板外不存在电场,极板间电场均匀,在此条件下可以得到:介质表面的极化电荷密度为σp=-(ε1-ε0)U/d,极板与介质相接触部分的自由电荷密度为σ1=ε1U/d,位于介质右侧的部分自由电荷密度为σ2=ε0U/d。然后计算σ2在介质区域产生的电场,认为该电场对σp的作用力就是介质受到的力。在介质进入电容器深度l远大于极板间距d以及电容器长度a远大于l的情况下,得到的结果与式(7)相同。
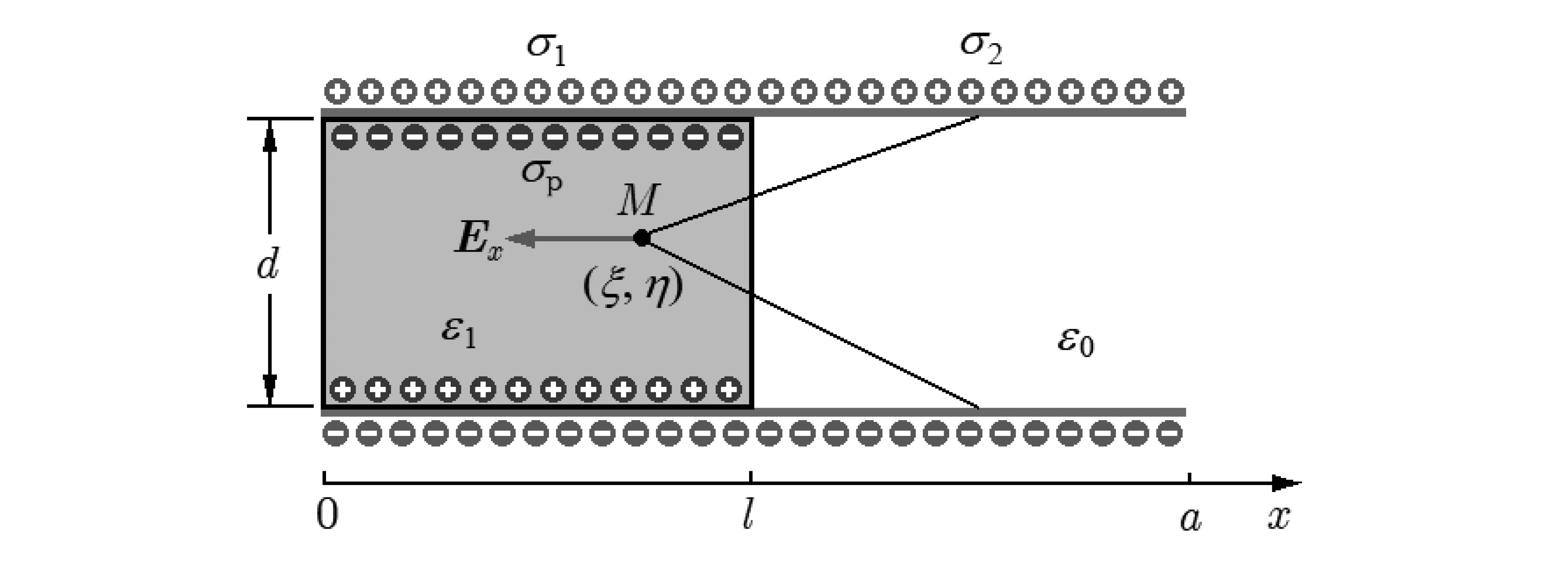
(a)一种错误的解释:极板右侧的自由电荷在介质中产生横向电场

(b)左右对称的结构才能保持介质中电场和电荷都是均匀的图5 极板表面的自由电荷与介质表面的极化电荷
文献[14]、[15]对该方法的模型和推导提出了质疑,但文献[12]又做了辩驳,否认有问题。直到新近,这种方法还被重复提起[16]。
先不论推导是否正确,这种方法明显与1.1节电偶极矩法不相容。在电偶极矩方法中,左侧介质进入电容器的部分对受力几乎没有贡献,而该方法则认为受力全部来自这部分的极化电荷。两种观点明显相互矛盾。很惊奇为什么同一篇文献会两种方法都认可。
仔细分析,该方法的模型设定是前后矛盾的。在预定模型中,忽略边缘效应,即假定了介质和空气中都只有垂直方向的均匀电场;但在计算过程中又得到了介质区域存在横向电场。第二个矛盾在于,在图5(a)所示模型中,极板电位为恒定值与假定电荷均匀分布是不可兼得的。只有如图5(b)所示的对称结构才可以同时保持极板电位恒定与电荷均匀分布,但此种情况下左右两侧的 在介质产生的横向电场分量又相互抵消了。不过,图5(b)可以帮助理解为什么这种不正确的方法能够得到正确的结果。
2 电容器内两块介质的受力分析
为进一步理解电场中介质的受力图像,考虑如图6所示完全位于电容器内部的两块介质。

(a)两块“悬空”的介质

(b)两块与极板相接的介质

(c)计算模型,电容器参数同图3;保持c=d/2图6 完全位于电容器内部的两块介质
首先做定性分析。图6(a)中,两块介质悬浮在半空,不与极板相接连。在电场作用下,介质表面出现极化电荷。按照同性相斥的原理,两块介质应该是相互排斥的。如果介质之间有间隙,则排斥力随间隙的增大而迅速减小。而在图6(b)中,两块介质上下表面与极板紧密接触,根据前面的分析,这种情况下电场只有垂直方向的分量,因此介质之间应该没有横向力的作用。
现采用有限元法对图6(c)所示的模型进行定量计算,改变介质间距及介质高度,观察介质受力变化,以检验上文的定性分析。计算分两部分。
2.1 “悬空”介质块之间的作用力。
保持介质块宽度和高度c=h=d/2不变,改变介质块之间的间距g,得到介质块受力大小如图7(a)所示,方向向左。由于介质块之间的相互作用力符合作用力与反作用力定律,因此只给出了介质块1的受力。结果表明:两块悬浮的介质块,在相互邻近时,彼此之间出现排斥力,且斥力随间距增大而迅速衰减,与定性分析一致。

(a)间距对悬空介质块作用力的影响(高度h=0.5 m)

(b)介质块高度对作用力的影响(间距g=0.05 m;h=1 m对应介质块与极板完全接触)

(c)根据有限元结果绘制的介质ε1表面受力分布图7 位于电容器内部的两块介质的作用力
2.2 介质块与极板间距对作用力的影响
保持介质块宽度c=d/2和介质块之间的间距g=0.05 m不变,改变介质块高度h,得到介质块受力大小如图7(b)所示,方向向左。结果显示,随着介质块高度增大,相互之间的排斥也随之增大。这是因为介质中的电场随介质块高度增大而增大,极化电荷面密度也随之增大,因此排斥力加强。但是当介质块高度接近极板间距d(计算中取值1 m)时,介质块之间的作用力迅速减小。这是因为此时电场的横向分量迅速减弱。当h=d,介质块与极板相接触,电场横向分量消失,介质块之间的排斥力也随之消失。所有变化规律都符合前面的预判。这个例子可以用来说明:介质的交界面并不必然产生电场力。
图7(c)根据有限元结果,绘制了介质ε1表面极化电荷面密度受力的分布。可以预见,如果没有ε2,介质ε1左右两侧的受力是对称的,因此合力为0(介质会受到一个向外膨胀的应力;但我们此处假定它是刚体,不考虑其变形)。从图中可以看到,由于介质ε2的存在,ε1右侧受力受到削弱,而左侧受力基本不受影响,因此整体受到向左的力,即ε1与ε2之间相互排斥。
3 结语
对介质块在平行板电容器内的受力这一经典例题进行了分析,围绕着作用力的产生机制,回顾了前人学者的一些工作,对一些方法和观点进行了剖析和讨论。核心观点可以概括为两点:
(1)介质中的电荷与电流(含自由电荷与极化电荷、自由电流与磁化电流及极化电流)所受的洛伦兹力是介质受力的唯一机制;
(2)要将电磁力的计算方法与受力机制区分开来。计算方法可以采用各种间接方法、等效方法,只需要结果正确,不必然反映受力的物理过程。
这些讨论有助于教学中对电磁作用力和相关计算方法的理解。观点不当之处欢迎批评讨论。
科学的发展是一个不断继承和创新的历程。强调创新肯定是正确的,但继承的重要性也不宜被削弱。科学发展到今天,人类知识的积累已极大丰富,知识的继承变得越来越艰难。明显的例证:人们求学的时间几乎占据了有效生命长度的1/4以上。继承与创新是相互相成的,不可偏废。忽视知识继承的艰巨性,不重视对过去知识的学习,所谓的创新,常常成为伪创新和假创新。数十年、上百年以前被发现过的现象不断被重新发现;几十年以前讨论过、指出过的错误仍然盛行,这样的例子不胜枚举。切磋和交流能帮助我们相互借鉴,要努力营造一种鼓励讨论和争鸣的氛围。
