分布式SCS-CN有效降雨修正模型建立及应用

申红彬，徐宗学，曹 兵，王海周

(1. 华北水利水电大学河南省水圈与流域水安全重点实验室，河南 郑州 450045；2. 北京师范大学城市水循环与海绵城市技术北京市重点实验室，北京 100875；3. 东营市水务局，山东 东营 257091)

随着城市化的快速发展，特别是低影响开发(Low Impact Development，LID)和海绵城市建设的稳步推进，地表下垫面种类日趋多样，LID设施作用日渐突出，降雨径流规律更为复杂。如何对变化环境下城市的降雨径流过程进行模拟，是当今水文学，特别是城市水文学研究的重点与难点[1]。SCS-CN(Soil Conservation Service Curve Number)模型是美国农业部水土保持局于1954年开发研制的一款降雨径流模型[2]，因结构简单、输入参数较少、对观测数据要求不高，在城市降雨径流模拟、流域水土保持等多个方面得到了广泛的应用，且特别适用于资料相对缺乏的地区。不过，在SCS-CN模型的应用与发展过程中，如何对其进行改进与完善始终是研究的热点与难点问题。

SCS-CN模型形式较多，其标准模型的建立主要基于水量平衡方程以及2个基本假设：地表径流量与可能最大径流量的比例和累计入渗量与当时可能最大滞留量的比例相等；初损值与当时可能最大滞留量成比例关系。模型参数主要有当时可能最大滞留量(或曲线数)和初损系数，方程结构相对简单。对于SCS-CN标准模型的改进主要包括：① 模型参数的率定与修正。如考虑前期降雨、坡度等对当时可能最大滞留量(或曲线数)的影响，分析初损系数的变化范围与区域特征等[3-4]。② 模型的分布式改进与应用。如以栅格为基本单元，建立分布式的SCS-CN模型，并探讨模型参数的尺度效应[5-6]。③ 模型假设条件与内部结构的改进。如将累计入渗量分解为静态与动态下渗量，并引入前期土壤水分改进累计入渗量与当时可能最大滞留量的比例关系等[7-10]。其中，对SCS-CN模型的分布式改进与应用是重要的发展方向，更适用于下垫面组成与产流规律复杂的流域。模型假设与内部结构的改进有助于进一步增强模型的理论基础，有效提高模型的精度，但往往会使模型参数增加，方程结构形式更趋复杂。因此，在SCS-CN标准模型简单方程结构的基础上，如何通过引入修正系数即可实现模型改进，并建立相应的分布式模型，成为一个有待研究的问题。

本文基于SCS-CN标准模型，经与SCS-CN改进模型比较，引入有效降雨修正系数，提出建立SCS-CN有效降雨修正模型；对于城市LID复杂区域，构建基于水文响应单元的分布式SCS-CN有效降雨修正模型，以北京双紫园小区为例对其降雨径流过程进行模拟应用。

1 模型建立

1.1 SCS-CN标准模型及其改进模型简介

SCS-CN标准模型以水量平衡方程为基础：

P=Ia+F+R

(1)

并结合2个基本假设：

(2)

Ia=λS

(3)

联合式(1)—式(3)推导，可以得到地表径流深的计算公式如下：

(4)

式中：P为降水量，mm；Ia为初损量，mm；F为累计下渗量，不包括Ia，mm；R为地表径流深，mm；λ为初损系数，主要取决于地理与气候因子，取值范围为0.1～0.3，一般取均值为0.2；S为当时可能最大滞留量，是累计下渗量的上限，mm。

在λ=0.2条件下，由式(4)可知当时可能最大滞留量与降水量、径流深具有如下关系：

(5)

式(5)是利用降雨径流资料对当时可能最大滞留量的反推，最终取算术平均值。在实际计算中，由于当时可能最大滞留量数值变化范围很大，为便于取值，引入量纲一参数径流曲线数(CN)，两者转换关系为

(6)

式中：NC为CN值，受到土壤类型、前期湿度、植被状况、坡度以及土地利用等因素影响，理论取值范围为0～100，实际变化范围为40～98。

现有对于CN值取值的主要步骤包括[11]：① 根据土壤下渗或产流能力，进行水文组分类(分为A、B、C、D 4类)；② 结合土地利用类型、植被覆盖与水文状况(分为好、中、差3类)等，查SCS手册选取CN值；③ 考虑土壤前期湿润程度(AMC)影响，引入前期降水指数(API，至少前5 d累计降水量)，分级(分为AMC Ⅰ级/干旱、AMC Ⅱ级/正常和AMC Ⅲ级/湿润)换算与取值；④ 考虑坡度影响，对CN值进行坡度修正。不过，由于CN值变化规律复杂，往往还需调整优化。

SCS-CN改进模型是在标准模型式(1)的基础上，进一步将累计下渗量分解为静态下渗量与动态下渗量[2，7-10]，如图1所示，并将假设条件式(2)改写为：

(7)

Fc=fct

(8)

经过联合推导，可以得到地表径流深的计算公式如下：

(9)

式中：Fc为静态下渗量，mm；Fd为动态下渗量，mm；fc为静态下渗速率，mm/min；t为产流后降雨历时，min。

1.2 SCS-CN有效降雨修正模型的建立

比较SCS-CN标准模型式(4)与改进模型式(9)，后者因引入静态下渗量参数而变得复杂。不过，从本质上来看，式(4)中的(P-Ia)与式(9)中的(P-Ia-Fc)均可视为有效降雨，后者数值明显小于前者。因此，通过引入有效降雨修正系数，可以将两者统一表示如下：

(10)

式中：κ=(P-λS-Fc)/(P-λS)，为有效降雨修正系数。

式(10)即为SCS-CN有效降雨修正模型。其中，当κ=1.0时，式(10)为SCS-CN标准模型式(4)；当κ<1.0时，式(10)等效于SCS-CN改进模型式(9)。基于SCS-CN有效降雨修正模型式(10)，经过推导，可以得到径流系数的变化方程：

(11)

式中：α为径流系数。

根据式(11)，当P→∞时，P/(P-λS)→1、α→κ。因此，κ表征了径流系数随降水量增大而变化趋向稳定的极限值。实测资料表明[12]，对于渗透地表，其径流系数随降水量增大而变化趋向稳定的极限值一般小于1.0。

(12)

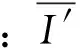
对于均匀降雨过程，当降雨强度与下渗速率相等时，地表开始产流。以产流时刻为初始时刻，结合Horton土壤下渗模型，有：

f=(f0-fc)exp(-βt)+fc

(13)

(14)

I=f0

(15)

式中：f为下渗速率，mm/min；f0为产流开始时下渗速率，mm/min；β为变化速率，1/min；I为均匀降雨强度，mm/min。

考虑到产流时刻I=f0，相应有：

(16)

将式(16)代入式(12)，可以得到均匀降雨条件下κ的计算表达式为

(17)

从式(17)可以看出，在均匀降雨条件下，κ主要与下垫面土壤的下渗特性参数有关。

1.3 分布式SCS-CN有效降雨修正模型的构建

对于由多种下垫面组成的复杂流域，为反映降雨、下垫面等条件空间分布不均的影响，建立分布式模型是重要的发展方向。以往多采用对不同类型下垫面CN值按面积比例进行加权平均的方法(式(18))[13]，并应用于SCS-CN模型，但最终效果仍为集总式模型，难以深入描述流域不同类型下垫面的产流贡献与变化规律。

(18)

式中：NC，a为流域综合CN值；NC,j为不同种类下垫面CN值，m2；A为汇流区域总面积，m2；Aj为不同种类下垫面面积，m2；j为不同种类下垫面编号；m为下垫面种类数量。

现有流域离散化的方法主要有单元网格、山坡单元、自然子流域、水文响应单元、等流时面积单元、典型单元面积、分组响应单元及其组合等[14]。比较来看，水文响应单元是在自然子流域划分的基础上，进一步结合土地利用方式、植被类型和土壤类型，划分为下垫面特征相对单一和均匀的离散响应单元，更为符合SCS-CN模型CN取值的分类思路。

对于城市LID复杂区域，可以按下垫面种类、LID设施及其组合划分为不同类型的水文响应单元(如需汇流计算还要考虑空间位置进一步细分)，构建分布式SCS-CN有效降雨修正模型。其中，需要说明如下：① 分别对不透水地表、渗透地表及LID设施进行水文响应单元划分及编号。② 对于不透水地表，累计下渗量F=0，降雨径流损失主要为地表填洼损失，更宜采用Linsley公式进行模拟；对于渗透地表及LID设施，可以构建基于SCS-CN有效降雨修正模型的分布式模型。③ 对于有些LID设施，需考虑其蓄存容积对降雨径流的影响[15]。例如对下凹绿地等，在计算底部土壤下渗产流后，还需考虑上部下凹容积对产流的蓄存作用，下凹容积蓄满外溢后的水流方为下凹绿地降雨径流。④ 对于有些不透水地表，也需考虑中端蓄水池、蓄水罐等蓄水设施对地表径流的蓄存作用。具体方程如下：

(19)

(20)

R=R′+R″

(21)

2 应用案例

2.1 研究区概况

北京双紫园小区是北京市最早开展雨水利用的示范工程之一。该小区位于海淀区双紫支渠南侧、北洼路西侧，由3栋塔楼、1栋排楼以及一些配套建筑物组成(图2(a))，总面积约2.3 hm2，其中建筑屋顶面积约0.6 hm2，道路、庭院、停车场面积约10 hm2，绿地面积约0.7 hm2(表1)[16]，土壤类型为重壤土，稳定下渗率为0.3 mm/min。小区汇流区域分为屋顶(包括2栋塔楼，汇流面积约1 350 m2)与道路(包括不透水/透水路面、绿地、庭院、停车场等，汇流面积约15 088 m2)。2004年9月，基于LID理念，小区对地表下垫面进行了升级改造。具体改造措施包括：① 增铺透水铺装，相应面积由880 m2增至4 582 m2；② 绿地下凹改造，将小区内绿地下挖5 cm，对于一些下挖难度较大的绿地，则用石埂圈围，使其达到下凹绿地的效果。

表1 小区土地利用类型及面积百分比统计表Table 1 Statistics of land use types and area percentage

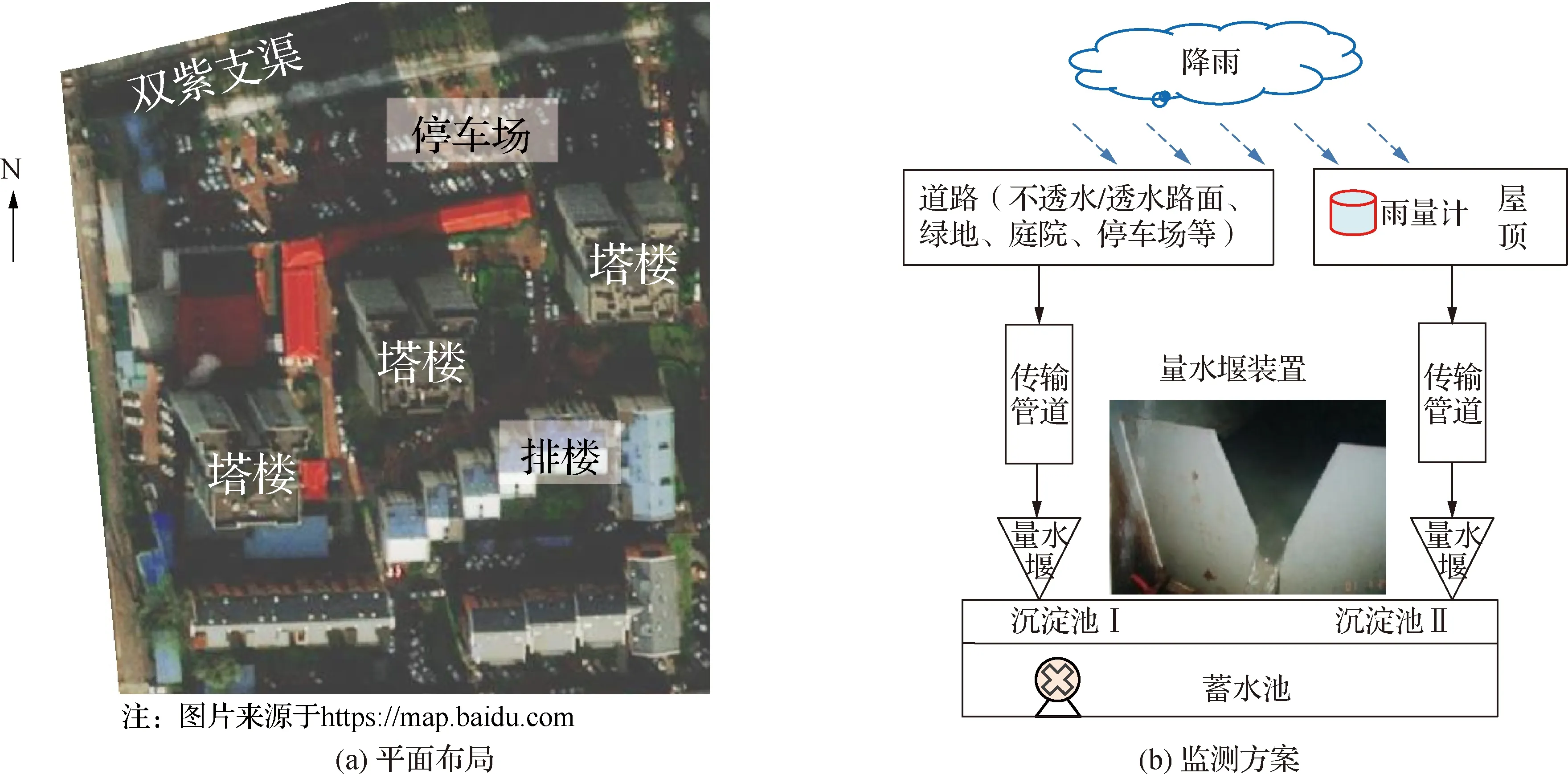
图2 小区平面布置与降雨径流监测方案示意Fig.2 Plane layout and rainfall-runoff monitoring scheme in the study area

2.2 降雨径流监测数据

北京双紫园小区在地表下垫面改造前后均开展有降雨径流实际监测。其中，降雨监测采用自记式雨量计进行连续监测，仪器安装在住宅楼顶部，相关数据直接记录在存储卡上，记录间隔时间为1 min，每隔一定时间人工去现场通过数据线连接电脑读取；径流监测采用“液位计+三角堰”测量方法，分别在屋顶与道路管道末端安装三角堰(图2(b))并配置液位计，对水位及流量过程进行连续监测，液位计数据自动存储在系统内，记录间隔时间为1 min，每隔一定时间人工去现场通过数据线连接电脑读取。基于液位计量测水位过程数据，通过堰前水位与流量关系曲线换算为流量过程；对不同场次降雨流量过程，通过时间积分，可以得到场次降雨径流量，径流量与汇流面积相除可以转化为径流深。

图3为收集、整理得到的双紫园小区地表下垫面改造前后道路汇流区域的降雨、径流监测数据，共计有51场有效降雨、径流数据。其中，地表下垫面改造前为18场，降水量为8～51 mm，径流深为0～14 mm；改造后为33场，降水量为5～88 mm，径流深为0～12 mm，径流削减效果明显。另外，图中还给出根据前5 d累计降水量对不同场次降雨土壤前期湿润程度的判别结果。可以看出，除个别情况外，多数情况下土壤前期湿润等级为AMC Ⅰ级。

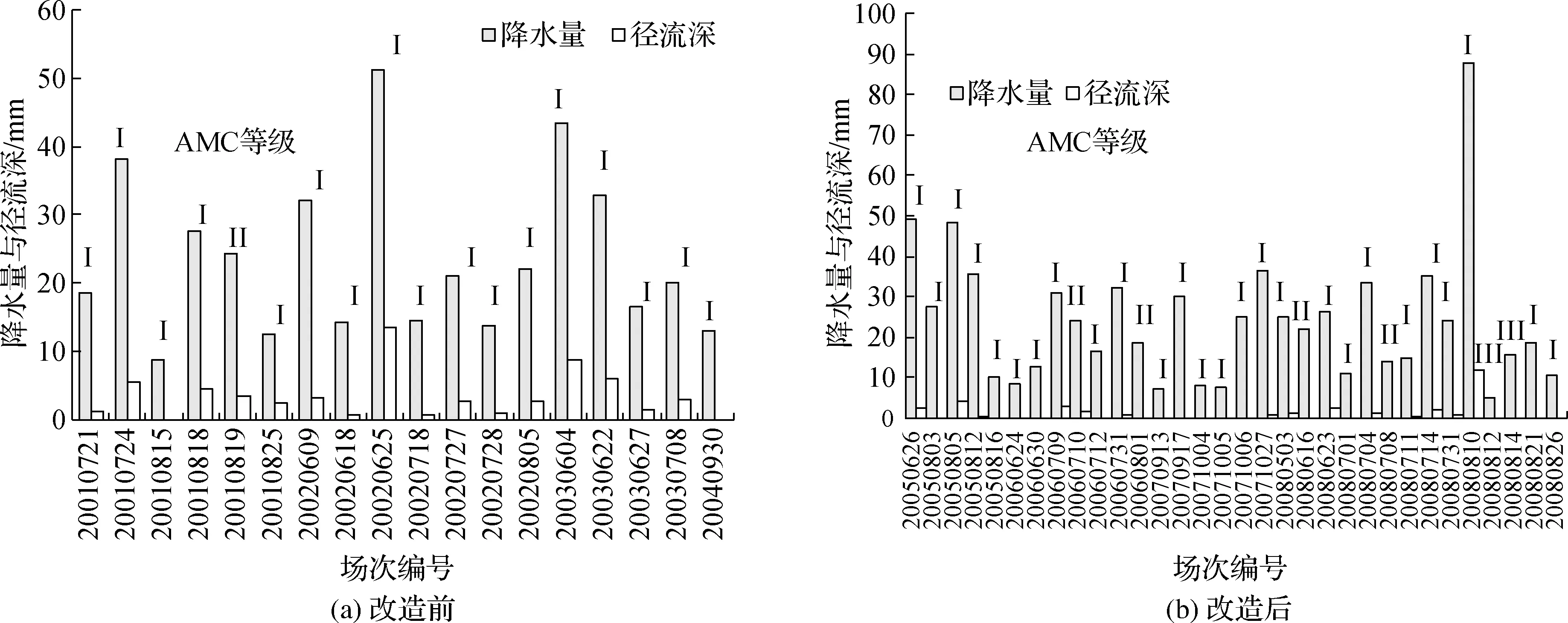
图3 道路汇流区域降雨、径流监测数据Fig.3 Rainfall and runoff monitoring data of the road watershed

3 模型应用结果

3.1 模型效果评价指标

分别采用确定性系数(R2)与Nash-Sutcliffe效率系数(ENS)对模型效果进行量化评价[17-18]。其中，确定性系数是评价模拟效果最为基本的评价指标，变化范围为0～1.0；Nash-Sutcliffe效率系数是判定残差与实测值数据方差相对量的标准化统计值，变化范围为-∞～1.0；两者数值越趋近于1.0说明模型精度越高，当ENS≤0时说明模拟值与实测值存在较大偏差。相应计算公式分别为：

(22)

(23)

式中：Ro，i为径流深实测值，mm；Rc，i为径流深计算值，mm；i为序号；n为样本容量。

3.2 模拟结果与讨论

基于分布式SCS-CN有效降雨修正模型，并对渗透地表分别取κ=1.0与κ<1.0(具体率定)，对双紫园小区不同场次降雨径流进行模拟，包括参数率定、模型应用与验证：

(1) 参数率定。以小区地表下垫面改造前道路汇流区域的降雨、径流监测数据为基础，开展模型参数率定，结果如表2所示。其中，对于曲线数CN值的率定，首先，根据式(5)反推计算当时可能最大滞留量，并取算术平均值约为50.5 mm，相应CN值约为83；其次，通过查阅SCS手册，并根据土壤前期湿润等级，初步选定绿地、透水铺装等下垫面CN值；最后，对不同类型下垫面CN值进行优化调整，并要求不同类型下垫面CN值按面积加权平均值在83左右。另外，不透水道路最大填洼损失值(Δmax)较大，是由于其相连地下管网末端安装有三角堰，形成一定的蓄水空间，这里进行了综合考虑。

表2 模型参数与效果评价统计表Table 2 Statistics of model parameters and performance evaluation results

(2) 模型应用与验证。基于表2中的模型参数，结合小区地表下垫面改造后道路汇流区域的降雨、径流监测数据，开展分布式SCS-CN有效降雨修正模型的应用与验证，结果如图4所示，相应确定性系数与Nash-Sutcliffe效率系数值同列于表2。

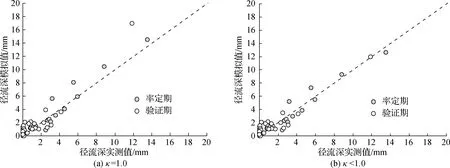
图4 分布式SCS-CN有效降雨修正模型径流模拟值与实测值比较Fig.4 Comparison between the simulated and measured runoff using the distributed SCS-CN model with revised effective precipitation

综合图4与表2可以看出，基于分布式SCS-CN有效降雨修正模型，并对渗透地表有效降雨修正系数分别取值等于1.0与小于1.0，两者对双紫园小区不同场次降雨径流深的模拟值与实测值散点均位于45°线附近、符合较好，确定性系数与Nash-Sutcliffe效率系数分别为0.91与0.83、0.92与0.91，后者效果优于前者，说明对渗透地表有效降雨修正系数取值小于1.0能够有效提高模拟效果。后期，应在前述有效降雨修正系数计算表达式(12)、(17)的基础上，进一步深入分析不同降雨与下垫面土壤下渗条件对κ值变化的影响。

4 结 论

本文基于SCS-CN标准模型，经与SCS-CN改进模型比较，通过引入有效降雨修正系数，构建SCS-CN有效降雨修正模型及其分布式模型，并开展模型应用与效果检验，得到主要结论如下：

(1) 对于SCS-CN有效降雨修正模型，当对修正系数取值等于1.0时，其等同于标准模型，当对修正系数取值小于1.0时，其等效于改进模型；修正系数表征了径流系数随降雨量增大而变化趋向稳定的极限值。

(2) 对于城市低影响开发复杂区域，综合考虑低影响开发设施蓄存容积对降雨径流的影响，构建了基于水文响应单元的分布式SCS-CN有效降雨修正模型。

(3) 应用分布式SCS-CN有效降雨修正模型，分别对渗透地表有效降雨修正系数取值等于1.0与小于1.0，两者对不同场次降雨径流深的模拟值与实测值散点均位于45°线附近、符合较好，确定性系数与Nash-Sutcliffe效率系数值分别为0.91与0.83、0.92与0.91，后者效果优于前者，说明对渗透地表有效降雨修正系数取值小于1.0能够有效提高模拟效果。