微电网恒输出功率“光伏+储能”系统的功率和储能容量研究
2023-10-07杨海涛
杨海涛
(中国电建集团水利水电第十一工程局有限公司,郑州450001)
0 引言
储能技术常被用于电网调峰、峰谷套利、区域调频等场景。目前,储能技术包括蓄电池储能、飞轮储能、压缩空气储能、抽水蓄能等类型,其对提高供电可靠性,改善电能质量有明显作用[1]。光伏发电在新能源领域占有重要地位,使用光伏发电有助于碳中和[2]目标的实现。但光伏发电受天气的影响较大,具有波动性、间歇性、输出功率无法恒定的特点,其并入电网会对电网负荷造成冲击,且其也无法直接接受电网的调度,导致负荷和电网供求不平衡的情况出现。针对上述情况,电网会要求光伏电站与储能系统相结合,以保持整个电站的输出功率恒定,达到稳定电网的目的。
光伏发电系统与储能系统组成的“光伏+储能”系统作为一个微电网,针对其配置问题,既要考虑光伏发电的波动性特点,又要考虑光伏发电系统总体光伏发电量与储能容量的关系。储能容量和负荷容量共同决定着光伏发电系统的装机规模,而合理的计算储能容量是保证“光伏+储能”系统经济、稳定运行的必要条件。刘俊峰等[3]提出微电网的主动能量管理理念,以博弈理论研究了可调负荷和储能的互动,论述了电站运营的优化方案。刘畅等[4]综述了储能装置在微电网领域的容量规划、运行策略及优化目标,主要阐述了不同储能方式对微电网中规模、成本、响应速度等要求响应不同的侧重点。吴小刚等[5]提出了一种以负荷电率和能量溢出比为目标的独立光伏储能容量优化方法。贾禾等[6]研究了动态电价对储能容量选择的影响。倪驰昊等[7]提出以储能电池电量、功率,光伏发电消纳能力为约束条件的采用分时电价的“光伏+储能”系统优化策略。殷仁豪等[8]针对运行中的风电场和光伏厂区进行逐时数据分析,并基于经济性最优对储能容量配置进行研究。文献[5-8]中分析优化储能容量主要是为了充分利用光伏电力,但对于可满足电网恒功率供电要求的储能容量的配置方式而言,适用性不强。为了解决此问题,本文在电网有充电限制的条件下,根据“光伏+储能”系统需在每天固定时间段内恒定输出功率的要求,提出一种通过综合考虑“光伏+储能”系统平准化度电成本(LCOE)和净现值收益率来分步确定此类系统最大恒输出功率及储能容量的方法,并以某项目为例,利用MATLAB软件进行模拟仿真验证。
1 “光伏+储能”系统的结构
“光伏+储能”系统的结构示意图如图1所示。
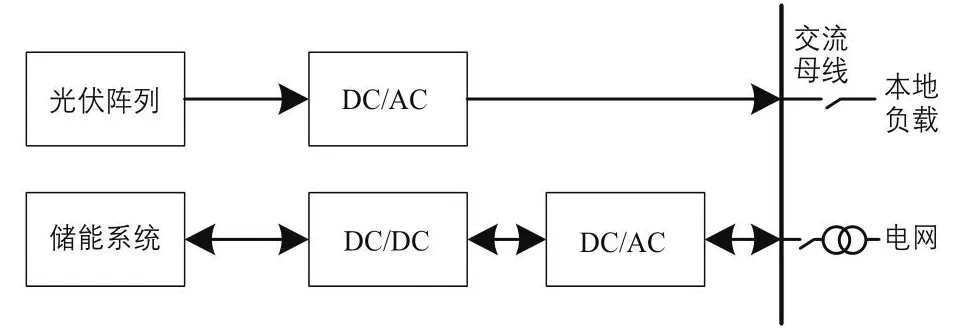
图1 “光伏+储能”系统的结构示意图Fig.1 Structural diagram of “PV+ energy storage” system
在光伏发电满足负载需求且有多余电能时,可将电力输入电网,或为储能系统充能;当光伏发电不能满足负载需求时,由储能系统单独供电或与电网共同对负载供电。储能系统可由光伏发电系统或电网侧进行充电。
典型的“光伏+储能”系统恒输出功率曲线如图2所示。图中:h1~h4为业主要求的“光伏+储能”系统开始恒功率输出的时间,其中,h1~h2和h3~h4段分别为输出功率线性上升阶段和线性下降阶段;p1、p2均为输出功率。
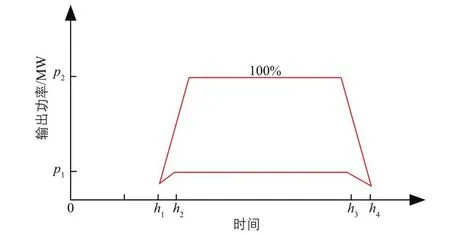
图2 典型的“光伏+储能”系统恒输出功率曲线Fig.2 Typical constant output power curve of“PV+ energy storage”system
通过图2可发现:h2~h3时间段内“光伏+储能”系统输出功率需在p1~p2之间对电网保持恒定输出,在此时间段内不允许电网向储能系统充电,且电网的反向充电时间和充电功率均受到限制。
本文将以先确定光伏发电量,然后确定系统最大输出功率,最后确定储能容量的顺序进行分析。
2 光伏发电量计算
光伏发电系统主要由光伏组件、光伏支架、逆变器、开关柜和变压器等设备组成,其输出功率主要受光伏组件自身性能和光照资源的影响。在进行光伏电站设计时需考虑多种因素,比如:当地的光照资源、地质条件、可用区域范围、装机规模、发电量、光伏支架类型、逆变器类型、并网方式等。当光伏电站设计完成后,即可求得该光伏电站全生命周期内的各年发电量。光伏发电量计算流程图如图3所示。
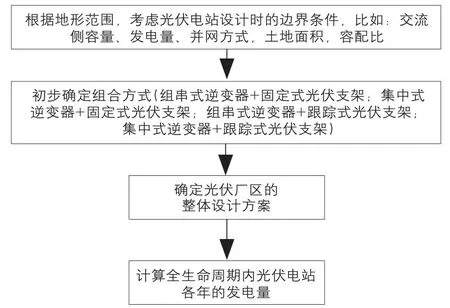
图3 光伏发电量计算流程图Fig.3 Flow chart of PV generating capacity calculation
3 “光伏+储能”系统最大恒输出功率的计算
“光伏+储能”系统最大恒输出功率的计算流程为:1)确定同一时间段不同的恒输出功率值;2)计算不同恒输出功率下的净现值收益率,并根据最大净现值收益率来确定“光伏+储能”系统的最大恒输出功率。
根据光伏发电系统典型年的光伏发电量找出其最大输出功率和最小输出功率,并结合对“光伏+储能”系统要求的输出功率的限制,综合考虑“光伏+储能”系统的功率输出范围,建立每种输出功率下的弃光量和发电量的关系,利用净现值收益率作为判断条件选出“光伏+储能”系统最佳输出功率。
在无电网给储能电池充电的情况下,“光伏+储能”系统的弃光功率和发电量的关系为:1)在储能容量足够的情况下,当“光伏+储能”系统以最大恒输出功率向电网供电且光伏发电量完全被电网消纳时,光伏发电系统多余的输出功率可由储能系统全部存储,整个“光伏+储能”系统不弃光;2)在储能容量被限制的情况下,当光伏发电系统的发电量在某段时间内大于储能容量和电网消纳能力之和时,“光伏+储能”系统会存在弃光现象。上述两种情况分别由式(1)和式(2)计算。
式中:pds为弃光功率;Qday为光伏发电系统的日发电量;h为“光伏+储能”系统需要供电的时长;ps为“光伏+储能”系统向电网供电时的最大恒输出功率。
“光伏+储能”系统的日弃光量Qds可表示为:
式中:hsr为纯光伏发电满足恒输出功率的发电时长;pdi为储能系统的放电功率。
“光伏+储能”系统的年发电收益A可表示为:
式中:i为一年中的第i天;C为售电电价。
“光伏+储能”系统的净现值收益率RNPV可表示为:
式中:IN为“光伏+储能”系统的初始投资;PF为“光伏+储能”系统不满足供电要求时的罚款金额,PCF为“光伏+储能”系统的充放电价差额;y为“光伏+储能”系统的全生命周期,本文取20年;r为“光伏+储能”系统的投资回报率。
综合考虑年发电收益、初始投资、罚款电量等因素,以式(5)作为判别条件得到“光伏+储能”系统的最大恒输出功率。
4 储能系统中储能电池容量的计算
储能系统由储能电池电芯、功率变换器(PCS)、系统组件和辅助部分(比如:空调、消防装备、照明设施、不间断电源(UPS)、计量装置等)、电池管理系统(BMS)、能量管理系统(EMS)等组成。
目前储能系统中的储能电池普遍采用磷酸铁锂电池。储能系统与光伏发电系统的结合方式可采用直流耦合和交流耦合两种方式,当应用于高容配比场景时,多采用直流耦合方式,夜间深度调峰;当应用于新能源发电系统、源网、配套储能系统和多能互补系统等场景时,多采用交流耦合方式。
储能系统的放电倍率由PCS和储能电池电芯共同决定。储能电池的容量受老化损失、系统效率、电池效率、实际放电倍率、放电时间、放电功率等因素影响;储能电池的容量会随着循环次数和使用时间的增大而减小。由于光伏发电系统输出功率受到天气影响会出现较大波动,因此储能系统的PCS功率要尽量接近“光伏+储能”系统的输出功率,保证储能系统在短时间内充满电量,使储能系统、光伏发电系统和电网能满足供电要求。
储能系统充放电约束满足以下公式:
式中:pdis为储能系统额定放电功率;Soc(t-1)为(t-1)时刻储能系统的电量;Soc,min为储能系统最小储电量;ηdi为放电效率;t为时刻;Δt为(t-1)时刻与t时刻的差值。
式(6)表示了储能系统的放电约束条件,储能系统的放电功率为储能系统额定放电功率和匹配储能系统剩余容量放电功率中较小的一个。
式中:pch为储能系统的充电功率;pchm为储能系统额定充电功率;ηch为充电效率;Soc,max为储能系统最大储电量。
式(7)表示了储能系统的充电约束条件,储能系统的充电功率为储能系统额定充电功率和匹配储能系统剩余容量充电功率中较小的一个。
式中:pch(t)为储能系统t时刻的充电功率;pdi(t)为储能系统t时刻的放电功率。
式(8)表示储能系统t时刻存储的电量由初始电量和到达t时刻后最终储存的电量组成,并且需保证储能系统最小的存储电量,防止储能电池过放电影响其寿命。
储能系统储能容量的范围界定首先是根据典型年每天的太阳辐照度逐时数据计算光伏发电系统首年及之后各年的发电量,同时综合考虑首年和末年的发电量最大值、最小值,以及电网要求的储能系统最大输出功率、最小输出功率和储能系统衰减因素来确定储能容量的最大和最小范围;然后根据此范围,以“光伏+储能”系统LCOE最低、净现值收益率最高为目标求解。
求解过程中,首先计算各种储能容量下不由电网反充电时,每天通过光伏发电向储能系统可以充电的最大容量和“光伏+储能”系统上网不足电量;然后根据电网反向给储能系统充电的功率和时间限制,计算出储能系统由电网所充的电量。
储能容量的计算步骤为:1)根据“光伏+储能”系统最大输出功率和供电时间,由电网购电限制等因素确定储能容量的范围;2)计算不同恒定功率条件下净现值收益率,并确定“光伏+储能”系统最大恒输出功率;3)确定“光伏+储能”系统中储能系统的储能容量。
平准化度电成本CLoe的计算式可表示为:
式中:Ce为设备使用残值;CM为设备维护费用;Q(y)为第y年的发电量。
5 算例分析
“光伏+储能”系统恒输出功率曲线与光伏发电曲线如图4所示。
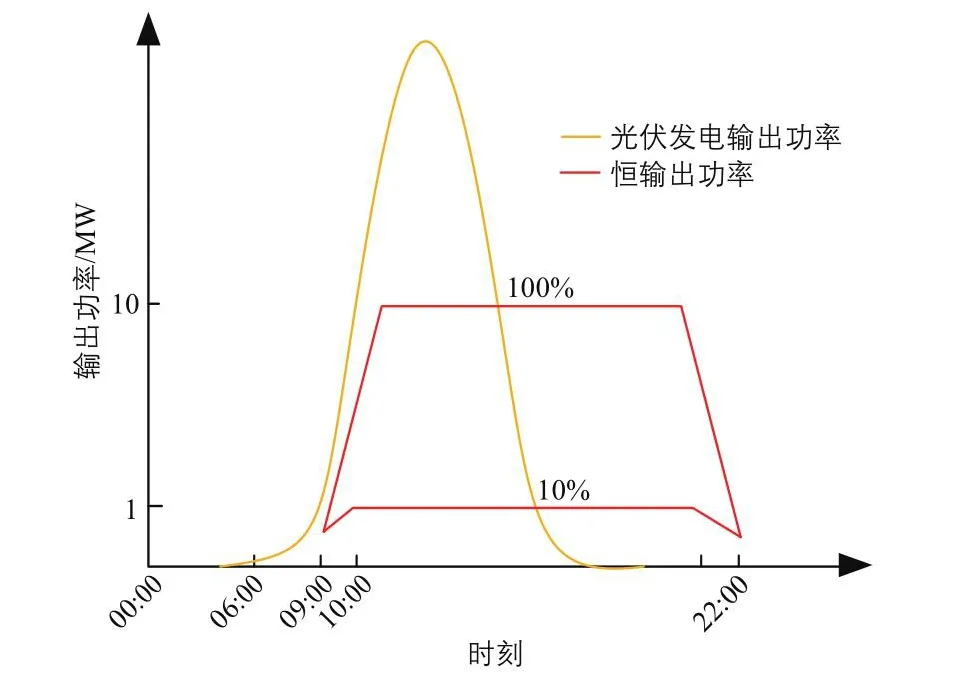
图4 “光伏+储能”系统恒输出功率曲线与光伏发电输出功率曲线Fig.4 Constant output power curve of“PV+energy storage”system and PV power generation output power curve
由图4可知:“光伏+储能”系统需要在10:00~21:00保持恒输出功率,恒输出功率误差在±10%内,且最低输出功率不能低于电网报备功率的10%(电网报备功率即“光伏+储能”系统最大恒输出功率),即最低输出功率不小于1 MW,而且在此时间段内不允许由电网充电;09:00~10:00为线性上升阶段、21:00~22:00为线性下降阶段。可充电时间为00:00~05:00,允许以最大输出功率2 MW对储能电池充电。
“光伏+储能”系统需保证20年稳定供电同时保持最大输出功率。
若光伏发电系统和储能系统的总占地面积约为0.25 km2,则需提前预测1天的发电量并按照此预测值根据向电网报备的功率输出曲线对电网进行供电。
5.1 光伏发电系统配置
根据选定的土地面积,设计光伏发电系统直流侧装机容量为24 MW,共44718块540 W的单面单晶硅光伏组件;交流侧采用7台3125 kW的集中式逆变器,峰值功率为23.7 MW;采用固定式光伏支架,光伏支架排布间距为7 m;在此布置方式下计算无限制条件时20年内光伏发电系统的各年发电量。计算结果如表1所示。
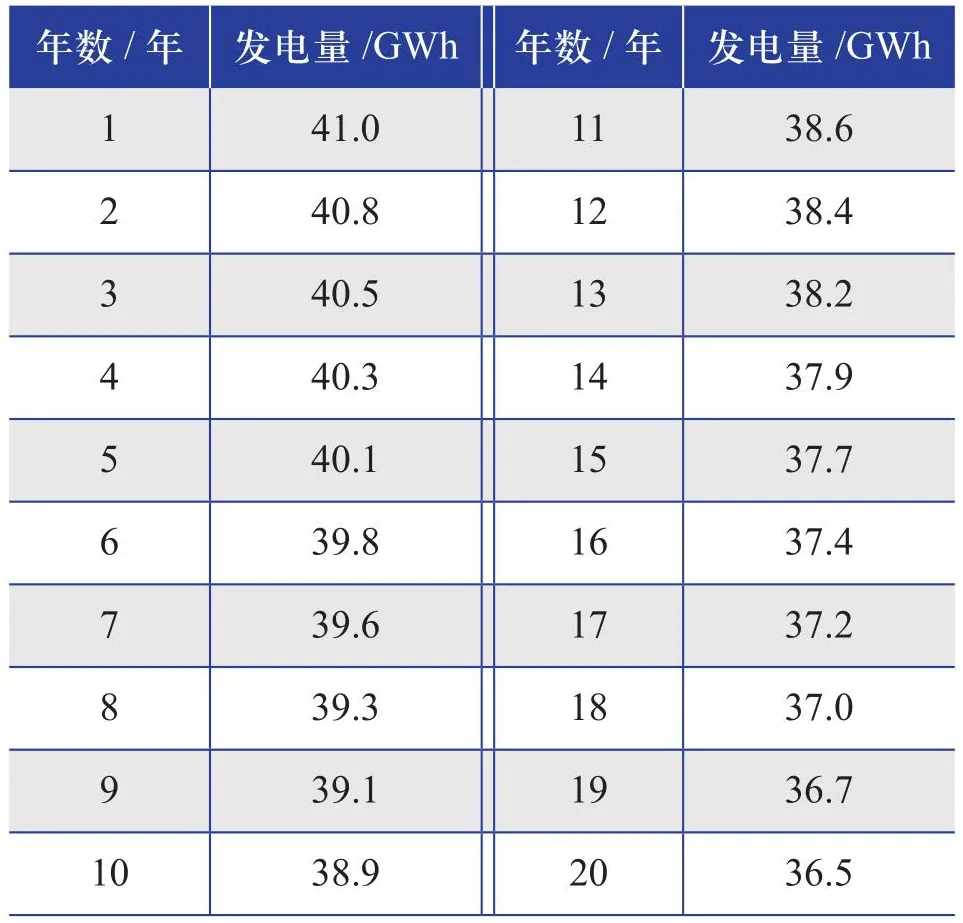
表1 20年内光伏发电系统的各年发电量Table 1 Annual power generation of PV power generation systems within twenty years
5.2 “光伏+储能”系统向电网报备的最大输出功率选择
根据上文中“光伏+储能”系统最大恒输出功率的计算步骤,本案例中恒输出功率供电时间等效为12 h;最低供电功率要求为1 MW,根据逐日光伏发电量计算得到首年单日最大发电量为161 MWh,等效恒输出功率为13.4 MW。因此,“光伏+储能”系统最大恒输出功率在1~13 MW之间进行选择。要求的储能供电时间段为从纯光伏发电输出功率达不到恒输出功率要求时起一直到要求的供电截止时间之间的时间段。
根据式(5)计算各最大恒输出功率下的“光伏+储能”系统的净现值收益率,计算结果如图5所示。
从图5可以看出:随着最大恒输出功率的值由1 MW增加到9 MW,“光伏+储能”系统的总发电量和总收益现值也随之增加;当“光伏+储能”系统最大恒输出功率为9 MW时,净现值收益率曲线达到最高点,此时为“光伏+储能”系统恒输出功率的最优解。
5.3 储能容量选择
储能系统参数设置为:储能电池充放电效率取79%;放电截止值取5%;考虑电池衰减,当电池可用容量低于65%时,淘汰电池。在满足项目最小输出功率的要求和合理的经济范围前提下,经初步计算,储能容量分别选取36、42、48、54、60 MWh;并且为保持“光伏+储能”系统需要的储能容量,根据储能电池衰减曲线考虑第7年和第15年增容,以达到第20年时储能容量仍能满足业主要求。光伏发电系统与储能系统采用交流耦合方案。需要说明的是,若未要求“光伏+储能”系统最终的容量则性能衰减则不需要考虑。
仿真软件的其他参数设置为:“光伏+储能”系统恒定最大输出功率定为9 MW;根据电网要求的10%最小输出功率且不小于1 MW,设定最小输出功率为1 MW;罚款电量为规定输出功率时间内小于10%的预测输出功率的部分。
成本与收益方面的设置为:储能系统单位造价取35万美元/MWh;光伏发电系统单位造价取750美元/kW;储能系统年运维成本为0.2美元/MWh;售电收入取0.25美元/kWh。
仿真步骤为:
1)首先根据光伏发电系统全年每天的输出功率,绘制输出功率曲线,作为预测值。其中,对于平均输出功率小于1 MW的情况,设置为1 MW,而对于平均输出功率大于9 MW的设定为9 MW。需要说明的是,本案例假设每天的预测光伏发电输出功率经过平均化后,整体的预测误差在10%内。
2)根据输出功率预测曲线先计算夜晚不充电时,在各种储能容量下储能系统每天通过光伏发电可以充得的最大容量和“光伏+储能”系统上网不足电量;然后根据电网反向向储能系统充电的功率和时间段,计算当天夜晚(22:00~24:00)储能系统可容纳的充电容量。
3)基于夜晚充电模式计算储能系统存储的电能,当光伏发电输出功率大于预测值时,多余的电力可为电池充电;当储能系统的荷电状态为100%时弃光;当光伏发电输出功率小于预测值时,光伏发电系统和储能系统共同工作;当储能系统达到放电截止值时,停止向电网供电。
仿真结果如图6~图8所示。
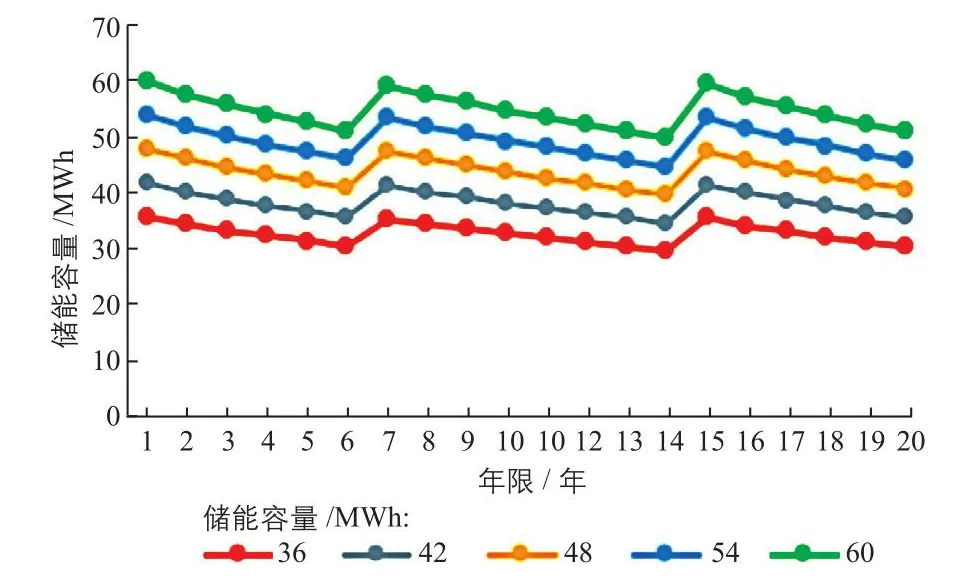
图6 20年内储能容量的变化趋势Fig.6 Trend in energy storage capacities over past twenty years
从图6单个储能容量20年内的变化趋势和图7单个储能容量下“光伏+储能”系统的发电量曲线可以看出,“光伏+储能”系统的总体发电量和储能容量呈正相关。当储能容量在36~48 MWh之间时,其对系统发电量提升较为明显;当储能容量在54~60 MWh之间时储能容量对“光伏+储能”系统发电量的提升帮助很小。这一规律可以从图8的弃光率曲线可以看出,随着储能容量的增加,弃光率曲线由较大斜率逐渐变得平缓。
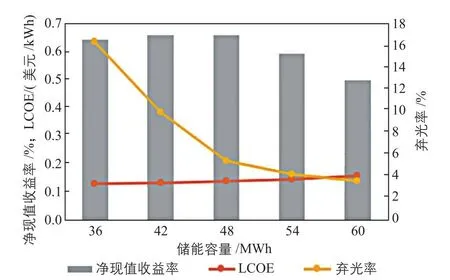
图8 不同储能容量下LCOE、净现值收益率和弃光率之间的关系Fig.8 Relationship between LCOE,net present value yield,and abandonment ratio under different energy storage capacities
从图8可以看出:虽然储能容量由36 MWh向60 MWh变化时弃光率逐渐减小,但由于储能成本增加,导致净现值收益率逐渐降低LCOE逐渐加大;储能容量为42 MWh时,净现值收益率最大,此时LCOE较低,为0.136美元/kWh,这说明优化储能容量有助于提高净现值收益率。综合考虑LCOE和净现值收益率后选择42 MWh为储能容量。
针对固定规模的光伏电站,其发电量固定在某个范围内,光伏发电量为边际效应产生的主要因素。储能容量的限制因素主要来自设备成本价格、弃电量、电价、罚款电量等,其容量能否合理选择是决定电站收益的决定性因素。
6 结论
本文在电网有充电限制的条件下,根据“光伏+储能”系统需在每天固定时间段内恒定输出功率的要求,提出了一种通过综合考虑“光伏+储能”系统LCOE和净现值收益率来分步确定此类系统最大恒输出功率及储能容量的方法,并以某项目为例,利用MATLAB软件进行了模拟仿真验证。仿真结果表明:本文所述计算方法有效解决了微电网恒输出功率要求下储能设备容量选择问题。
针对受天气影响的光伏发电的不确定性和输出功率预测误差对“光伏+储能”系统输出电量的影响需要进一步研究。未来随着储能电池价格降低,其衰减老化程度会随着新储能电池技术的发展而降低,储能系统将在新能源领域发挥不可或缺的作用。
