含摩擦作用叠梁应力势函数对煤层顶板的破坏研究

经来旺 ，方 旭 ，肖起辉 ，张世翔 ，焦建军 ，经 纬

（1.安徽理工大学 土木建筑学院，安徽 淮南 232001；2.大柳华能庆阳煤电有限责任公司 核桃峪煤矿，甘肃 庆阳 745000）

随着煤矿资源开采的由浅入深，巷道围岩所处地应力不断攀升，巷道顶板破坏几率大幅增加，使得煤矿企业的安全、经济、高效生产受到更大威胁。研究煤层顶板的破坏形式和机理能够有效地降低巷道支护成本；并为巷道顶板安全性能评估提供理论依据；因此对煤层顶板破坏的研究具有较高的工程价值。

由于煤层顶板破坏研究的重要价值，我国学者在该领域不断深耕并取得了丰硕的研究成果，这些成果主要可以分为3 类：即理论研究、相似实验以及仿真分析。在理论研究方面，王楠等[1]分析了急倾斜煤层端面顶板稳定性；左建平等[2-4]提出了覆岩“类双曲线”的破坏移动机理；孟浩[5]分析了不同采高下顶板垮落规律；冯国瑞等[6-8]提出了层间岩层的“块体梁-半拱”结构；王家臣等[9]提出了顶板岩块“破坏形态转变点”判别准则；杜华溢等[10]研究了非均匀应力对巷道围岩应力和变形破坏特征；张锋等[11]研究了采动前后巷道围岩塑性区分布与演化特征。在相似实验方面，贾栋等[12]利用相似模拟实验研究了综放工作面覆岩破坏特征；熊祖强等[13]采用模拟试验研究了复合顶板覆岩破坏及裂隙演化规律；池小楼等[14]开展了下分层开采再生顶板破断倾向分区演化及应力分布特征研究；张杰等[15]分析了煤层开采过程中覆岩运移破断特征及采动裂隙分布形态。在数值分析方面，刘治成等[16]利用FLAC3D软件分析了不同顶板开切眼围岩变形情况和塑性区发育特点；孔德中等[17]采用UDEC 软件对不同情况下煤壁变形情况进行模拟研究；赵毅鑫等[18]利用CDEM 软件对采场围岩应力和裂隙分布进行模拟。

上述成果均为煤层顶板破坏特征及机理的研究做出了重要贡献，并为后续的理论、试验以及模拟分析提供借鉴。然而地下巷道工程中，围岩岩性分布具有差异性，使得煤层顶板应力的分析存在误差。为此，将煤层直接顶与间接顶视为叠梁，引入弹性力学应力势函数，结合摩尔-库伦准则对模型强度进行分析，分析岩石参数对煤层顶板破坏的影响；以期为巷道煤层顶板的支护以及安全性能评估提供理论模型和依据。

1 模型建立

1.1 叠梁模型

在煤层开采过程中，其掘进工作面两侧会各留有一定厚度的煤柱，在工作面上部是由多种岩性不同的岩层组成，将其简化为直接顶与间接顶，工程示意图如图1。由于直接顶与间接顶的岩性不同，在此引入叠梁模型，将直接顶与间接顶简化为上部受均匀荷载的叠梁模型，其计算简图如图2。图2 中：h1为间接顶厚度；h2为直接顶厚度；l为叠梁跨度；q为上部岩层均匀载荷；μ为上下层之间的摩擦系数；b为叠梁厚度。

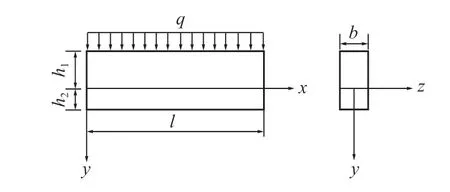
图2 模型计算简图Fig.2 Sketch of model calculation

1.2 应力势函数

为了分析叠梁剪应力与正应力及其分布特征，引入叠梁的应力势函数φi如式（1）：

式中：Ai1～Ai9为待定常数；i为层号，i=1 为上层，i=2 为下层。

待定常数取值表见表1。

表1 待定常数取值表Table 1 List of values of undetermined constants

由弹性力学中平面问题的平衡微分方程：

式中：σx为x方向应力；σy为y方向应力；τxy为剪应力；x、y为距离。

得到应力分量，可以用应力函数表示，如式（3）：

将式（1）代入式（3）中，得到上下层的应力分量：

式中： σix为x方向应力； σiy为y方向应力；τixy为剪应力。

2 顶板破坏分析

煤层开采过程中，顶板破坏的主要原因是由于顶部煤层内部存在大量且不规则分布的各类节理，并导致分析其强度会变得非常困难，但在结合大量的工程实践后表明，煤层顶板的破坏可以大致分为离层与断裂。在此将顶部煤层中分布的节理进行简化处理。简化节理模型如图3。

图3 简化节理模型Fig.3 Simplified joint model

以四川龙门峡南煤矿3131 工作面煤层开采实际情况，将煤层作为直接顶，将泥质灰岩作为间接顶，得到的力学参数见表2。

表2 煤层顶板参数Table 2 Parameters of coal seam roof

3 强度影响

针对简化后的模型，讨论直接顶与间接顶之间的摩擦力对节理的剪切强度与拉伸强度的影响，由摩擦力公式得到：

式中：f为摩擦力； σn为法向正应力。

将式（4）代入式（5）中，得到：

3.1 对剪切强度的影响

对水平节理进行强度分析，结合摩尔-库伦准则得到水平节理的强度计算公式：

将式（4）代入式（7）中，得到：

令Fτ为节理的剪切强度，得到：

若Fτ＞0，则节理未破坏，若Fτ≤0，则节理已破坏。将 μ=0.1 代入式（9）中，得到的Fτ与沿着x与y方向距离的曲面如图4；将Fτ＞0 的曲面投影到xy面，得到的Fτ未破坏区域的投影如图5。

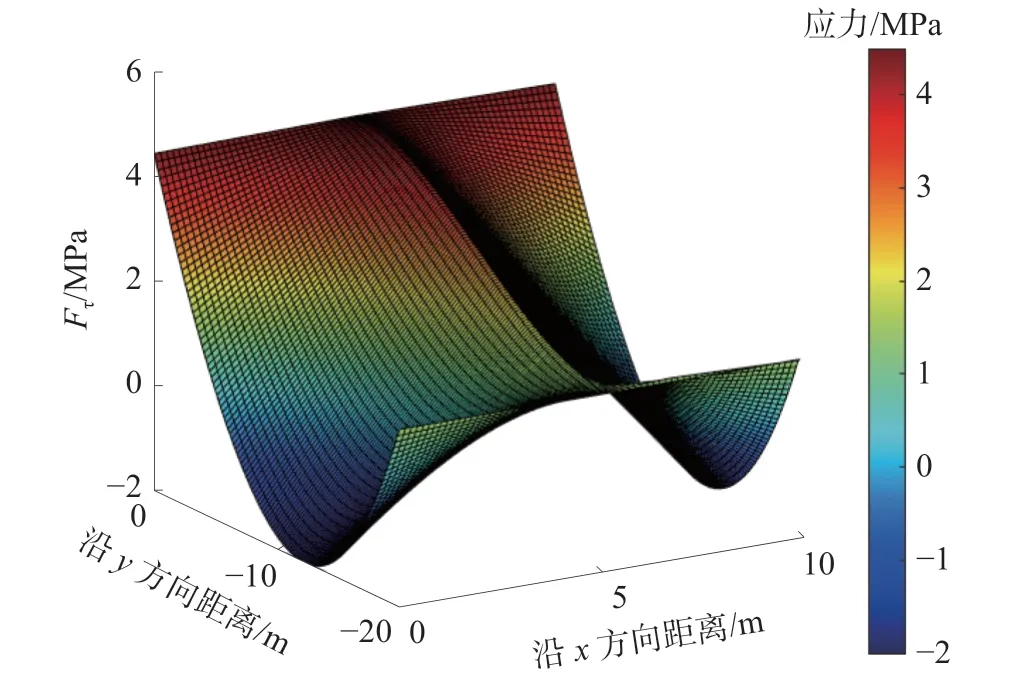
图4 Fτ曲面图Fig.4 Fτ-surface diagram

图5 Fτ投影图Fig.5 Fτ-projection drawing

从图4 可以发现，Fτ曲面图呈马鞍型；而从图5 可以看出，Fτ的破坏区域投影呈上陡下平的“类双曲线”左右对称分布。

3.2 对拉伸强度的影响

根据简化后的节理模型，对垂直节理进行强度分析，得到垂直节理的强度校验公式：

式中：FT为正应力差；T为抗拉强度； σix为水平正应力。

同样FT满足：若FT＞0，则节理未破坏，若FT≤0，则节理已破坏。将 μ=0.1 代入式（10）中，得到的与沿着x与y方向距离的曲面如图6；将FT＞0的曲面投影到xy面，得到的FT未破坏区域的投影如图7。

图6 FT曲面图Fig.6 FT-surface diagram

图7 FT投影图Fig.7 FT -projection drawing

从图6 可以发现，FT曲面图呈丝带型；从图7可以看出，FT破坏区域投影呈对称拱形分布。

综上所述，含摩擦作用叠梁应力势函数对煤层顶板破坏的规律可以总结为：①导致煤层顶板破坏的原因可简化为水平节节理与垂直节理，其中，水平节理是造成顶板离层的主要原因，垂直节理是造成顶板断裂的主要原因；②煤层顶板离层区域呈左右对称且上陡下平的“类双曲线”分布，煤层顶板断裂区域呈拱形分布。

4 岩层对顶板破坏的影响

由叠梁应力势函数中的待定常数A17可知，叠梁的应力分布与上下层之间的摩擦力和弹性模量及高度有关。而由式（6）可知，层间摩擦力是受摩擦系数和弹性模量及高度影响的，所以层间摩擦力和弹性模量及高度是对顶板破坏的主要影响因素。为了探究层间摩擦力对顶板破坏的影响，这里可以采用控制变量法来进行下一步研究。保持间接顶上部载荷和模型尺寸不变，通过分别改变摩擦系数大小和直接顶与间接顶的弹性模量比值与高度比值，从而得到离层破坏宽度以及断裂破坏高度与上下层摩擦系数大小和弹性模量以及高度比值的变化规律。

4.1 摩擦系数对顶板离层与断裂的影响

为了探究岩间摩擦系数对顶板离层与断裂的影响，保持直接顶与间接顶的弹性模量比值与高度比值不变，依次增大层间摩擦系数 μ，控制摩擦系数在0～0.2 之间，其他参数取值见表2。

4.1.1 摩擦系数对离层宽度及高度的影响

由式（9）可得：

联合表1 和表2，将各弹性模量下的待定常数代入式（11）中，得到Fτi关于x、y的函数。令Fτi=0，得到函数f(xi)，对f(xi)求偏导得：

令式（12）等于0，得到函数极值点中y值为：

将式（13）代入f(xi)中即可得到离层宽度。

将x=0代入式（11），得到函数的2 个解分别为y1、y2，2 个解的差值即为离层高度，即：

式中：hτ为离层高度。

4.1.2 摩擦系数对断裂高度的影响

由式（10）可得：

令FTi=0，得到一段拱形曲线的函数为f(yi)，由于f(yi)左右对称，故在x=l/2处取得最大值：

式中：ymax为断裂高度。

摩擦系数对顶板破坏影响如图8。

图8 摩擦系数对顶板破坏影响Fig.8 Effect of friction coefficient on roof damage

从图8 可以看出：随着摩擦系数的增大，离层破坏高度与宽度均有明显降低，这是由于摩擦系数越大，层间摩擦力也越大，岩层的抗剪强度也会随之增大；而断裂高度随着摩擦系数的增大也随之增大，但上升趋势并不明显，摩擦系数对断裂高度的影响比较小。

4.2 弹模比值对顶板离层与断裂的影响

为了探究2 种岩层弹性模量的比值对顶板离层与断裂的影响，同样采用控制变量法，在各岩层属性和直接顶与间接顶厚度及摩擦系数不变的情况下，保持直接顶的弹性模量不变，依次增大间接顶的弹性模量，改变直接顶与间接顶的弹模比值范围在1～5 之间。

首先计算出不同弹模下应力势函数的待定常数，将所得待定常数分别代入式（13）、式（14）和式（16）中，得到的弹模比值对顶板破坏影响如图9。

从图9 可以看出：随着间接顶弹性模量的增大，离层宽度与高度和断裂高度均有上升趋势，这是由于随着间接顶弹性模量的增大，其刚度也会随之变大，而应力则会向刚度大的地方转移，造成更大的破坏面积。

4.3 层高比值对顶板离层与断裂的影响

为了探究岩层高度的比值对顶板离层与断裂的影响，运用控制变量法，在其他条件不变情况下，保持直接顶与间接顶总厚度不变，改变直接顶与间接顶的高度比值范围在2～10 之间。

计算出不同高度比值下应力势函数的待定常数，将所得待定常数分别代入式（13）和式（16）中，得到的层高比值对顶板破坏影响如图10。

图10 层高比值对顶板破坏影响Fig.10 Effect of layer height ratio on damage of roof

从图10 可以看出：层高比值对顶板的破坏有显著的影响，当间接顶的层高增加时，离层宽度显著提升，这是由于层高在待定常数中的阶数高于弹性模量的阶数；对于断裂高度，随着间接顶层高的增加，断裂破坏高度有着明显降低，这是由于间接顶层高的增加，叠梁的中性轴上移，使得正应力在下部集中，从而导致破坏高度降低。

5 实例模拟验证

选用由周均民等[19]所做的动态相似模拟试验作为验证，顶板随工作面推进垮落图如图11。按照上文推导出的顶板破坏形态，煤层顶板的垮落区域应该是离层和断裂破坏区域的交集。

图11 顶板随工作面推进垮落图Fig.11 Roof caving with working face advancing

从图11 可以看出：随着工作面的持续推进，顶板也沿着推进方向以斜边垮落，其垮落模块大致可分为水平与垂直方向。沿着工作面的推进方向，其顶板交替出现破坏。模拟试验结果符合以上推导分析，从而进一步验证了含摩擦作用叠梁应力势函数对煤层顶板破坏分析的正确性。

6 结 语

1）煤层顶板的破坏可大致分为2 类：由水平节理造成的离层和由垂直节理造成的断裂。离层破坏区域呈上陡下平的类双曲线分布；断裂破坏区域呈对称的拱形分布。

2）当岩层岩性及高度不变时，层间摩擦系数越大，顶板破坏的就越小；当岩层层高及摩擦系数不变时，间接顶岩性越强，顶板破坏范围就越大；当岩层岩性及总高度不变时，间接顶越高，离层宽度也随之增加。

3）通过理论推导分析及模拟验证，可以说明简化叠梁模型能对煤层顶板破坏进行合理解释，为煤层顶板破坏区域的计算提供分析模型。