非确定工作状态下机械系统可靠性研究
2023-10-07李茹茹
李茹茹
(胜利油田龙玺石油工程服务有限责任公司,山东 东营 257000)
目前,社会大部分机械系统都具备复杂的内在结构和多样化功能。而对于机械系统,在不确定其自身工作状态时,使可靠性和持续性依旧能够保存是一项十分值得研究的工作。因此,需要通过借助相关数据和试验结果,才能更加精准地确保机械系统可以在不确定工作状态情况下,保持系统自身稳定性与可靠性。
1 非确定工作状态下机械系统可靠性评估方法
1.1 故障树与贝叶斯网络
(1)T-S 故障树。随着机械设备运行负载逐渐加剧,处于非确定工作状态时,其性能退化会逐渐加剧,也就意味着,该设备的使用年限在重载压力下被缩减,尤其是在特别复杂的工况下,零部件退化现象呈现出多样化的复杂特征,为避免上述情况逐渐加剧,要进一步对机械系统的可靠性做好全面评估。T-S 故障树基于传统的故障树并在此基础上增加了一系列IF-THEN 规则的T-S门结构,通过此代替逻辑门对系统中各零部件的磨损情况进行全面分析。(2)贝叶斯网络。利用BN 中各个节点之间的因果递进关系,将已知节点的先验概率作为基础,同时基于贝叶斯概率公式对机械系统零部件节点或者液节点的后验概率,从而完成对机械系统可靠性的综合评估。BN 具有描述多故障状态的特征,也具有描述非确定工作状态下的功能,能够表达系统各零部件之间的不确定逻辑关系,进而对系统中存在的故障问题或异常问题进行诊断分析,得出零部件的重要度计算公司,从而找出影响系统可靠性的关键因素。(3)基于T-S 故障树构建贝叶斯网络。BN 模型的构建主要有两个部分,其一是确定BN 的DAG 结构,其二是确定BN 的CPT 参数。在构建的过程中,需要将T-S 故障树中的事件与BN 的相应节点形成对仗,然后根据T-S 门表示T-S 故障树中存在的逻辑关系相应的节点。根据事件发生的概率做好排序和排列,通过概率知识转化为对应节点的先验信息,其流程图如图1 所示。
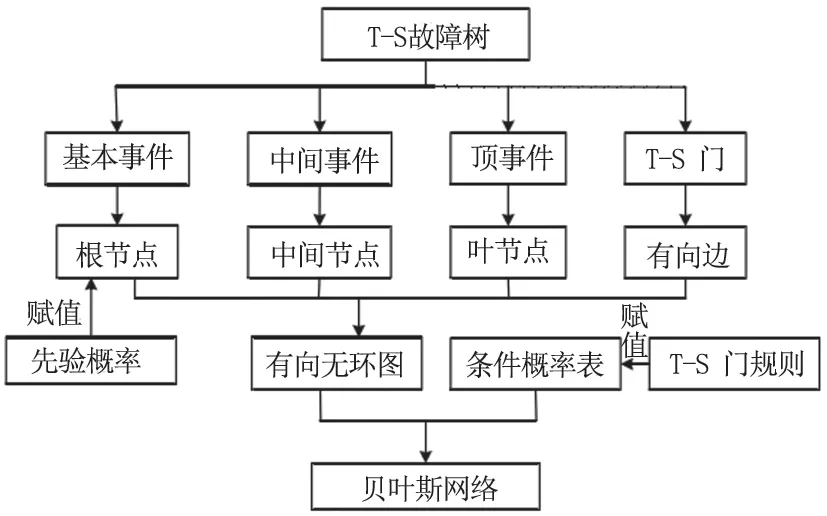
图1 T-S 故障树映射为BN 流程图
1.2 构建模糊多态贝叶斯网络
(1)模糊BN 节点的描述。机械系统在运行过程中,由于系统结构相对复杂,运行工况和负载也会随着工作状态的切换而变化,都会造成对系统可靠性产生影响。对系统先验信息了解不足,无法明确了解某些关键零部件的准确故障率。采用模糊子集的方式对系统中各事件、零部件在各种不同的故障状态下进行描述,将模糊节点集合添加到BN 的连续节点中,能够有效分析出对系统可靠性的重要影响因素,可提高故障概率的识别度与精确度。(2)构建区间模糊多态BN 的DNG 和CPT。所构建的区间模糊多态BN 与传统的BN 在结构上基本相似,其中新增的DAG 是由T-S 故障树转化而来的,且与传统的T-S 故障树结构两相对应,其结构如图2 所示。
图2 区间模糊多态BN 的DAG
T-S 故障树转化为贝叶斯网络,是在特定的情形下产生的,需要与专业学者总结的相关理论和多源信息融合下所归纳的多种故障状态和系统零部件故障关系的逻辑关系模糊性进行综合考量。应根据T-S 门的规则,引入区间模糊子集,建立区间贝叶斯网络的CPT。
1.3 基于区间模糊多态BN 的系统可靠性评估
(1)叶节点故障状态模糊子集。利用区间模糊子集表示的函数对机械系统可靠性进行研究,在架设状态下,已知全部根节点故障状态下发生的概率,根据BN消元推理算法能够推断出系统设备属于什么运行情形下,零部件的可靠性最高。(2)根节点区间模糊重要度。运用叶节点故障状态模糊子集的函数关系对跟节点区间模糊重要度进行综合评估,当系统故障状态为恒定值时,叶节点的模糊重要度可形成一个完整的函数关系。(3)根节点后验概率。结合BN 的诊断原理,采用贝叶斯定理和相关学者总结的推理知识,可以通过机械系统移植系统叶节点各故障状态发生时,系统的运行状态总结出其故障发生的频率,并根据根节点的函数关系恒等式求解根节点后验概率。
2 可靠性建模
2.1 机械零件失效率数据模型
产品可靠性是设计出来的,机械产品系统的可靠性也不例外。机械系统运行的效率如何与其内部零部件的损耗情况、耐腐蚀程度以及抗疲劳性息息相关,当零件承受单一负荷处于失效模式单一时,其强度应力模型可以很好地对机械系统运行现状进行描述。为全面提高生产效率,促进工业企业可持续健康长远发展,机械设备通常运行时间远远超过其所能承受负荷,产生这种状况的影响因素并不是单一存在的,在高负荷的运载状态下,零部件受损比较严重,加上外部环境对机械设备的腐蚀作用以及温度等因素影响。在这个过程中,机械系统会呈现出非运行状态的模式,其具有多样化的特征,即当机械系统处于多强度多应力的情况下,其描述的情形与现实状况不相吻合,存在一定的局限性。NSWC 标准采用数学模型对机械设备内部零部件的使用寿命进行评估,将此作为基础并借助可靠性方程式对系统运行不同状态下的参数和环境进行综合考虑,对机械设备零部件的可靠性指数进行评估。通过可靠性方程对机械零部件使用寿命进行预计,具有一定的局限性。在假设条件下,已知系统设备零部件的应力水平,基于基本失效率以及设备使用环境变化导致的运行状态发生变化,通过引入修正因子能够对失效现行进行分析、推理以及判断,同时可加以校正,能够有效减低故障发生概率。根据零件失效率模式预估的结果可得知,当零件受到的负荷强度保持在恒定状态下时,零件失效率也属于恒定;当零件处于不同的载荷条件以及不同的工作状态下时,零件失效率会根据情况的变化发生改变。
2.2 机械系统可靠性模型
机械系统的故障模型和零部件实效模型同样具备多样化的特点,结合了机械工作条件的不确定性等因素影响,以及工作负荷的复杂性和机械零部件间的相互作用的复杂新特点。若在可靠性模型建立方法中充分考虑这些危险因子,则采用其方法所建立的可靠性模型将会非常复杂,且有效性也相对较小。为了进一步使模拟系统更有利于机械系统可靠性模型,需通过实验数据加以验证。假设的前提条件有5 个部分:第一,机械系统中的所有零件都彼此独立,所有零件之间任何一次失效都没有影响系统的正常工作;第二,当机械系统处在非确定工作状态,系统和零件工作的条件保持恒定时,失效率保持恒定状态;第三,零件和零部件间的工作时间失效率和零件时间失效率没有直接关系;第四,没有考虑人员的使用对系统可靠性产生的影响;第五,假设在交变载荷的作用下,零件和系统的可靠程度模型不会改变。
根据零部件的失效率运行算式来看,设备的受载荷应力和设备装置所处条件等因素确定了零件的受载荷应力程度和环境参数。在现代机械设计生产条件变化中,零件的失效率也将出现相应的改变。根据零件可靠性预测模型的变量理论可知,由于机械系统工作状态具有极强的随机性,导致零部件的加工工艺、转速、切削速度与功率等大不相同,使得不同零部件之间所受载荷与工作状态之间的关系具有明显的随机性特征。零件与系统之间的失效率具有较大随机性,因而不能用确定函数关系算式对其进行描述,失效率却随时间变化而变化,究其根本,对系统状态之间的关系难以定性。
2.3 某重型机床主轴传动系统结构
根据所选取的某个重型机械设备对主轴传动系统的可靠性进行解读表明,设备运行状态变化的情况下,系统可靠性也会发生变化。该设备的主轴系统主要由五级齿轮减速传动机构、换挡辅助机构、直流无极变速主轴电机、联轴器组成。各系统元件在设备正常运行时相互配合,由主轴电机发出动力,再将动力传输到联轴器位置,使其与主轴箱输入轴系统进行连接,然后通过五级齿轮传动部件将动力传输至输出轴位置。当主轴箱处于低速的运动状态时,3 轴大滑轮齿轮能够维系正常运行,当设备运行速度不断加快,超过恒定标准达到高速度时,3 轴小滑轮会移动到齿轮位置,依旧是正常运行的工作状态。由于该重型机床设备各个系统元素之间的功能特征具有较大差异性,对机械系统所产生的影响和作用也大不相同,对系统的可靠性具有重要影响。从主轴箱动力传力角度分析,需要重点关注轴承、齿轮以及轴等3个类型的零件。
2.4 主轴传动系统可靠性建模
某重型机床机械设备主轴传动系统状态用功率、转速、转矩以及工作档位等参数进行表示,当功率P 处于以下范围时(0 <P ≤180kW)其可靠性建模图谱如图3所示。
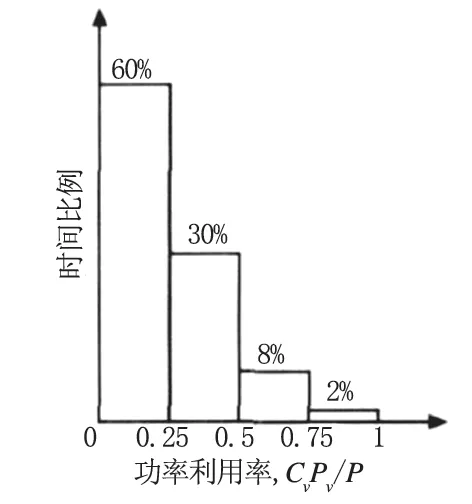
图3 机床功率利用图谱
当转速N 处于以下内0.33 ≤N ≤60r/min,转速工作时间分配谱如图4 所示。
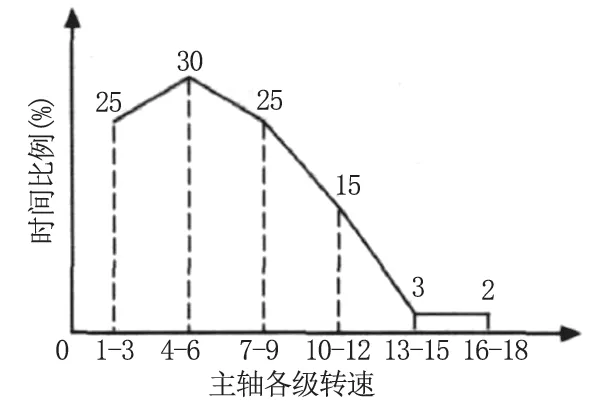
图4 转速图谱
根据NSWC 标准可以得到该机床各个零部件的失效率模型,根据以上图谱状况的向量关系与约束条件及其传动系统结构和工作原理,可计算出系统齿轮状态向量为:
2.5 主轴传动系统可靠性分析
由机械系统状态向量与系统失效率之间的解析关系分析,可以得知系统独立特征量与失效率之间的关系。当机械系统处于非确定性工作状态下,零部件失效率恒定。对每个系统状态点可得到的特定失效率进行分析,从而能够找到系统失效率较高时,主轴传动系统的可靠性模型,以便于避免在工作期间造成失效现象,当系统处于约束条件下,主轴传动系统功率、转速与系统之间的关系如图5 所示,由数据图分析可知,应尽量避免使系统处于长时间运行状态。

图5 功率转速与系统失效率关系图
3 结语
综上所述,不同工作载荷下机械系统所呈现出的失效率不尽相同,经过实验验证计算和分析系统可靠性程度和装置所处的环境有很大的关系。通过构建设备零件失效率数学模型,获得了零件失效率与其工作状况间的向量联系,从而确定设备失效率受设备工作状况的影响较大。
