基于IGWO-BP神经网络的锂离子电池SOC估计

2023-10-05于仲安邵昊晖陈可怡

电源技术 2023年9期

于仲安，邵昊晖，陈可怡

(江西理工大学电气工程与自动化学院，江西赣州 341000)

由于传统能源的短缺以及对环境保护的客观要求，新能源汽车成为了未来汽车的发展方向，2020 年中国新能源汽车的总销量达到136.7 万辆[1]。在新能源汽车中，电池管理系统(BMS)在车辆行驶过程中发挥着极为重要的作用。而BMS中对于锂电池荷电状态(state of charge，SOC)的准确估计是一个重要的环节，因为SOC的估计精度对于车辆的续航里程影响很大。目前国内外对锂电池的SOC估算方法主要有常规法、基于电池模型的方法和数据驱动法等。

杨文荣等[2]提出通过卡尔曼滤波法得到电池模型的实时开路电压(OCV)，再通过SOC-OCV的关系曲线得到电池SOC，实现了较好的估算效果。欧阳佳佳等[3]提出了一种改进的安时积分法，能够比较准确地估算初始的SOC，进而提高SOC的估计精度。董祥祥等[4]提出将改进的Sage-Husa 自适应滤波算法与无迹卡尔曼滤波结合形成一种新的AUKF 算法，对系统的噪声特性进行估计和修正，从而提高SOC的估计精度。方磊等[5]提出一种基于模糊控制的扩展卡尔曼滤波算法，减小了由观测方程误差造成的SOC估计误差，提高了SOC的估计精度。Zhang Li 等[6]提出最小二乘支持向量机模型来描述锂离子电池的动态特性，再采用无迹卡尔曼滤波(UKF)估计电池的SOC，实现了比较高的估计精度。Hicham Ben Sassi 等[7]提出基于卡尔曼滤波的观测器和滑模观测器来估计SOC，有着不错的估计精度。

考虑到灰狼优化算法能够寻求全局最优解的特点，通过优化BP 神经网络的权值和阈值来解决单一的BP 神经网络容易陷入局部最优的缺点，因此本文提出利用改进灰狼算法优化BP 神经网络的联合算法来进行锂离子电池的SOC估计。

1 BP 神经网络估计电池SOC 的模型建立

BP 神经网络最大的优点在于具有很强的非线性映射能力，是目前应用比较广泛的人工神经网络。BP 算法包括前向传播和误差反向传播两个过程，前向传播是由输入信号通过隐含层作用于输出层节点，产生输出信号，如果输出信号的值与期望值相差太大，则进入误差反向传播过程，通过调整网络的权值和阈值来达到减小误差的目的。基于BP 神经网络的锂电池SOC估计模型如图1 所示。

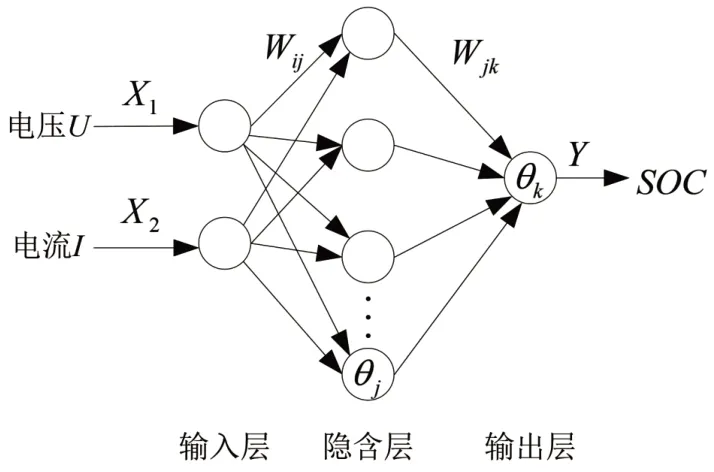
图1 基于BP神经网络估计电池SOC模型

图1 中：Wij为输入层和隐含层之间的权值；θj为隐含层的阈值；Wjk为隐含层和输出层之间的权值；θk为输出层的阈值。本文选择以电池的电压和电流两个参数作为BP 神经网络的输入，电池的SOC作为神经网络的输出Y[8]。于是将输入层节点数n确定为2，输出层节点数l确定为1。根据经验公式计算隐含层节点的个数：m=+a，其中a为[1,10]之间的常数，经过多次仿真实验对比，将隐含层节点数m确定为12 时，仿真效果最佳。

2 IGWO-BP 神经网络的模型建立

2.1 标准的灰狼优化算法

标准灰狼优化算法(grey wolf optimization，GWO)是由澳大利亚学者Seyedali、Mirjalili 等提出的[9]。该算法模拟了自然界灰狼的领导层级和狩猎机制。在狼群中，灰狼被分为四个等级，其中最优灰狼α 负责狼群中的各项决策事务，次优灰狼β 负责协助α 进行决策，当α 狼的位置出现空缺时，β 狼将接替α 狼的位置。第三优灰狼δ负责听从α 狼和β 狼的命令，最底层的灰狼ω负责平衡狼群的内部关系。灰狼的社会等级制度如图2 所示。

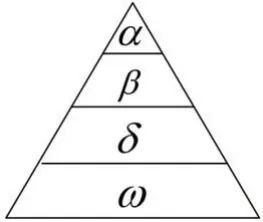
图2 灰狼的社会等级制度

灰狼捕食猎物的模型可以定义如下：

式中：D为灰狼与猎物的距离；t为迭代次数，tmax为最大迭代次数；XP(t)为猎物的位置，X(t+1)为第t+1 次迭代时灰狼的位置；a为收敛因子，随着迭代次数从2 线性减少到0；A和C分别为系数向量。式(2)是灰狼的位置更新公式。

灰狼算法中根据α、β、δ 三头狼的位置捕食猎物：

式(3)表示其他狼ω 与α、β、δ 狼的距离，式(4)表示根据α、β、δ 狼的位置更新其他灰狼的位置，式(5)表示ω 狼的最终位置。

2.2 改进的灰狼优化算法

2.2.1 Tent 混沌映射初始化种群

灰狼优化算法利用随机的数据作为初始的种群信息，很难保留种群的多样性，会导致算法的寻优结果较差。然而混沌运动具有规律性、遍历性的特点，能够保留种群的多样性，同时还能提高算法的全局搜索能力。因此加入Tent 混沌映射产生初始种群，可以用来增加种群个体的多样性。Tent 混沌映射分岔图如图3 所示，其中横坐标u表示种群的范围，纵坐标X表示种群的初始值。由图可知Tent 映射的遍历具有均匀性和随机性，能够使算法跳出局部最优解，从而维持种群的多样性，同时提高全局搜索能力。

图3 Tent混沌映射分岔图

Tent 映射的表达式为：

式中：u为[0,1]之间的数，当u=1/2 时，Tent 映射具有典型的形式，此时得到的序列有比较均匀的分布，对不同的参数也有近似一致的分布密度。

2.2.2 非线性参数控制策略

根据式(1)可知，标准灰狼优化算法在迭代过程中，当a的值从2 线性下降到0 时，对应的A的值也在区间[－a,a]内变化。当 |A|＞1 时，灰狼群体将增大搜索范围，找到更优的解；当 |A|＜1 时，灰狼群体将缩小搜索范围，在局部范围内进行寻优。A的值是随着收敛因子a的变化而变化的，也就是灰狼优化算法的全局和局部开发能力取决于a的变化，因此引入一种新的非线性控制参数：

式中：aini和afin分别为控制参数a的初始值和最终值；t为当前迭代次数；Tmax为最大迭代次数。

为了证明本文设计的控制参数的有效性，选取其他文献中的控制参数进行对比。标准灰狼算法的线性控制参数表达式如式(8)所示，滕志军等[10]提出的非线性控制参数表达式如式(9)所示，王正通等[11]提出的非线性控制参数表达式如式(10)所示。

对4 种控制参数进行仿真绘图，如图4 所示，由图可知本文设计的A值前期递减速度慢，能够增加全局搜索能力，避免算法陷入局部最优；后期A值递减速度快，增加局部搜索能力，同时加快算法的寻优速度。

图4 4种控制参数动态变化曲线

2.2.3 引入粒子群思想

在粒子群算法中，利用粒子自身经历的最优位置和群体经历过的最优位置来更新粒子当前的位置，实现了个体与种群之间的交流[12]。本文通过引入粒子群算法中粒子位置更新的思想，将灰狼个体经历过的最优位置引入到公式中来，新的位置更新公式为：

式中：X(t+1)为t+1 时刻灰狼的位置；c1为社会学习因子，c2为认知学习因子，c1表示个体最优值对算法搜索能力的影响，c2表示群体最优值对算法搜索能力的影响；r3和r4为[0,1]之间的随机数；Xibest为灰狼个体经历的最优位置；ω1、ω2、ω3为权重系数，用来调节α、β、δ 狼对灰狼个体位置更新影响的权重比例，这能够提高算法的全局搜索和局部搜索能力。

2.3 IGWO 优化的BP 神经网络算法

单一的BP 神经网络收敛速度慢，且容易陷入局部极小值，不能获得全局最优解。本文利用改进后的灰狼优化算法具有寻优能力强的特点，来优化BP 神经网络的权值和阈值，避免网络陷入局部最优。首先将灰狼的位置信息进行编码，用来存放BP 神经网络的权值和阈值，采用均方误差作为网络的适应度函数，适应度值越小说明灰狼的适应性越好，预测值与期望值相差不大。灰狼在进行位置更新的同时也更新了BP 神经网络的权值和阈值。改进的灰狼算法优化BP 神经网络的步骤如下。

步骤1：利用Tent 混沌映射对灰狼种群的位置进行初始化，以及a、A和C。

步骤2：把灰狼的位置信息进行编码，然后赋予BP 神经网络，并计算适应度值，保存适应度最好的α、β 和δ狼。

步骤3：根据公式(3)、(4)、(11)和(12)更新灰狼的位置，并根据公式(7)更新a、A和C的值。

步骤4：判断算法是否达到最大迭代次数或达到预设的精度，如果没有则继续进行迭代，否则输出最优灰狼位置信息赋予BP 神经网络，得到初始最优权值和阈值。

步骤5：对BP 神经网络进行训练，进行仿真预测，得到输出结果。

IGWO-BP 联合算法流程如图5 所示。

图5 IGWO-BP神经网络联合算法流程

3 实验仿真与结果分析

3.1 实验数据的预处理

实验数据选用NASA 公司的三元锂电池在UDDS 工况下的放电数据，将UDDS 工况下电池的电压和电流作为模型训练的输入数据，电池的SOC作为模型训练的输出数据。测试工况数据集共有12 315 组数据，从中随机挑选900 组数据，其中700 组数据用来训练，200 组数据用来测试。部分数据如表1 所示。

表1 锂电池部分充放电数据

使用Sigmoid 函数作为激活函数。将数据进行归一化处理：

式中：Xi、Xinor分别为样本值及归一化后的值；Xmax、Xmin分别为样本数据中的最大值和最小值。

3.2 仿真与结果分析

为了验证经过改进灰狼算法优化后的BP 神经网络估计SOC的效果要优于单一的BP 神经网络，在MATLAB 中进行仿真预测实验。仿真实验结果如图6 所示，图中绿色“+”表示期望输出值，黑色实线表示网络预测输出值。从图6 可以看出，IGWO 优化后的BP 神经网络相比单一的BP 神经网络具有更好的预测效果。

图6 网络输出值与期望输出值对比

从图7 可以看出，IGWO-BP 神经网络的预测误差绝大部分保持在2%以内，最大误差为3.34%，而BP 神经网络的预测误差大部分在6% 之内，最大误差达到了9%，明显大于IGWO-BP 神经网络。由于SOC估计误差有正有负，而平均绝对误差能够避免误差相互抵消的问题，可以准确反映实际预测误差的大小，因此本文选择平均绝对误差作为性能指标。BP 神经网络估计锂电池SOC的平均绝对误差为6.39%，而基于IGWO-BP 神经网络估计锂电池SOC的平均绝对误差为1.45%，相比于BP 神经网络平均绝对误差减少了4.94%。经过仿真实验表明，利用改进灰狼算法优化后的BP 神经网络在预测电池的SOC时表现出了更好的准确性。