中国省域粮食产量影响因素分析
2023-10-04和亚晴李治
和亚晴 李治
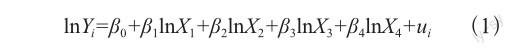
摘要:粮食生产水平对一个地区和一国的经济发展具有重大的战略意义。文章运用Eviews 8.0软件构建了一个多变量的双对数模型,利用方差膨胀系数、异方差(怀特检验)、自相关(BG检验)等计量经济方法对中国31个省市区的粮食生产进行了统计分析。结果表明,各地区粮食播种和有效灌溉面积每增加1%,其粮食总产量分别增加0.798 969%、0.257 526%。最后,在实证研究的基础上,结合中国目前面临的粮食生产问题,提出了相应的政策建议。
关键词:多元线性回归;粮食产量;最小二乘法;Eviews 8.0
中图分类号:F326.11 文献标志码:A DOI:10.16465/j.gste.cn431252ts.20230303
Analysis of factors influencing provincial grain production in China
He Yaqing, Li Zhi
(School of Economics and Trade, Henan University of Technology, Zhengzhou, Henan 450001)
Abstract: The level of grain production in China is of great strategic importance to the economic development of a region and a country. In this paper, a multivariate double logit model was constructed using Eviews 8.0 software, and statistical analysis of grain production in 31 provinces was conducted using econometric methods such as the variance inflation coefficient, heteroskedasticity (Whites test) and autocorrelation (BG test). The results showed that for every 1% increase in grain sown and effective irrigated area in each region, the total grain production in each region increased by 0.798 969% and 0.257 526%. Finally, on the basis of the empirical study, combined with the current grain production problems in China, the corresponding policy recommendations were put forward.
Key words: multiple linear regression, grain production, least squares method, Eviews 8.0
黨的二十大报告提出,全方位夯实粮食安全根基,牢牢守住“18亿亩耕地红线”,确保中国人的饭碗牢牢端在自己手中。现在国际局势持续动荡,自然灾害肆虐,粮食产量、安全问题再次成为了人们关注的问题。粮食生产是粮食安全的基础,但最近几年,我国粮食生产受到耕地面积退化和化肥过量施用导致环境污染等问题的严重威胁[1]。改革开放以来,我国各地区的粮食产量出现过多次波动,这是因为粮食产量受到众多因素的影响。基于此,本文选取了我国31个省市区2020年相关粮食产量的截面数据来探究各地区粮食产量的影响因素,通过分析回归模型方程,并结合现在粮食生产所面临的诸多问题,提出增加粮食产量的建议。
1 相关文献回顾
粮食是人民生存之本,经济发展之柱,对稳定社会、经济具有重要的作用。影响粮食生产的因素有很多,目前国内学者用不同的方法和模型来进行探究,主要有粗糙集理论、对数均值迪氏指数法、主成分分析法和多元线性回归模型4种。欧阳浩等[2]选取1996—2012年的数据,利用粗糙集理论对广东省粮食产量的影响因子进行了分析,研究发现化肥用量、水库总量和人均经营耕地面积对粮食产量影响较大。周志刚等[3]采用对数均值迪氏指数法来分析。结果表明,各个影响因子具有阶段性,但总的来说,播面单产和复种指数表现的是增长效应,且播面单产对粮食增长的贡献比复种指数的大;种植结构和耕地面积表现的是减量效应,且种植结构变化带来的粮食减产要比耕地面积变化带来的粮食减产多得多。李心慧等[4]采用主成分分析法定量分析了影响粮食单产的主要因素,发现塑料薄膜的使用量、农用机械总功率、农村用电量、化肥施用量(折纯法)和有效灌溉面积推动了河南省粮食单产的增加,农业生产资料价格指数对粮食单产的提高有一定的阻碍作用,而农村从业人口的减少对粮食单产的增加并没有特别明显的作用。谷宝同等[5]从粮食生产视角,基于1999—2017年的时间序列数据,选取中国粮食的总产量为被解释变量,粮食播种、有效灌溉面积、农业机械总功率、化肥施用量(折纯法)和受灾面积5个解释变量,建立了多元线性回归模型,采用计量经济学方法对其进行检验并修正,最后得到中国粮食产量与5个解释变量之间的定量关系。李苗[6]选取时间序列数据,建立多元双对数模型,通过协整分析,得出粮食产量与各影响因素之间的协整关系,并发现粮食产量和粮食播种面积、化肥施用量(折纯法计算)以及有效灌溉面积之间存在着一种长期均衡的关系。张涛等[7]运用多元线性方程分析了山东省粮食产量增长因素的贡献值,选择运用主成分分析法解决多重共线问题,得出影响粮食单产因素方程并为保障粮食安全提出建议。
根据相关文献回顾可知,粮食产量的影响因素和分析方法有很多,在实证分析部分运用最多的是多元线性回归模型,且大多运用时间序列数据。基于此,本文在学者们研究的基础上,选取我国31个省市区的相关截面数据,建立多元双对数线性模型来分析我国省域粮食产量的影响因素,参数估计采用最小二乘法,并对模型进行检验并修正。
2 实证分析
2.1 变量选取和数据来源
有关粮食产量的影响因素有很多,通过查阅以往文献,综合学者们的研究,选取粮食作物播种面积(lnX1)、有效灌溉面积(lnX2)、受灾面积(lnX3)、农村用电量(lnX4)作为解释变量,各省域的粮食产量(lnY)作为被解释变量。研究数据来自《中国农村统计年鉴2021》。
2.2 模型设定、参数估计及模型检验
2.2.1 总体回归模型設计
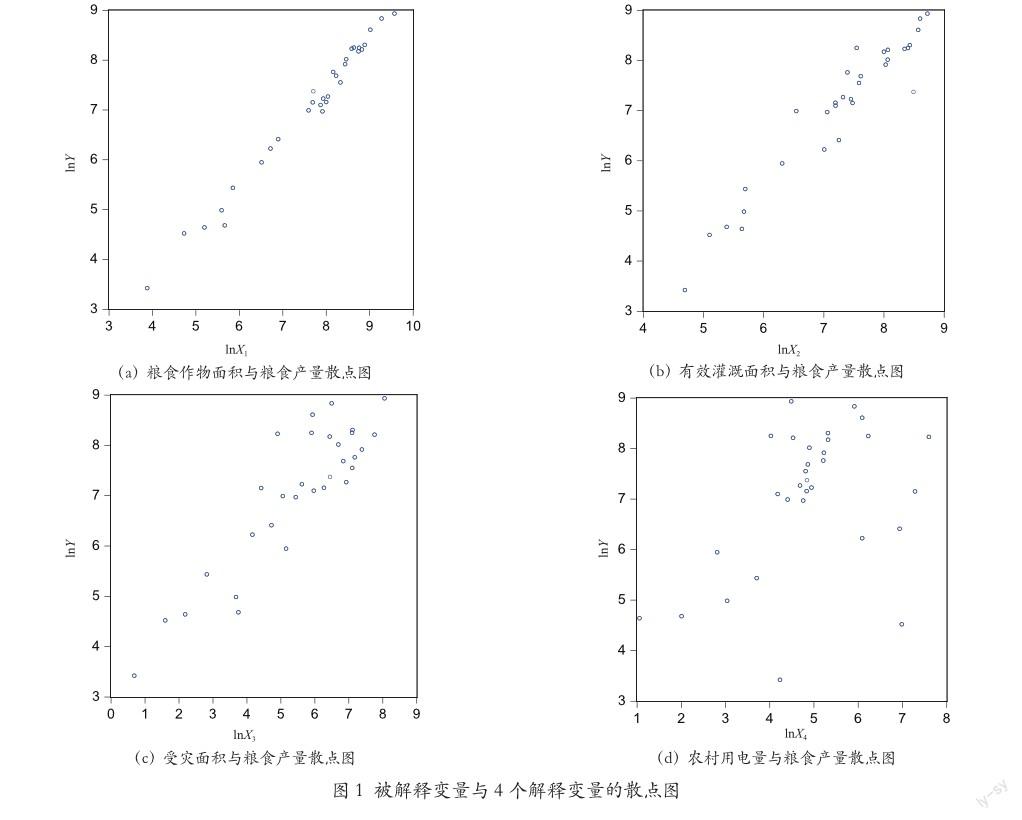
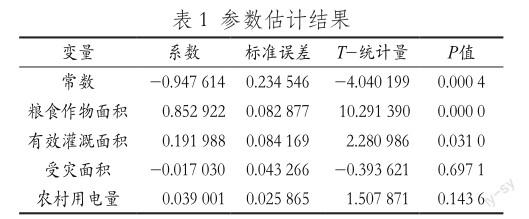
被解释变量与4个解释变量的散点图,见图1。由图1可知,粮食作物面积(lnX1)、有效灌溉面积(lnX2)、受灾面积(lnX3)、农村用电量(lnX4)分别与各省域粮食产量(lnY)之间呈线性关系,故建立双对数线性回归模型: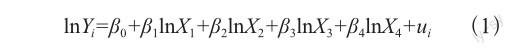
2.2.2 模型参数估计及检验
将被解释变量与解释变量的数据代入回归模型中,利用Eviews 8.0软件进行最小二乘法回归,结果见表1。
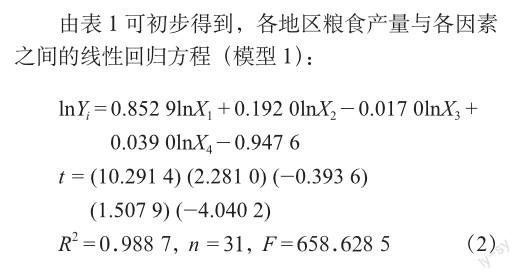
(1)模型1经济意义检验:lnX1、lnX2、lnX4 3个解释变量的相关系数为正值,lnX3的相关系数为负值,符合经济意义。
(2) 模型1统计推断检验:给定显著水平0.05。根据表2可知,lnX1、lnX2对各地区粮食产量的影响显著;lnX3、lnX4对各地区粮食产量的影响不显著。方程整体显著性F检验的P值为0,即方程总体显著。调整后的可决系数R2=0.988 7,接近于1,表明样本回归线对样本点的拟合程度较高。
(3)多重共线检验:采用方差膨胀因子法来检验,结果见表2。
当方差膨胀因子≥10时,认为该解释变量与其余解释变量之间存在严重的多重共线。由表2可知,lnX1、lnX2的方差膨胀因子>10,表明该模型存在严重的多重共线。
2.2.3 多重共线修正与检验
(1)多重共线修正:对于多重共线的修正,本文采用的是逐步回归法[8]。先让被解释变量与每个解释变量回归,可以得出一元线性回归模型中每一个变量的T检验值均小于0.05。通过对比可决系数,最终决定选取变量lnX1作为逐步回归的基础。先建立lnY与变量lnX1的一元线性回归模型,在基础上依次加入变量lnX2、lnX3、lnX4。在加入变量的过程中发现,加入变量lnX3后导致变量T检验不过,而加入lnX2、lnX4都是可以通过T检验,但经过对比后,发现加入变量lnX2的方程调整后的可决系数最大,所以判定lnY与lnX1、lnX2的二元线性回归模型是最优的。在这个基础上再依次加入lnX3、lnX4,加入之后进行回归得知可决系数虽然有所增大但会导致参数的T检验不显著,所以剔除变量lnX3、lnX4,留下变量lnX1、lnX2。经过引入—检验—剔除后进行回归分析,结果见表3。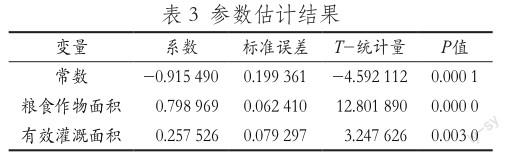
由表3得到模型2: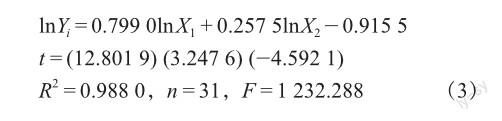
(2)模型2经济意义检验:在其他解释变量不变的情况下,粮食作物播种面积(lnX1)每增加1%,各地区粮食产量会增加0.799 0 %;有效灌溉面积(lnX2)每增加1%,各地区粮食产量会增加0.257 5%,均符合经济意义检验。
(3)模型2统计推断检验:给定显著水平0.05。根据表3数据可知,lnX1、lnX2 T检验P值<0.05,即粮食作物播种面积和有效灌溉面积两个解释变量对各地区粮食产量的影响是显著的。方程整体显著性F检验的P值为0,说明方程总体显著。调整后的可决系数R2 = 0.988 0,接近于1,表明了样本回归线对样本点的拟合程度很高。
(4)模型2多重共线检验:采用方差膨胀因子检验,结果见表4。
由表4可知,方差膨胀因子均小于10,所以认为该模型不存在多重共线。
(5)模型2异方差检验:采用怀特检验,结果见表5。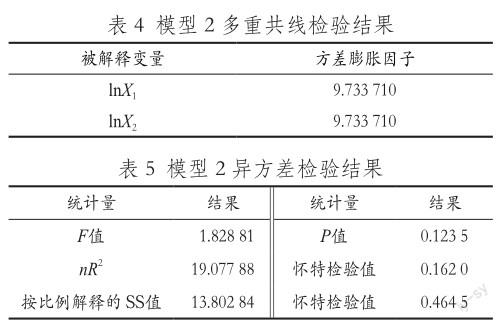
由表5可得,怀特检验的P值>0.05,因此拒绝原假设,该回归模型不存在异方差。
(6)模型2自相关检验:采用BG检验,依次检验一阶、二阶、三阶和四阶,结果见表6。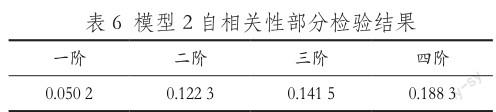
由表6可知,各个阶数P>0.05,故该模型2不存在自相关。
2.2.4 实证分析结果
經过一系列的修正和检验,最终得出模型2能够通过经济意义、统计、多重共线、异方差和自相关检验。由最终回归方程lnYi = 0.799 0 lnX1 + 0.257 5 lnX2 - 0.915 5得出:① 粮食播种面积与省域粮食产量呈现出较为明显的正向相关关系,即粮食播种的面积越多,当地的粮食产量越高。而且当其他变量保持不变时,粮食播种面积增加1%时,当地的粮食产量就会增加0.799 0%。② 有效灌溉面积也与当地的粮食产量呈现出明显的正相关关系,即有效灌溉面积越多,当地的粮食总产量会相应地增加。而且当其他变量保持不变时,有效灌溉面积增加1%时,当地的粮食产量就会增加0.257 5%。
3 对策建议
根据实证分析得出的结果,再结合我国目前粮食生产所遇到的一系列问题,为了提高我国各地区的粮食产量提出以下建议。
(1)保护粮食作物播种面积。粮食作物播种面积是对各地区粮食产量影响最为显著因素,各级政府部门有必要把抓粮食生产的工作放在首位,同时要坚决守住“18亿亩耕地红线”,防止耕地变成非农用地,合理地调整结构性矛盾,千万不能打着发展特色农业和现代农业的旗号大面积不合理种植高效经济作物[9]。另外,在保护原来耕地面积的基础上,还可以考虑适当地把“18亿亩耕地红线”上调。增加耕地面积可以提高粮食产量,从而减轻粮食供给压力[10]。
(2)加强农田水利基础设施建设。有效灌溉面积是对各地区粮食产量影响的第二大显著因素,对于粮食产量的增加起到了重要的推动作用。水是农业的生命之源,是农业生产的命根子,农业与水不可分离。若水资源短缺,会影响到农业灌溉,从而导致粮食减产。所以更应该加大对农田水利的资金投入,对农田水利设施的设计、建造与运行、使用和维护等每一个阶段进行有效治理,来全面提升农田水利设施服务国家粮食安全的能力和水平。
(3)科学合理、正确使用化肥。无可厚非,化肥在增加粮食产量方面发挥了巨大的作用。但施肥过量会导致粮食减产,不施肥粮食也会减产,所以必须要正确、合理使用化肥。可以考虑以下做法:增施微生物菌肥,改进施肥方式,把握最佳的施肥时间等。
参 考 文 献
[1]李昊儒,毛丽丽,梅旭荣,等.近30年来我国粮食产量波动影响因素分析[J].中国农业资源与区划,2018,39(10):1-10+16.
[2]欧阳浩,戎陆庆,黄镇谨,等.基于粗糙集方法的广东省粮食产量影响因素分析[J].中国农业资源与区划,2014,35(6):100-107.
[3]周志刚,郑明亮.基于对数均值迪氏指数法的中国粮食产量影响因素分解[J].农业工程学报,2015,31(2):1-6.
[4]李心慧,朱嘉伟,王旋,等.基于主成分分析的河南省粮食产量影响因素分析[J].河南农业大学学报,2016,50(2):268-274.
[5]谷宝同,朱家明,龚量.基于多元线性回归的中国粮食产量影响因素实证分析[J].哈尔滨师范大学自然科学学报,2020,36(3):37-42.
[6]李苗.新时代下我国粮食产量的影响因素分析[J].价值工程,2019,38(14):150-152.
[7]张涛,田东林,杨进敏.基于多元线性回归的山东省粮食生产影响因素分析[J].粮食科技与经济,2021,46(2):16-21.
[8]段其政,田佳辰.黑龙江省粮食产量的影响因素分析[J].粮食科技与经济,2020,45(12):52-55.
[9]周娜娜,饶志坚.基于灰色关联分析的云南省粮食产量影响因素分析[J].农业与技术,2022,42(15):164-167.
[10] 刘同山.新时代保障国家粮食安全的内涵、挑战与建议[J].中州学刊,2022(2):20-27.
