压电陶瓷驱动定位平台自适应伪逆控制算法及计算机仿真研究

吴盛彬

摘 要：本文以压电陶瓷驱动微定位平台为研究对象，针对压电陶瓷这种智能材料驱动器中固有的迟滞非线性，构建改进型Prandtl-Ishlinskii（MPI）迟滞模型，提出一种含伪逆补偿器的自适应控制方法，避免了直接求解复杂的迟滞逆模型，通过对设计的临时控制信号应用搜索算法，建立一种近似控制信号的在线搜索机制。最后，通过MATLAB/Simulink对比仿真分析表明了该控制方法的有效性。

关键词：压电陶瓷；微定位；自适应；伪逆

1 前言

压电陶瓷驱动的微定位平台具有低耗能、驱动力大、定位精度高、响应速度快等优点，目前被广泛应用于高精度微纳米级加工制造领域[1]。但这种智能材料驱动器存在固有的迟滞非线性，而迟滞具有不可微分、多值映射、非平滑及记忆性的特点，严重限制了其应用[2]。

如何获得最佳的定位精度，最小化智能材料中存在的迟滞现象是一巨大挑战。前馈逆补偿方法原理简单易懂，对迟滞的处理非常有效[3]，但只有在逆模型存在且所构建的逆模型十分精确才能表现出良好的性能。此外，所构建的估计模型和实际迟滞之间总是存在建模误差。因此，迟滞逆补偿模型将产生补偿误差且会增大控制系统的跟踪误差，设计一种伪逆补偿的控制方法是智能材料驱动微定位平台控制的难点。

2 压电陶瓷驱动微定位平台迟滞非线性建模

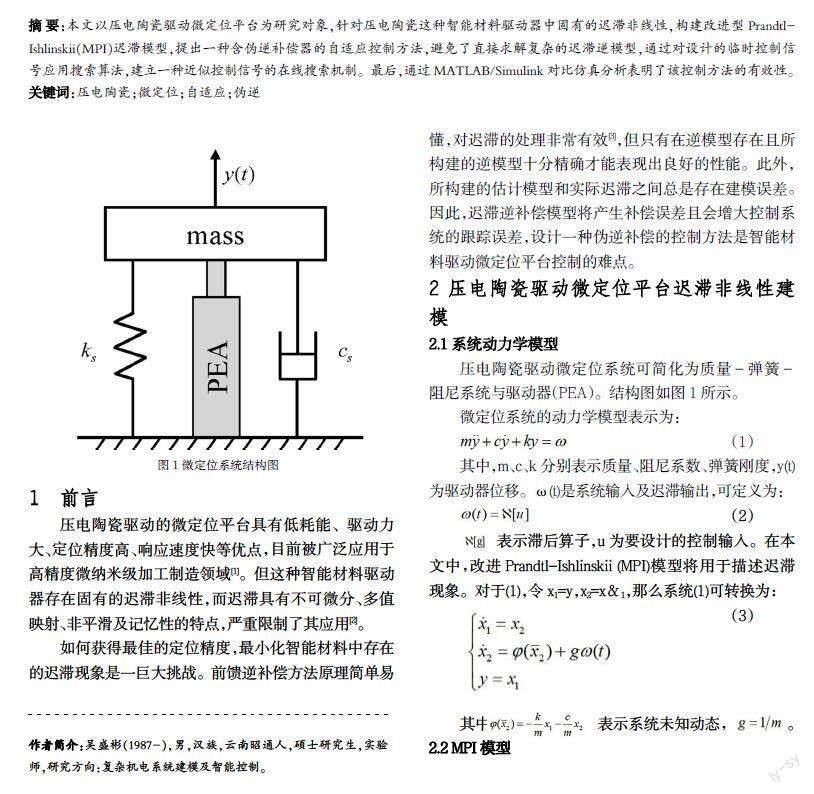
2.1系统动力学模型

压电陶瓷驱动微定位系统可简化为质量－弹簧－阻尼系统与驱动器（PEA）。结构图如图1所示。

微定位系统的动力学模型表示为：

（1）

其中，m、c、k分别表示质量、阻尼系数、弹簧刚度，y（t）为驱动器位移。ω（t）是系统输入及迟滞输出，可定义为：

（2）

表示滞后算子，u为要设计的控制输入。在本文中，改进Prandtl-Ishlinskii （MPI）模型将用于描述迟滞现象。对于（1），令x1=y，x2=x＆1，那么系统（1）可转换为：

（3）

其中，                           表示系统未知动态，                。

2.2 MPI模型

对于输入u，定义函数                      如下：

（u，w）=max（γp（u）-r，min（γd（u）+r，w））     （4）

其中，γp、γd：              为严格递增的连续包络函数，r为阈值，w可为任意值。则MPI模型为：

（5）

其中，    [u]（t）定义为：

[u]（0） =     （u（0），0）                                   （6）

[u]（t）=     （u（t），    [u]（tτ））

for tτ﹤t﹤tτ+1 and 0≤τ≤N-1

由于积分形式在实际应用中不易实现，可被转化为叠加形式：

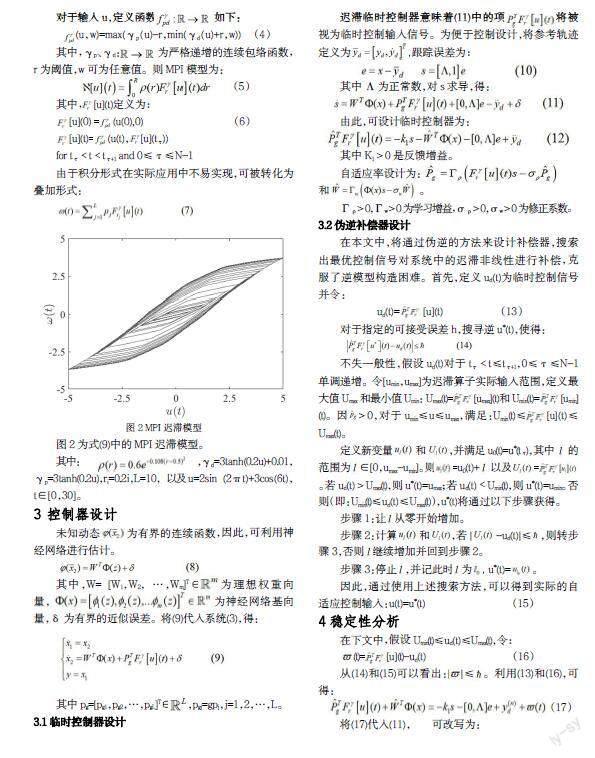
图2为式（9）中的MPI迟滞模型。

其中：                                             ，γd=3tanh（0.2u）+0.01，γp=3tanh（0.2u），ri=0.2i，L=10，以及 u=2sin（2πt）+3cos（6t），t∈[0，30]。

3 控制器設计

未知动态          为有界的连续函数，因此，可利用神经网络进行估计。

其中，W=[W1，W2，…，Wm]T∈       为理想权重向量，                                                              为神经网络基向量，δ为有界的近似误差。将（9）代入系统（3），得：

其中pg=[pg1，pg2，…，pgL]T∈      ，pgj=gpj，j=1，2，…，L。

3.1临时控制器设计

迟滞临时控制器意味着（11）中的项                   将被视为临时控制输入信号。为便于控制设计，将参考轨迹定义为                     ，跟踪误差为：

其中Λ为正常数，对s求导，得：

由此，可设计临时控制器为：

其中K1＞0是反馈增益。

自适应率设计为：

和                                  。

Γρ＞0，Γw＞0为学习增益，σρ＞0，σw＞0为修正系数。

3.2伪逆补偿器设计

在本文中，将通过伪逆的方法来设计补偿器，搜索出最优控制信号对系统中的迟滞非线性进行补偿，克服了逆模型构造困难。首先，定义ud（t）为临时控制信号并令：

ud（t）=         [u]（t）                      （13）

对于指定的可接受误差h，搜寻逆u*（t），使得：

不失一般性，假设ud（t）对于tτ﹤t≤tτ+1，0≤τ≤N-1单调递增。令[umin，umax]为迟滞算子实际输入范围，定义最大值Umax和最小值Umin： Umax（t）=        [umax]（t）和Umin（t）=        [umin]（t）。因   ＞0，对于umin≤u≤umax，满足：Umin（t）≤       [u]（t）≤Umax（t）。

定义新变量         和         ，并满足u0（t）=u*（tτ），其中     的范围为   ∈[0，umax-umin]。则      =u0（t）+    以及        =               。若ud（t）＞Umax（t），则u*（t）=umax；若ud（t）﹤Umin（t），则u*（t）=umin。否则（即：Umin（t）≤ud（t）≤Umax（t）），u*（t）将通过以下步骤获得。

步骤1：让   从零开始增加。

步骤2：计算        和        ，若|         -ud（t）|≤   ，则转步骤3，否则   继续增加并回到步骤2。

步骤3：停止   ，并记此时   为   ， u*（t）=        。

因此，通过使用上述搜索方法，可以得到实际的自适应控制输入：u（t）=u*（t）                                 （15）

4稳定性分析

在下文中，假设Umin（t）≤ud（t）≤Umax（t），令：

（t）=        [u]（t）-ud（t）                                 （16）

从（14）和（15）可以看出：|    |≤   。利用（13）和（16），可得：

（17）

将（17）代入（11），        可改写为：

（18）

其中                                                                        表示集总残差，满足                         為正常数。

定理1：对于系统（1），考虑自适应伪逆控制，若Umin（t）≤ud（t）≤Umax（t）则：s以及e收敛到零附近紧集。

证明  选择 Lyapunov函数为：

（19）

对V求导，得：                                                               。利用杨氏不等式，则：

（20）

其中：

当k1＞1/2，α和β均为正常数。据Lyapunov定理可知，V是一致最终有界，故s、e、    及    均有界。

5 仿真研究

考虑压电陶瓷微定位系统中，         =-x1-x2表示未知有界连续函数，g=1/m=1为未知参数。参考轨迹为：yd=1.2sin（t）+cos（0.5t）。为了说明本方法的有效性，将其与无伪逆补偿和PID进行了比较。设计参数为k1=8，Λ=3，Γw=Γρ=6，σw=σρ=0.5，[umin，umax]=[-15，15]。  =0.005。初始值x（0）=[0，2]T。选用RBF神经网络，m=10。对于PID，Kp=6，Ki=5，以及Kd=1。

图3和4为跟踪性能和误差的对比图，结果表明：提出的控制方法具有最佳的跟踪性能和最小的跟踪误差，从而验证了所提出的控制方案的有效性。

6 结论

本文以压电陶瓷驱动微定位平台为研究对象，构建MPI模型，利用RBF神经网络逼近系统未知动态，提出一种自适应伪逆控制方法。该伪逆控制方法是一种在线搜索机制，避免了直接构建复杂迟滞逆模型，将提出的控制方法与无伪逆补偿以及PID进行比较，表明本方法能有效地对迟滞进行补偿，能获得更好的跟踪控制效果。

参考文献

[1]许兆山.基于智能材料驱动器的非线性系统鲁棒自适应控制算法研究[D].东北电力大学，2018.

[2]王舟，陈远晟，王浩，黄勤斌.压电陶瓷驱动器迟滞建模与自适应控制[J].压电与声光，2020，42（04）：523-528.

[3]杨辉，刘俊辉，谭畅.高速列车自适应制动控制[J].计算机仿真，2021，38（11）：138-142.