不同级配结构下红层泥岩填料渗透性试验研究

白慧林

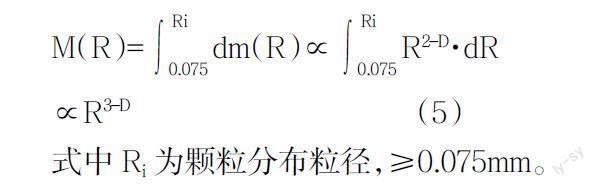
摘 要：本文以川南某国道填方工程为对象，采用不同级配梯度对红层泥岩填料进行渗透试验，并基于分形理论对级配结构与渗透性的关系进行研究。结果表明：经击实作用后，泥岩填料级配结构变好，分形维数发生增长，最大增长量可达0.24，其结构维数可作为级配量化指标。在相同级配结构下渗透系数数量级一致，渗透系数与分形维数构成多项式函数关系，实际填方工程中可采用D-k模型对整个填方工程区填料渗透系数进行计算，在减小试验工作量的同时，可对填方区大面积渗透性评价，对填方工程具有指导价值。

关键词：红层泥岩填料；渗透试验；级配结构；分形维度

1 前言

四川盆地广泛发育红层地层，形成于三叠纪～古近纪的多个地质时期，以红棕色或红褐色砂岩、泥岩、粉砂岩为主，较高的黏土矿物含量、水敏性、崩解性等是红层地层呈现出的共性，相关路基规范将红层填料划为C类填料[1-2]。近些年，西部工程建设范围不断扩大，工程建设中红层地层出现频率逐渐提高，红层砂泥岩等在工程中的利用率提升，大量学者从不同角度对红层填料展开研究，多集中于力学性质、变形等方面。徐彩凤[3]采用室内渗透试验、模型试验得出路基红层填料渗透系数随压实度增大而减小，且k水平/k垂直=1～4，各向异性显著； Dan H.C[4]针对公路排水层混合填料进行常水头渗透试验，并通过雷诺数分析发现，即便在低水力梯度下该材料渗流过程仍不服从达西定律，Forchheimer方程可代表颗粒大小、孔隙率特征。胡云鹏等[5]通过室内击实试验对红层泥岩破碎分形进行初步研究，查明P5含量变化对破碎分形的影响。

本文在前人研究基础上，以川南某国道填方工程为对象，基于破碎分形理论对红层泥岩填料渗透性展开研究，研究成果对于红层区公路填方工程建设具有指导作用。

2研究方案

2.1红层泥岩基本特征

工程区红层泥岩为侏罗系中统上沙溪庙组（J2ss），呈紫红色、红棕色，以薄层～中厚层状为主，天然密度2.39g/cm3，含水率8.6%。化学成分主要为SiO2、Al2O3，其中SiO2占比66%～74%，Al2O3占比11%～17%；其次为Fe2O3、CaO、MgO，Fe3+致使泥岩呈红色，钙、镁化合物以结核形式嵌布其中。

2.2渗透试验不同级配方案

根据工程建设实际情况，室内渗透试验分为5个级配梯度，采用等效替代法对超大泥岩块石进行处理，设计两组试验，对照组与试验组具有相同的级配。试验中定义大于5mm为粗粒，小于5mm为细粒，按粗细比分为5个梯度。

按上述级配方案配置渗透试验材料，采用室内变水头渗透试验，试样尺寸為高60cm，直径30cm，试验分多级加载水头，直至试样发生破坏。每级加载水头可精确至1cm，并采用电子秤计量单位流量，电子秤最大量程1000g，精度0.01g。

3颗粒破碎分形特征

从实际填料结构来看，整体与局部的结构、功能又呈现出自相似性，采用分形理论可对这类粗细粒混合体的自相似性进行定量分析。

根据分形理论可知，泥岩填料中颗粒直径小于R的数量N（R）与颗粒粒径R构成正相关关系，即：

N（R）∝R-D           （1）

其中，D为分形维数。

在上式基础上进行如下变换：

①对N（R）∝R-D两端进行求导：

dN（R）∝R-D-1dR                      （2）

②根据球体假设理论，小于某粒径颗粒组的总质量dm（R）与粒径R3、颗粒总数dN（R）的乘积成正比，即：

dm（R）∝R3·dN（R）                （3）

③联立（2）（3）式得：

dm（R）∝R2-D·dR                    （4）

④在式（4）基础上进行两端同时积分，则小于某粒径尺寸的泥岩颗粒质量M（R）：

M（R）=■dm（R）∝■R2-D·dR

∝R3-D                                      （5）

式中Ri为颗粒分布粒径，≥0.075mm。

⑤根据质量累计百分比P（R）与M（R）之间的正相关关系，则可知式（5）等价于：P（R）∝R3-D，在对两侧取对数后可得：

lg[P（R）]∝（3-D）lg（R）             （6）

根据式（6）中的正相关关系，以lg[P（R）]为纵坐标，lg（R）为横坐标，可建立关系曲，拟合线性其斜率n，则分形维数可表示为：D=3-n。

通过上述模型可以得到lg[P（R）]- lg（R） 曲线，进而计算出分形维度。击实前，填料分形维数介于2.34～2.59，随粗粒含量增加分维数增大；击实后，分形维数分别为2.47、2.58、2.51、2.53、2.46，介于2.46～2.58，分布区间缩减，整体维数值增大，最大变幅可达0.24。

4泥岩填料渗透性分析

4.1渗流压力对渗透性的影响

由于泥岩中黏土矿物含量较高，击实后填料结构密实，孔隙比较小，只有当水力梯度超过临界水力梯度时才能发生渗透作用。

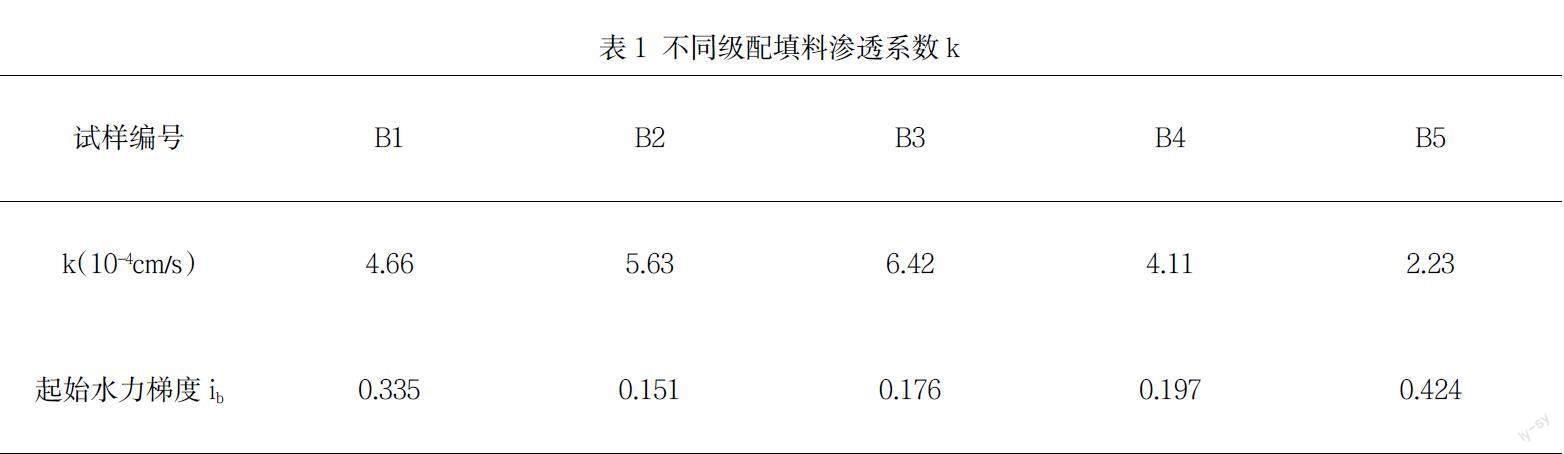
根据达西定律，起始水力梯度、渗透系数计算结果见表1。

可以看出，5个试样渗透系数具有相同的数量级，即10-4cm/s，而试样的临界水力梯度（ib）处于0.176～0.424之间，但渗透系数数值上存在一定的差异，B2、B3试样渗透系数明显高于其余三个，而临界水力梯度则正好相反。由此可见，不同级配填料击实后试样孔隙结构相近，但不同结构条件下孔隙连通特征存在差异，最终表现出不同的渗流结果。

4.2级配结构对渗透性的影响

对于填方工程而言，由于不同工程区初始级配存在差异，进而促使击实后颗粒破碎情况不同，又导致填料颗粒间孔隙大小不一致、形态多样化以及分布不均匀。根据前述分析得知，这种差异采用常规的级配结构参数来描述其级配特征已经不再适用，而分形理论基础下的分形维数介于2.46～2.58，可对试样级配结构的差异进一步细化，达到精细化评价的作用。

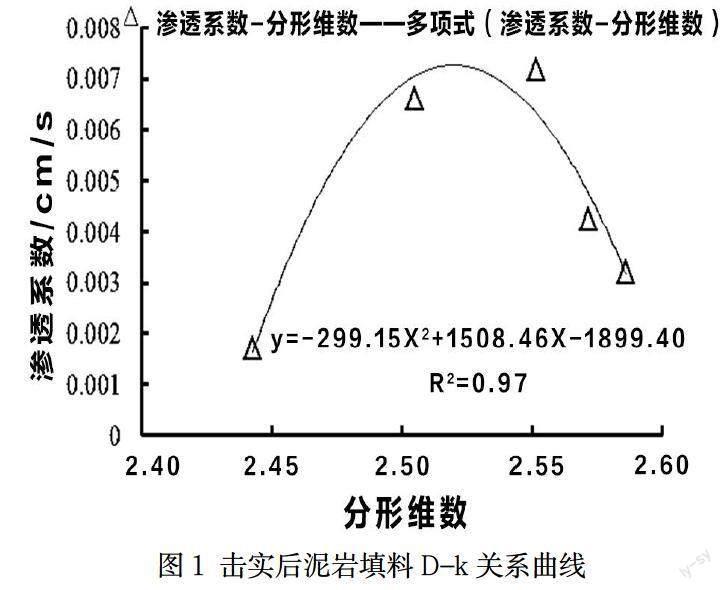
试验结果显示：相同密度、含水率的试样在前期层流状态下的渗透系数表现出等数量级，而具有同量级下的数值差异。同等数量级的渗透系数表明各试样整体渗流结构具有相似性，数值的不同以及试验后期发展走势的变化则源于试样内部孔隙组合结构的差异，通过分形理论描述试样级配结构的细微差异，建立如图1所示的曲线关系。从图中可以看出，两者之间可以拟合建立多

项式函数关系，拟合系数R2=0.97，拟合效果理想。在既定的维度区间内，渗透系数与分形维数不构成单调函数趋势，而是先增大，后减小，渗透系数存在峰值点，该峰值点对应维数的试样具有易发生渗流变形破坏的级配结构，这种级配结构是基于一定渗流条件下的相对分析结果，与通常所说的易发生渗流破坏的不良级配有所区别。

每一个填方工程所采用的回填标准可能不尽相同，进而导致最终的维度区间不一致，故D-k函数系数随波动性。针对具体的工程点，取样进行分形计算，并在相同点位完成渗透试验（5个点位以上），可建立适用于具体填方工程的D-k关系式，再对整个工程区渗透系数进行计算。对处于峰值点及其相近邻域内的点在后期出现渗流变形破坏的可能性则较大，由此可在前期进行针对性的加固处理，避免工程运营中出现渗流破坏而造成巨大损失。

5结论

（1）试样击实前分形维数处于2.34～2.59之间，较为离散，击实后分形维数介于2.46～2.58，分形维度离散化减弱，可作为评价级配特征的量化指标。

（2）经击实作用后，不同级配结构具有相似的孔隙比，其渗透系数为相同数量级，即10-4cm/s；临界水力梯度介于0.176～0.424。

（3）在既定维数区间内，分形维数与渗透系数两者之间构成多项式函数关系，实际填方工程中，可采用上述方法建立填料D-k模型，对整个填方工程区填料渗透系数进行计算。该方法在减小试验工作量的同时，可对填方区大面积渗透性评价。

参考文献

[1]王运生，吴俊峰，魏鹏等.四川盆地红层水岩作用岩石弱化时效性研究[J].岩石力学与工程学报，2009，28（S1）：3102-3108.

[2]刘长武，陆士良.泥岩遇水崩解软化机理的研究[J]. 岩土力学，2000，21（01）：28-31.

[3]徐彩風.红层填料渗透特性及渗流作用下路堤稳定性研究[D]. 西南交通大学，2007.

[4]Dan H.C， He L.H， Xu B. Experimental Investigation on Non-Darcian Flow in Unbound Graded Aggregate Material of Highway Pavement. Transport in Porous Media. 2016，112（1）：189-206.

[5]胡云鹏，冯文凯，谢吉尊等.川中红层泥岩颗粒破碎分形特性[J].长江科学院院报，2017，34（03）：115-118+125.