基于相似性的密度峰值聚类分析算法*

刘 昱 胡立华

（太原科技大学计算机科学与技术学院 太原 030024）

1 引言

聚类作为一种无监督分析方法，是机器学习和数据挖掘等领域中的重要研究内容之一［1］。聚类分析将数据对象归结为一系列聚类簇，使同簇中数据对象之间相似性较高，而在不同簇中的数据对象之间相似性较低，聚类簇有效地体现了研究对象的分布特征和潜在共性，对于揭示事物的内在联系具有重要意义，并已广泛地应用于社会科学［2］、并行计算［3］、信息检索［4］、机器学习［5］和数据挖掘［6］等领域。

DPC［7］是具有代表性的一类密度聚类分析方法，但由于对数据集的大小和密度的度量未明确定义，参数截断距离dc选择上存在很大随意性，且在找到密度峰后，仅将剩余数据对象分配给距离最近的较高密度点容易导致误传播，从而导致复杂数据集的聚类性能较差。本文利用数据对象的K 近邻得到局部密度，再通过与其K近邻数据对象局部密度和距离的比值得到邻域密度，重新定义了局部密度计算方法，有效地解决了截断距离dc在选择上的随意性；其次针对数据对象之间的相似性，结合影响空间、共享K近邻和密度比提出了一种新的数据对象相似性度量方法；根据K近邻距离的内聚性系数先标记低内聚性点，再依据距离和密度相似性并结合相似近邻思想进行聚类，改进了FKNN-DPC分配策略。

2 相关工作

近年来，其典型研究工作：Alex 等首先提出快速搜索和查找密度峰（DPC）聚类分析思想和方法；Mehmood 等提出利用基因表达微阵列和密度峰值结合算法［8］，有效为癌症分型和肿瘤组织识别；Liu等提出共享最近邻的密度峰快速搜索聚类算法［9］，根据共享邻域计算点之间的相似度，并通过相似度重新定义点的局部密度，并提出自适应距离度量方法，但是聚类算法受共享邻居数影响较大；Xie等提出根据K近邻的密度峰值聚类算法FKNN-DPC［10］；Xu 等提出了基于累积最近邻度和微观聚类合并的密度峰聚类算法［11］，重新定义局部密度，并且引入合并微集群方法提高分配精度；Du 等提出基于K近邻和主成分分析的密度峰聚类算法［12］，利用PCA降维有效改进DPC 在高维数据集中聚类效果较差的缺点，虽然提高性能，但是聚类效果受数据对象的分布影响较大；高鑫等提出将Word2Vec 与密度峰结合的算法［13］，通过KNN 改进数据点的局部密度计算公式并通过最小二乘法选取聚类中心，有效提高搜狐新闻数据集的聚类结果。

3 DPC聚类

对于给定任意数据集X={x1,x2,…,xn} ，dij表示数据对象xi和xj之间的欧式距离，dc是由用户设置的截断距离，则局部密度ρi定义为

δi是数据对象xi与较高密度数据对象xj之间的最小距离，距离定义为

如果数据对象xi具有全局最高密度，则公式定义为

为了检测数据集中的聚类簇数，DPC提出启发式方法（决策图），决策值γi的定义为

由上述公式，然后DPC算法将剩余的未分配的数据对象分配给距离最近的较高密度点所属的簇。

4 基于相似性的密度峰值聚类分析

4.1 基本思想

本密度计算方法将数据对象密度分为两部分：1）FKNN-DPC［10］的数据对象的K 近邻局部密度；2）数据对象局部密度与其K 近邻局部密度和距离的比值得到的邻域密度，可有效解决人为设置截断距离dc的问题；针对数据对象之间的相似性，结合影响空间、共享K近邻和密度比提出一种新的数据对象相似性度量方法，依据距离和密度相似并结合近邻思想，充分考虑扩展点与最相似的被扩展点的周围邻近点的距离分布情况和两点之间的密度分布相似性，从而扩展聚类簇，改进了FKNN-DPC［10］分配策略。

对于给定任意数据集X={x1,x2,…,xn} ，xj是数据对象xi的K 近邻数据对象，dij表示数据对象xi和数据对象xj之间的欧氏距离，则数据对象xi的局部密度ρi1为

每个数据对象xi的邻域密度比定义为ρi2：

每个数据对象xi的真实密度定义为

根据式（8），通过计算每个数据对象的局部密度和邻域密度比之和，有效避免K近邻之和相同的情况，计算数据对象局部稠密情况和与其周围邻域的密度比值情况，真实反映数据对象在数据集中密度情况。

逆近邻集合由文献［14］定义，对于给定任意数据集X={x1,x2,…,xn} 中，RNNi是数据对象xi的逆近邻集合，则数据对象xi的逆近邻集合定义为

根据式（9），数据对象的逆近邻集合反应此数据对象在数据集中的被影响情况。当数据点处在高密集区域时，通常会被较多的数据对象包围，当数据对象的逆近邻对象较少时，表明此数据对象处在稀疏区域。

影响空间IS 由文献［15］定义，则数据对象xi的IS(i)定义为

根据式（10），影响空间IS反映了数据对象之间的双向邻域关系，当两个数据对象在影响空间时，表明两个数据对象的紧密程度大于单向K近邻，能够准确反映两个数据对象的相似性较高。

共享K 近邻由文献［16］定义，任意两个数据对象xi和xj的共享K近邻个数定义如下：

对于给定任意数据集X={x1,x2,…,xn} 中，数据对象xi和xj之间的相似性定义为以下六种情况：

数据对象xi和xj存在影响空间且存在共享K近邻，则数据对象xi和xj的相似性公式定义为

数据对象xi和xj存在影响空间但不存在共享K近邻，则数据对象xi和xj的相似性公式定义为

数据对象xi和xj不存在影响空间但存在共享K 近邻且xj是xi的K 近邻，则数据对象xi和xj的相似性公式定义为

数据对象xi和xj不存在影响空间且xj不是xi的K 近邻但存在共享K 近邻，则数据对象xi和xj的相似性公式定义为

数据对象xi和xj不存在影响空间且不存在共享K 近邻但xj是xi的K 近邻，则数据对象xi和xj的相似性公式定义为

数据对象xi和xj不存在影响空间且不存在共享K 近邻且xj不是xi的K 近邻，则数据对象xi和xj的相似性公式定义为

上述式（12）~（17）定义数据对象之间的相似性计算方式能够区分局部数据区域、不同簇之间的样本。当两个数据对象在影响空间，我们对在影响空间内的数据对象予以双倍距离相似性。双向近邻与单向近邻不同，单向近邻仅仅表示某个数据对象对另外一个数据对象的联系，不能反映两个数据对象是否具有紧密关系。若两个数据对象之间只存在单向近邻，表明两个数据对象分布在两个不同紧密的簇或者彼此相离较远也可能为离群点；若两个数据对象为双向近邻，表明那两个数据对象大概率分布在同簇内或者相离较近。若两个数据对象之间不存在影响空间但是有共享K近邻时，表明这两个数据对象存在共享数据对象将彼此相连，表明彼此之间具有相似性，但是相似性不高。若不存在共享K 近邻且不存在影响空间和K 近邻，表明两个数据对象之间没有相似性，这两个数据对象的相似性为0。通过将两个数据对象的密度做比值可得出，若密度值差异不大，比值趋近于1，表明两个数据对象密度相似，属于同簇中的概率较大。

数据对象xi的相似性K 近邻集合为与xi相似性最大的K个数据对象，同时将K近邻集合替换：

在相似性扩展聚类算法中，最常用的方法是基于距离的度量，将距离聚类中心点最近的数据对象归属于中心点相同的簇中，但无法考虑聚类扩展点和其周围邻近点的分布情况，导致忽略数据对象之间的密度相似性。因此在扩展聚类过程时，不仅要考虑距离相似性，同时还要考虑数据对象之间的密度分布相似性。如图1 所示，密度之差较小时，表明同簇数据对象之间分布相似，此时两个数据对象归属于相同簇的概率高。从而改进了FKNN-DPC［10］的聚类簇扩展和分配策略过程。

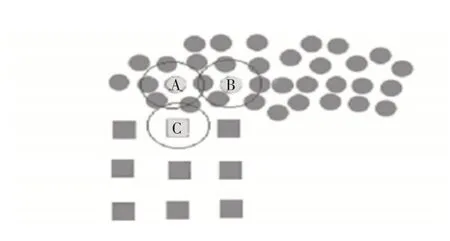
图1 密度相似示意图

对于每个未分配点xi，点xj为点xi的相似近邻且xj已经被分配，定义yj=c（c=1，2，…，m）表示为xj被分配所属类标签，wij=1/(1+dij)，γij为相似度的归一化值，|ρi-ρj|为两个数据对象之间的密度差异性，则归属度P如式（19）所示：

根据式（19），归属度P受两个影响因素：1）数据对象的SimKNN；2）两个数据对象之间的密度差异性。γij和密度差异同时决定归属度P，γij值越大，表明两个数据对象距离越近，符合距离越近簇相同；密度差异越小，表明两个数据对象之间的分布相似性越大，符合点分布相似簇相同的情况。两个值越大表明已分配数据对象xj对未分配点xi的归属度影响越大，则归属于相同簇的概率越大。

参照文献［7］，在聚类扩展过程中，如果两个簇有交集，则两个簇可能会受到交集的影响而合并为一个簇。所以根据文献［17］筛选低密度点的方法标记低内聚性点，数据对象xj的内聚性β由式（20）定义，内聚性标准值为所有点的β之和的平均值η由式（21）定义，那么低内聚性集为低于内聚性标准值的点集由式（22）定义。

4.2 算法描述与时间复杂度分析

算法S-DPC，输入：数据集X，近邻数K

输出：簇标签

1）数据预处理：归一化数据。

2）依据式（3）和式（8），计算数据集X中的每个数据对象的δ和ρ值。

3）由每个数据对象的δ和ρ乘积绘制决策图，选取决策值较高点为簇中心点，并添加至簇中心集合。

4）计算SimKNN。

5）将簇中心集合中每个未分配的数据对象j标记为已分配的簇中心，并将SimKNNj归属到数据对象j所在的簇，然后都添加至初始化后的队列Queue。

6）依据式（20）、（21）和（22）计算内聚性标准值，将内聚性值小于标准值且未分配的数据对象标记。

7）采用近邻扩展策略分配数据对象：

（1）选取Queue 中的第一个数据对象i，然后将满足相似 性 值 条 件 ：Sip≥ mean （Spk） ；其 中pϵSimKNNi、kϵSimKNNp的对象i的未被分配且高内聚性SimKNN分配至点i所属的簇，并添加至Queue队列尾部。

（2）若Queue队列不为空，则转至（1）。

8）使用学习概率策略分配数据对象：

（1）将步骤7）中未分配的n个数据对象构成n×m矩阵，存储每个未分配数据对象的，同时将矩阵每行中的最大归属度值max添加至列表ListP 中，最大归属度所属的簇类别arg max添加至ListA中。

（2）如果还有未分配点，则搜索和分配最大归属度值点i对应arg max，并转至下一步；否则退出分配算法。

（3）更新矩阵和列表，更新SimKNNi中的每个数据对象q的归属度：，更新两列表对应的max和arg max并转至（2）。

9）对于仍未被分配的低内聚性数据对象，分配其到已分配的最近所在的簇中。

对S-DPC 算法进行分析，主要由以下部分构成：计算距离为O（n2），计算共享K 近邻为O（kn2），利用Kd-tree 查找数据对象的K 近邻为O（nlog2(n)），计算与较高密度点最小距离为O（n2），计算逆近邻为O（n2），计算局部密度为O（kn），计算邻域密度比为O（kn），计算相似K近邻为O（n2），计算内聚性值为O（kn），近邻扩展策略为O（n'm），学习概率策略为O（n''2）。整体的时间复杂度近似为O（kn2）。

5 实验结果与分析

实验环境：Windows 10 64 位操作系统，i5-8300H 处理器，8GB RAM，编程环境为PyCharm。为了验证算法S-DPC 性能，采用UCI 数据集，并与相关算法DPC［7］、FKNN-DPC［10］、DBSCAN［18］、AP［19］、K-means［20］进行实验分析比较，选取6个UCI数据集，详见表1。

表1 UCI数据集

聚类评估指标：为评估S-DPC 算法聚类性能，采用聚类准确率（Acc）、调整互信息（AMI）、调整兰德系数（ARI）三个度量聚类性能指标［21］。

如图2~图4所示，S-DPC算法的聚类性能高于其他聚类算法，其主要原因是能适应性的计算数据对象密度，正确找到聚类中心点，且扩展聚类过程中充分考虑距离和密度两种影响因素，依据距离和密度相似并结合最相似近邻思想，综合扩展点与被扩展点的周围邻近点的距离分布情况和两点之间的密度分布相似性扩展聚类簇，改进了FKNNDPC［10］的聚类簇扩展和分配策略过程，有效地提高聚类性能。

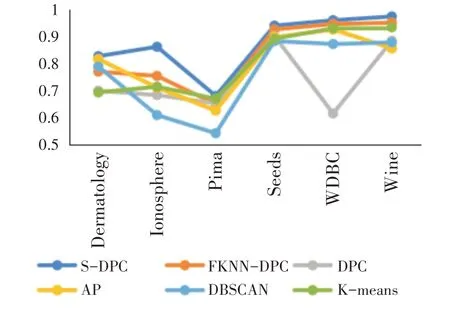
图2 聚类准确率比较

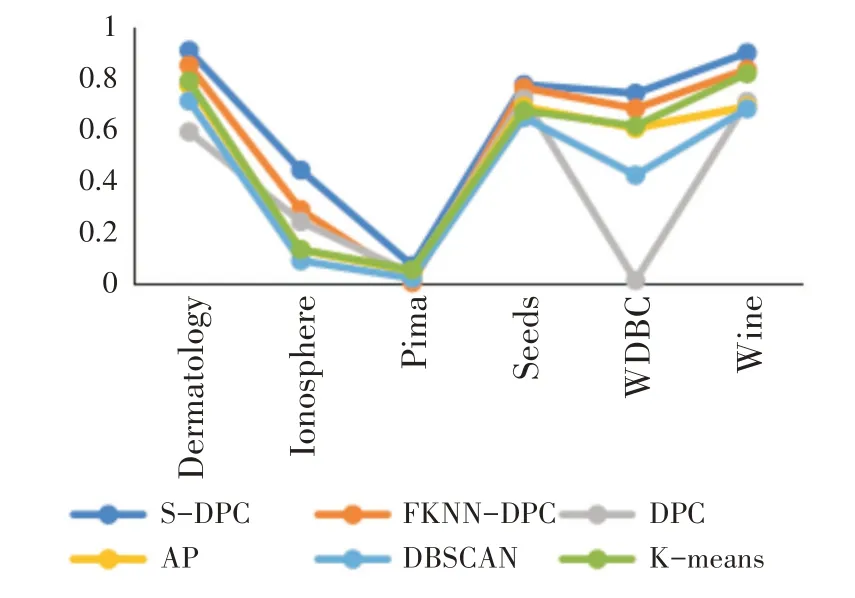
图3 调整互信息比较

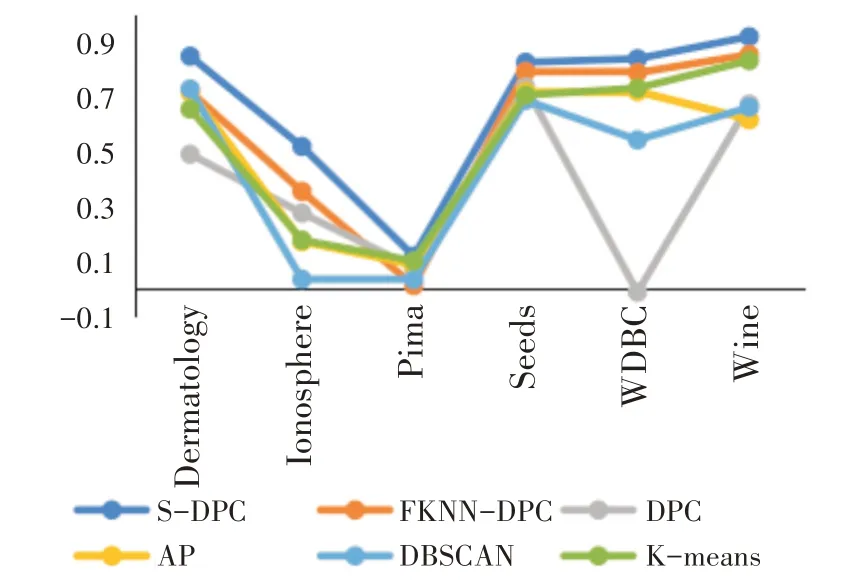
图4 调整兰德系数比较

6 结语

本文利用数据点相似思想，提出了一种密度峰值聚类分析算法S-DPC。在本文中该算法首先将密度公式分为两个部分，利用数据对象的K近邻得到局部密度，再通过与其K近邻数据对象局部密度和距离的比值得到邻域密度值；其次针对数据对象之间的相似性，结合影响空间、共享K 近邻和密度比提出了数据对象相似性度量方法；又结合数据对象的距离和密度相似的影响因素并与最相似近邻结合，给出了基于距离和密度的聚类簇扩展方法，充分考虑扩展点与最相似的被扩展点的周围情况，从而扩展聚类簇，改进了FKNN-DPC 分配策略过程，有效地提高密度聚类分析性能。