基于最小冗余动态加权的信息论特征选择算法*
2023-09-29吴自华周从华
吴自华 周从华
(江苏大学计算机科学与通信工程学院 镇江 212013)
1 引言
特征选择(Feature Selection)是在保持原始数据准确率的同时,显著降低特征空间的维数的过程。特征子集的筛选也可以看作是对特征空间的搜索。其中搜索方向和搜索起点至关重要。基于搜索方向,一般有三大搜索策略:完全搜索、顺序搜索、启发式搜索[1~2]。完全搜索实际上就是对特征集合的穷举搜索,准确率高但工作量大。顺序搜索包含序列前向搜索和序列后向搜索。序列前向搜索首先初始化特征子集S为空集,依次从原始特征集合F中筛选一个特征Xi,使得评价函数J(Xi)取最大值,将此特征Xi加入特征子集S直至达到终止条件。序列后向搜索则与此相反。应用较多的是启发式搜索,它包含我们熟知的粒子群等群智能算法。启发式搜索降低了时间复杂度,但在后期容易陷入局部最优值。
在特征选择领域中,基于互信息的特征选择算法占有重要地位。互信息是一种衡量两个随机变量相关性的方法。在已知一个变量的前提下,互信息代表根据已知变量的信息得到的另一个变量不确定性减小的程度。由于这种关联性,互信息在特征选择领域经常被用来计算特征与类别的相关性或特征与特征之间的冗余性。
本文主要做了三点工作:
1)通过一个例子,详细说明ICI[6]公式中存在的在新分类信息一致的条件下,该公式有可能偏向高冗余特征的问题。
2)针对上述问题,提出两个基于类别相关性的动态权重,通过配置权重从而间接减少冗余信息在评价函数中的占比,在不对相关性计算出现大偏差的前提下减小ICI对高冗余特征的偏向性。
3)对设置的两个动态权重进行合理性分析,验证它们在各种情况下不会对相关性计算出现大的偏差,保证算法对相关性计算的合理性。
2 相关工作
2.1 信息熵与互信息
信息熵可看作是对随机变量不确定程度的衡量,其计算方式如下:
若离散变量X共有n种取值,p(xi)代表每种取值的概率。除单个随机变量外,还有关于两个随机变量的联合熵,定义如下:
联合熵代表两随机变量X,Y同时发生的不确定程度。互信息就是基于上述两个概念计算得到,定义如下:
I(X;Y)代表已知变量X的条件下,变量Y不确定性减少的程度。互信息可用来衡量两个随机变量的相似程度。一般将特征Xi与目标类别C的互信息称作特征的相关性:
相关性越大的特征对目标类别的识别能力越强。特征Xi与特征Xj之间的互信息称为冗余性:
互信息中还对条件相关性做出了如下定义,Xi,Xj代表候选特征,C代表目标类别:
条件相关性代表特征Xi在特征Xj的条件下对类别C的相关性。
2.2 互信息特征选择算法
基于互信息的特征选择算法的任务是选出与目标类别相关性最大的特征子集,子集与类别的相关性可用如下公式表示:
求得能使I(S;C)取最大值的特征子集S 即是特征选择算法的目标。
Battiti在1994 年提出MIFS[3]算法,该算法用候选特征的相关性减去特征之间的冗余性来度量特征子集的优劣,公式如下:
针对MIFS中β参数难以确定的问题,mRMR[4]采用平均冗余度作为衡量候选特征与当前特征子集的冗余性,设,标准如下:
除了考虑单个特征对类别的相关性外,Yang等[5]提出利用联合互信息衡量候选特征对目标类别的相关性:
与以上经典的特征选择算法不同。也有不同风格的互信息特征选择算法被提出,例如Zeng[5]提出使用一种动态交互因子IW(Xi,Xj)来衡量两特征间的关系,对IW(Xi,Xj)的定义如下:
该算法依据IW(Xi,Xj)的取值范围来判定两特征究竟是冗余还是交互关系,相对传统的计算方法是较为新颖的思路。
综上所述,基于互信息的特征选择算法大多围绕着“最大相关-最小冗余”原则来设计评价函数。在提高子集对类别相关性的同时,也要注意降低子集内部的冗余性,避免因为子集内部的高冗余性而降低算法的准确率。
3 MRDW-ICI算法
3.1 ICI的偏向性问题
大多数互信息特征选择算法通常采用如下公式计算特征子集与类别的相关性,F代表待选特征的集合:
考虑到在已选特征不变的条件下,不同的候选特征与已选特征组成的集合对目标类别的相关性是会变化的。Qun Wang 等在2017 年提出了ICI[6]度量公式,公式如下:
从公式中可以看出,ICI 是两个条件相关项之和。该公式不仅考虑到了候选特征在已选特征的条件下对目标的相关性,还考虑到了已选特征在不同候选特征的条件下对目标分类信息产生的变化。
虽然ICI更加综合地考虑了特征子集的相关性计算,但它也存在着一些问题。例如在同一个已选特征分别与两个候选特征Xi与Xm组成的子集能提供的新分类信息一致的前提下,该公式偏向于与已选特征组成子集后,子集内冗余信息更高的那一个特征。为了方便说明,如图1、图2所示。
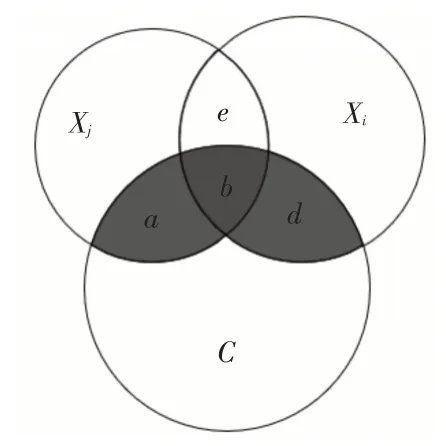
图1

图2
Xi与Xm代表候选特征,Xj代表已选特征。图1中a,d,e分别代表I(Xj;C|Xi),I(Xi;C|Xj),I(Xi;Xj|C)。图2 中f,h,i分别代表I(Xj;C|Xm),I(Xm;C|Xj),I(Xm;Xj|C)。为方便表示,本采用文献[8]中的概念,分别用I(Xi;Xj;C)表示b区域,I(Xm;Xj;C)表示g区域。
若a+d=f+h,这说明候选特征Xi,Xm各自与已选特征Xj组成的集合对目标类别的相关性是一致的。即有:
但通过观察图1中的b区域和图2中的g区域,可以发现明显有g>b,即有I(Xm;Xj;C)> I(Xi;Xj;C)。在H(Xm)>H(Xi)时可知这种情况是存在的。由于ICI(Xi)= ICI(Xm)且I(Xm;Xj;C)>I(Xi;Xj;C),说明Xj与Xm组成的子集和Xj与Xi组成的子集在分类能力一致的前提下,前两个特征组成的冗余信息大于后两个特征组成的冗余信息。因此基于“最大相关-最小冗余”原则,Xi应该优于Xm。但在ICI 的标准下,Xi与Xm的评价值却是相同的。换句话说,在新分类能力[6]相同时,存在ICI 会更偏向于高冗余特征的问题。
3.2 算法原理
上一节明确了ICI公式在已选特征不变的条件下,子集新分类能力一致时会偏向高冗余特征这一问题。本节引入两个基于特征相关性的动态权重,通过间接求解最小冗余的方式来降低特征子集的冗余度,从而改善ICI对高冗余特征的偏向性。
由于Xi是待选特征,故I(Xi;C)的值是动态变化的。而Xj是已选特征,故可将I(Xj;C)看做是一个常数。由信息论推导可得:
为方便表示,这里用IC(Xi;Xj)代表I(Xi;Xj)-I(Xi;Xj|C)。即有:
不难发现在I(Xj;C)是常数的前提下,I(Xj;C|Xi)的大小和IC(Xi;Xj)成反比。即当I(Xj;C|Xi)增大的时候,IC(Xi;Xj)减小。当I(Xj;C|Xi)减小的时候,IC(Xi;Xj)增大。所以可将最小化冗余信息IC(Xi;Xj)的求解等价转换为最大化I(Xj;C|Xi)的求解。
因此对于I(Xi;C|Xj)+I(Xj;C|Xi),可将左项I(Xi;C|Xj)看作衡量Xi的新分类信息的项式。将右项I(Xj;C|Xi)看成衡量Xi与已选特征Xj冗余性的项式。I(Xi;C|Xj)越高,代表Xi与类别C的独立相关性[6]越强。在已选特征不变的条件下,针对不同的候选特征Xi,若I(Xj;C|Xi)越高,既代表Xj的新分类能力越高也代表Xi与Xj的冗余信息越低。
为了使评价函数在新分类能力一致时更偏向低冗余特征,不妨提高I(Xj;C|Xi)在评价函数中的占比。基于此思路,本文提出MRDW-ICI(Minimal Redundancy Dynamic Weight-ICI)算法,算法公式如下:
不难发现,式(18)实际上是对ICI 公式的左右两项分别加了两个动态权重ω1和ω2。由信息论可知,0 ≤I(Xj;C)≤H(C),0 ≤I(Xi,Xj;C)≤H(C),所以有0 ≤ω1≤1,0 ≤ω2≤1。又因为I(Xi;C)≤I(Xi,Xj;C),所以有ω1≤ω2。 综上可得,0 ≤ω1≤ω2≤1。
因为ω1≤ω2,所以当I(Xj;C|Xi)=I(Xi;C|Xj)时,I(Xj;C|Xi)在整个评价函数中的占比提高了,也就达到了评价函数在子集新分类能力一致时,偏向低冗余特征的目的。
3.3 权重合理性分析
虽然MRDW-ICI 算法实现了在子集新分类能力一致时,让评价函数偏向低冗余特征这一目的。但若权重ω1,ω2设置不合理,例如无限放大低冗余项在评价函数中的占比,那么反而会造成算法对子集相关性的计算失误。本节基于候选特征与已选特征的关系对两权重的合理性进行分析,若计算结果与ICI 差距不大,则证明没有因为添加动态权重的原因而导致对子集相关性的计算出现较大偏差。设Xi,Xm为候选特征,Xj为已选特征,,分析如下:
两候选特征都与已选特征存在冗余:
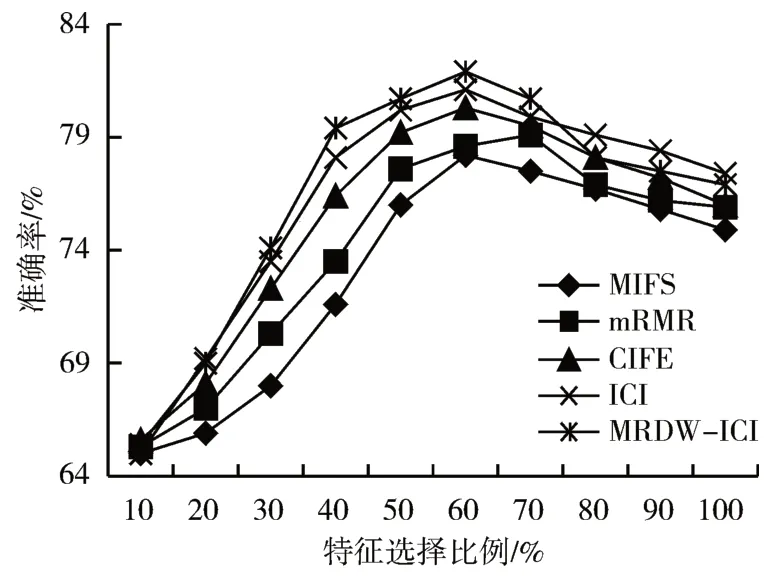
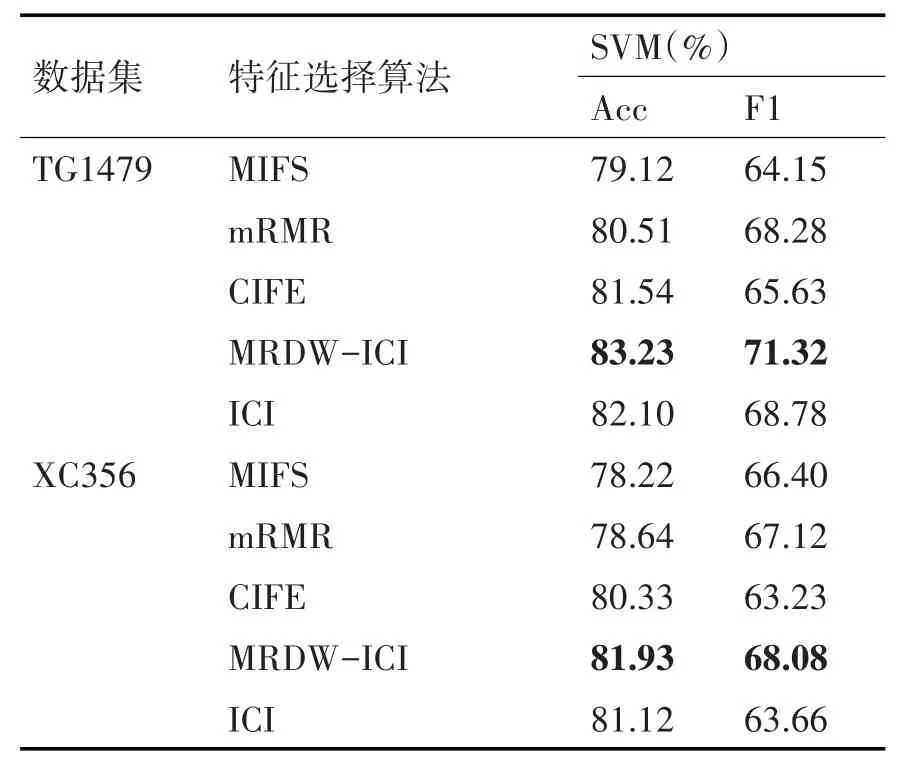
1)若I(Xi;C|X)j=I(Xm;C|X)j,当(IXj;C|X)i>(IXj;C|Xm)时,因为ω1=,且有I(Xi,Xj;C)> I(Xm,Xj;C),故ω2>,于是J(X)i>J(Xm),结果和ICI 一致。反之当I(Xj;C|X)i 两候选特征都与已选特征互相独立: 此时I(Xi;C|Xj)=I(Xi;C),I(Xj;C|Xi)=I(Xj;C)。于是式(19)可化简为如下形式: 因I(Xj;C)为常数,不难发现式(20)实际是一个关于I(Xi;C)的线性函数,因此J(Xi)随I(Xi;C)单调递增。当I(Xi)>I(Xm)时,有J(Xi)>J(Xm),与ICI结论一致。 其余情况下,MRDW-ICI 算法较之ICI 会更偏向低冗余特征。 但由于0 ≤ω1≤ω2≤1 ,故0 ≤ω2-ω1<1 。因此算法对低冗余的偏向值(ω2-ω1) ×I(Xj;C|X)i小于I(Xj;C|X)i本身,且实际来说ω2-ω1的值通常较小,因此该偏向值并不会被无限放大,处在合理可控的范围内。 算法详细流程如下: MRDW-ICI算法步骤: 输入:数据集D={x1,x2,…,xm} 、最优特征子集数目k、目标类别C、待选特征集合F 硬件配置:CPU:Intel(R)Core(TM)i5-8250U(1.60GHz~1.80GHz) ,GPU: NVIDIA GeForce MX150,内存8GB,硬盘256G。软件配置:Windows10操作系统(64位),Python3.7.0版本。 实验所用原始数据来自无锡市儿童医院的血常规指标,共有两份数据集。分别是体检数据集TG1479 和哮喘数据集XC356。两份数据集均对哮喘的轻症与重症做了标注,即样本类别已经标注完毕。详见表1。 表1 数据集描述 本文使用分类实验常用的评价指标,即预测的准确率(Accuracy)及F1值对分类结果进行评价,分类结果的“混淆矩阵”如表2所示。 表2 混淆矩阵 F1 值是由查准率和查全率确定的,这三者的公式根据上表分类结果有如下定义: 本文数据集内的数据皆是连续值,对于连续值,在计算互信息的时候需要知晓每个特征对应的函数分布,为了简化互信息的计算,本文采用数据离散化的方法将连续数据转变为离散数据,方便后续的计算。 鉴于本文数据集内同一特征下数据取值范围较广,为了计算简便,本文采用传统的5 箱等宽法将同一特征划分为5 个不同的取值,从而完成数据的离散化工作。 为评估MRDW-ICI算法的筛选效果,本实验采用经典的特征选择算法MIFS,mRMR,CIFE 及ICI与其进行对比。MIFS 中的β取1。选择MIFS,mRMR,CIFE这三种算法是因为这三种算法既是公认的较为经典的互信息特征选择算法,同时这三种算法也都对特征子集内的冗余性做了考虑。较之以只考虑候选特征对目标类别相关性的算法,明显前面三者要更为优秀。 实验选用在二分类问题上有较好表现的SVM分类器,分别评估以上五种特征选择算法筛选出的特征子集的分类效果。在相同特征数目的前提下,准确率越高,说明该特征子集对目标类别的相关性越强。 为降低数据集因为分为训练集和验证集带来的随机性影响,本实验采用十折交叉验证法。通过对比相同特征数目下的准确率以及对比各个特征选择算法筛选出的特征子集的最高准确率来验证本文提出的算法的有效性。实验结果如下,图3 和图4是两数据集TG1470与XC356在SVM 分类器下的准确率对比。 图3 TG1470数据集上的SVM分类准确率 图4 XC356数据集上的SVM分类准确率 分析上面两图可知,特征子集在特征数目递增的情况下,其与类别的相关性大体呈现出先增大后减小这样的一种趋势。子集的选取比例在10%的时候准确率最低。在图3 中MIFS 在比例达到70%的情况下准确率达到最高值79.5%,剩余的四个算法均在60%的比例下即可达到最高值。其中MRDW-ICI 算法的准确率最高达到83%。在达到最高值后,除MIFS 外,剩余4 种算法的准确率均在选取比例超过60%后呈现不同的下降趋势。且图3中特征选取比例在大于70%后,ICI 的准确率再度逐渐超过本算法。 分析图3 发现,在特征选取比例在10%的条件下,ICI的准确率高于MRDW-ICI,这说明此时子集内高相关特征的收益大于低冗余特征带来的收益。 在选取比例为30% ~70% 的条件下,MRDW-ICI 的准确率均在ICI 之上,这说明在剔除子集内的冗余信息后,子集对目标类别的相关性获得了显著增长。 表3 是数据集在SVM 分类器下的最高准确率和F1值。 表3 5种特征选择算法的准确率及F1值 由上表可知,MRDW-ICI算法对比其余四种算法均能取得不错的分类效果。其在TG1439数据集和XC356 数据集的最高分类准确率分别是83.23%,81.93%。不仅准确率有所提升,且其在对应的F1 值上分别提高2.54%和4.42%。这说明MRDW-ICI算法筛选出来的特征子集较ICI不仅相关性上升,且具有更强的稳定性。 本文针对ICI公式在新分类能力一致时可能会偏向高冗余特征的问题进行改进。通过引入两个基于相关性的动态权重,从而间接减少类内冗余信息在评价函数中的占比,降低ICI 公式在新分类信息相等时对高冗余特征的偏向性,并将其应用到筛选最优特征子集中。下一步的工作是考虑如何基于数据的分布特点提高分类器的精度,使得特征子集的分类效果能进一步提升。
4 实验
4.1 实验环境及配置

4.2 实验评价指标

4.3 数据预处理
4.4 实验结果分析

5 结语
