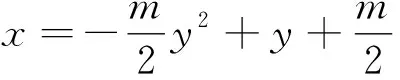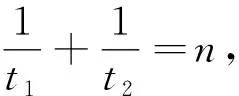“双根”技巧简化运算,等价转化探究本质

广东省佛山市顺德区容山中学 (528303) 黄桃荣

解决轨迹问题的一般方法是设点,通过题干发现点所满足的关系式,化简关系式求得结论.当题干条件复杂时,如何选择切入点则是解决此类问题的关键.笔者研究了2023届广州市高三调研测试第21题,通过该题的解答过程,很好地体现了如何设点以及消元的完整过程,现将笔者的思考展现如下,以飨读者.

一、题目

已知抛物线C:y2=2px(p>0)的焦点到准线的距离为2,圆M与y轴相切,且圆心M与抛物线C的焦点重合.(1)求抛物线C和圆M的方程;(2)设P(x0,y0)(x0≠2)为圆M外一点,过点P作圆M的两条切线,分别交抛物线C于两个不同的交点A(x1,y1)、B(x2,y2)和Q(x3,y3)、R(x4,y4),且y1y2y3y4=16.求证:点P在一条定曲线上.

分析：本题的主题干对抛物线与圆的信息交代的非常清晰,且考查的方式也很直接,抛物线C的方程为y2=4x,圆M的方程为(x-1)2+y2=1,过程略.本题的难点主要集中在第(2)问,涉及到了圆的切线,直线与抛物线相交,四个交点的纵坐标满足某种关系式.并证明点P在一条定曲线上.考查的因素很多,且条件环环相扣,但所求的是一条轨迹问题.但题干没有直接计算点P的轨迹(通过后文可知其轨迹为圆的一部分),该设问方式反而降低了要求(回避了分析在所求的轨迹中排除不满足的部分).

二、解法呈现

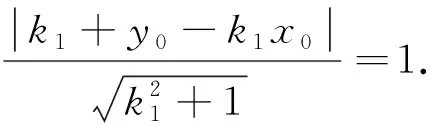
综上即可知点P在定曲线x2+y2=1上运动.

评注：上述解法即是按照题干条件出现的顺序,逐渐深入完成求解.思维过程简单,但涉及到的运算量较大.但在本文中多次出现了“整体代换”的技巧,例如本文研究了k1的表达式后通过类比即可得k2的表达式,从y1y2到y3y4也是运用的该思想.

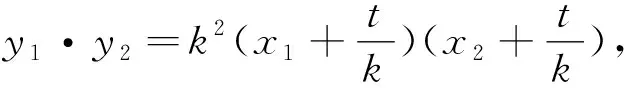
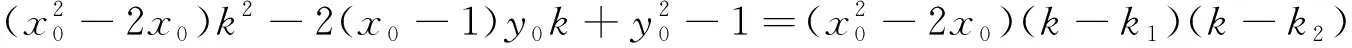
提示：若以m1,m2为变量,可直接设直线AB的方程为x=m1(y-y0)+x0进行运算.

三、背景探究及模型推广

根据上面的解答过程可知,解题的核心在于对y1y2y3y4=16的解析,为了有效地说明该结论对应的本质.我们先看如下的一个引理.

引理设点P(t,0),过点P作直线l与抛物线C:y2=2px交于A(x1,y1)、B(x2,y2)两点,则y1y2=-2pt.

证明:设直线l:x=my+t与抛物线的方程y2=2px联立可得y2-2pmy-2pt=0.根据韦达定理可得y1y2=-2pt.

在原问题中,设直线AB,QR与x轴交点的横坐标分别为t1,t2.根据引理可得y1y2=-4t1,y3y4=-4t2,即等价于t1·t2=1.那么原问题可进行如下的改述:设P(x0,y0)(x0≠2)为圆M:(x-1)2+y2=1外一点,过点P作圆M的两条切线,设两条切线与x轴交点的横坐标分别为t1,t2,若t1·t2=1,求证:点P在一条定曲线上.

该转述完全回避了抛物线的作用,回到了问题的本质.接下来,本文将尝试直接转述后的问题.

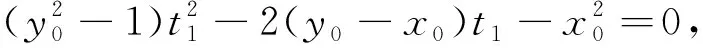
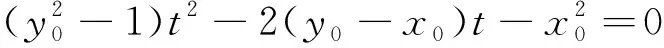
通过上述解答过程,可快速将上述模型进行推广.例如我们可以得到如下的结论:

结论1 设P(x0,y0)(x0≠2)为圆M:(x-1)2+y2=1外一点,过点P作圆M的两条切线,设两条切线与x轴交点的横坐标分别为t1,t2,若t1·t2=s(s>0),则点P在x2+sy2=s上运动(即其轨迹为椭圆).