谨防隐含条件的陷阱

文／周华军

一、忽视等式性质的使用条件

例1方程x2=x的解是________。

【错解】两边同除以x，得x=1。所以方程的解是x=1。

【剖析】等式性质2 是：等式两边同时乘同一个数（或除以一个不为0 的数），所得结果仍是等式。错解中两边同除以x，忽视了x可能为0 的情况，导致漏解。

【正解】移项，得x2-x=0。所以x（x-1）=0。所以x1=0，x2=1。

【对策】方程的根是使方程成立的未知数的值，不管遇到多么简单的方程，一定要按照解方程的步骤去求解。

二、忽视一元二次方程的概念

例2已知关于x的一元二次方程kx2-（2k+4）x+k-6=0 有两个不相等的实数根。求k的取值范围。

【错解】因为关于x的一元二次方程kx2-（2k+4）x+k-6=0 有两个不相等的实数根，所以根的判别式b2-4ac=（2k+4）2-4k（k-6）＞0，解得

【剖析】一元二次方程的二次项系数不为0，这一点在解题过程中经常被同学们忽视，导致答案错误。

【正解】因为关于x的一元二次方程kx2-（2k+4）x+k-6=0 有两个不相等的实数根，所以k≠0 且根的判别式b2-4ac=（2k+4）2-4k（k-6）＞0。解 得且k≠0。

【对策】理解一元二次方程的概念是解决此类问题的起点。解决一元二次方程的相关问题时，一定要抓住“二次”，只有二次项系数不为0，才能保证“二次”的存在。

三、忽视实际问题的背景

例3某学校计划利用一片空地为学生建一个面积为80m2的矩形车棚，其中一面靠墙（墙的可用长度为12m），已知现有的木板材料可使新建板墙的总长为26m。根据学校要求，在与墙平行的一面开一个2m 宽的门（如图1），那么这个矩形车棚相邻两边长分别为多少？

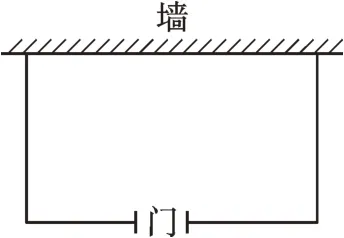
图1

【错解】设与墙垂直的边长为xm，则与墙平行的边长为（26+2-2x）m。

根据题意，得x（26+2-2x）=80。整理，得x2-14x+40=0。解得x1=4，x2=10。

答：这个矩形车棚相邻两边长分别为4m、20m或10m、8m。

【剖析】当x=4时，26+2-2x=26+2-2×4=20＞12，不符合题意，要舍去。错解忽视了问题的背景条件“墙的可用长度”。

【正解】设与墙垂直的边长为xm，则与墙平行的边长为（26+2-2x）m。

根据题意，得x（26+2-2x）=80。整理，得x2-14x+40=0。解得x1=4，x2=10。

当x=4时，26+2-2x=26+2-2×4=20＞12，不符合题意，舍去；

当x=10 时，26+2-2x=26+2-2×10=8＜12，符合题意。

答：这个矩形车棚相邻两边长分别为10m、8m。

【对策】遇到实际问题，在将其转化成数学问题并解决后，一定要将这个问题的解代回到实际问题中加以验证。

四、忽视问题中隐语发出的信息

例4某水果批发商场经销一种高档水果，如果每千克盈利10 元，每天可售出500 千克。经市场调查发现，在进货价不变的情况下，若每千克涨价1 元，日销售量将减少20 千克。现该商场要保证每天盈利6000 元，同时又要使顾客得到实惠，那么每千克应涨价多少元？

【错解】设每千克水果应涨价x元。

根据题意，得（500-20x）（10+x）=6000。解得x1=5，x2=10。

答：每千克水果应涨价5元或10元。

【剖析】我们容易找到等量关系：盈利额=每千克盈利×日销售量，但要注意有一句重要的隐语，“要使顾客得到实惠”。因此，我们在求出方程的两个解后，需要舍去x2=10 这个解，也就是说，既要涨价，也要让顾客得到实惠。

【正解】设每千克水果应涨价x元。

根据题意，得（500-20x）（10+x）=6000。

整理，得x2-15x+50=0。

解这个方程，得x1=5，x2=10。

要使顾客得到实惠，应取x=5。

答：每千克水果应涨价5元。

【对策】用方程解决问题，要充分利用题目中的已知条件，善于分析题目中的隐含条件，挖掘其隐含关系。