公交停靠站对社会车辆干扰影响机理及优化研究

苏少雄

(福建易华路信息技术有限公司,厦门 361026)

0 引言

巴士公共交通为低能耗、更环保的交通方式,比普通小汽车出行方式占用更少的道路空间.在中国大部分的城市地区,使用公共汽车出行的人群占比在整体上比使用其他出行方式的人群要少,但少部分地区例外,如北京中心城区的公交绿色出行比例超过60%[1].而在厦门市,在公众出行服务方面,“十四五”时期全市出行总量预期将增加至1 470万人次/d,2025年绿色出行占全方式71.2%、公交占机动化分担率51.8%,基本达到国家《绿色出行创建行动方案》制定的目标[3].

截止2020年底,厦门市人均小汽车保有量为0.35,远高于全国水平0.16[4].过高的人均汽车保有量是厦门市道路交通拥堵的主要原因之一,尤其在道路条件受限的地方,公交汽车停靠站和社会车辆共同占用1个进口道,当社会车辆占比过高、公共出行分担率较低时,二者间往往会出现严重的相互干扰,信号交叉口进出口范围内的此种干扰现象更为明显.因此各种公交车辆的专用车道配置问题逐步得到了关注.宋现敏等[5-6]以人均出行最短时间以及运载乘客总数量最大化为目标建立最优模型,结果表明,当社会车辆与公交车辆占比呈现特定占比时,公交优先策略具有最佳效益.在设置条件方面,王漫等[7-8]统计了公交车流量、社会机动车流量、公交车比例等参数值大小,建立了相应的机动车与公交车交织运行的速度模型,并以车辆出行总时间最短为目标建立优化模型,计算并改进了公交专用道的设置条件.

虽然公交专用道在减少社会车辆对公交车辆的干扰、提高公交车运行质量和服务水平等方面取得一定成效,但依然存在道路条件不足而导致车辆之间相互干扰的情况.在中国大部分城市交叉口进口道区域,公交停靠站常与社会车辆共用同一车道,发生冲突和车流干扰的风险通常都会增加[9-10].Zhao等[11]使用经过验证的仿真模型来研究进口道的直线式公交停靠站对机动车的干扰影响,发现公交车辆进出站时,社会车辆平均速度下降,公交车辆和社会车辆流量的大小对进口道通行能力都有显著影响.刘鹏等[12]分析了公交车辆在进站、停靠和出站过程中的延误情况,建立了道路机动车辆之间的干扰程度评估模型.部分研究者为解决进口道的排队延误拥堵问题,优化设计了公交停靠站的选址和位置,帮助建立有序的交通流,李力[13]探讨了在车流密度过大时的公交站点选址优化方法.马信辉[14]选取延误参数,建模并探讨公交停靠站的设置类型、站点的几何参数优化依据等,为停靠站的选址和改善提供了参考.

综上,为缓解进口道的公交停靠站周边拥堵和车辆干扰问题,大多数学者从社会车辆、公交车辆间以及非机动车等多种车流交织的角度出发,研究交通冲突、影响延误和交通风险等行为,结合停靠站点的选址问题,总结了以下内容:关于公交车辆和其他类型车的运行特性及属性参数;关于停靠站周边的延误和交通运行水平改进方法;关于站点的优化措施等.然而,关于社会车辆和公交车辆的干扰影响调查相比较车辆冲突调查更少.本文选取了进口道的公交停靠站为研究对象,研究该直线式站点的设计参数、交通流特性与车流干扰的关系,以降低车流间的干扰程度作为模型优化的目标,提出相应停靠站的优化方法.

1 数据收集与分析

1.1 调查站点类型

公交停靠站根据其在交叉口的位置可分为上游停靠站(Near-side busstops)、下游停靠站(Far-side busstops)和基本路段停靠站(Middle-block busstops)[15].本文选定的研究对象均为上游停靠站.上游停靠站的4种最常见的公交车站设置方式如图1所示,箭头为车辆的前行方向:1)在类型Ⅰ站点中,公交车辆停靠在非机动车道上,非机动车道与机动车道由地面标线进行隔离,公共汽车跨越地面实线进行停靠; 2)在类型Ⅱ站点中,公交车辆停靠在非机动车道上,非机动车道与机动车道通过隔离带进行物理分隔.当公交车辆停靠时,类型Ⅱ的车流之间干扰现象比Ⅰ更严重; 3)在类型Ⅲ站点中,公交车辆停靠在机动车道上,非机动车道与机动车道通过隔离带进行物理分隔,停靠站位于隔离带上; 4)在类型Ⅳ站点中,非机动车道与机动车道通过隔离带进行物理分隔,停靠站位于隔离带上.该站点属于港湾式停靠站,公交车辆停靠时位于港湾内的地带,不占用外部机动车道.

图1 常见公交停靠站类型:(a)类型Ⅰ (b)类型Ⅱ (c)类型Ⅲ (d)类型Ⅳ

本项研究中,选取类型Ⅲ的停靠站点为研究对象并收集数据.调查时间选取于2021-11—12周三、周四早晚高峰,时段分别取08:00—09:30、17:00—18:30,选取厦门市3个沿着进口道设置的直线式停靠站.调查排除了恶劣天气下的数据,所有站点均为单个泊位.采集的数据包含车道宽度、机动车流量、车辆速度、公交车站距离交叉口位置等参数.公交车辆和社会车辆的干扰状态分为3类:第1类为公交车辆由左侧车道驶入停靠站点,受右侧机动车道的社会车辆干扰;第2类为进入不可变道的区域前,公交车辆停靠时占用机动车道干扰后方社会车辆的变道;第3类为公交车辆加速离站时,与外侧绕行的社会车辆相互干扰.

1.2 数据关联分析

将车道宽度、停靠站与交叉口距离、车辆速度差异、交通量与3类车辆干扰情况利用回归分析法进行分析.

1.2.1 车道宽度与车流干扰关系

车道宽度与车流的干扰情况之间存在着部分相关关系,如图2所示.对2个影响因素展开多项式回归分析,3类干扰情况和车道宽度之间的变化关系显著:伴随着车道宽度的上升均表现为先降低再升高.对于第1类干扰,车道宽度在3.75 m时下降到最小,对于第2类、第3类干扰情况,在车道宽度为4.0 m时,均达到相应的最小数值.

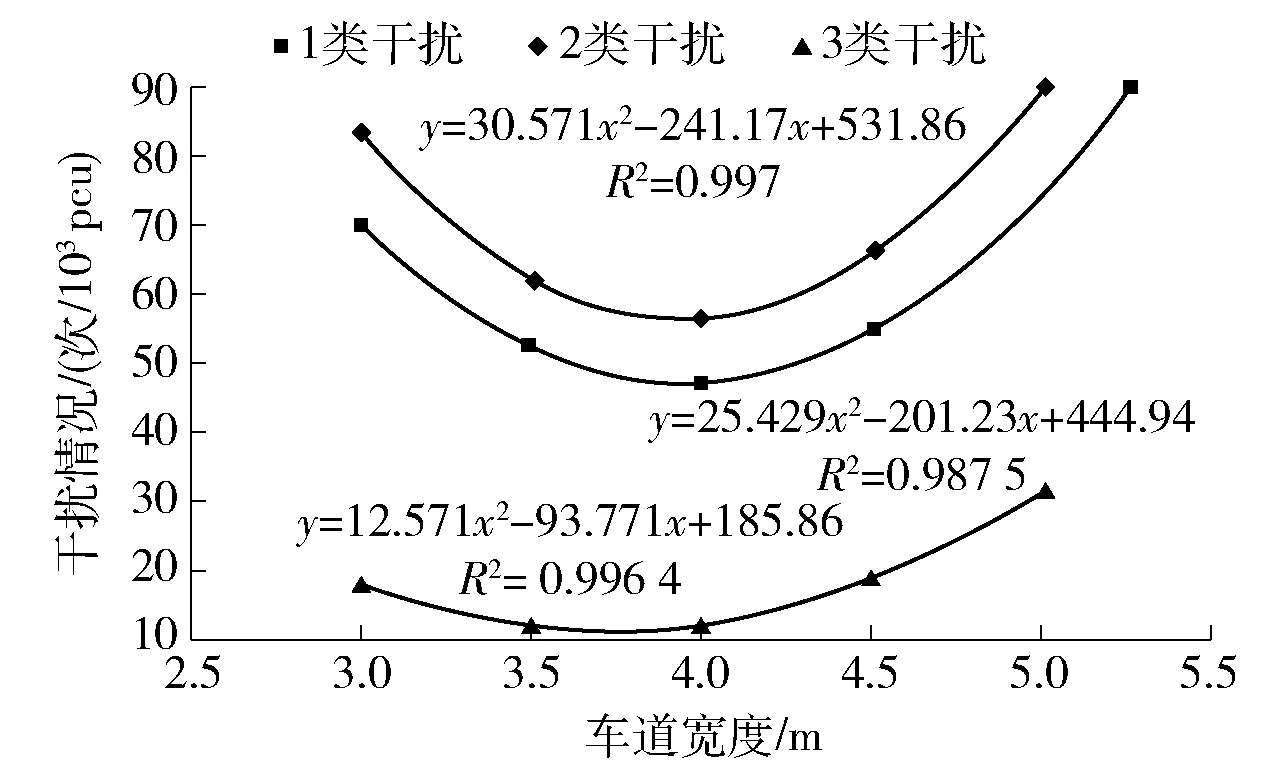
图2 干扰情况与车道宽度关系

1.2.2 停靠站距交叉口长度与车流干扰关系

停靠站距交叉口长度与车流干扰关系如图3所示.随着公交停靠站与交叉口距离的增加,3类干扰情况均表现为先降低再升高,且3类干扰均在距离交叉口约100 m左右最低.

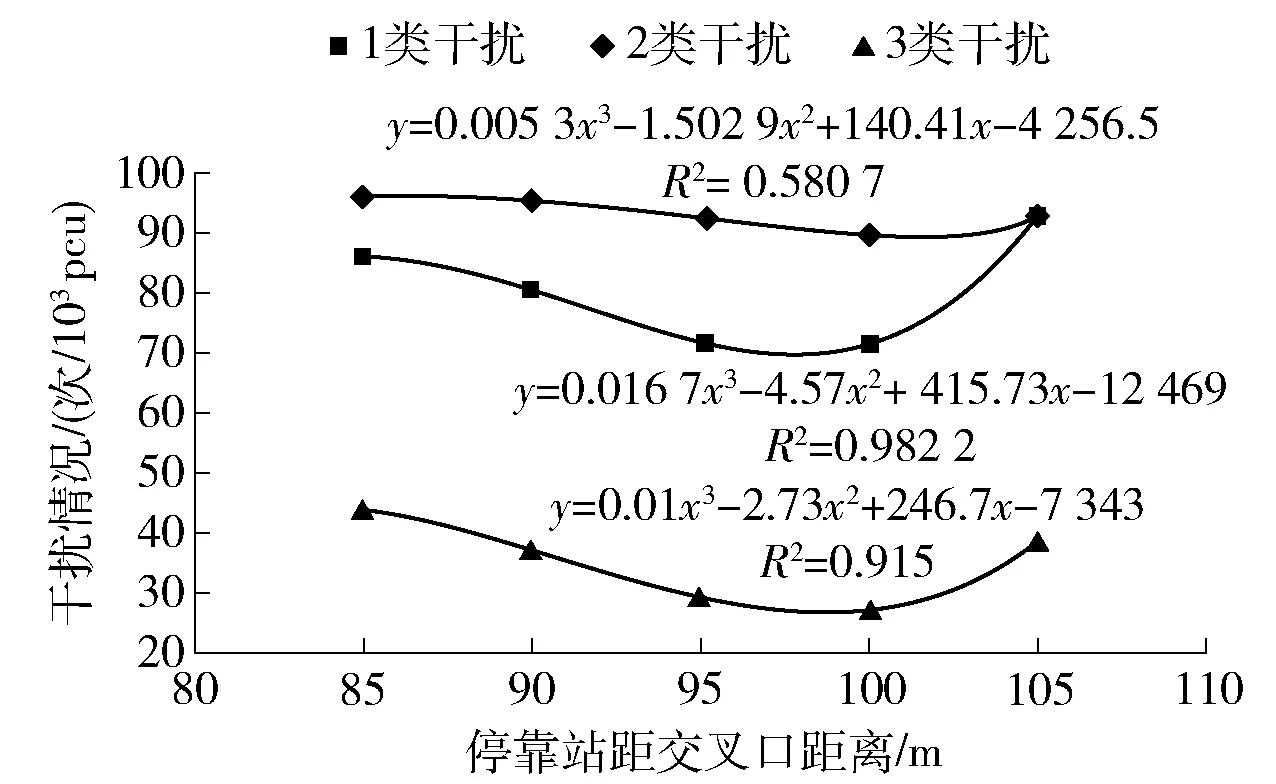
图3 干扰情况与停靠站距交叉口长度关系

图5 干扰情况与交通量关系

1.2.3 车辆速度差异与车流干扰关系

展开二阶多项回归分析,3类干扰的增长速度差异较大,其中第1类干扰与第3类干扰情况随着车速差异的增加而上升,且速度差异小于3 m/s时,第1类干扰的增长速度最快;速度差异高于该数值时,第1、3类干扰增长情况较为平缓.第2类干扰随着车速差异的增加先呈现微弱的降低随后增加的趋势,当速度差异为3.5 m/s时达到最低值.

1.2.4 干扰程度与交通流量的关系

展开二阶多项回归分析,所求解的3类干扰情况均呈现出随交通流量增加而增多的趋势.第1类干扰情况的增速拐点是500 pcu/h的交通量,到达该拐点之前的增速均较快;随后干扰情况变得平稳.随着交通量增加,第2、3类干扰的情况也呈现平缓增速.

2 车流干扰模型

2.1 干扰模型构建

以车道宽度、公交停靠站与交叉口的距离、公交车辆与社会车辆速度差异、交通流量为自变量,以第1类干扰情况、第2类干扰情况、第3类干扰情况为目标函数,建立两种车流间的干扰预测模型,见式(1).

y=a1f1(x1)+a2f2(x2)+a3f3(x3)+a4f(x4)

(1)

式中,x1为相邻车道宽度(m);x2为相邻车道的交通量(pcu/h);x3为车速差异(m/s);x4为公交停靠站距交叉口距离(m);f1,f2,f3,f4为相应影响因素的干扰函数;a1,a2,a3,a4为对应相关系数;y为所预测的干扰发生数值.选取调研数据中多组数据作为预测数据,得到3类车流的干扰情况如下.

第1类干扰模型根据式(1),用A表示相关系数,见式(2):

A=[a1,a2,a3,a4]

(2)

经过回归分析,得到第1类干扰的影响函数后,使用Matlab软件分析得到研究自变量和干扰情况的相关系数值,以第1类干扰为例,回归分析计算可得A的求解结果,最终得到公交车辆停靠站点时的第1类干扰模型如式(3)所示:

(3)

公交车辆停靠时的第2、3类干扰模型如式(4)、(5)所示.

(4)

(5)

2.2 验证模型

选取调查中除了用于建模以外的其他时段数据,用于模型验证见表1.

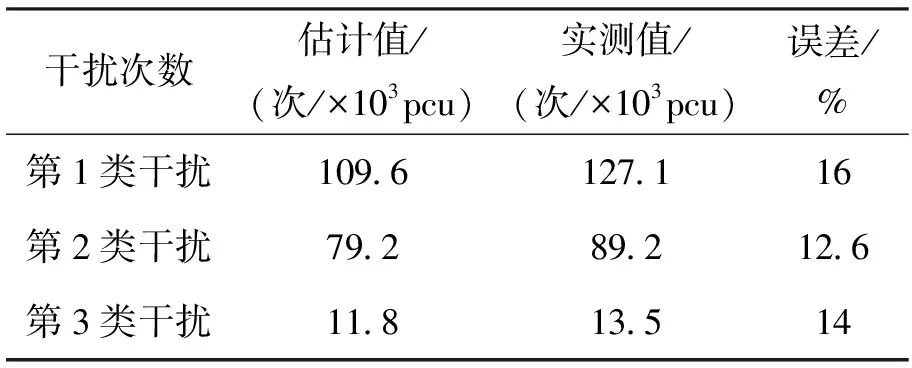
表1 公交停靠站交通干扰数值计算结果

在干扰情况的计算和分析结果中可能存在一定主观因素导致的误差,例如第1类误差较其余2类的数值更大,但考虑到所有误差值均低于20%,该模型结果可用于预测交通干扰的数值.

2.3 预测模型分析

使用python工具将数据导入并建立可视化模型,其中定义干扰发生次数的x区间为公交停靠站距交叉口距离;定义y区间为车道宽度;定义交通量为模型输入变量.考虑到灰度预测法可以处理不确定量或小样本量的系统,使用该方法得到车辆干扰的预测模型,可视化结果见图6.

图6 停靠站干扰预测模型

经1.2的计算分析结果可得,在与干扰程度相关的几个变量中,干扰程度最低时的交通量与速度差异分别是200 pcu/h和3.5 m/s,分别作为对应影响参数的取值.干扰程度最低时的公交停靠站距交叉口距离与车道宽度分别是100 m、4 m.结合图6数据的干扰次数为58,可认为满足了进口道停靠站的安全需求.

考虑到在实际条件中存在无法满足宽度需求等情况,该模型具有的优势在于数据呈现出的模型可调整空间较为充足,可以根据停靠站优化目标和进口道实际条件进行移动,选取其他次级优化方案.

2.4 停靠站延误分析

公交车辆位于进口道的停靠站时,占用该车道上直线式站点的整个泊车位,导致对相邻的车道运行产生较大干扰.停靠延误和多因素有较强的关联,当模型中的4个变量取干扰程度最低的对应数值时,停靠站的可靠程度最高,且相应的车均延误最低.

3 停靠站点干扰程度分析

3.1 车流干扰等级划分

本文对研究范围内公交停靠站点的车流干扰次数分析其累计百分频率,确定不同累计百分率对应的数值.引入公交停靠站周边的车流干扰程度可分为无干扰(A)、稳定(B)、临界稳定(C)、中等干扰(D)、严重干扰(E)该5个级别.统计发生干扰的总次数及累计频率曲线图,划分干扰等级如表2所示.

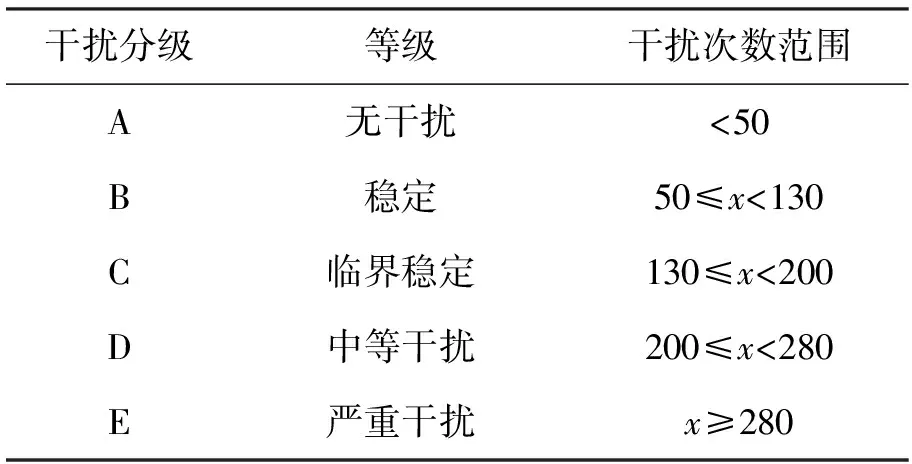
表2 干扰等级划分

3.2 干扰评价及预测

根据站点干扰程度回归模型和干扰等级划分情况.

以实际站点为例进行模型检验,选取市区内符合研究条件的直线式停靠站点进行数据统计与调查,站点位置特征及车流行驶特性调查结果见表3.

表3 站点调查情况

表4 实例公交停靠站干扰次数模型预测

表5 实例中山公园改进后干扰次数预测

综合站点的干扰情况分析,所选取的公交停靠站总干扰次数分别为138、196、264.根据车流干扰等级的划分,华盛路口处于稳定状态,高林居住区站处于临界稳定状态,中山公园处于中等干扰状态.

从实例分析的公交停靠站交通冲突率计算结果可知:中山公园站的第1、3类干扰占总体比例较高.结合实际道路情况、位置特征及车流行驶特性进行分析,该站点处于交叉口上游路段,道路断面为3幅路,临时拆除中央隔离带.路面机动车道宽度较窄,机动车与公交车辆行驶中容易相互干扰,甚至和对向车流发生冲突.部分机动车辆行驶速度较快时,加剧了第3类干扰情况的出现.综合上述情况提出对中山公园站的改善建议:①适当拓宽机动车道宽度,将 3.25 m拓宽为3.75 m;②适当增加公交停靠站距离交叉口停车线的长度,将50 m增加到80 m;③对机动车速度进行标志控制,不得高于30 m/s.中山公园停靠站改善后通过模型检测,干扰程度有明显的下降,干扰等级由中等干扰变为临界稳定,则说明以上停靠站点改进建议能够提高公交停靠站周边的交通稳定性.

3.3 站点优化措施

理想条件下的道路情况允许公交车辆和社会车辆共同行驶且互不干扰,充足的道路空间便于公交停靠站点优化,且有利于降低车流间的干扰程度.对于车道宽度的优化,通常从压缩道路绿化带的着手,必要时会占用道路边缘的人行道.

当下的站点服务水平不满足公交系统中车辆的安全和高效运行要求时,若站点周边的道路条件极为有限,导致不能实现港湾式停靠站点或其他形式的宽度改造,那么则需进一步结合该站点的位置布局、原公交路线运行效率、延误情况等因素进行评价,依据评价结果对该地区进行较大规模的路段重建措施,或选择将站点迁移至不严重影响原公交路线效率的、且存在改建空间的路段.

若当下站点周边道路的改造空间充分,允许大范围地修建和改造时,结合车流运行的稳定性分析,可将模型变量调整至干扰最低时对应的数值.

4 结论

1)伴随着车道宽度和公交停靠站与交叉口距离的增加,研究对象的3类干扰程度均表现为先减少后增大,且给出相应建议值:沿进口道设置的直线式单泊位公交停靠站距离交叉口的长度为80～110 m;车道宽度为3.5～3.75 m.

2)当公交车辆和社会车辆的整体交通量增加、车辆速度差异增加时,研究对象的3类干扰程度表现出连续增加的趋势,且给出相应建议值:公交车辆与社会车辆速度差异低于3 m/s,保障车道宽度维持在3.75～4 m,保障车辆闪避时有足够的行车空间和减少干扰,保障进口道的顺利通行避免拥堵发生.视距条件符合要求时,可以在交叉口增设减速标志等.

基于上述结论,在优化城市交叉口进口道上分布的公交停靠站时,基于站点周边道路和交通环境的综合考虑,可利用本文的车流干扰模型进行改造条件评估,在保持站点改造过程中不会影响停靠站运营和车辆行驶顺畅的同时,可节约改建成本,有利于城市公共交通发展.