高轨导航接收机的时钟辅助定位算法

郭坤昊, 葛 建, 陈夏兰, 房志博, 高 铭

(1. 中国科学院空天信息创新研究院, 北京 100094;2. 中国科学院大学电子电气与通信工程学院, 北京 100049)

0 引言

运行在地球静止轨道(geostationary orbit satellite, GEO)、倾斜地球同步轨道 (inclined geo-synchronous orbit,IGSO)的卫星的定轨通常需要依靠地面的测控网络实现。这种定轨方式成本高并且时效性差,如果能像运行在低地球轨道(low-Earth orbit,LEO)上的卫星那样,通过在星上搭载全球卫星导航系统(global navigation satellite system,GNSS)接收机,实现对卫星的定轨,将能为卫星发射和运行带来极大的便利[1]。适合在GEO、IGSO等卫星上工作的GNSS接收机属于高轨GNSS接收机,其典型工作高度高于一般导航卫星的轨道高度。

高轨GNSS接收机接收的导航卫星信号条件与地面和LEO卫星上的信号条件完全不同,主要表现在信号弱和几何构形差两个方面。

首先,GNSS卫星播发的导航信号是朝向地球发射的,全球定位系统(global positioning system,GPS)L1信号的双边主波束宽度大约是32°,仅能够覆盖地球及1000 km以下LEO卫星轨道[2]。高轨GNSS接收机恰好位于主瓣照射区域的机会非常小(如图1的红色区域)。如果仅使用导航卫星的主波束进行定位,即使用上GNSS星座的所有导航卫星,可用卫星数也很难达到4颗。为了有更多可用的导航卫星,高轨GNSS接收机的灵敏度通常做得很高,从而可以使用部分导航卫星的第1、第2旁瓣进行定位。但是,导航卫星的第1、第2旁瓣的信号功率在三维天线方向图的不同剖面上差异较大。即使在较强的剖面上,信号功率也要比主瓣低10 dB到20 dB[3]。此外,高轨接收机到导航卫星的距离大约是地面接收机的3倍左右,相应的自由空间传播损耗增加约10 dB。在距离因素和导航卫星的天线方向图因素的共同作用下,到达高轨GNSS接收机的信号功率比地面接收机低10 dB到30 dB[4]。

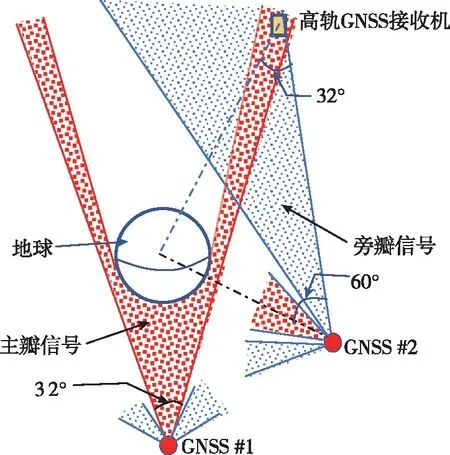
图1 高轨GNSS接收机的接收信号条件Fig.1 Reception conditions of high orbit GNSS receivers

其次,由于导航卫星旁瓣信号的覆盖区域,和地心形成的夹角最远有60°,在位于GEO的接收机的视角上,所有可用的导航卫星都分布在地球两侧距地心不超过32°的狭小区域内(如图1中高轨GNSS接收机与GNSS #2之间的相对关系),并且地心两侧10°的范围内,因地球遮挡和电离层的影响没有可用的导航卫星,这些导致接收机可见星的几何构形较差。姜慧等人的仿真实验表明对于运行在GEO轨道的高轨接收机利用北斗卫星导航系统(BeiDou satellite navigation system, BDS)定位时几何精度因子值(geometric dilution of precision, GDOP)均值约为49,其最大值约161;位置精度因子值(po-sition dilution of precision,PDOP)的均值约为35,其最大值约115[5]。

上述高轨GNSS接收机的信号条件最终反映在接收机性能上的表现是定位精度低、连续性差。

由于信号弱,高轨GNSS接收机典型的接收信号载噪比C/N0值在30(dB·Hz)左右,对应的码伪距测量精度大约在10 m左右,按PDOP值为35计算,由此导致的单历元解算误差大约350 m,远大于地面接收机的误差。同样由于信号弱,能够超过高轨GNSS接收机解调门限的导航卫星数较少。即使灵敏度较高的接收机,仍然存在可用卫星不足4颗的情况。秦红磊等人的仿真结果表明,接收机灵敏度阈值设为-175 dBW时GEO卫星可见GPS卫星数目在99%的运行时间里都不足4颗;而当接收功率阈值降低至-190 dBW时,虽然可见星数目明显增加,但2%的时间里可见星数目不足4颗[6]。

在较难改变信号接收功率和卫星几何构形的情况下,为了解决高轨GNSS接收机定位精度低和连续性差的问题,一些学者提出了轨道外推、卡尔曼滤波和深组合导航等适用于高轨GNSS接收机的算法。学者詹鹏宇对高轨场景下的导航定轨采用了无味卡尔曼滤波算法,还结合龙格-库塔方法的思想对扩展卡尔曼滤波算法进行了改进,并且对多种非线性滤波算法的高轨卫星定轨性能进行了对比分析[7];学者荆帅提出一种采用轨道外推器(orbit polating,OP)与GNSS观测量进行深组合的方案,在测距域内重新构造GNSS/OP深组合滤波器,把传统的解析式外推器或数值积分式外推器改进成一种简化的基于经验加速度模型辅助的四阶龙格库塔积分器,并选择了GNSS空间服务域(sp-ace service volume,SSV)用户-高椭圆轨道(highly elliptical orbit,HEO)飞行器作为测试对象,仿真验证了GNSS/OP深组合方案的性能[8];学者林魁提出了融合 GNSS 与相对测量的序贯博弈自主定轨方法。基于SSV多星任务需求,利用高精度星间测量进一步提高航天器自主定轨精度,针对分布式系统中因状态估计间的互相关关系导致滤波发散问题,提出了一种序贯博弈优化算法,并以四颗GEO卫星任务为例对算法进行了验证[9]。

以上算法都存在运算量大的问题并且存在一定的适用条件。例如,学者詹鹏提出的利用卡尔曼滤波器作为时钟“驯服-守时”模型的算法,虽然精度较高,但是算法实现时滤波器的协方差矩阵和状态转移矩阵等初始化存在困难;学者林魁提出的序贯博弈自主定轨方法由于需要星间链路支撑和多用户之间建立星间链路,适用于多个用户间高精度的定轨需求。本文提出利用接收机恒温晶振的频率稳定性抑制观测噪声,以较小的运算量显著地改善高轨接收机定位的连续性和精度,图2为流程图。

图2 算法流程图Fig.2 Flowchart of the algorithm

1 时钟辅助定位算法流程

1.1 算法概述

接收机硬件各通道跟踪导航卫星信号所获得的星上时观测量ts(上标S表示导航卫星的序号)作为本算法的原始输入,经图2所示的流程计算,最终得到接收机位置矢量[x,y,z]的解算结果。图2中“伪距构建”、“钟差解算”和“时间维持”3个模块构成了时间维持环路,用于产生历元时间的优化预测值tk(下标k为观测历元的序号)。本算法需要用恒温晶振(oven controlled crystal oscillator,OCXO)等稳定性高的频率源维持历元时间间隔的稳定。

1.2 伪距构建

接收机通过对测距码相位的观测获取卫星信号离开导航卫星的时间,即星上时ts。接收机在第k个历元同时观测到N个导航卫星信号的发射时间构成观测值输入矢量[t1,t2,…,tN]k。根据接收机的历元时刻tk和观测到的星上时ts可构造第S颗卫星的伪距ρs,其表达式如下

ρs=c·(tk-ts)

(1)

其中,c为光速,所观测的N颗卫星的伪距构建成伪距观测值矢量[ρ1,ρ2,…,ρN]k。

1.3 钟差解算

“钟差解算模块”用来估计tk与导航系统真实时间之间的偏差δtk。

在N≥4,并且时间精度因子值(time dilution of precision,TDOP)小于某个预先设定的阈值(比如60)的条件下,通过求解方程组(2),获得δtk的估计值。

(2)

方程组(2)中,[xs,ys,zs]表示第S颗卫星的位置矢量,该矢量可以根据卫星星历和信号发射时刻ts计算得到。[x,y,z]是待求的接收机位置矢量。由方程组(2)解出的接收机位置包含较多噪声,当时间维持模块进入稳态后,就不再使用方程组(2)解出的位置。

1.4 时间维持

1.4.1 时间维持模块的正常运行状态

当钟差解算模块输出的δtk有效时,时间维持模块需根据带有较大噪声的钟差估计值δtk不断修正本地钟差和钟漂参数,尽可能维持本地时间的准确[10]。

尽管可以采用高阶比例积分微分控制器(proportion-integral-derivative,PID)算法[11]或者卡尔曼滤波算法[12]进一步提升性能,但实验表明,对于充分老化的OCXO而言,简单的二阶锁相环算法就能获得相当满意的效果[13]。具体迭代步骤如式(3)和式(4)所示

tk+1=tk+Ts+dk+C1·δtk

(3)

dk+1=dk+C2·δtk

(4)

其中,Ts代表观测历元时间间隔的标称值,dk是第k历元接收机钟漂的估计值。

式(3)和式(4)中,参数C1和C2是二阶锁相环的环路参数[14],它们是由环路的阻尼系数和噪声带宽共同决定的。其中,C1和C2与环路自然频率ωn、阻尼系数ξ的关系分别如式(5)和式(6)所示

(5)

(6)

而ωn和ξ又决定了环路的噪声带宽BL,其关系如式(7)

(7)

ξ通常取值为0.707,BL的选择对算法性能的影响最为明显,与GPS驯服恒温晶振(GPSDO)类似,BL可以设计得非常小。考察方程组(2),由于卫星的高动态,等号左边[xs,ys,zs]和[x,y,z]的真值都存在较大动态,而δtk的真值则仅包含由恒温晶振阿伦方差导致的极小动态。等号右边的伪距ρs则包含了卫星动态和恒温晶振动态之和。接收机的码跟踪环需要维持对ρs的跟踪,因此码跟踪环的噪声带宽Bn需要设置在2 Hz左右。经方程组(2)解出的δtk已剥离了卫星的高动态,所以时间维持环的噪声带宽可以做得很窄。利用GNSS模拟器模拟多种轨道场景的测试表明,如果采用OCXO做频率源,即使将BL设为0.001 Hz,本算法仍可以很稳定地工作。

1.4.2 时间维持环路的初始化

式(3)和式(4)为迭代公式,初值d0可设为0,也可以将接收机上一次运行时dk的收敛值作为本次运行的初值。初值t0需要利用观测到的某个导航星的星上时ts加上一个预估的传播时延作为初始尝试值,并利用第1次解得的钟差值δt0修正得到t0的迭代初值。

1.4.3 时间维持模块的守时状态

迭代过程中,如果某个历元可观测卫星数N<4,或者TDOP大于设定的阈值,则钟差观测值δtk不可用,时间维持模块按δtk=0继续迭代运行。此时时间维持模块处于守时状态。在环路已收敛的条件下,OCXO的稳定性越好,则时间维持模块可连续守时的时间就越长。

1.5 定位解算

时间维持模块进入稳定状态后,其输出的历元时间tk是对当前历元的GNSS时的优化估计,通常比单点解算得到的GNSS时间更准确(见本文2.2节)。因此,按式(1)构造的伪距ρs非常接近接收机和导航卫星之间的真距。因此,在定位解算模块中,通过求解不带钟差的方程组(8),得到关于接收机位置矢量[x,y,z]的优化估计。

(8)

应注意到,即使在N=3的情况下,方程组(8)依然能够维持定位解算。

2 时钟辅助算法的精度

2.1 高轨GNSS接收机的主要误差源

GNSS接收机的定位误差由测距误差(user equivalent range error,UERE)和所观测卫星的几何构形共同决定。其中UERE又分为用户测距误差(user range error,URE)和用户设备误差(user equipment error,UEE)两部分[16]。

URE主要包含导航卫星的星钟误差和轨道误差以及电离层误差和对流层误差。对于高轨GNSS接收机而言,由于信号穿越电离层和对流层的时段占整个可视时段的比例很小,可以在选星策略中排除这些时段的观测量,因此可以只考虑导航卫星的星钟误差和轨道误差。这些误差由卫星导航系统运控的精度决定。许多的实测数据表明钟差和轨道误差导致的URE精度在1.0 m(1σ)左右[17]。

URE的值是缓变的,在几分钟的时间范围内,同一颗导航卫星的URE值几乎为一个常数。

UEE主要包含接收机热噪声和多径干扰。对于高轨 GNSS 接收机而言, 可以通过合理的天线布局等方法极大地减轻多径的影响。因此,这里只考虑热噪声的影响。由热噪声导致的码伪距测量误差可由式(9)估算[18]。热噪声标准差σDLL和输入信号载噪比的数学关系如式(9)所示

σDLL=λL·

(9)

其中,λL(m)表示测距码码片宽度;D(码片数)表示相关器的间距;Bfe(Hz)表示双边前端带宽;Tc表示码片周期且Tc=1/Rc,Rc是码片速率。由于高轨GNSS接收机接收的导航信号十分微弱,导致热噪声误差可达10m左右。在高轨条件下,热噪声误差是接收机最主要的误差源。

UEE的值是快变的。如果接收机的历元间隔大于1/(2·Bn),可以认为不同历元间的热噪声测量误差是相互独立的,并且UEE与URE之间是相互独立的。

此外,由热噪声导致的测量误差UEE是0均值的。

2.2 tk误差

与方程组(2)相对应,第k个历元各星URE和UEE的瞬时值分别可构造成误差列矢量UREk和UEEk,则第k个历元的解算误差[exk,eyk,ezk,C·eδtk]T可表示为式(10)

(10)

其中,G′为方程组(2)线性化后的系数矩阵。

方程(10)为线性方程,所以δtk的解算误差序列eδtk可表示为由UREk导致的误差序列eδtURE,k和由UEEk导致的误差序列eδtUEE,k之和,如式(11)所示

eδtk=eδtURE,k+eδtUEE,k

(11)

由于各星URE值是缓变的,G′由卫星的几何构形决定,也是缓变量,所以eδtURE,k是缓变量,其值在数分钟内保持恒定。而UEE是0均值快变量,所以eδtUEE,k也是0均值的快变量。即eδtUEE,k的功率谱在区间[0,1/Ts]上近似均匀分布。

时间维持模块中的迭代式(3)、(4)对输入序列δtk和输出序列tk而言构成线性系统。因此,由δtk上的误差eδtk传递到tk的误差etk也符合线性系统的响应关系,如式(12)所示

etk=etURE,k+etUEE,k

(12)

其中,etURE,k为eδtURE,k经锁相环传递到本地历元时间估计值tk上的误差分量。由于eδtURE,k在环路响应的相关时间长度内几乎为常数,所以,etURE,k≈eδtURE,k。而etUEE,k为eδtUEE,k经锁相环传递到本地历元时间估计值tk上的误差分量。对噪声而言,锁相环表现为一个带宽为BL的低通滤波器[19]。即eδtUEE,k的噪声谱中仅有[0,BL]和[(1/Ts)-BL,1/Ts]两部分能量能通过环路而到达etUEE,k。因为eδtUEE,k是0均值的,所以etUEE,k也是0均值的。如果BL设计得比较小,以至于相对etURE,k而言,etUEE,k≈0。即etk≈etURE,k≈eδtURE,k。进而,tk的标准差σt即etk的标准差,近似等于eδtURE,k的标准差。根据GNSS接收机误差传递的基本理论,在BL足够小的条件下,σt的表达式如式(13)所示

σt=TDOP·σURE

(13)

其中,σURE为测距误差中URE分量的标准差。

2.3 定位误差值

对误差传递而言,图2所示算法流程的各模块均为线性系统。因此,从星上时的观测误差到最终的解算误差之间的传递也满足线性关系。我们可以分别讨论URE和UEE对最终定位误差的影响。

2.3.1 URE导致的定位误差

观测量ts中的URE误差到最终定位误差的传播路径为:

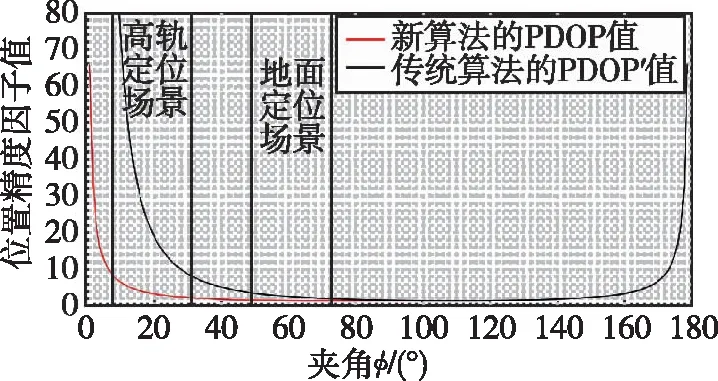
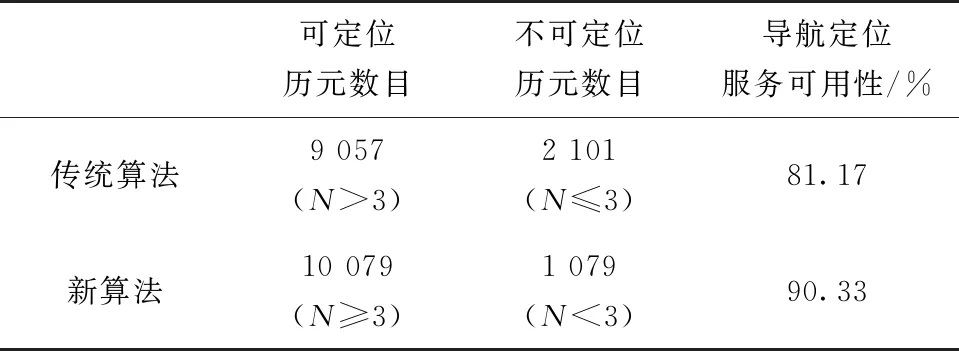
首先,历史的观测误差矢量序列UREm(m

接下来,etk和UREk共同通过方程组(8)传递到位置解算结果上,形成由URE导致的误差分量ePURE,k。

由于各星URE值在几分钟的时间内保持不变,可以认为UREm≈UREk。这样,对于URE误差分量的传播而言,方程组(8)与方程组(2)为同解方程。因此,ePURE,k的标准差σP,URE如式(14)所示

σP,URE=PDOP′·σURE

(14)

其中,PDOP′为与G′对应的位置精度因子。

2.3.2 UEE导致的定位误差

根据2.2节的讨论,当时间维持模块的噪声带宽足够小时,tk中不包含UEE所导致的误差分量。因此,观测量ts中的UEE误差直接通过方程组(8)传递到最终定位误差。

设第k个历元的定位结果中由UEE导致的误差分量为ePUEE,k,其标准差σP,UEE如式(15)所示

σP,UEE=PDOP·σUEE

(15)

其中,PDOP为与方程组(8)线性化后的系数矩阵G对应的位置精度因子。

2.3.3 总定位误差

根据线性系统理论,总定位误差的瞬时值序列ePk为由URE导致的误差分量序列ePURE,k和由UEE导致的误差分量序列ePUEE,k之和如式(16)所示

ePk=ePURE,k+ePUEE,k

(16)

由于URE和UEE两者的取值是相互独立的, 所以ePURE ,k和ePUEE ,k两者的取值也是相互独立的。本文所提算法的定位误差ePk的标准差σP可表示为式(17)

=(PDOP′·σURE)2+(PDOP·σUEE)2

(17)

式(17)第1项,由URE导致的定位误差,与常规导航解算方法完全相同。而第2项,由UEE导致的定位误差,与PDOP有关。在高轨场景下,UEE取值远大于URE的值,因此PDOP的大小决定了本算法的性能。

2.3.4 位置精度因子值

PDOP′由方程组(2)线性化后的系数矩阵G′决定。而PDOP由方程组(8)线性化后的系数矩阵G决定。考察这两个方程组,G′和G存在以下关系:G′=[GN],其中,N为各元素为1的列矢量,其行数与G的行数相等。

PDOP′由G′的权系数矩阵H′对角线的前3项导出。而PDOP由G的权系数矩阵H对角线的3个元素导出。其中

H′=(G′T·G′)-1

(18)

H=(GT·G)-1

(19)

利用实对称矩阵的特性和柯西不等式可以证明,对于任意的星座构形,一定存在以下关系:PDOP≤PDOP′。即本算法能够通过消减UEE的影响而改善定位精度。

为了进一步考察本算法对定位精度的改善程度,考虑以下算例。

假设接收机刚好接收到4颗导航卫星的信号, 其中1号卫星距地球最近,其余3颗卫星到1号卫星的夹角相同,均为φ,并且均匀分布在1号星的周围,如图3所示。

图3 PDOP和PDOP’算例模型的空间构型图Fig.3 Spatial configuration diagram of PDOP and PDOP’ example models

计算φ从1°到179°范围内对应的PDOP′和PDOP值,如图4所示。

图4 PDOP和PDOP’随φ的变化Fig.4 The value of PDOP and PDOP’ with respect to φ

考察图4,首先注意到PDOP曲线始终在PDOP′曲线下方,这与之前的分析相符。当φ等于arccos(-1/3)时,PDOP与PDOP′同时取得最小值1.5。

根据引言部分的分析,高轨接收机可见的导航卫星距地心的夹角一般不超过32°,如图4中“高轨定位场景”所示区间。可见,在这个区间,PDOP仅为PDOP′的1/4～1/10,本算法有显著的精度优势。

对应地面接收机而言,可视卫星分布在高度角50°～90°范围中, 对应图4中“地面定位场景” 所示区间。可见, 本文提出的算法对地面应用价值不大(并且, 在地面场景中UEE的值也不大)。

3 高轨场景下算法的仿真

通过仿真,进一步验证了本算法在高轨场景下的定位精度和定位的连续性。

3.1 高轨场景的搭建

(1)用户轨道数据

从2021年10月26日9时整开始,根据实践十七号卫星实测导航数据为参考,利用实时更新且准确的BDS导航星座进行仿真。其中高轨GNSS接收机运行轨道的半长轴约为44 379 km。

(2)GNSS星座构形

以同期BDS星座的实际星历文件作为接收机观测的GNSS星座。

(3)导航发射信号强度

发射卫星方向图按照下图5所示进行设置[20-21]。

图5 发射卫星天线方向图设置Fig.5 The Configuration of satellite antenna direction chart

接收机接收信号功率Pr和发射信号功率PT的关系见式(20)

Pr=PT+GT-L+GR

(20)

其中,GT是发射天线增益,GR是接收天线的增益,通常GR=0 dB,L表示导航信号传输损耗。仿真系统根据每个历元上的导航卫星位置和接收机位置分别计算传输损耗L和发射天线的方向性增益GT。由PT、GT、L及GR等参数,得到Pr。Pr和接收信号载噪比C/N0的关系为:C/N0=Pr-Nr,Nr是接收机噪声功率谱密度,取值为-205 dBW/Hz。

仿真中高轨GNSS接收机灵敏度设置为-177 dBW,对应的C/N0的门限值为28。

(4)观测量误差模型

第1步:仿真系统按历元间隔1 s产生无误差的导航星和接收机之间距离的仿真数据;

第2步:在距离仿真数据上叠加一个OCXO钟差的实测数据。该数据是以铯钟为基准,用时间间隔计数器测量获得的;

第3步:在第2步基础上添加URE和UEE两种噪声。

URE的构造方法:产生一个服从(0,σURE)高斯分布的随机数分配给各个导航卫星, 在仿真期间各星的 URE 的取值保持不变。σURE取1.0 m。

UEE的构造方法:每个历元对每颗卫星单独产生一个服从(0,σDLL)高斯分布的 UEE噪声。其中的σDLL是根据各星在该历元的C/N0仿真结果按式(9)计算得到的。

(5)定位误差和定位连续性统计

接收机模型在每个历元上选择C/N0超过阈值的导航卫星的仿真数据按图2所示流程进行计算。分别统计方程组(2)和方程组(8)的解算结果,作为常规算法和本文提出的算法的结果。

3.2 仿真结果

3.2.1 导航定位服务的可用性

定义导航定位服务的可用性,即高轨场景下定位服务的可用性=高轨场景下定位算法可定位历元时间/总观测历元时间×100%。两种算法定位服务的可用性情况如表1所示,可用性的改善主要是因为可用卫星数等于3的情况在仿真时段内占据一定比例(图6中N=3的区间)。

表1 两种算法定位服务的可用性情况

1) 常规算法。可定位的历元所占比例为81.17%。2) 高轨时钟辅助定位算法。新算法可定位的历元所占比例为90.33%。3) 由1)和2)可见,新算法提高了导航定位服务的可用性。

3.2.2 定位时段精度

利用式(21)评估定位精度值ΔP

(21)

其中,Δkx、Δky、Δkz分别表示第k个历元接收机三维坐标的误差值。

两种算法误差值ΔP的变化情况如图6所示。由表2可见:在高轨场景下,本文提出的时钟辅助定位算法的精度明显优于常规算法。

图6 定位历元时段内定位误差值变化情况Fig.6 Change of positioning error values during positioning epoch period

可见,传统算法单历元解算误差最大值的数量级为102m;统计后发现:新算法单历元定位误差最大值约为15 m左右,新算法单历元定位误差值ΔP大幅减小。

两种算法定位误差的标准差如表2所示。

表2 定位误差标准差仿真和理论值

4 结论

本文提出一种高轨卫星导航接收机时钟辅助定位算法,利用OCXO的稳定性降低了UEE噪声对定位精度的影响。理论和仿真试验表明,本文所提的算法特别适用于高轨导航接收机的应用场景,典型的码伪距定位误差最大值可从常规方法的150 m左右改善到不超过15 m,并且本算法能够在可用卫星仅3颗的条件下维持一段时间的定位解算,因此也能在一定程度上改善高轨导航接收机的定位连续性,但对低轨和地面等应用场景,本算法的效果并不显著。

本文仅从时钟辅助的角度改善高轨卫星导航接收机的性能,尚不能完全解决高轨卫星导航接收机所面临的接收信号弱的问题,工程上还需要综合运用惯性深组合、矢量跟踪等技术,才能满足实用化的要求。