面向室内场景的惯性磁感应定位方法
2023-09-27夏子权李新年于谦玺冯学光李清华
夏子权, 李新年, 闻 帆, 于谦玺, 冯学光, 李清华
(1.哈尔滨工业大学空间控制与惯性技术研究中心, 哈尔滨 150001;2.中国人民解放军32380部队, 北京 100072)
0 引言
近年来,随着智能无人系统、物联网等技术在室内环境的应用,人们对室内导航定位技术提出了更高的要求,低成本、高精度且易于维护的室内导航定位方案是室内导航技术领域重点研究方向之一[1-2]。在卫星导航拒止的室内环境中,UWB、视觉、激光雷达及惯性导航等方法由于环境约束和自身因素,无法长时间提供高精度的可靠导航定位服务,利用低频旋转磁场的高穿透力和特征矢量方向不变的特性,可为室内等复杂场景提供一种高精度、无积累误差的导航定位方案[3-4]。通过使用通电线圈或旋转永磁体等人工磁信标可生成规律性的低频旋转磁场,结合磁传感器测量值与相对位置间的数值关系,可以获得高精度的定位解算结果[5-7]。
目前,针对室内环境下的磁信标定位技术,国内外学者已开展了大量研究,研究内容主要围绕基于磁场强度、磁场矢量和指纹匹配的定位技术3个方面展开[8-14]。Darmindra D. Arumugam等人[8-9]开发了一种远程低频磁场静态定位技术,通过解耦磁场强度和距离间的关系进行测距,在室内环境下利用两个磁信标实现了高精度的二维定位;Bo We等人[10-11]利用在空间中选取一定数量的指纹特征匹配点,记录对应的感应磁场强度,在实际导航中通过匹配测量点和指纹点处的磁场强度来实现目标定位,并结合惯性导航开发了一套iMag+SLAM系统,以满足室外和室内环境中精确定位和快速设置的要求;李新年等人[12-14]根据旋转磁场具有唯一方向不变的特征矢量的特点,建立了特征矢量与位置间的数学关系,仅依靠磁场矢量便可实现定位功能,在此基础上提出了一种不受传感器姿态误差影响的惯性磁感应定位方法,有效解决了定位过程中磁传感器姿态对结果的影响。然而,上述3种方法都存在共同的缺点:需提前确定信标的磁矩信息,对于大小呈正弦变化的磁矩,只有获得整个周期的数据才能确定其大小,这大大降低了定位结果的输出频率,增加了磁信标部署的难度。
为了降低人工磁信标定位系统的部署难度、提高系统的输出频率,本文建立了一种不受磁信标磁矩信息和传感器姿态影响的磁感应矢量夹角观测模型;结合惯性导航的误差模型,提出了一种的惯性磁感应动态定位方法,并利用无迹卡尔曼滤波[15,17](unscented Kalman filter, UKF)算法实现了磁场数据和惯导数据的同步融合,有效提高了导航精度。
1 磁感应定位模型
1.1 基于磁感应矢量夹角的观测模型
人工磁信标定位系统主要由磁场信号发射机、接收机与导航解算模块3部分构成,如图1所示,磁场信号发射机由两个通入不同频率正弦激励电流的正交线圈构成;接收机由3个正交的感应线圈构成,利用3个线圈上感应电动势的变化实现对发射机磁场矢量的测量;导航解算模块则根据接收机的磁场矢量测量值进行信号处理,结合导航算法实现对目标点处的快速定位。

图1 人工磁信标定位系统示意图Fig.1 Schematic diagram of artificial magnetic beacon positioning system
将由双轴正交螺线管构成的磁信标作为磁场信号发射机,分析其磁场分布规律。根据我们之前的研究[13-14],当接收机与发射机之间的距离r大于发射机线圈半径R的3倍时,可将发射机的线圈等效为两个正交的磁偶极子,根据毕奥-萨伐尔定律,磁偶极子的磁场矢量可以表示为
(1)
式中,μ0=4π×10-7H/m,表示空间环境的磁导率;r表示接收机与发射机之间的距离;m表示磁矩矢量。
双轴磁信标的两个发射线圈Tx1和Tx2的线圈匝数为Nc和Ns,磁通面积为Sc和Ss,分别通入幅值为Ic和Is、信号频率为ωC和ωS,且相位相差60°的正弦激励电流,根据图1和式(1),可以得到线圈Tx1和Tx2在空间中任意一点处P(r,φ,θ)磁场矢量BC和BS的表达式
(2)
(3)
式(2)和(3)中,MC=ICNCSCsin(ωCt)和MS=ISNSSSsin(ωSt+60°)分别表示发射线圈Tx1和Tx2的磁矩;φ和θ分别为接收机相对于发射机的俯仰角和方位角。


(4)

(5)
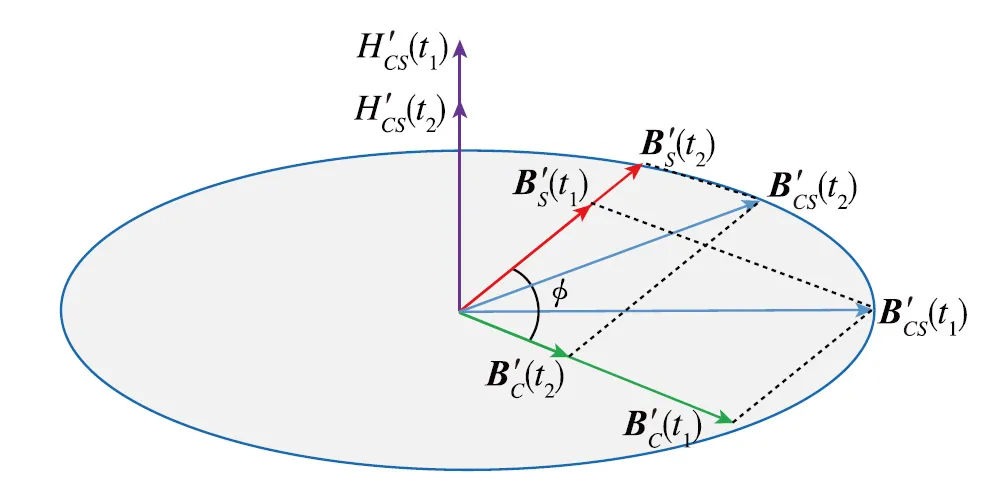
图2 旋转磁场示意图Fig.2 Schematic diagram of rotating magnetic field

(6)
(7)
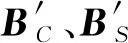
(8)
(9)
基于式(8)和式(9),可以构建如下观测模型
(10)
分析式(10)可知,该观测模型直接利用测量得到的磁感应矢量夹角余、正弦值作为量测量,可以配合其他传感器如惯性传感器进行组合导航。
1.2 基于UKF的惯性磁感应定位模型
一般情况下,室内环境中使用的低成本MEMS惯导系统总是在小范围内运动,因此选择当地直角坐标系作为导航参考坐标系(n系),导航起点为坐标原点(O),磁信标两正交轴的轴向为Oxn和Oyn,垂直xOy平面向上为Ozn,建立惯导系统的误差方程
(11)
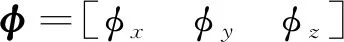
在惯导系统误差方程和磁感应矢量夹角观测模型的基础上,构建惯性磁感应定位系统的状态空间模型
(12)

Fk/k-1=
(13)
根据式(12)可知,利用磁感应矢量夹角辅助惯导对动态目标进行定位的模型是非线性的。目前,针对非线性模型的滤波方法,常用的有扩展卡尔曼滤波(EKF)和无迹卡尔曼滤波(UKF)[17]。EKF算法基本思想是先对非线性函数进行泰勒展开,然后保存展开式的一阶项,忽略其余高阶项,将非线性系统近似为线性系统,最后再完成卡尔曼滤波估计;UKF是一种对后验概率密度进行近似而得到的滤波算法,可直接对系统导航参数进行估计,从而避免对非线性量测方程线性化,保证了系统具有较高的定位精度,因此本文采用UKF完成对惯导和磁场数据的融合。
针对本文建立的惯性磁感应定位模型,给出以下UKF滤波流程。
Step1 初始化状态量和协方差矩阵
(14)
Step2 进行Sigma采样,计算采样点
(15)
Step3 时间更新
(16)
式中,Wi,e和Wi,c分别为UT变换中计算Sigma采样点对应的均值和协方差权值,定义为
(17)
其中,τ=α2(n+γ)-n为缩放比例参数;n为状态量的维数,本文中n=15;α控制由非线性函数带来的高阶影响,一般取e-4≤α≤1,γ=3-n,β=2。
Step4:量测更新
(18)
Step5:状态和协方差估计更新
(19)
(20)
2 实验验证
通过上述分析,本文建立了基于双轴磁信标的磁感应矢量夹角观测模型和基于UKF的惯性磁感应定位模型,本章将通过实验的方式分别对两个模型的有效性和精度进行验证。由于实际实验过程中很难给出运动目标的真实动态轨迹,因此本章将采用数值仿真的方式对基于UKF的惯性磁感应定位模型进行仿真验证,通过对比真实轨迹和实际运动轨迹,从而达到验证该模型精度的目的。
2.1 基于磁感应矢量夹角的观测模型实验验证
本节将利用如图3所示的双轴磁信标实验系统测试基于磁感应矢量夹角观测模型的精度和稳定性,该系统由激励电流生成器、功率放大器、双轴磁场发射机、三轴矢量磁传感器和磁场数据处理模块5个单元组成。

图3 磁信标实验系统Fig.3 Magnetic beacon experimental system
实验时,首先确定导航参考坐标系(n)和测量点坐标,本实验以双轴磁场发射机的几何中心为坐标原点(O),两正交轴指向分别为x和y方向,垂直xOy平面指向下为z方向,在该坐标系下按照接收机与发射机间距离由近及远的原则选择9个实验点,测得其坐标值,位置点和坐标如图3所示;其次,磁场发射机的两个线圈中分别通入幅值2 A、频率20 Hz和30 Hz、相位相差60°的激励电流,此时空间中生成旋转磁场;然后,将感知范围为0.1~10 000 nT 的三轴矢量磁传感器分别放置于9个实验点,测得实验点处的磁场数据;最后,利用式(8)和(9)分别计算出磁感应矢量夹角余、正弦值的理论值和实验值。为了测试传感器姿态和环境中遮挡物对精度的影响以及实验结果的稳定性,设计以下3组实验,并且每组实验重复10次。
实验1:将磁传感器分别放置于9个实验点处,保证发射线圈和磁传感器处于同一坐标系下,两者间无遮挡物,测量此时磁场数据。
实验2:控制磁传感器相对于发射线圈的俯仰角、横滚角和航向角分别为20°,30°和40°,其他同实验1。
实验3:在发射线圈上覆盖住一个木箱,其他同实验1。
实验结果如图4所示,从误差图中可知,不同位置处磁感应矢量夹角余弦值和正弦值的理论值与3组实验值之间的最大误差值均小于0.1,且3组实验值之间的误差值小于0.05,说明传感器姿态以及环境中遮挡物对磁感应定位结果并无影响;从误差棒图中可以看出,每组实验重复10次的标准差小于0.08,离散程度较小,说明实验结果具有较高的稳定性,且变化的磁矩对磁感应定位并无影响。需注意的是随着接收机和发射机之间距离的增大,数据的离散程度有增大的趋势,这是由于磁场信号强度随距离衰减导致信噪比下降引起的,说明距离是影响测量精度的重要因素。

(a)

(b)图4 不同位置处磁感应矢量夹角余弦值和正弦值的误差大小及稳定性分析结果图Fig.4 Error and stability analysis result of the cosine and sine values of the included angle of the magnetic-induction vector at different positions
2.2 惯性磁感应定位模型仿真验证
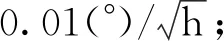

图5 基于UKF的惯性磁感应定位结果Fig.5 Results of inertial magnetic-induction positioning based on UKF
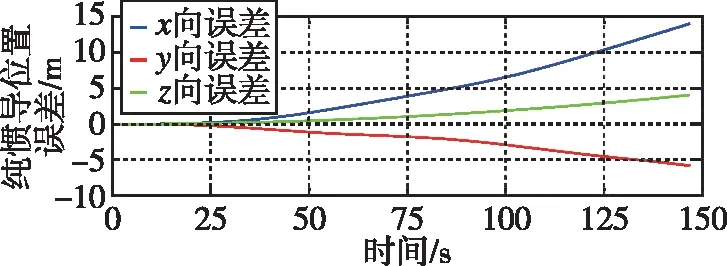
图6 纯惯性位置误差图Fig.6 Inertia position error diagram
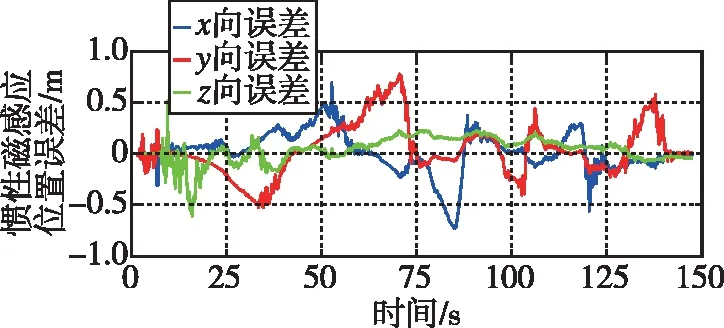
图7 惯性磁感应组合导航位置误差图Fig.7 Position error diagram of inertial magnetic-induction integrated navigation
从仿真的结果可知,相较于仅依靠惯性导航,无人车使用基于UKF的惯性磁感应定位方法具有更高的定位精度:全过程中x、y、z方向上的位置误差均小于0.75 m,有效地抑制了惯导的发散。
3 结论
针对卫星拒止条件下的室内导航问题,本文结合磁信标定位系统及MEMS惯性传感器提出了一种不受传感器姿态和磁信标磁矩影响的惯性磁感应定位方法,并通过实验与仿真结合的方式验证了方法的有效性。主要内容有:
1)在双轴人工磁信标磁场分布规律的基础上详细推导并建立了不受传感器姿态和磁信标磁矩影响的磁感应矢量夹角观测模型,通过实验验证了模型的有效性。
2)提出了一种基于UKF的惯性磁感应定位方法,实现了惯导数据与磁感应数据的融合。利用数值仿真的方式进行验证,结果表明,该方法能有效地抑制惯性导航的发散,适用于较高精度的室内导航定位。
本文的研究成果对惯性磁感应组合导航系统在室内场景下的应用具有较好的理论价值和实践价值,但受限于磁信标有效作用域的大小,目前该套系统的使用范围有限,后期可通过提高磁信标磁场覆盖范围和磁传感器精度的方式扩大惯性磁感应组合导航系统的使用范围。
