基于原始观测值的UWB增强GNSS精密单点定位方法研究

龙宸君, 吴宗洲, 申志恒

(武汉大学测绘学院, 武汉 430072)

0 引言

随着数字地球和智慧城市的迅速发展,人们对位置服务的需求越来越迫切[1],基于全球导航定位系统(global navigation satellite system,GNSS)的卫星定位技术得到了充分研究[2-4]。相比于差分形式的卫星定位技术,精密单点定位(precise point positioning, PPP)技术利用单台GNSS接收机伪距、载波相位观测值、高精度卫星轨道和钟差产品即可实现全球范围内的高精度定位[5],具有作业范围灵活、作业条件简单等优势。然而,由于计算能力的限制,PPP在实际应用中存在局限性,一方面,PPP需要数十分钟的收敛时间[6]来获得厘米级的定位精度,另一方面,复杂的卫星观测条件和不同精度的精密产品[7]也会导致PPP结果的重收敛。同时,在一些观测环境较复杂的地区,GNSS还存在信号强度低、容易失锁、观测不足、多路径效应严重[8]等问题。

针对PPP的上述挑战,采用UWB增强GNSS的方案,通过架设UWB基站提高PPP解的精度、缩短收敛时间。超宽带(ultra-wideband, UWB)定位技术是一种利用窄脉冲、在理论上达到厘米级精度的非载波通信技术[9],具有时间分辨率高、抗多径干扰能力强、安全性能优越等优点,广泛地用于测距、室内定位、多机器人协同等方面[10]。基于到达时间(time of arrival, TOA)的UWB定位原理与GNSS相似,都利用了测距信息,通过空间后方交会得到移动站的位置。而且UWB不存在相位模糊度[11],测距精度一般优于伪距。因此UWB具备潜在的GNSS增强性能。

目前利用UWB增强GNSS定位的研究中,CHIU[12]等提出在复杂的城市环境下进行UWB/GNSS紧组合定位并使用UWB距离测量值来增强GPS-RTK,但其在运动状态下只能达到米级的定位精度。周振南[13]等对北斗卫星导航系统和UWB松组合定位方法展开研究,利用扩展卡尔曼滤波器对定位误差状态进行最优估计,提高了系统从室外到室内定位的连续性与定位结果的可用性。MacGougen[14]等研究了用于精密定位的GPS/UWB紧组合模型,证实了浮点解可以达到亚米级精度、缩短了固定解的收敛时间。然而,探讨UWB增强PPP的研究资料非常稀缺,并且对于GNSS和UWB接收机的测量参考点的不一致性,大部分研究是通过相位中心高差、卫星的高度角和方位角[15]或者相关性函数[16]进行改正,而这会给获取GNSS框架下绝对坐标带来误差,因此本文聚焦于UWB增强PPP方法,同时顾及到系统成本等因素,进一步评估了UWB锚点数对系统定位性能的影响。

本文提出一种基于原始观测值层面UWB增强PPP的定位方法,首先阐述精密单点定位和UWB定位原理,通过姿态变换统一传感器参考点,实现观测值层面上的传感器紧密集成。根据实际采集的低成本传感器数据,通过解算比较验证了提出方法的可行性和有效性,并对比不同锚点数的效果,综合成本因素选取最佳锚点数,为本方法的工程实施应用提供了思路。

1 方法

1.1 精密单点定位原理

GNSS伪距和载波相位原始观测方程为

(1)

(2)

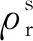
采用无电离层(ionosphere-free,IF)组合消除伪距和相位观测值的电离层延迟一阶项,对流层延迟误差中的湿延迟误差通过引入未知参数进行估计,干延迟误差通过Saastamoinen模型改正[17],其观测方程如下

(3)

(4)

卫星位置和卫星钟差通过精密卫星轨道和钟差产品获取,接收机位置、接收机钟差、无电离层组合模糊度、天顶方向对流层延迟参数和不同的卫星系统间存在的系统间偏差等未知参数的处理方法如表1所示。

表1 PPP参数处理策略

将表1的参数写成列矢量的形式如下

(5)

式中,δr表示接收机位置误差,δtr表示接收机钟差,ISB表示系统间偏差[18],zpd表示天顶方向对流层湿延迟,N表示模糊度。

考虑不同卫星星座观测值的差异,因此一般对不同星座采用不同的权比,具体数值由经验值确定。对于同一卫星系统内的卫星,由于观测噪声与卫星高度角有明显的相关性,一般采用与高度角相关噪声模型[19]。本文采用的高度角定权模型如下

σ2=a2+b2cos2θ

(6)

式中,θ为卫星高度角,a和b为常数,一般通过拟合或者经验值给定,对于观测值线性组合,可通过误差传播理论确定其方差。在式(6)以高度角为定权的基础上,再将载波相位和伪距的权比设为100∶1。

1.2 UWBTOA定位原理

UWB通过测量信号从定位标签(tag)发出到邻近锚点(anchor)的时间,即可获得标签到锚点天线的距离观测值,根据几何定位原理求得标签的位置。其观测方程如下

Ri,T=

(7)

式中,Ri,T表示标签到第i号锚点的距离观测值,(Xi,Yi,Zi)表示第i号锚点的坐标值,(XT,YT,ZT)表示标签的坐标值,ν表示距离观测值误差。将上式线性化后,得到式(8)

(8)

式中,δRi,T表示距离的观测值减去距离的计算值,δXT,δYT,δZT表示标签三维坐标误差,ρi,T表示标签到锚点的距离的计算值。将所有UWB锚点的观测方程集合成一个观测方程

δR=Vδr+v

(9)

式中,δR表示所有UWB锚点距离的观测值减去距离的计算值,V表示其对应的方向余弦矩阵集合,δr表示坐标误差,v表示每个锚点的距离观测值误差集合矢量。

UWB观测值采用接收信号强度(RSSI)进行定权,模型如下

(10)

式中,RSSI为当前UWB观测值的信号强度,σ0为经验测距误差。

1.3 PPP/UWB紧组合系统

由于实际安装时,UWB和GNSS天线相位中心无法保持完全一致(图1),需要将UWB和GNSS测量的参考点统一后进行解算。

图1 天线相位中心及杆臂示意图Fig.1 Sketch map of antenna phase center and arm lever

我们利用航姿参考系统(attitude and heading reference system,AHRS)提供载体的姿态信息,将RTK/INS的姿态解作为载体的姿态,通过测量的GNSS和UWB空间杆臂,将二者参考中心进行了统一[20],公式如下

(11)

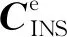
将式(11)作误差扰动分析,可得

(12)

(13)

式中,RUWB表示UWB距离的测量值,rAnchor表示锚点的位置。合并GNSS和UWB的观测信息形成紧组合系统,组合后的观测方程如下

(14)

(15)

基于扩展的卡尔曼滤波(extended Kalman filter, EKF),随机模型采用1.1和1.2节所述定权方法,合并式(13)和式(14)联合估计,即可实现基于原始GNSS和UWB观测值的紧组合。

2 实验验证

为验证UWB增强精密单点定位方法,对小推车在校园广场上采集的一组动态数据分别进行多系统PPP和UWB增强PPP,分析得到的定位结果。采集环境如图2所示,由于环境开阔,地面真值通过厘米级的RTK/INS解获取。使用的8个UWB锚点的分布及小车运行轨迹如图3所示。该算法的实现基于武汉大学测绘学院开发的GREAT(GNSS+REs-earch, application and teaching)软件。

图2 采集环境Fig.2 The environment of collection

图3 锚点分布与实验轨迹Fig.3 Anchor distribution and experimental trajectories

采集UWB的设备型号为Nooploop LinkTrack P-B,使用了如图3所示的8个锚点,测距残差如图4,从图中可以看出,大部分静态定位在±0.2 m,动态定位在±0.5 m。GNSS接收机型号为u-blox ZED-F9P,多GNSS天线型号为HT-3701B。为模拟验证实时应用中的性能,本文采用法国国家空间研究中心(Centre National D′Etudes Spatiales/National Centre for Space Studies, CNES)发布的实时存档GNSS精密产品[21]。移动小车的姿态信息使用RTK/INS解。

图4 UWB定位残差Fig.4 UWB positioning residuals

3 实验结果分析

3.1 数据质量分析

图5给出了采集数据的每个历元的可用双频观测值卫星数。由图5计算和分析可知,本次实验GPS、GAL(Galileo)、BDS平均可用卫星数分别为5.6,7.9,5.0颗。除了400～800 s和1 200～1 400 s这两段时间内3个系统卫星数均出现明显减少,其余时间段卫星数量上下波动幅度较小,较稳定。

图5 可用卫星数量Fig.5 Number of available satellites

将采集的不同卫星的观测值作周跳探测,结果如图6所示,红线即为发生周跳的历元。由图6可知,周跳发生的时段集中在400～800 s和1 100～1 300 s,并且在这两个时段,G4、G9、G11、G25、E11、E25卫星明显存在双频观测值缺失。

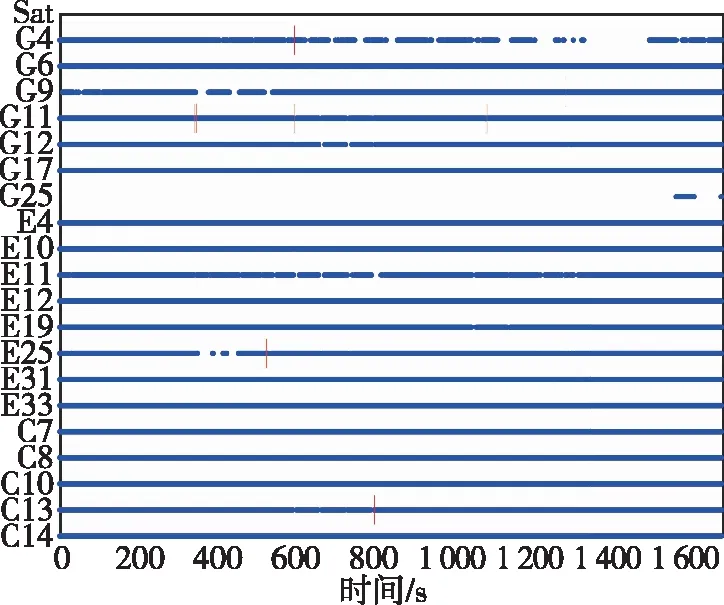
图6 卫星周跳探测Fig.6 Satellite cycleslip sdetection

综上所述,本次实验采集的数据整体质量较好,观测值较完善。卫星数从多到少依次为Galileo、GPS、BDS系统。在400～800 s时段和1 100～1 400 s 时段的数据质量较差,卫星数减少,观测值出现周跳。

3.2 UWB增强精密单点定位结果

双系统定位结果如图7所示,PPP和UWB增强PPP的结果在3个方向上均发生收敛,且数据未出现残缺。三系统定位结果如图8,也发生了收敛,定位结果更加稳定。相较于双系统,三系统的垂(U)向更加准确,在1 000 s后更加接近于0,收敛效果更好。从图中可以看出,两组结果的UWB增强PPP在初始阶段时能够快速地达到较高的精度水平,各个方向均完成了收敛,相较于PPP更加稳定,波动幅度更小。

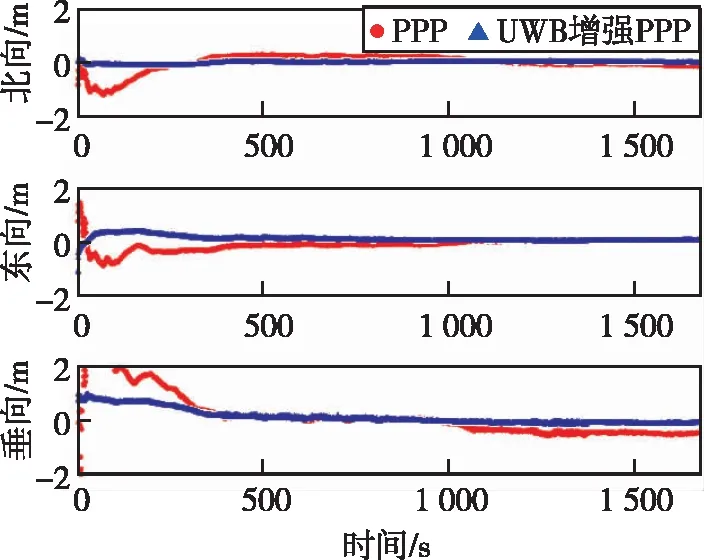
图7 双系统三方向误差(GPS/GAL)Fig.7 Error in three directions ofthe GPS/GAL system

图8 三系统三方向误差(GPS/GAL/BDS)Fig.8 Error in three directions of the GPS/GAL/BDS sytem

单GPS系统东向、北向、垂向误差如图9所示。由图可知,PPP和UWB增强PPP在600 s左右均出现重收敛现象,并且PPP结果的垂(U)向存在未收敛的情况,位置误差较大,东(E)和北(N)方向的定位精度在米级到分米级。

图9 单系统三方向误差(GPS)Fig.9 Error in three directions of GPS

由3.1可知,GPS平均可用卫星数5.6颗,且在600～800 s时段,G4、G11卫星观测值出现周跳,G4、G12、G25双频观测值出现缺失,卫星数在4～5颗。观测数据质量较差导致定位结果出现重收敛。尽管是观测数据质量较差的单系统,UWB增强PPP的解算结果相较于PPP也更加稳定,波动幅度也相对较小。

计算3个方向上误差值的均方根(RMS)作为评定精度的指标,并计算误差值的收敛时间。对于收敛时间的定义为3D定位误差从首历元开始,当某一历元的误差在0.3 m以内,并且此后连续5 min 的平均误差也均在0.3 m以内,则认为从首历元到该历元的时间为收敛时间。 RMS的计算公式如式(16)所示

(16)

计算单系统、双系统、三系统PPP和UWB增强PPP的RMS和收敛时间,得到结果如表2所示。

表2 三方向RMS值及收敛时间

单系统PPP的RMS值偏大,GPS可用卫星数不足,定位误差偏大,但通过UWB增强后,E、N、U 3个方向RMS值分别减少0.946,0.584,3.875 m。定位结果较好的双系统和三系统E,N,U方向RMS值通过UWB增强后,双系统从0.326,0.233,0.919 m分别下降到0.075,0.183,0.326 m,误差分别减少了0.251,0.050,0.593 m,分别改善了76.99%,21.46%,64.53%,三系统从0.287,0.258,0.848 m分别下降到0.087,0.162,0.328 m,误差分别减少了0.200,0.096,0.520 m,分别改善了69.69%,37.21%,61.32%。并且,单系统PPP存在不收敛的情况,经过UWB增强后开始收敛。双系统收敛时间从1037 s缩短到386 s,提升了62.78%,三系统收敛时间从748 s缩短到316 s,提升了57.75%。以上结果说明,UWB增强能有效提高PPP定位精度,缩短收敛时间。

3.3 锚点数量对结果影响

为降低系统成本并顾及UWB增强的性能,本节我们探究了锚点数(即几何构型)对PPP增强效果的影响。分别使用UWB增强双系统、三系统PPP定位,通过改变锚点数量(1/2/3/4/8),并按照表3选取锚点,得到3D位置误差分布函数(cumulative distribution function, CDF)如图10、图11。不同锚点数的3D定位误差的RMS和收敛时间如表4、表5所示。

表3 锚点选取

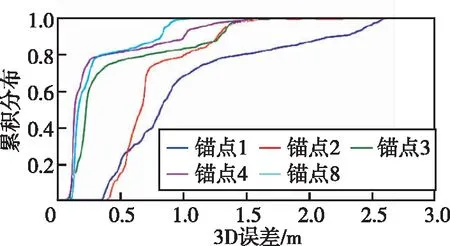
图10 双系统不同锚点数对定位结果的影响Fig.10 The influence of different anchor points on the positioning results of the GPS/GAL system

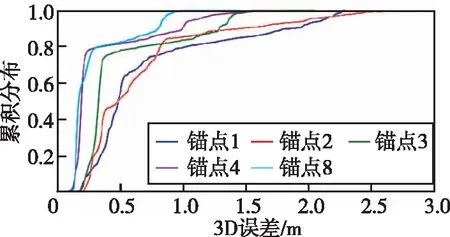
图11 三系统不同锚点数对定位结果的影响Fig.11 The influence of different anchor points on the positioning results of the GPS/GAL/BDS system

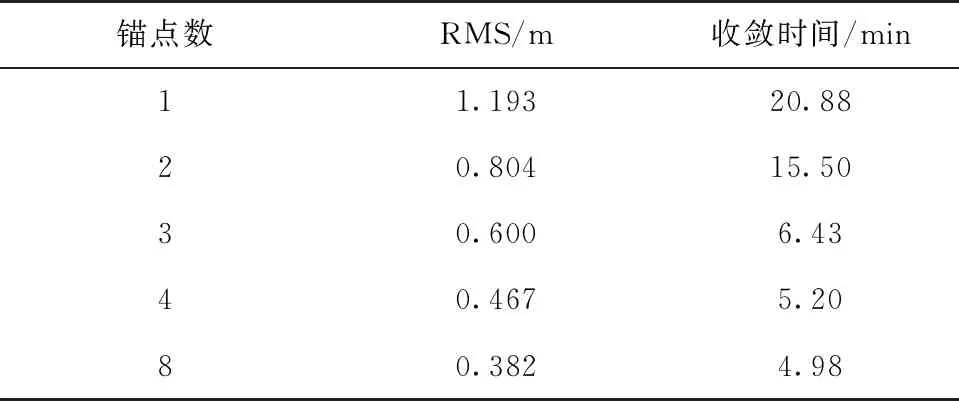
表4 不同锚点数增强双系统PPP的位置RMS与收敛时间

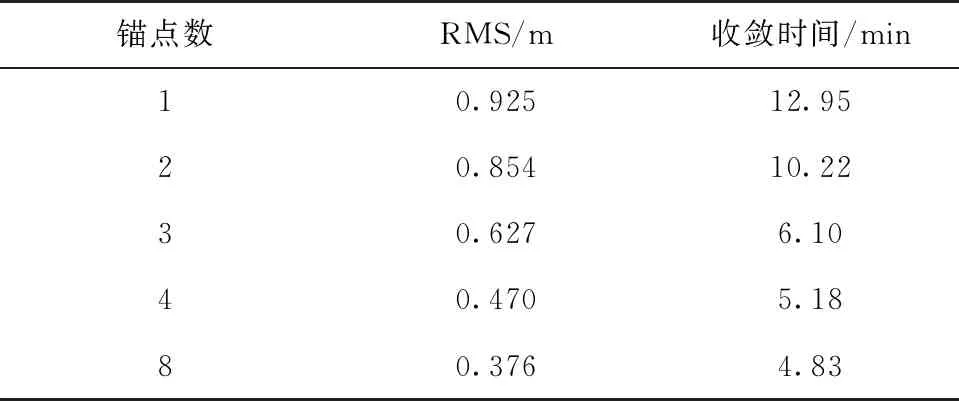
表5 不同锚点数增强三系统PPP的位置RMS与收敛时间

通过表4可知,双系统结果遵循锚点数越多,RMS值越小,收敛时间越短的规律。8锚点相较于单锚点,3D误差的RMS值减少了0.811 m,改善67.98%,收敛时间加快了15.9 min,提升76.14%。

且观察图10发现,当锚点数为3、4、8时,误差小于0.5 m的定位结果占比75%至80%,而当锚点数为1和2时占比只有10%至30%,说明当锚点数增加到3时,定位精度有明显提升。

由图11和表5可知,三系统结果也遵循锚点数越多,RMS值越小,收敛时间越短的规律。8锚点相较于单锚点,3D误差的RMS值减少了0.549 m,改善59.35%,收敛时间缩短了8.12 min,提升62.68%。当锚点数为3、4、8时,误差小于0.5m的定位结果占比75%至80%,当锚点数为1和2时占比50%,综合双系统定位结果可知,当锚点数为1和2时,没有较强的几何构形,UWB增强PPP方法的精度和收敛时间主要取决于PPP,只有锚点数至少为3,有较强的几何构型时,才能使结果明显增强。

根据双系统和三系统的定位结果分析可知,随着锚点数增多,RMS值变小,收敛时间变短,说明锚点数增多能提高定位精度,并且3锚点增强效果明显提升。对双系统而言,从3锚点到4锚点,RMS值下降0.133 m,改善22.17%,收敛时间加快了1.18 min,提升19.17%。8锚点相较于4锚点,锚点数增加到2倍,RMS值只减小了18.20%,收敛时间只加快了4.17%,所以考虑到系统成本,双系统推荐采用4锚点UWB增强;同理,对三系统而言,从3锚点到4锚点,RMS值减小了0.157 m,改善25.04%,收敛时间加快了0.92 min,提升15.03%,从4锚点到8锚点,RMS值减小了0.094 m,改善20%,收敛时间加快了0.35 min,提升6.75%,锚点数增加1倍,提升同样不明显。综上,对于低成本接收机而言,仅采用4个锚点即可实现明显的增强效果。

4 结论

提出了主要应用于小范围场景的UWB增强PPP高精度定位的方法,通过实际采集的数据,比较了精密单点定位和UWB增强的精密单点定位的结果,验证了提出的方法能够有效提高PPP的收敛效率和定位精度。考虑到搭建UWB基站等额外基础设施需要一定的成本,也对锚点数对定位结果的影响展开了探讨,得出的结果如下:

1)UWB增强的精密单点定位技术定位精度更高。RMS的值相比于PPP更小,单系统、双系统和三系统每个方向RMS值平均减少了1.802、0.298、0.272 m;收敛时间比PPP更短、收敛效果更好。由于可用卫星数过少导致PPP不收敛的单系统,经增强后在1 096 s发生收敛,双系统收敛时间加快了651 s,三系统收敛加快了432 s。

2)更多的锚点数量会增强锚点的几何构型,从而提高UWB增强精密单点定位精度,缩短收敛时间。锚点数从1到8,双系统和三系统的3D误差的RMS分别减少了0.811和0.549 m,收敛时间加快了15.9 min和8.12 min。充分考虑系统成本、锚点数增加对于定位精度和收敛时间的提升,认为对于支持多个系统的低成本GNSS接收机来说,采用4个几何构形较好的UWB锚点进行UWB增强PPP方法就有明显的效果。