基于白鲨优化极限学习机的三维力传感器非线性解耦

孙世政， 庞珂， 于竞童， 陈仁祥

（重庆交通大学 机电与车辆工程学院，重庆 400074）

1 引 言

多维力传感器广泛应用于机械设备、生物医疗、碰撞检测、机器人等领域［1-6］，具有结构简单、体积小、重量轻等特点［7-8］，能有效实现交互力测量反馈。在实际工程应用中，由于环境温度、实际工况等因素，各维度间存在耦合干扰，传感器不可避免地出现测量精度损失问题，因此需探索出一种高效、精准的解耦方法解决传感器的精度损失问题。

针对多维传感器的维间耦合问题，目前降低维间耦合的方法有结构解耦和算法解耦。结构解耦方面，国内外学者设计了十字梁结构［9］、Y型横梁［10］、轮辐式结构［11］等经典弹性体结构，张海霞等人［12］设计一种将矩形截面梁转变为应变梁的传感器，使自身结构具有解耦功能，该传感器测量精度高，维间耦合干扰小，因受传感器制造、安装影响，其消除耦合能力有限；Long等人［13］提出了一种基于FBG新型超薄三维力传感器，该传感器利用浮动梁嵌套弹性体结构，有效测量三维力，由于测量结构存在力感知不均衡，其力与力间存在耦合干扰。上述结构解耦方法均存在维间耦合干扰，对制造和安装精度要求较高。

算法解耦方面，国内外学者通过线性解耦［14-16］与非线性解耦［17-20］消除维间耦合干扰。最小二乘法（Least Sqaure method， LS）为常见线性解耦方法，彭小武等人［14］利用最小二乘法对十字梁型三维力传感器进行拟合标定，解耦结果I类误差控制在2.36%范围内，II类误差最大值达到2.1%，由于消除非线性耦合能力较差，其解耦能力有限；韩康等人［16］提出了高灵敏度六维力传感器并建立最小二乘法线性标定的解耦模型，实验表明三个方向解耦后残余耦合误差小于1.2%，由于需补偿非线性耦合，其解耦效率较低。上述线性解耦方法均存在解耦效率低，消除非线性耦合能力差等问题。

目前国内外学者主要基于误差反向传播（Back Propagation， BP）神经网络、粒子群优化（Particle Swarm Optimization， PSO）、极限学习机（Extreme Learning Machine， ELM）等算法以构建非线性神经网络，达到消除维间非线性耦合目的。Li等人［17］设计了一种基于FBG的紧凑型三维力传感器，采用基于线性整流函数（Rectified Linear Unit， ReLU）的BP神经网络方法解耦。该方法相较于LM和BP算法，能显著提高传感器精度，因在三个方向都存在较大的误差突变点，容易导致过拟合问题。李映君等人［18］为解决六维力传感器维间耦合问题，利用基于径向基函数（Radial Basis Function， RBF）神经网络解耦，I类误差最大达到1.29%，II类误差最大达到1.56%，但RBF神经网络算法参数较复杂。Yao等人［19］将ELM和PSO相结合，采用PSO-ELM算法对基于FBG的三维力传感器进行非线性解耦，降低传感器水平方向维间耦合干扰，轴向耦合误差达到5.70%，解耦能力有限。

为解决上述问题，本文提出一种基于FBG的一体式低耦合三维力传感器，具有结构简单、制造成本低、体积小等优点，并基于此提出基于白鲨优化极限学习机解耦算法。结构解耦方面，利用FBG传感原理，布设4根FBG，所设计的分层弹性体结构可以减小各方向的交叉耦合；算法解耦方面，利用白鲨优化算法对极限学习机神经网络随机产生的输入权值与隐含层阈值进行优化计算，并获取最优参数组合，建立WSO-ELM神经网络模型，验证了WSO-ELM算法对所设计三维力传感器的非线性解耦的可行性。实验结果表明，该方法具有较好的解耦效果，可以有效降低传感器的耦合误差。

2 传感原理与结构设计

2.1 传感原理

由耦合模理论［21］可知，光源发出的宽带光在光纤布拉格光栅上发生反射和透射，满足布拉格反射条件的光被反射，反之被透射，其传感原理图如图1所示。

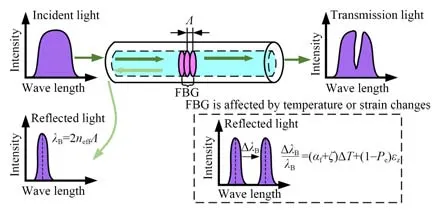
图1 光纤光栅传感原理图Fig.1 Schematic diagram of fiber Grating sensing

反射光的中心波长λB为：

其中：neff为光栅纤芯有效折射率，Λ为光栅周期。λB受轴向应变εz和温度变化ΔT影响时会发生漂移：

其中：Pe弹光系数，αf为热膨胀系数，ζ为热光系数。

2.2 传感器结构设计

如图2所示，该传感器主要由传力柱、上盖、侧盖、弹性体结构和底盖组成。传力柱顶端设有螺纹，用于连接机器人末端执行器，便于力传递；盖与侧盖组成传感器的外壳体，侧盖设有FBG输出通道的出口孔；底盖设有四个螺纹孔，用于连接机器人关节。

图2 传感器结构示意图Fig.2 Schematic diagram of sensor structure

如图3（a）所示，弹性体结构可分为三层，从上到下分别为经典十字梁测量层、测量柱层和固定层。十字梁测量层为4根弹性横梁；测量柱层为4根弹性竖梁；固定层为圆盘结构的底盘。4根弹性横梁位于同一平面，两两相互垂直，每根横梁长度、宽度和厚度分别为16 mm，5 mm和4 mm。4根弹性竖梁以90°间隔围绕中心均匀分布，上端与传感器外圆环连接，下端与底盘表面连接。每根弹性竖梁设有上下两个开口方向相隔90°的通槽，以增强传感器灵敏度，其尺寸为长6 mm，宽3 mm，高4 mm及长7 mm，宽2 mm，高6 mm。底盘设有螺纹孔，用于连接传感器底盖及机器人关节。

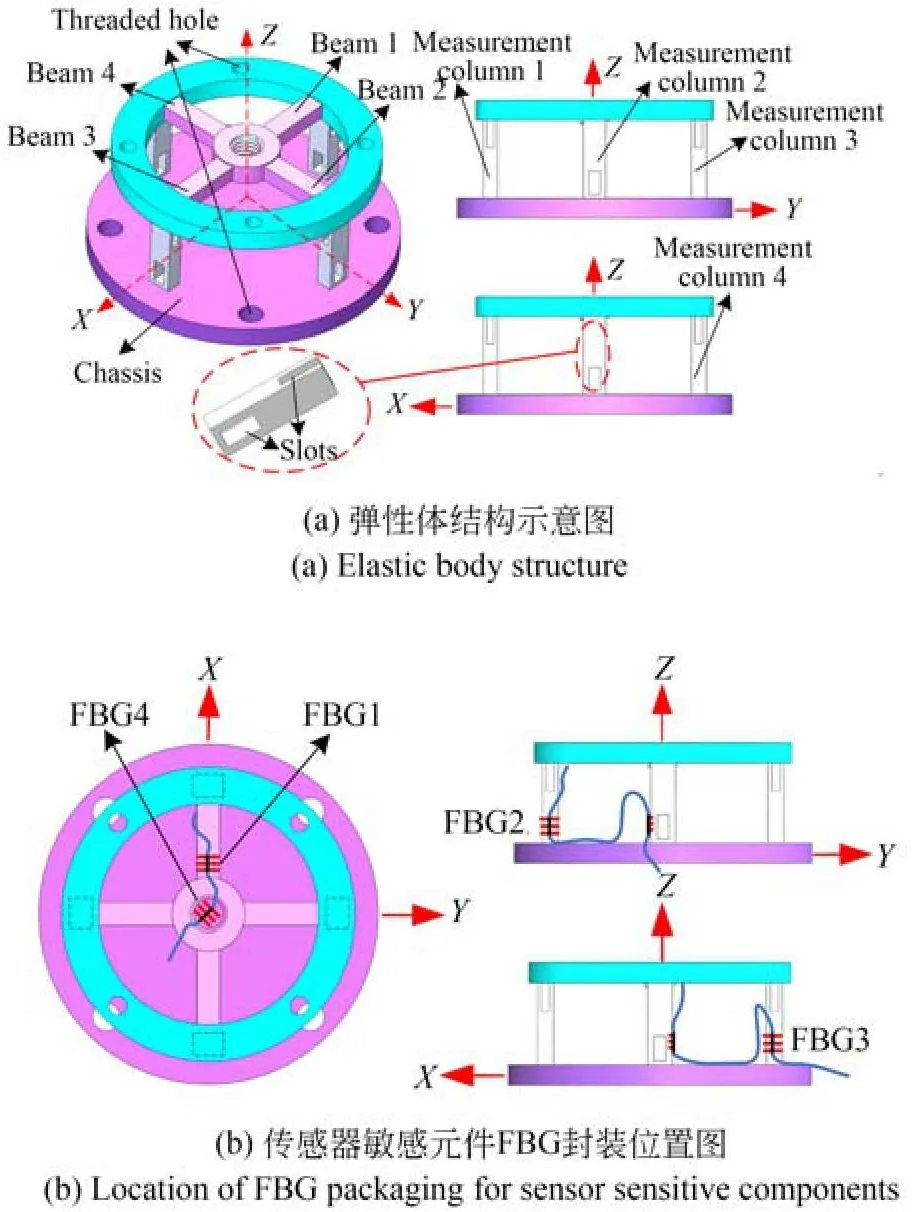
图3 弹性体结构图Fig.3 Sensor structure diagram

如图3（b）所示，以底盘中心点为坐标原点O，以两个相邻水平弹性梁的中心线为X，Y，建立笛卡尔坐标系。将4根FBG粘贴于弹性体应变敏感区域，FBG1位于XOY平面，并封装于X方向的十字梁处并靠近中心，以测量轴向力Fz。FBG2，FBG3分别位于YOZ平面、XOZ平面，并封装于两根正交测量柱处靠近底盘处，以测量一对水平方向的正交力（Fx，Fy）。FBG4封装于底盘中心处，作为温度补偿。

3 三维力耦合实验与分析

3.1 耦合实验

三维力传感器实物图及标定实验系统如图4所示，并通过标定实验，获得大量三维力传感器在受力状态下的数据样本。

图4 标定实验系统Fig.4 Calibration experimental system

该传感器标定系统主要由FBG传感器、力加载系统和解调系统组成。力加载系统采用“牵引丝-砝码”悬浮加载，简单稳定。其中，用于加卸载的标准砝码精度达到M1级。牵引丝绳直径为0.6 mm，最大载荷为25.3 kg（重力加速度约为10 m/s2）。解调系统采用美国MOI公司开发的FBG波长解调仪（解调精度：1 pm，波长范围：1 460~1 620 nm，采样频率：1 kHz），以实现FBG中心波长的解调。

首先，将FBG传感器处于未加载状态，静置五分钟，并用解调系统记录每根FBG的中心波长，为初始中心波长，其中，FBG1，FBG2，FBG3的初始中心波长分别为1 544.178 nm，1 539.435 nm，1 539.103 nm；然后，在0~100 N之间每隔10 N分别向每个方向施加载荷。每个方向的载荷均从最小值增加到最大值，再从最大值减少到最小值。该加载卸载实验重复三次，并通过解调系统记录下每次加载卸载的FBG中心波长。实验最终数据取这三次实验的FBG中心波长漂移量的平均值，一共180组数据。

3.2 耦合分析

将180组标定原始数据进行整理，可以得到传感器耦合干扰图，如图5所示。

由图5可知，施加某一方向力时，三维力传感器其他输出通道的FBG中心波长漂移量受到干扰变化，呈非线性，从而影响传感器测量精度。施加Fx对z方向的耦合干扰最大，FBG中心波长最大漂移量达到21.05 pm。Fx对y，z方向的最大漂移量分别为14.47 pm和21.05 pm，Fy对x，z方向的最大漂移量分别为13.82 pm和18.41 pm，Fz对x，y方向的最大漂移量分别为10.29 pm和7.76 pm。

实验结果表明，该三维力传感器结构施加轴向Fz时，对x，y方向的耦合干扰较低，测量精度较高，但由于结构一体化，该传感器轴向受水平方向正交力（Fx，Fy）的耦合干扰较大，同时Fx，Fy之间存在着较大的耦合干扰，呈非线性关系，所以仍需通过算法对此进行非线性解耦以降低耦合干扰。

4 非线性解耦理论

4.1 极限学习机理论

极限学习机是一种单隐层前馈神经网络学习算法，具有很好的非线性拟合能力［22-23］。该算法通过对单隐层前馈神经网络的输入权值w及隐含层阈值b进行动态选择，同时对输出权值β的解析确定，以求得最优解。ELM神经网络结构如图6所示。

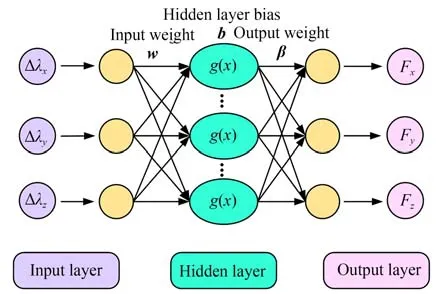
图6 极限学习机神经网络结构图Fig.6 Structure diagram of extreme learning machine neural network

设有N个任意样本，该ELM神经网络结构输入3根FBG的中心波长漂移量Δλn×3，输入层与隐含层的输入权值矩阵为w3×s，隐含层与输出层的输出权值矩阵为βs×3，隐含层阈值为b，最终输出x，y，z维度的受力值为Fn×3。其可表示为：

其中：Hn×s为隐含层输出矩阵，βs×3为输出权值矩阵。Hn×s可表示为：

其中：ws·Δλn为ws和Δλn内积，ws为连接第s个隐含层神经元与输入层神经元之间的权值，Δλn为第n个FBG中心波长漂移量的输入，bs为第s个隐含层阈值，g（x）为非线性分段连续激活函数，即Sigmoid函数，其可表示为：

由式（3）、式（4）可得：

4.2 白鲨优化算法［24］

白鲨优化算法是一种模仿大白鲨导航和觅食行为的新型智能优化算法，具有连续稳定搜索、高效实现全局最优解的特点。

白鲨优化算法主要包含四个阶段：快速向猎物移动；向最佳猎物移动；向最佳进攻位置靠近；鱼群行为。白鲨利用其听觉和嗅觉等感官，根据猎物移动时，感受波浪的停顿从而感知猎物的位置，并快速向猎物移动，朝猎物移动速度可表示为：

其中：i为种群大小，k为迭代次数，μ为收缩因子，为第i条白鲨在第（k+1）次迭代速度，vik为第i条白鲨在第k次迭代速度，wgbestk为白鲨在第k次迭代全局最佳位置，wik为第i条白鲨在第k次迭代位置，为群体已知最佳位置，p1，p2为wgbestk和对wik的影响参数，c1，c2为［0，1］内生成的随机数以增强算法搜索能力避免陷入局部最优解，实现全局最优解。其中，

式中：τ为加速度系数。

继续导航寻找猎物，重新更新位置，并向最佳猎物移动，其更新位置为：

其中：l，u为搜索空间上下限，a，b为一元二次向量，wo为逻辑向量，f为波浪运动频率，r，rand为［0，1］内的生成的随机数。其中，

式中mv表示白鲨靠近猎物时，随着迭代次数增加的运动力，其可表示为：

式中：a0和a1为常数。

当白鲨发现猎物，围攻猎物以后，就向其最佳进攻位置靠近进行捕杀猎物：

其中：w′ik+1为第i条白鲨相对猎物位置的更新位置，sgn（r2-0.5）通过设置1或-1来改变搜索方向为猎物与白鲨之间的距离，ss为白鲨嗅觉与视觉强度。其中，

式中，a2为常数。

进一步模拟白鲨群行为，保留前两个最优解，并根据最优解更新其他白鲨位置，即为鱼群行为，可表示为：

通过最佳白鲨进攻位置和鱼群行为，可以确定WSO的集体行为，扩大了勘探、开发的范围。

4.3 基于白鲨优化极限学习机算法

基于白鲨优化极限学习机是一种将WSO与ELM相结合的改进算法，通过WSO搜索最佳输

其中：N为样本总数量，ni为第i个样本的预测输出值，mi为第i个样本的真实输出值。

算法实现过程如图7所示：

图7 算法流程图Fig.7 Algorithm flow chart

Step1 将实验中所获得的180组数据随机选取150组数据为训练集，30组数据为测试集，并分别组成为150×6，30×6的两个向量矩阵，并进行归一化处理；

Step2 对WSO参数进行初始化并设置ELM网络参数；

Step3 确定WSO-ELM种群数目，通过式（18）计算出种群个体适应度（即MSE），并根据所得适应度值利用WSO-ELM寻找种群最优个体位置（即MSE最小的个体位置）；

Step4 由式（7）到式（16）更新WSO中的个位移动速度、向最佳猎物移动位置、最佳进攻位置、其余个体位置，以寻找最优个体位置;

Step5 通过训练集对ELM神经网络模型进行训练，并计算出最小的个体适应值；

Step6 判断训练所得最小适应值是否满足终止条件，若满足则输出最小适应值，并获取ELM的最优权值和阈值，计算出β矩阵、H矩阵；反之，入权值w和隐含层阈值b，避免极限学习机的随机性。该算法通过不断更新输入权值和阈值，最终使预测数据与真实数据的均方误差（Mean Square Error， MSE）达到最小，采用如下表达式计算：返回执行Step4；

Step7 通过计算出的β矩阵、H矩阵进行ELM网络仿真测试；

Step8 利用Step7所构建的ELM神经网络模型对测试集数据进行预测，获得预测的传感器三维的力输出值。

5 非线性解耦实验

将标定实验所得三个方向不同加载力的FBG中心波长漂移量及加载力的数据集先进行归一化处理，然后随机划分为训练集、测试集以训练神经网络模型精度并预测，导入WSOELM神经网络中作为输入值，其输出值为三个维度的加载力。WSO-ELM神经网络中的ELM神经网络模型的输入层为三个方向不同加载力的FBG中心波长漂移量及加载力，输出层为三个维度的加载力，隐含层神经元初始个数为7。WSO-ELM神经网络中WSO的种群数量为100，加速度系数τ为4.11，白鲨初始速度pmin为0.5，从属速度pmax为1.5，波浪运动最小频率fmin为0.07，最大频率fmax为0.75，a0为6.25，a1为100，a2为0.000 5。在WSO-ELM神经网络模型中，隐含层神经元个数的选择至关重要，影响着预测值MSE和解耦时间。预测值MSE和解耦时间的参数组合则决定了网络模型的解耦精度和效率。

5.1 算法参数的选取

以训练集训练网络模型的精度后，最终确定隐含层神经元个数范围在7~35内解耦精度和效率达到最好。通过测试集在ELM处于不同隐含层神经元个数时，寻求MSE、解耦预测时间的最佳参数组合。

由图8可得，隐含层神经元个数大于13时，随着隐含层神经元数的增加，均方误差、解耦预测时间平稳下降，并达到一个最低值，然后持续缓慢上升。隐含层神经元个数为20时解耦预测时间最短，为0.006 s，相应的MSE取得了0.21；隐含层神经元个数为25时，MSE取得最小值0.18，相应的解耦预测时间为0.014 s。为保证解耦精度的同时，具有较高的解耦效率，隐含层神经元数应取25，使WSO-ELM神经网络模型具有较好的解耦效果。

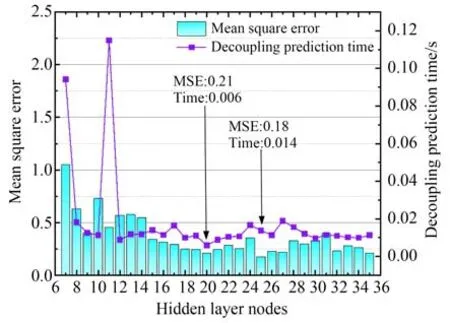
图8 MSE与解耦预测时间关系图Fig.8 Relationship between MSE and decoupling time

5.2 实验结果

WSO-ELM神经网络模型训练预测完成后，如图9所示，拟合直线表示三维力传感器的实际加载力与解耦输出力之间的线性关系。从图中可以知道，三维力传感器的的实际加载力与解耦输出力的线性拟合良好。x方向的线性拟合优度R2达到0.999 93，y方向的线性拟合R2达到0.999 76，z方向的线性拟合R2达到0.999 94。该结果表明，采用WSO-ELM算法进行解耦处理后，该三维力传感器具有良好的线性度，有效地验证了WSO-ELM算法对该三维力传感器的非线性解耦的可行性。

图9 各方向解耦后的线性特性Fig.9 Linear characteristics after decoupling in three directions

从图10中可以看出，仅施加某一单维力时，WSO-ELM算法对x，y，z方向的耦合干扰有着明显的解耦效果。传感器仅施加x方向力时，x，y，z方向最大耦合干扰未解耦前分别为88.13 N，4.11 N，11.03 N，解耦后分别为99.35 N，0.54 N，0.26 N，x方向提高12.73%，y，z方向降低86.86%，97.64%；仅施加y方向力时，x，y，z方向最大耦合力干扰未解耦前分别为5.23 N，87.33 N，7.24 N，解耦后分别为0.82 N，100.68 N，0.77 N，y方向提高15.29%，x，z方向降低84.32%，89.36%；仅施加z方向力时，x，y，z方向最大耦合干扰未解耦前分别为2.92 N，2.20 N，99.08 N，解耦后分别为0.81 N，0.89 N，99.89 N，z方向提高0.82%，x，y方向降低72.26%，59.55%。实验结果可以表明，WSOELM算法对所设计三维力传感器的非线性解耦的有效性、可行性。

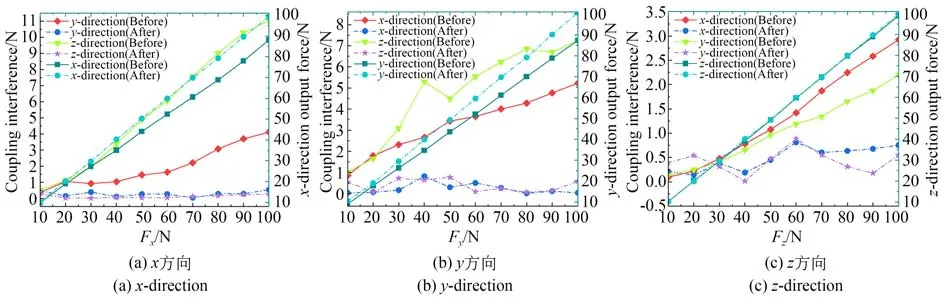
图10 各方向解耦后的耦合误差输出Fig.10 Coupling error output after decoupling in three directions

5.3 解耦误差评定

多维力传感器在各种解耦算法中的一个重要评定指标是平均I类误差和平均II类误差［25］。通过分析平均I类误差和平均II类误差可以阐明多维力传感器测量精度的高低，同时可以验证算法解耦效果的有效性、准确性。平均I类误差是各方向测量结果的平均值与实际加载的偏差程度，即平均I类误差，其计算公式可表示为：

其中：为i方向测量结果平均值与实际加载的偏差，yi为i方向满量程值。

由于多维力传感器具有多个通道，各个方向的输出通道之间存在着维间耦合干扰程度，即平均II类误差，其计算公式可表示为：

其中，，分别为仅在其余两方向施加单维力时，i方向的平均耦合干扰值。

通过比较平均I类误差、平均II类误差的大小，可以对解耦算法的效果进行评定。将WSOELM与ELM，BP，LS的各方向的平均I类误差、平均II类误差进行对比，如图11所示。

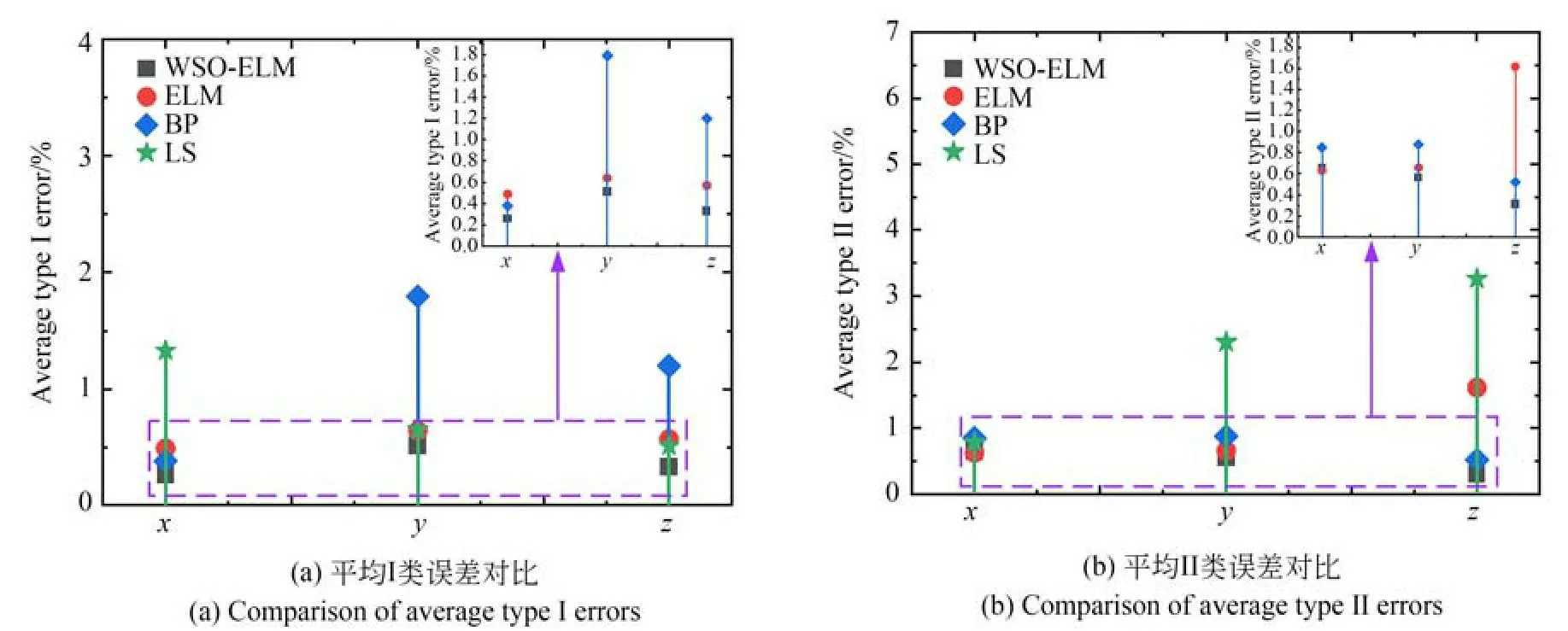
图11 各类算法误差对比Fig.11 Comparison of four algorithm errors

相较于非线性解耦算法，线性解耦算法LS整体平均误差较高，其中平均I类误差为1.33%，0.65%，0.51%，平均II类误差为0.79%，2.31%，3.26%；WSO-ELM算法各方向的平均I类误差最低，x，y，z三个方向平均I类误差分别为0.26%，0.51%，0.33%；ELM算法x方向平均II类误差最低，达到0.63%；WSO-ELM算法y，z方向平均II类误差最低，分别为0.56%，0.31%。对于解耦效率，BP算法解耦时间较高，达到0.338 s，ELM算法解耦时间较低，达到0.010 s，WSO-ELM算法解耦时间达到0.014 s。综上，相较于LS，ELM，BP算法，WSO-ELM算法稳定，误差集中，更具有良好的非线性解耦性能。其对比结果如表1所示。

表1 各类算法解耦精度与效率对比Tab.1 Comparison of decoupling accuracy and efficiency of four algorithms

6 结 论

针对三维力传感器维间耦合严重的问题，本文提出一种基于白鲨优化极限学习机（WSO-ELM）解耦方法。该方法在ELM神经网络的基础上，通过WSO算法全面稳定寻找最小适应值，确定ELM最佳参数组合，寻找均方误差和解耦时间的最佳参数组合。WSOELM是一种非线性解耦算法，其良好的解耦性已在文中得到验证。实验结果表明，该传感器解耦后最大平均I类误差达到0.51%，最大平均II类误差达到0.65%，传感测量精度显著提高，具有良好的非线性解耦能力，能够满足实际应用的需求。