基于Isard法的充电站服务范围划分与实时定价策略
2023-09-27吴佳龙蔡晔唐夏菲曹一家陈仲伟
吴佳龙,蔡晔,唐夏菲,曹一家,陈仲伟
(1.长沙理工大学电气与信息工程学院,长沙市 410114;2. 能源互联网供需运营湖南省重点实验室(国网湖南省电力有限公司经济技术研究院),长沙市 410004)
0 引 言
自2020年下半年以来,中国新能源汽车市场一直保持高速增长。充电设施是维系电动汽车运行的能源补给基础,根据中国电动汽车充电基础设施促进联盟(EVCIPA)发布的数据:2022年1到12月,充电基础设施增量为259.3万台,其中公共充电桩增量同比上涨91.6%,随车配建私人充电桩增量持续上升,同比上升225.5%[1-2]。而电动汽车用户的充电习惯与电动汽车充电价格息息相关[3],因此,提出合理的充电设施建设与定价指导方案,对于持续推进充电基础设施的建设[4-5]、减少新能源波动带来的影响[6-8]至关重要。
中国充电站行业处于快速增长期[9-11],研究充电站服务范围对于运营商们分析市场情况具有重要意义。服务范围是充电站市场竞争力的具象化结果[12-13],目前,国内外缺乏对于充电设施服务范围的研究,对于设施服务范围的研究大多以机场[14-15]、物流园区[16-17]、城市经济区[18-19]等作为研究对象。结合可达性原理、克鲁格曼指数等指标修正引力模型,采用规则化圆形展现服务范围,或者基于加权Vonoroi图提出充电站规划方法[20-21]。这类方法为研究充电站服务范围提供了思路,然而,多个充电站之间必然存在市场竞争关系,站与站之间的竞争会造成市场分布不均匀,充电站服务范围必然会呈现不规则化。虽然加权Vonoroi图方法优化了服务范围多边化的问题,但只能在固定范围内进行市场区域的划分,Isard法能够平等地看待各个充电站,强调了谁在主导。
充电站运营商制定的实时电价是影响自身服务范围的核心因素。合理的充电定价策略需达到4个目标,即:引导电动汽车用户有序充电[22-23],提升运营商的利润[24-25],提高充电桩的利用率,减小负荷峰谷差[26]。对于定价策略的研究,传统零售商或者运营商对电价的制定,大多是从需求侧入手,基于价格弹性矩阵调度需求侧响应,制定分时电价[27-28];也有学者考虑到零售商在制定电价套餐时用户的意愿与选择,通过对用户用电行为的分析,提出定价优化模型[29-30]。但以上文献都没有考虑到动态电价的变化对于零售商或者运营商自身市场划分的影响,缺乏对于动态服务范围的分析。本文在考虑充电站自身利润与电网辅助服务的基础上制定动态电价策略,从实际场景上分析电价与充电站服务范围的关系,为零售商或者运营商提供合理的定价建议。
综上所述,刻画充电站充电电价与服务范围的相互影响,对于提升充电站效益与促进充电设施建设具有重要意义。为此,本文通过场强变化动态刻画多主体市场竞争交互关系,通过考虑运营商收益与功率偏差的多目标优化来制定实时电价,为充电站的规划建设提供理论依据。
1 充电站服务范围的场强模型
1.1 充电站服务范围定义
二维空间中的一个设施或者一个企业,会对于它自身周围一定范围内的用户产生吸引力,当用户有需求时会选择去该设施或企业满足自身所需。充电站服务范围表示以充电站作为一个提供充电服务的中心时周围接受服务的电动汽车用户在地域空间上的分布范围,呈现不规则形状,如图1所示。图1中充电站i与充电站j同时对电动汽车用户a、b、c产生吸引力,虚线表示充电站散发出的服务范围场强,两种颜色表示两个充电站各自服务范围。
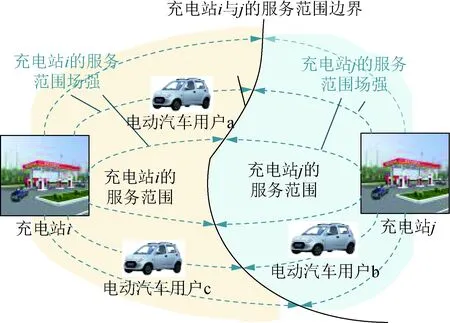
图1 充电站服务范围示意图Fig.1 Charging station service area diagram
充电站对于周围区域的吸引力不会突变,与点电荷产生的静电场类似,具有典型的无旋有散度场特点。根据亥姆霍兹定理得知,无旋有散度场的函数与距离矢量R2成反比。因此类比点电荷电场强,定义充电站服务范围场强为充电站对周围充电需求区域的吸引强弱。
如果对某地区进行一定精度的栅格划分,得到M个小网格区域,并定义为充电需求区域。任意一个充电站n都会对需求区域产生吸引力,从而产生服务范围,这个服务范围受周围充电站以及自身参数限制。根据Isard提出的“最强占领法”:如果发现充电站n对需求区域k的服务范围场强En.k,比其他充电站m对需求区域k的服务范围场强Em.k都大,则识别需求区域k为充电站n的服务范围,如式(1)所示:
Sn={S|En.k≥Em.k,m=1,…,N(m≠n)}
(1)
式中:Sn表示充电站n的服务范围;S代表充电站的服务范围划分依据;N为充电站总数。将需求区域k定义为市场需求区域,即式(1)表示在所有充电站中,充电站n对需求区域k的吸引力最大,则将需求区域k划分为充电站n的服务范围。
1.2 基于熵权法的充电站综合实力评价指标体系
充电站服务范围大小与自身综合实力息息相关。评价充电站的综合实力Cn的评价指标体系如图2所示,主要包括:充电站的合同容量、充电站快充桩数、慢充桩数、服务费、充电价格等。
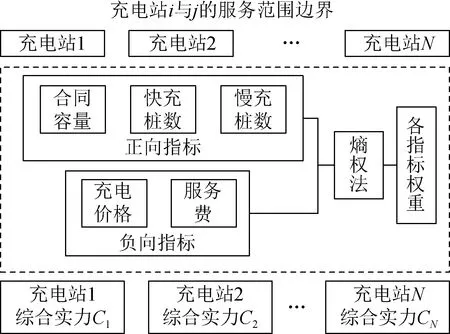
图2 充电站综合实力评价指标体系Fig.2 Charging station evaluation index system
图2中,合同容量、快充桩数、慢充桩数等均为正向影响因素,这些因素的数值越高,充电站的综合实力Cn越强,对周围需求区域的吸引力越强,用户更愿意去充电站n进行充电,服务范围Sn越大。充电价格、服务费等均为负向影响因素,其值越大,充电站服务范围越小。
依据熵值法对充电站的评价指标进行处理,得到充电站各指标的权重γ=(γ1,γ2,…,γI)。量化计算充电站n的综合实力,如式(2)所示:
(2)
式中:γi为第i个指标的权重;ci为相关系数,若γi为正相关评价指标则ci=1,若γi为负相关指标则ci=-1;Tn.i为第i项指标原始数值;Tmax.i为第i项指标最大值。
1.3 充电站的服务范围场强模型
类比点电荷场强公式,考虑平均距离与综合实力,计算充电站n对于充电需求区域k的服务范围场强大小,建立以充电站为中心的服务范围场强En.k,如式(3)所示。
(3)
式中:kc表示服务常量;rn.k为充电站n与需求区域k之间的距离,可通过经纬度计算。
根据Wilson模型[31],充电站n对充电区域k的充电服务能力如式(4)所示:
Tn.k=KCnDke-βrn.k
(4)
式中:Tn.k为充电站n对充电区域k的充电服务能力;K为归一化因子,描述充电站地域差异性,若忽略充电站n位置与需求区域k两地的区域差异,则令K=1;Dk为充电区域k的负荷需求量;β为衰减因子,决定了服务衰减速度的快慢。
结合静电力常量量纲,假设每个充电站服务常量相同,可推出kc如下所示:
(5)
(6)
式中:Cave为所有充电站的平均综合实力;Dave为所有需求区域的平均需求量;rave为充电站与需求区域的平均距离;tmax表示利用社会科学统计软件包(statistical package for the social sciences,SPSS)计算因子分析后综合得分大于0的充电站个数;Save_n表示全部充电站所在地区的平均面积。
2 基于充电站服务范围的充电需求

(7)
充电站n在t时刻的充电需求qn.t受自身充电价格Pn.t、其他充电站m的价格Pm.t共同影响,如式(8)所示。其中,充电需求qn.t是关于自身价格Pn.t的负相关函数,t时刻随着充电价格Pn.t的上升,充电站n的充电需求qn.t随之减少,并转移至该区域内其他充电站qm.t,导致充电站n的服务范围减小,其他充电站m的服务范围增大。
(8)

将充电需求qn.t与风光出力均转换成标幺值,如式(9)所示:
(9)

充电站一天内的收入En如式(10)所示:
(10)

为了验证模型存在最优解,对式(10)进一步计算,对模型求关于Pn.t与Pm.t的混合偏导数,可以证明得到:
(11)
基于此可以得知模型拥有且存在唯一的纳什均衡解,任意一个电动汽车充电站运营商n的收入由式(10)可以看出是一个关于充电价格Pn.t的二次函数,由于Pn.t二次项系数为负数,所以收入模型为凹函数且开口朝下。根据二次函数的性质可知,充电站收入函数有且存在唯一的最大值点,因此模型存在最优解。
3 基于服务范围的实时定价优化模型
当完全竞争的市场上有N家规模不同的充电站,且N家充电站分属H家不同的运营商,且H≤N。假设充电负荷均分于整个地区,用户在需要充电的时间只会从N家充电站中选择一家进行充电。
基于服务范围的实时定价优化的详细过程如下:
1)读取某地区N个充电站基础数据与日前风光数据,根据熵值法得到各指标的权重大小,进一步根据式(2)计算得到在不加入电价影响下的各充电站的初始综合实力,同时在日前风光数据的基础上加上功率偏差得到实时风光预测数据。
2)根据充电站各项指标数据计算得到式(4)中各项参数,再根据式(3)计算得到各充电站服务范围的初始场强En.k。
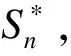
4)根据初始充电需求占比建立充电价格与充电需求之间的关系式以及充电站收入模型,如式(8)与式(10)所示。每个充电站的需求与收入都会受各个充电站电价变化的影响。
5)建立考虑利润率与功率偏差率两方面的多目标实时定价模型。实时优化目标如式(12)所示,包括两部分,第一部分以所有充电站总利润率最大为目标,第二部分以功率偏差率最小为目标,以减少的功率偏差率表示目标函数:
maxE=max(ωnEp_lr+ωbcEp_pc)
(12)
(13)
(14)
式中:Ep_lr表示充电站的利润率;Ep_pc表示减少的功率偏差率;ωn表示各个充电站利润率的权值;ωbc表示功率偏差率的权值;Pe为充电站购电成本;Pn.w为充电站运营维护成本;ΔPt为风光实时与日前的功率偏差量。优化决策量为Pn.t,表示t时刻各充电站的电价。
优化模型约束条件如下:
功率偏差率需满足界限约束,如式(15)所示:
(15)
式中:Pev.t为日前充电负荷预测值。
各充电站的市场需求不超过日前充电负荷预测值,满足市场需求约束,如式(16)所示:
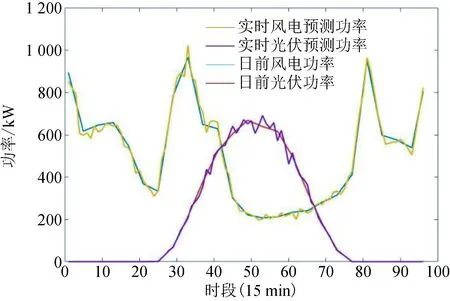
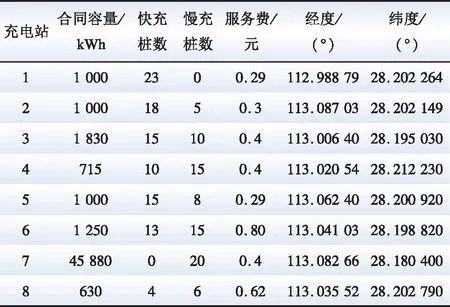
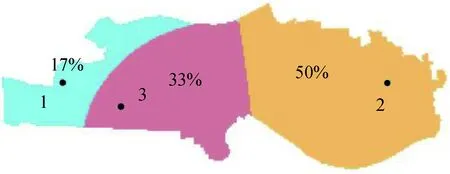
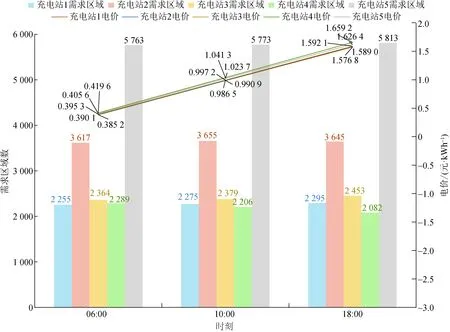
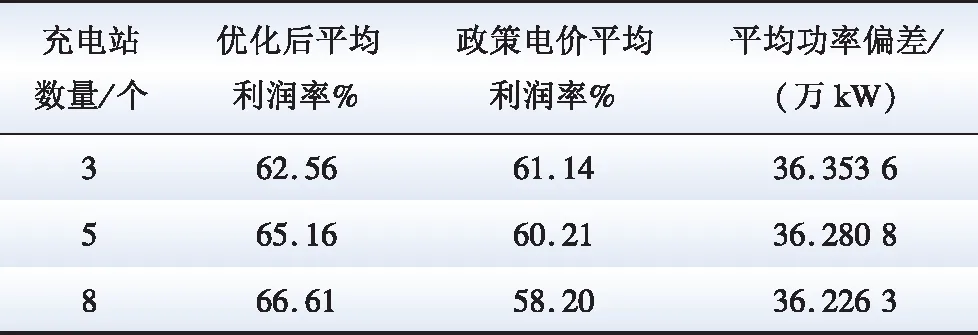
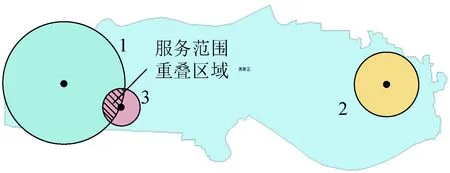
0 (16) 风光实时与日前的功率偏差量满足功率偏差约束,如式(17)所示: ΔPt=PW.t+PL.t-Pw.t-Pl.t (17) 式中:PW.t和Pw.t分别表示t时刻的实时和日前风电出力大小;PL.t和Pl.t分别表示t时刻光伏实时和日前出力。ΔPt>0表示t时刻风光实时出力大于日前预测出力,需要引导用户充电增大充电负荷以消纳多出的风光出力;ΔPt<0表示t时刻风光实时出力小于日前预测出力,需要鼓励用户减少充电负荷。 所有充电站的充电负荷满足充电负荷约束,如式(18)所示: (18) 式中:ξ为充电负荷约束参数,表示各充电站的负荷之和不应该超过以ξ为参数的日前充电负荷的区间;ξl为充电负荷约束下限系数;ξh为充电负荷约束上限系数。 充电价格满足电价约束,如式(19)所示: Pr.n(1-φl)≤Pn.t≤Pr.n(1+φh) (19) 式中:φl为电价下限界限系数;φh为电价上限界限系数。 6)参考国家能源局综合司发布的《电力现货市场基本规则(征求意见稿)》中的相关内容[32],以15 min为分辨率将一天分为96个时间点。并以1 h为运行周期,基于MATLAB调用CPLEX与YALMIP对以利润率与功率偏差率为对象的多目标优化模型进行优化求解,得到96个时间点N个充电站的动态电价Pn.t,以及各充电站优化后的利润率与功率偏差率。 7)由于优化计算得到了各时刻的实时电价Pn.t,此时电价具有了时间属性,因此再将实时电价加入到充电站的综合实力评价模型式(2)中,随着动态电价的实时变化波动,充电站的综合实力Cn与服务范围场强也同样被赋予了时间属性,会随之发生变化,因此再根据式(1)与(3)仿真可以得到96个时间点N个充电站的实时动态服务范围Sn.t=(S1.t,S2.t,…,SN.t)。基于此分别选取处于峰谷平电价时段来分析充电站服务范围的动态变化规律。 具体的求解流程如图3所示。 图3 实时定价优化及求解流程图Fig.3 Real-time optimization flow chart 以长沙市芙蓉区充电站数据为例进行仿真验证,本文充电站数据均来自于国网湖南省经济技术研究院科研项目“电动汽车充电设施网络与配电网协同有序建设的研究与实践”,风光出力为全湖南省的数据。采用ArcGIS软件进行绘图操作,对长沙市芙蓉区地图进行经纬度精度为0.000 5°的栅格划分,得到芙蓉区16 288个市场区域。从芙蓉区选取三个代表性的充电站进行算例计算,三个充电站的基础数据如附录表A1所示。基于图2指标体系,利用熵值法得到充电站各项指标权重如附录表A2所示。SPSS因子分析后综合得分大于0的充电站个数tmax=143,根据式(2)得到各充电站的综合实力如附录表A3所示。基于Isard公式(1),计算当不考虑充电价格交互影响时,各充电站初始服务范围与初始占比,如图4所示。 图4 各充电站初始占比与服务范围Fig.4 Initial radiation range of charging station 由图4可以看出,在不考虑充电价格的影响时,充电站2的服务范围最大。由于充电站2的快充桩数量较多,且周围较近的区域没有其他充电站与其竞争,因此其服务范围占据了芙蓉区一半的区域。 由附录表A3可知充电站1的综合实力最大,所以它与充电站3服务范围之间的界限呈现一个向内弯曲的弧度,距两个充电站越远的区域更多的属于充电站1。但由于自身位置偏僻,而且周围有充电站3的竞争挤压,导致其服务范围在三个充电站中最小。 设定三个充电站的需求函数q1.t、q2.t、q3.t,选取式(18)充电负荷约束中ξl=0.8、ξh=1.2,式(19)电价界限约束中φl=φh=0.1。根据国家能源局综合司发布的《关于进一步推动新型储能参与电力市场和调度运用的通知》政策,湖南省代理购电价格Pe为0.462 44元/kWh。选取各充电站一天的维护成本P1.w=600元、P2.w=550元、P3.w=500元。根据项目数据,某典型日的日前风光出力数据如附录图A1所示,设定风光预测误差为5%,实时出力满足正态分布。根据第3节的流程计算充电站在峰谷平时段的平均电价,如表1所示。 表1 充电站各时段平均电价Table1 Average electricity price of charging station in each period 由表1可知,充电站1与充电站2的电价均比政策电价低,而充电站3的电价比政策电价高。这主要是由于充电站1与2的综合实力更高,意味着电动汽车用户会更多的关注充电站1与2,对于价格变化更敏感,则式(8)中政策电价价差影响系数kp.n更大,低于政策电价能够带来更多的充电需求与利润。而由于充电站3的综合实力最小,用户对其价格变化的关注度最低,故充电站3会通过设定比政策电价更高的价格(在峰时段上涨了0.013 7元/kWh,平时段上涨0.023 5元/kWh)来维持收益。 分析峰谷平时段充电站市场区域变化。选取06:00、10:00、18:00三个时间点,得到三个时间点各充电站所占市场区域数如附录图A2所示。由图中可以看出充电站2由于竞争压力小导致服务范围变化不明显,随价格变化的服务范围主要体现在充电站1与3之间,因此,本文主要分析充电站1与3服务范围的变化,其所占市场区域数与价格变化如图5所示。 图5 充电站1与3所占区域数与电价变化Fig.5 The number of areas occupied by charging stations 1 and 3 and the change of tariff 加入了实时电价的影响后,充电站1由于综合实力更高,同时两者电价相差仅为0.020 0元/kWh,因此所占市场比例从图4的17%上升到20%(06:00市场区域数为3 212),相应的离充电站1较近的充电站3由于实力更小,其部分服务范围被夺走,从33%下降到29%。 随着峰谷平电价的变化,充电站1由于电价的上升,所占市场区域数从谷时段到峰时段减少了245个,相对地,充电站3则增加了253个所占市场区域数。前面已经说明了用户对于综合实力更高的充电站价格敏感度更高,因此,当综合实力更高的充电站1电价升高后,充电站1的用户下降的数量相比于充电站3更快,导致服务范围的变化更大。 由此可见,充电价格与服务范围受多方面因素影响:综合实力、地理位置、周围竞争对手数量等都会产生相应的影响。 增加充电站数量以分析不同充电站数量对于服务范围、功率偏差率与利润率的影响并验证4.1节的相关结论。以5个充电站与8个充电站为例,充电站的数据如附录表A4所示,初始服务范围如附录图A3所示。 计算5个充电站的充电电价与综合实力,如表2所示。8个充电站的充电电价与综合实力如附录表A5所示。 由表2可知,综合实力较小的充电站4在各个时段相较于其他充电站电价更高,设定比政策电价更高的价格能够获得更多的利润。而充电站1与2由于自身综合实力最大,用户对其关注度更高,适当地降低充电电价能够获得更多的充电需求与利润,符合4.1节的结论。 同样选取06:00、10:00、18:00三个时间点,得到三个时间点各充电站所占市场区域数,如图6所示。 图6 5个充电站所占区域数与电价变化Fig.6 The number of areas occupied by 5 charging stations and the change of tariff 通过图6与附录图A3可以看出,随着峰谷平电价的上升,充电站3、4由于位置居中且周围有较多充电站的存在,同时自身综合实力较小,导致服务范围变化较大,分别增减了89、207个市场区域数,同样根据附录图A4中8个充电站的案例也可以验证以上结论。 按照6 h一间隔选取4个时间点,各时间点的充电站利润率与功率偏差率如表3所示。 表3 不同充电站数量下平均利润率与功率偏差Table 3 Average profitability and power deviation of charging stations at different volumes 从表3中可以看出,随着参与竞争的充电站数量增加,采用政策电价获得的利润会逐步减小,凸显了引入考虑服务范围的定价策略的重要性。参与实时优化的充电站数量从3个增加到5个和8个后,利润率分别增加了2.60%、4.05%,功率偏差分别减少了764、1 309 kW。这主要是由于充电站数量的增多带来了更多的优化调节空间,参与到优化的充电需求总量变高,充电站之间利润分配更加合理,因此提升了充电站的利润率,也更好地弥补了风光功率偏差。但因为充电站总体数量较少的缘故,对于整个湖南省的功率偏差调整效果不明显。 为保证本文所提方法的优越性,对其他服务范围划分方法与本文所提划分方法的结果进行对比。本文选取基于改进Wilson模型的服务半径计算方法与断裂点模型的服务范围划分方法进行对比分析。 4.3.1 基于改进Wilson模型的服务范围划分 基于改进Wilson模型对各充电站服务范围进行划分,可以得到充电站服务范围,如下式所示: (20) (21) 图7 基于Wilson模型的服务范围划分Fig.7 Wilson model-based service range division 由图7可以看出,采用改进Wilson模型得到的各充电站服务范围呈现规则圆形,不符合现实中的复杂情况。并且充电站1与3之间服务范围重叠的区域无法判断属于哪个充电站,此外整片区域还存在大量没有被覆盖的区域,市场划分判断不准确,对用户起不了指导作用,因此本文所提服务范围划分方法更具有优越性。 4.3.2 基于断裂点模型的服务范围划分 基于断裂点模型对各充电站进行服务范围划分,断裂点为两个充电站连线之间服务范围的边界点,基于此可以得到基于断裂点模型的服务范围划分模型如下: (22) 式中:Dn表示断裂点到充电站n的距离;Dnm表示充电站n与m之间的距离。 基于式(22)可以计算得到各充电站距离断裂点的距离:充电站1相对于充电站2的断裂点距离D1=1.044 2 km,充电站2相对于充电站3断裂点距离D2=4.126 7 km,充电站3相对于充电站2的断裂点距离D3=3.814 4 km。基于此得到基于断裂点模型的服务范围如图8所示。 图8 基于断裂点模型的服务范围划分Fig.8 Service range division based on breakpoint model 由图8可以看出,基于断裂点模型得到的服务范围划分虽然能将整个区域覆盖,但站与站之间通过直线划分无法直接判断充电站的实力大小,且缺乏考虑电价变化带来的影响,因此本文所提方法更具有优越性。 本文提出了一种基于Isard法的充电站服务范围动态划分方法与定价策略。通过加入动态优化电价来模拟服务范围的变化,能够更好地体现综合实力、充电电价与需求之间的关系。以长沙市芙蓉区为实例仿真得到了如下结论: 1)综合实力更大的充电站能够得到更多电动汽车用户的关注,用户对于充电站价格的波动变化更敏感,通过设定比政策电价更低的充电价格,往往能够带来更多的利润。 2)充电站密集的区域竞争更加激烈,价格的波动引起的服务范围变化更加明显。相反,充电站稀疏的区域服务范围更加稳定,充电价格的波动对于服务范围的影响更小,为运营商未来充电设施的修建规划提供了参考意见。 3)随着参与市场竞争的充电站数量增加,政策电价的利润空间会逐步减小,可以通过基于服务范围制定实时电价,提高各充电站的利润。 附录A 图A3 各充电站初始占比与服务范围Fig.A3 Initial radiation range of charging station 图A4 8个充电站所占区域数与电价变化Fig.A4 The number of areas occupied by 8 charging stations and the change of tariff 图A1 风光日前实时出力预测Fig.A1 Scenery predicts the output in real time 图A2 各充电站所占区域数Fig.A2 Number of areas occupied by each charging station 表A1 充电站相关参数Table A1 Charging station related parameters 表A3 充电站初始综合实力Table A3 Comprehensive strength of charging station 表A4 8个充电站相关参数Table A4 The 8 charging stations related parameters 表A5 8个充电站各时间段充电价格与综合实力Table A5 The number of demand areas occupied by 8 charging stations for each time period 表A6 Wilson模型服务范围划分法的参数Table A6 Parameters for the Wilson model service range method 
4 算例仿真
4.1 充电站初始服务范围划分与定价策略


4.2 充电站数量对服务范围影响
4.3 与其他服务范围划分方法对比分析

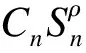
5 结 论