双馈变速抽水蓄能全工况转换过程建模与仿真
2023-09-27井浩然李佳赵红生徐秋实姚伟王博
井浩然,李佳,赵红生,徐秋实,姚伟,王博
(1. 强电磁工程与新技术国家重点实验室(华中科技大学电气与电子工程学院),武汉市 430074;2. 国网湖北省电力有限公司经济技术研究院,武汉市 430077)
0 引 言
随着我国能源战略转型的持续推进,新能源装机占比持续增加,但其波动性和间歇性特点给电网带来如调峰和消纳等诸多问题[1-9]。抽水蓄能是缓解这些问题的重要手段,尤其是双馈变速抽水蓄能技术,其更宽功率调节范围和更快功率响应速度能够更好地发挥抽水蓄能的调峰、调频和调相作用[10-12]。因此,利用双馈变速抽水蓄能技术促进新能源消纳已成为国内外学者及工程界关注的热点[13-16]。而建立双馈变速抽水蓄能系统的动态模型是研究其动态响应特性的重要基础。
当前,国内外双馈变速抽水蓄能建模相关的研究主要集中在发电工况和抽水工况稳态运行的建模上。文献[17]建立了抽水工况双馈变速抽水蓄能的简化机电暂态模型,研究了机组的动态响应特性;文献[18]研究了发电工况和抽水工况双馈变速抽水蓄能的机电暂态模型在刚性与弹性水动态模型下的动态响应;文献[19]分别建立了双馈变速抽水蓄能机组的数学模型和控制模型;文献[20]详述了抽水蓄能系统各部分的动态建模;文献[21]推导了双馈变速抽水蓄能机组的数学动态模型;文献[22]建立了双馈变速抽水蓄能机组的详细模型,基于模型研究发电工况和抽水工况下控制策略的动态性能。现有文献只对双馈变速抽蓄的某种工况进行了建模,但针对双馈变速抽水蓄能工况转换繁多、启停频繁的特点,罕有文献对其工况转换过程进行建模研究。
在电网日常调度中,常常需要抽水蓄能机组从发电工况过渡到抽水工况或从抽水工况过渡到发电工况,所以有必要针对双馈变速抽水蓄能整个工况转换过渡过程进行建模研究。因此,本文开展双馈变速抽水蓄能全工况转换过渡过程建模相关研究工作。首先建立双馈变速抽水蓄能系统的机电暂态模型,包括交流励磁电机模型、换流器模型、水泵水轮机和控制系统模型;然后,针对发电工况和抽水工况下的启动-稳态运行-停机完整的工况转换过渡过程进行建模;最后,通过Matlab/Simulink仿真验证所建双馈变速抽水蓄能全工况模型的运行特性。
1 双馈变速抽水蓄能系统建模
双馈变速抽水蓄能系统由三部分组成,其一是电气部分,包括交流励磁电机、网侧换流器和转子换流器;其二是水力、机械部分,包括可逆水泵水轮机、压力管道水动态、调速器与导叶伺服机构;其三是控制部分,包括工况选择器、转速与导叶开度优化器、转子侧换流器控制与网侧换流器控制。双馈变速抽水蓄能系统的结构如图1所示。
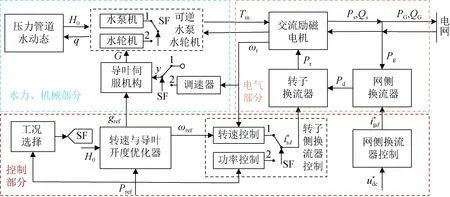
图1 双馈变速抽水蓄能系统结构Fig.1 Structure of doubly-fed induction machine based variable-speed pumped storage
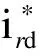
1.1 交流励磁电机建模
文献[23]在dq坐标系下建立交流励磁电机模型,不考虑磁链饱和、磁滞和涡流等现象,将转子参数折算至定子侧,定、转子电压方程为(定、转子绕组均采用电动机惯例):
(1)
式中:usd、usq和urd、urq分别为定子和转子电压的d轴、q轴分量;isd、isq和ird、irq分别为定子和转子电流的d轴、q轴分量;Rs、Rr分别为定子和转子电阻;p、ω分别为微分算子和系统同步转转速;ψsd、ψsq和ψrd、ψrq分别为定、转子磁链d轴、q轴分量。
(2)
式中:Ls、Lr、Lm分别为定子等效自感、转子等效自感和定转子等效互感。
运动方程和电磁转矩方程简化式为:
(3)
式中:Te为电磁转矩;J为转动惯量;np为电机极对数;D为阻尼系数。
1.2 换流器建模
换流器的主要功能是驱动交流励磁电机。网侧换流器的主要功能是保持直流母线电压稳定、保证输入电流正弦和控制输入功率因数,采用电网电压定向矢量控制可以有效实现网侧换流器dq轴电流的解耦控制,其控制框图如图2所示[24]。
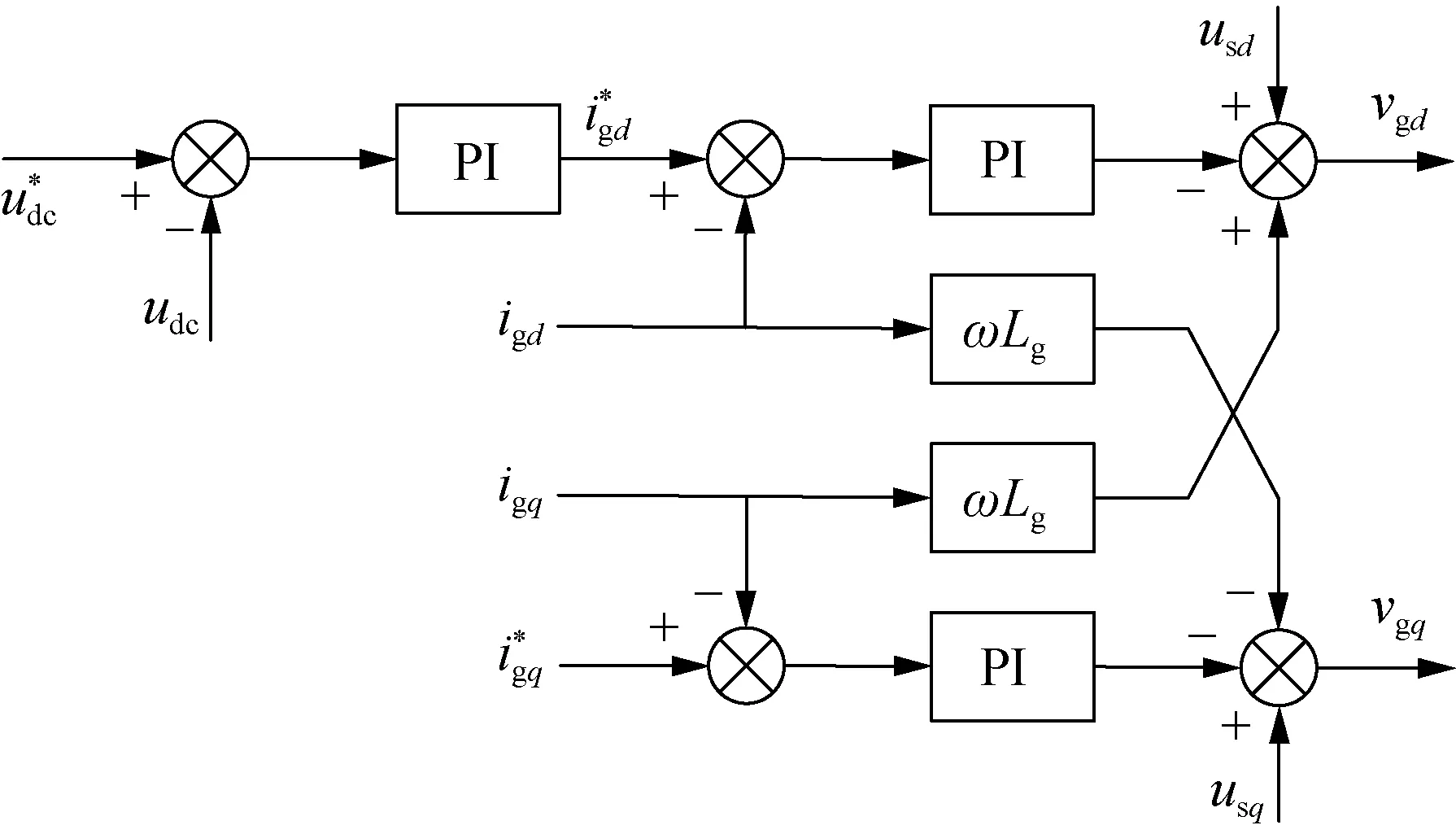
图2 网侧换流器控制框图Fig.2 Control block diagram of grid-side converter
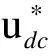
转子换流器的主要功能是控制交流励磁电机定子输出的有功、无功功率,而定子输出的有功、无功功率和转子电流的dq轴分量密切相关,所以同样需要有效控制转子电流的dq轴分量。考虑到转子电压幅值会动态变化,而定子电压幅值基本恒定,采用定子磁链定向矢量控制可以实现转子dq轴电流的解耦控制,其控制框图如图3所示。在发电工况下,转子换流器优先控制有功功率,当机组的有功功率参考值发生变化时,换流器迅速响应,控制机组的有功功率快速跟踪参考值;在抽水工况下,机组吸收的有功功率由转速决定,转子换流器优先控制转速,当机组有功功率参考值发生变化,首先根据水泵水轮机综合特性曲线得到最优转速,换流器迅速响应,控制机组转速达到最优转速,从而调节机组有功功率。
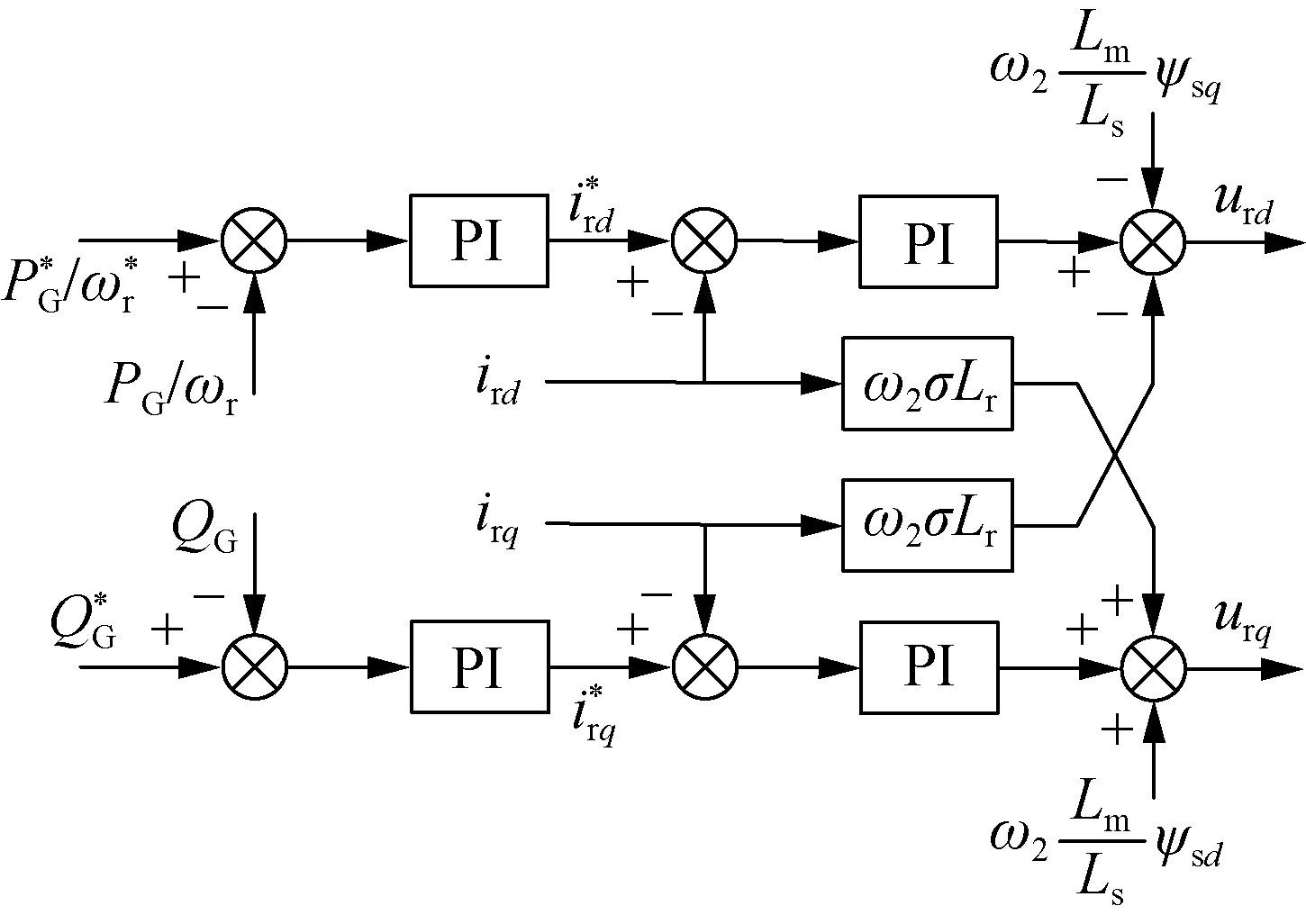
图3 转子换流器的控制框图Fig.3 Control block diagram of rotor-side converter
1.3 水泵水轮机与水动态建模
在发电和抽水工况下,水泵水轮机分别作为水轮机和水泵,通过对水在上下水库之间进行转移实现水动能和机械能的转换。在发电模式和抽水模式下,水泵水轮机与水的互动方式不同,导致动态特性不同,因此需要建立不同的动态模型。采用刚性水击模型描述输水管道动态特性。
1.3.1 发电模式下动态模型
在发电模式下,水泵水轮机的动态模型可以表示为[20]:
(4)
式中:Hdg为动态水头;Qd为动态流量;Tw为水流惯性时间常数;Hsg为静态水头;Hlg为水头损失;ηg为发电模式下的效率;Qnl为空载流量;Pmg为发电模式下的机械功率;Tmg为发电模式下的机械转矩。
水流通过输水管道由于摩擦效应产生的水头损失与动态流量的平方成正比,有:
(5)
式中:fp为压力管道摩擦系数;ft为水洞摩擦系数。
发电工况下的效率ηg与水头、流量和转速有关,可以用以下多项式表示[25-26]:
(6)
1.3.2 抽水模式下动态模型
在抽水模式下,水泵水轮机的动态模型可以表示为:
(7)
式中:Hsp为静态扬程;Hlp为扬程损失;Pmp为抽水模式下的机械功率;ηp为抽水模式下的效率;Tmp为抽水模式下的机械转矩。
动态扬程由动态流量和转速决定,可近似为以下二次多项式[27]:
(8)
式中:bi(i∈{0, 1, 2})为二次多项式系数,根据抽水模式下特性曲线拟合得到。
由于导叶摩擦效应和管道阻力所造成的扬程损失可以表示为:
(9)
式中:fg为导叶摩擦系数;Gmax为最大导叶开度。
抽水工况下的效率ηp取决于动态流量和转速,可以用以下多项式表示[17]:
(10)
式中:ci(i∈{0, 1, 2, 3})为多项式系数,根据抽水模式下特性曲线拟合得到。
1.4 调速器与导叶伺服系统
通过控制导叶开度可以控制机组机械功率。导叶开度控制环节包括导叶开度调节器和导叶开度伺服,其控制框图如图4所示。
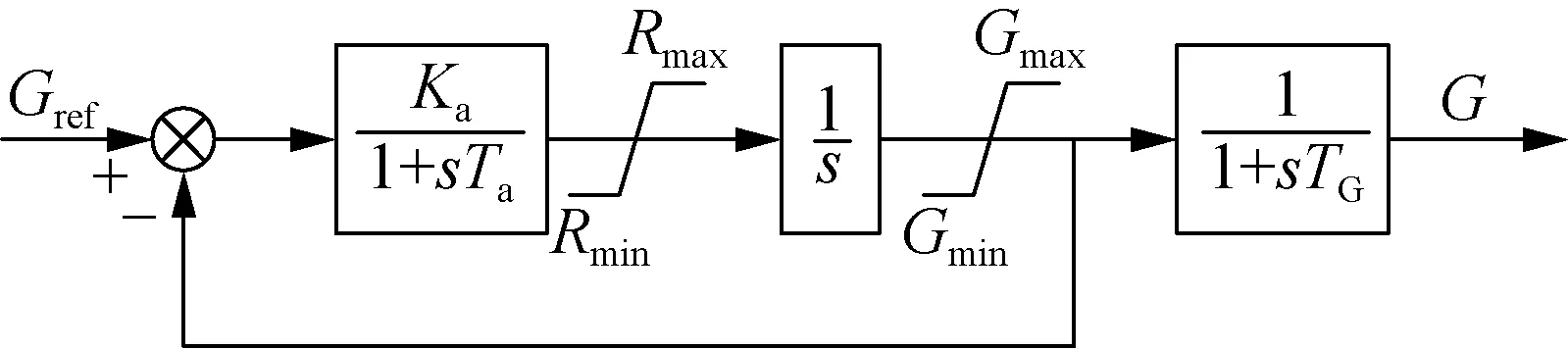
图4 导叶开度控制框图Fig.4 Control block diagram of gate opening
图4中:Gref为导叶开度参考值;Ka为导叶开度调节器的比例系数;Ta为导叶开度调节器的时间常数;Rmax为导叶开度变化速率最大限值;Rmin为导叶开度变化速率最小限值;Gmax、Gmin分别为导叶开度最大和最小限值;TG为导叶开度伺服的时间常数。
在发电模式下,机组功率由转子换流器控制,转速由调速器通过调节导叶开度来控制。调速器通常采用并联式PID控制器,其动态模型如图5所示。
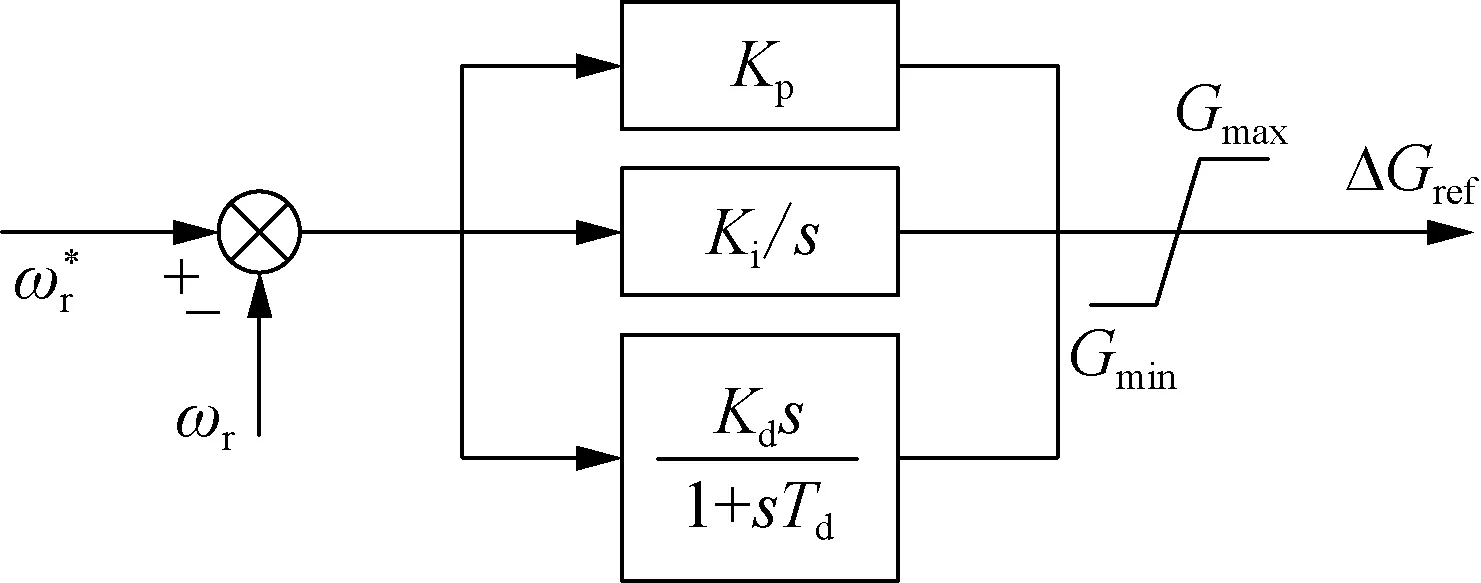
图5 调速器控制框图Fig.5 Control block diagram of speed governor
图5中:Kp、Ki、Kd分别为调速器的比例、积分和微分系数;Td为微分环节的时间常数;ΔGref为导叶开度参考值变化量。
1.5 转速与导叶开度优化器
通常变速抽蓄在处于正常运行状态时,功率和水头变化范围较大。当偏离额定水头或功率时,机组运行效率下降。变速抽蓄在不同的水头和功率调度值下,根据水泵水轮机的综合特性曲线,通过优化转速和导叶开度来追踪最大效率。文献[18]对转速与导叶优化器采用线性方程进行近似,其表达式为:
(11)
式中:Hsg(p)为静态水头;系数di、ei(i∈{0, 1, …, 4})基于机组最优运行曲线拟合得到,在部分运行范围与实际运行特性差异较大。本文对水泵水轮机模型进行300余次实验,确定其实际运行特性,据此采用三次方程进行近似,其近似式为:
(12)
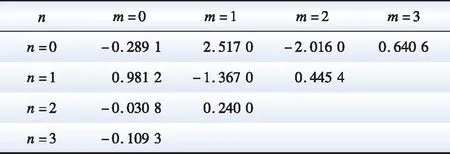
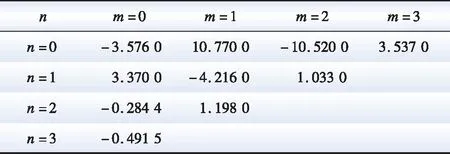
式中:ωref、gref分别为转速和导叶开度参考值;ai、bj(i,j∈{0, 1,…,10})为多项式系数;m,n∈{0,1,2,3}为H0和Pref阶数。
2 机组工况转换控制
双馈变速抽水蓄能机组通常有5种稳定运行工况,分别是停机、发电、抽水、发电调相和抽水调相,具有工况转换繁多、启停频繁的特点。抽水蓄能机组极少情况处于长时间调相运行工况,所以本文仅针对停机、发电和抽水3种典型运行工况转换过程进行研究。机组工况转换过程可分为以下阶段:发电/抽水工况启动、发电/抽水工况增减负荷、发电/抽水工况稳态运行、发电/抽水工况停机、发电/抽水工况切换。
2.1 工况选择
变速抽蓄正常运行范围一般为0.6~1.0 pu,当需要机组发出或吸收的功率小于正常运行范围的最小值时,机组一般会根据经济性选择不启动或与其他抽蓄协调运行,本文只考虑不启动情况。
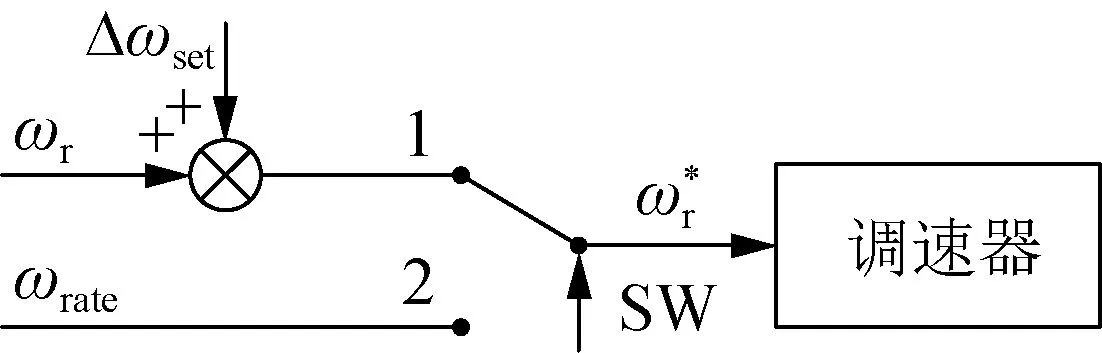
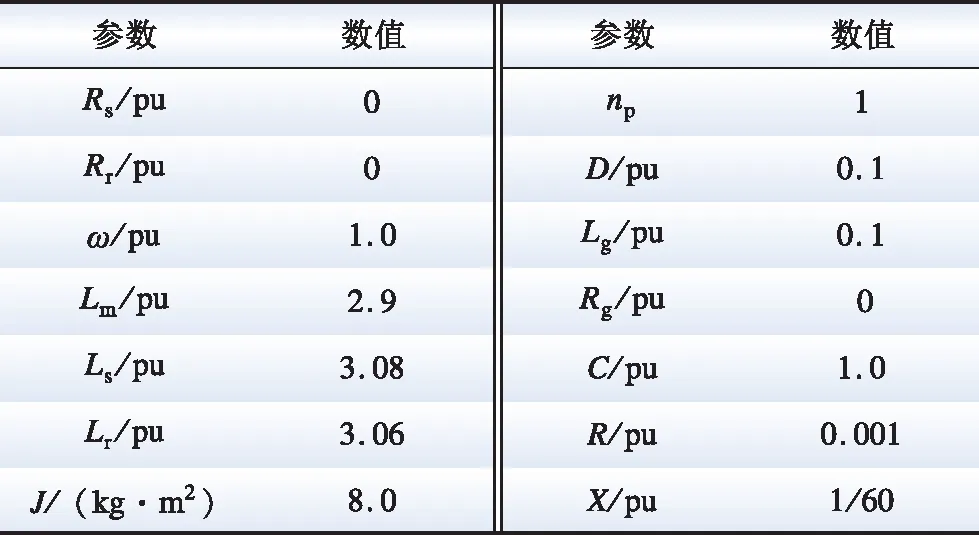
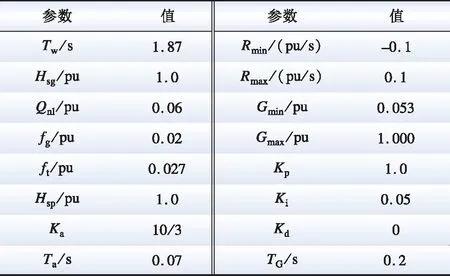
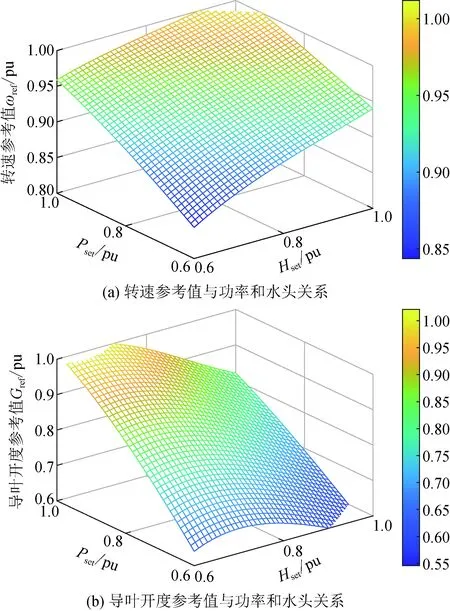
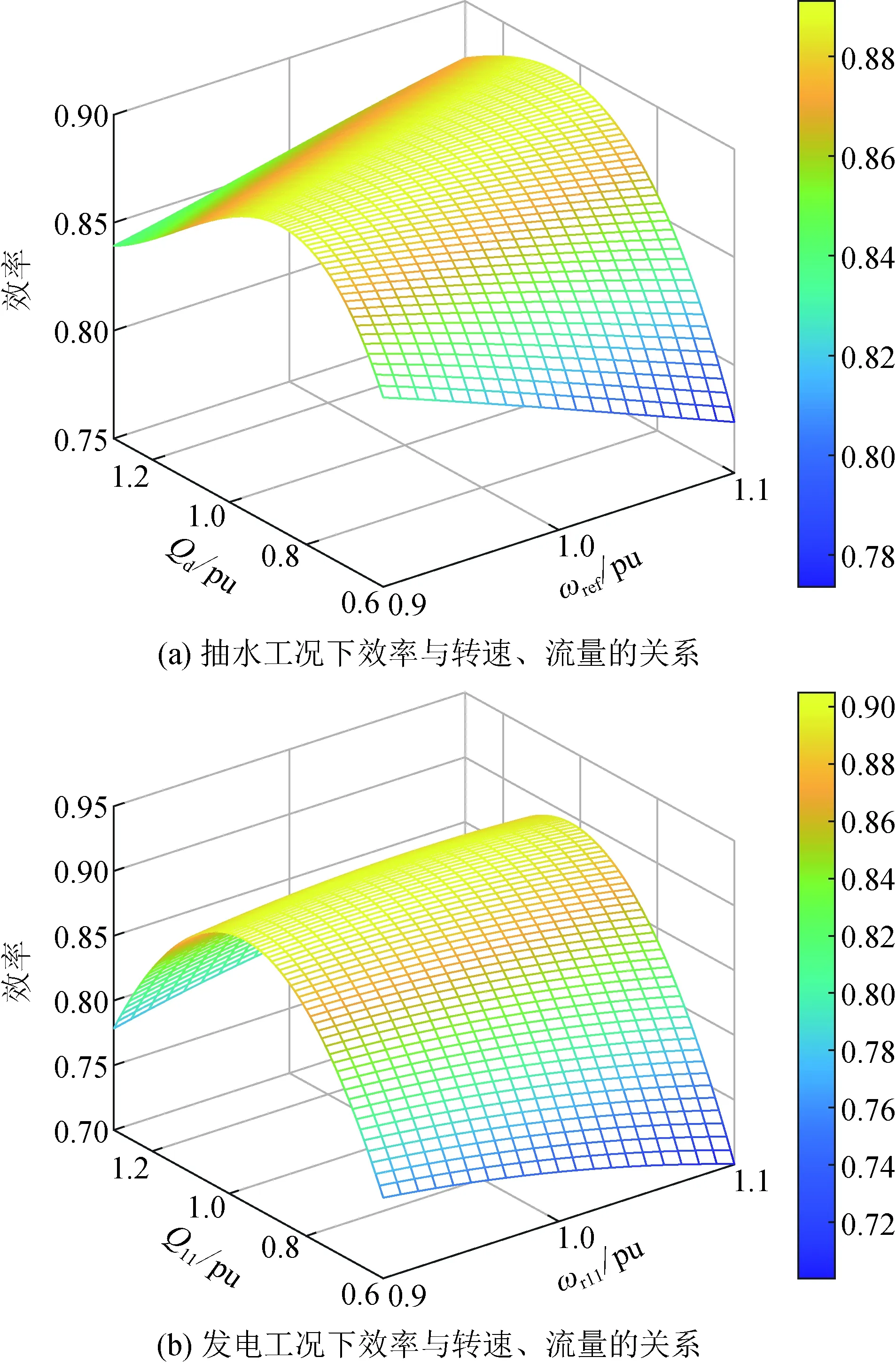
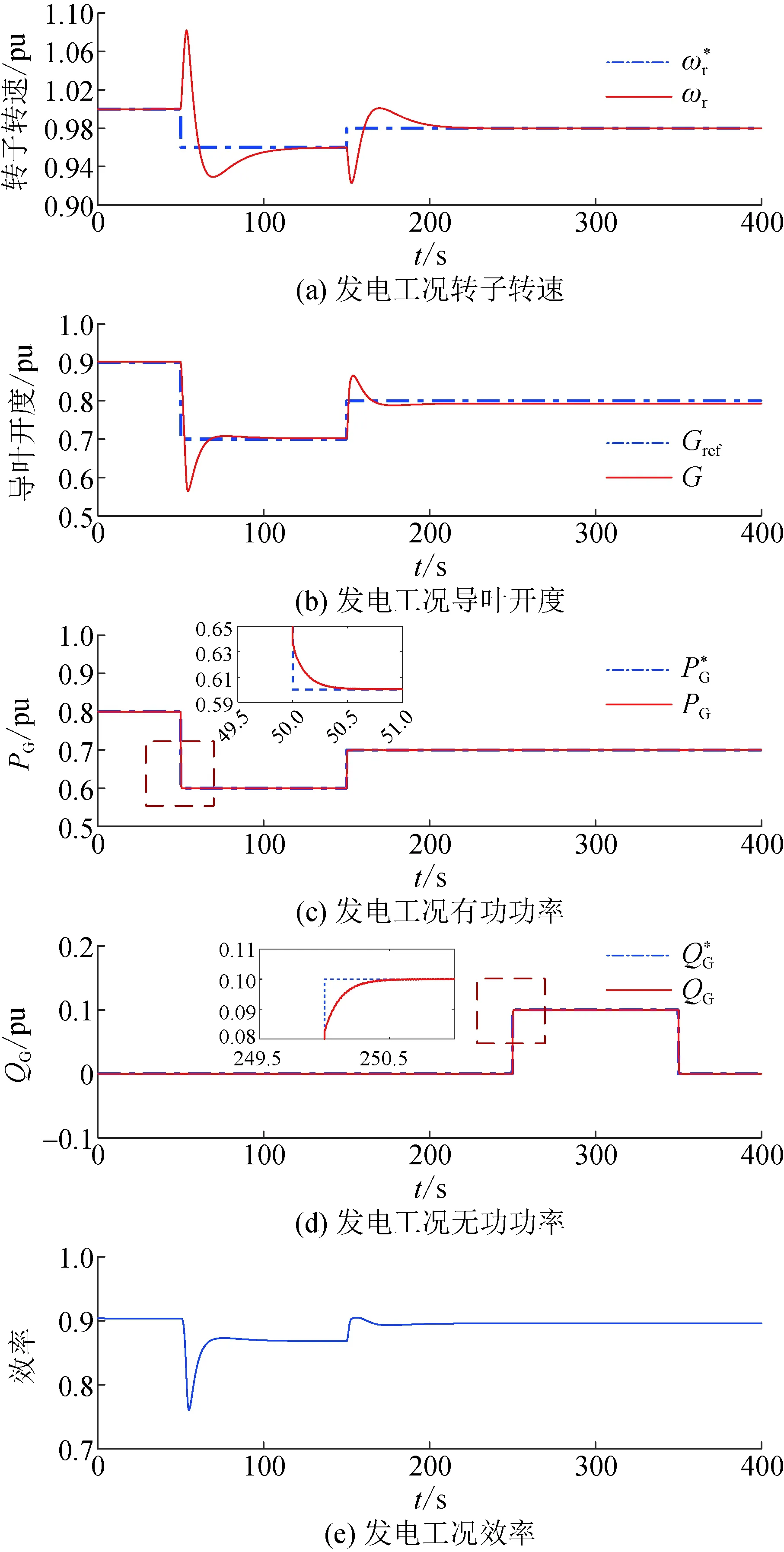
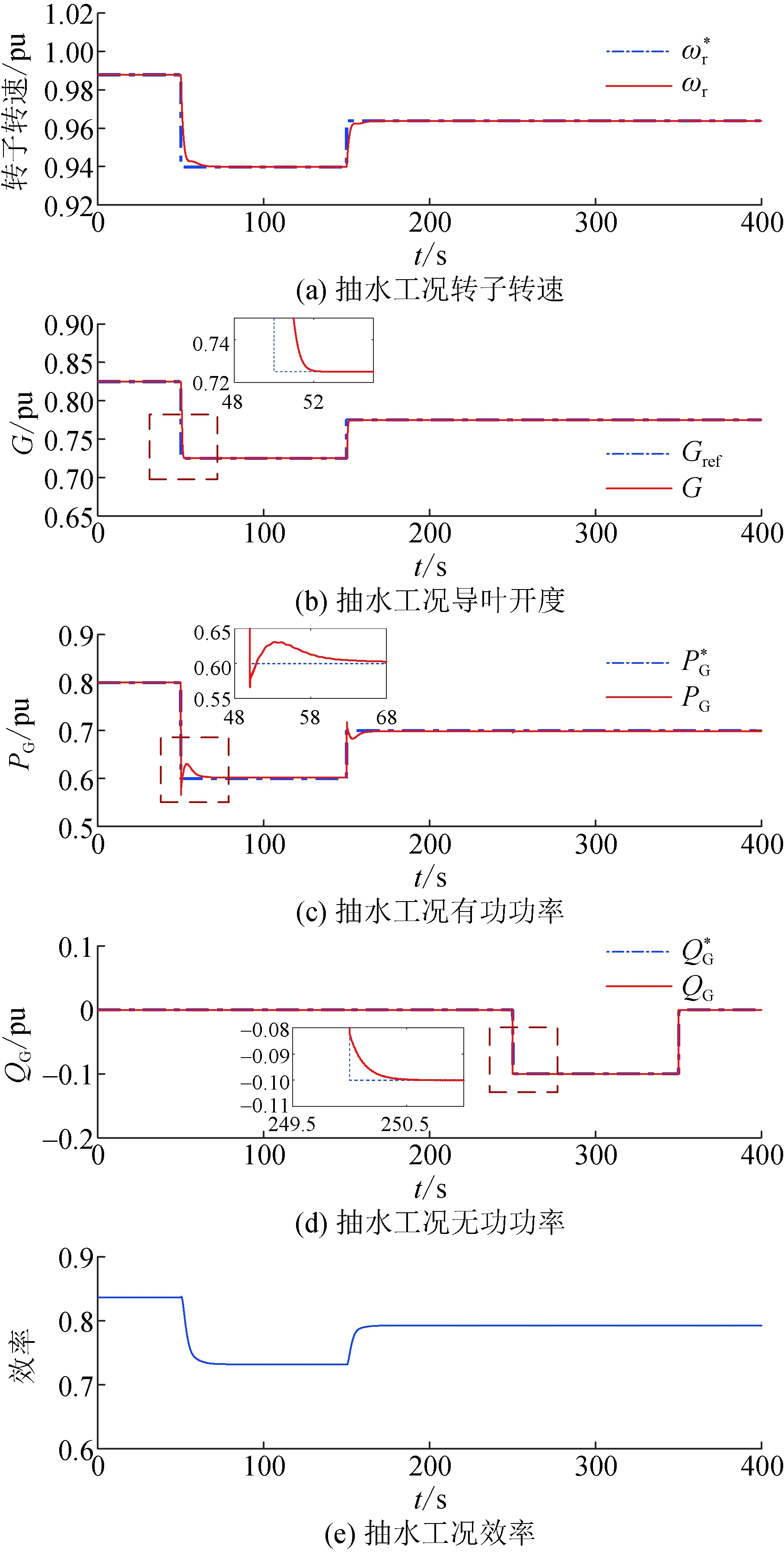
在电网日常调度中,若有功功率参考值Pref=0,不需要变速抽蓄出力,或有功参考值处于Pmin- 图6 工况选择示意图Fig.6 Diagram of working condition selection 实际工程中,抽水蓄能机组发电工况启动时,首先短接定、转子三相绕组,然后通过调速器将导叶开度增大,利用水泵水轮机拖动机组转子正向加速,当转速到达额定转速附近加速过程完成,接着打开定、转子三相短接开关,通过转子换流器调节定子电压完成并网操作。 图7 发电工况启动控制框图Fig.7 Starting control block diagram of generation mode 抽水蓄能机组抽水工况的启动方式有2种:一种方式是直接并网启动,通过转子换流器控制电机进行启动,此方式需要从电网吸收功率;另一种方式是脱网启动,首先短接定子三相绕组,转子换流器加三相对称反相序电流,电机反向旋转,当反向转速到达额定转速附近加速过程完成,接着打开定子三相短接开关,通过转子换流器调节定子电压完成并网操作,此方式功率波动较小。 在发电工况下,机组功率由转子换流器控制,转速由调速器通过调节导叶开度来控制,而导叶开度的响应速度较慢,所以功率的变化会导致转速的波动,而且功率变化量和变化速率越大,转速波动越剧烈。为了避免转速波动过大,在发电工况增减负荷阶段,转子换流器的功率参考值以斜坡形式增大或减小。 在抽水工况下,机组启动后转速由转子换流器控制保持稳定,需要调节导叶开度增大机组输入功率。在抽水工况增减负荷阶段,导叶开度参考值同样以斜坡形式增大或减小。 在发电/抽水稳态运行阶段,机组能够直接、解耦地控制有功功率和无功功率,在此阶段需要考虑机组稳定运行条件限制和有功无功调节能力。 当机组调速范围过大时,机组效率会降低,为保证机组安全稳定运行,避免水头/扬程过高或过低导致机械应力过大损害转动部件,需要考虑调速和水头/扬程的限制。同时也要考虑到水泵水轮机与交流励磁电机的容量限制而产生的有功无功限制。 在发电/抽水工况减负荷后,待定子电流为0,并网断路器断开,机组脱网,然后短接定子绕组,在转子换流器励磁电压作用下电机产生制动转矩,机组转速降至0。在发电/抽水工况停机阶段,机组与电网交换的功率为0。 在仿真分析中,机组减负荷后功率为0,机组进入空载阶段,忽略空载摩擦,因此认为电磁转矩Te=0,同时机械转矩Tm=0,但此时转速不为0。在停机过程开始电机转子运动模型添加制动转矩Db,根据转子运动方程,有(J/np)dωr/dt=-(D/np+Db)ωr,通过制动转矩实现转速速降,待转速为0后切除制动转矩从而完成停机过程。 当电网有功调度发生工况转换时,需要抽水蓄能机组从发电工况过渡到抽水工况或从抽水工况过渡到发电工况。在仿真分析中,为实现发电/抽水工况切换控制,通过工况选择模块,通过有功调度值的大小选择不同水泵水轮机动态模型和控制方式,如图1所示。 SF=1时,机组处于抽水工况,当需要过渡到发电工况时,首先在抽水工况减负荷、停机,然后SF=2,接着在发电工况启动、增负荷,最后处于稳态运行,实现从抽水工况过渡到发电工况;同理,SF=2时,机组处于发电工况,当需要过渡到抽水工况时,首先在发电工况减负荷、停机,然后SF=1,接着在抽水工况启动、增负荷,最后处于稳态运行,实现从发电工况过渡到抽水工况。 本文的研究重点在于单台双馈变速抽水蓄能机组工况切换控制,因此,仿真算例设置为单台100 MW变速抽蓄机组连接无穷大系统。根据第1节和第2节的分析,在Matlab/Simulink上搭建如图1所示的单机双馈变速抽水蓄能系统模型,电气系统和水力系统参数如表1和表2所示[28]。其中,无穷大系统电压d轴分量Usd为1 pu,电压q轴分量Usq为0,R、X分别为无穷大系统等效电阻和等效电感。 表1 双馈变速抽水蓄能机组电气系统参数Table 1 Parameters for electrical system of DFIM-VSPS 表2 双馈变速抽水蓄能机组水力系统参数Table 2 Parameters for hydraulic system of DFIM-VSPS 将表1和表2的参数赋予双馈变速抽蓄机组并进行实验,可得其部分运行特性。 基于本模型获得的实验数据对转速与导叶开度优化式进行三次拟合得到式(12),转速与导叶开度多项式系数矩阵如表3、表4所示,m为H0阶数,n为Pref阶数,m+n≤3,拟合曲面如图8所示。低扬程时采用较低转速及较大的导叶开度,高扬程时采用较高转速及较小的导叶开度运行,机组可获得较高效率。水轮机与水泵工况下效率曲面如图9所示。 表3 转速优化式系数Table 3 Coefficient of roter speed optimization 表4 导叶开度优化式系数Table 4 Coefficient of guide vane opening optimization formula 图8 转速与导叶开度优化拟合曲面Fig.8 Speed and vane opening optimization fitting surface 图9 效率与转速和流量的关系Fig.9 Dependence of efficiency on speed and flow rate 图10展示了机组“停机—发电—停机—抽水—停机”的完整工况转换过程。机组需经过发电启动阶段、发电增负荷阶段、发电减负荷阶段、发电停机阶段、抽水启动阶段、抽水增负荷阶段、抽水减负荷阶段、抽水停机阶段。仿真中,取发电工况的转速和功率为正,则抽水工况的转速和功率为负。 设置50 s时机组启动进入发电工况,100 s时开始增负荷至0.8 pu,400 s时开始减负荷,550 s时停机。750 s时机组启动进入抽水工况,800 s时开始增负荷至0.8 pu,1 100 s时开始减负荷,1 250 s时停机。 在发电工况启动阶段,导叶开度G>0,此时电机的机械转矩Tmg>0,电磁转矩Te=0,转速迅速增大至1.0 pu附近,不考虑并网有功功率波动,在此阶段机组输入到电网的有功功率为0;在增负荷阶段,导叶开度逐渐增大,在转子换流器的控制下,机组的有功功率能平滑地达到设置值,在此阶段由于电磁转矩和机械转矩响应速率不一致,转速有一个下降过程;在减负荷阶段,导叶开度逐渐减小至空载开度,机组的有功功率能平滑地减小为0,在此阶段转速有一个上升过程;在停机阶段,在制动转矩的作用下,转速迅速减小至0,在此阶段机组输入到电网的有功功率为0。 在抽水工况启动阶段,在转子换流器的控制下,机组从电网吸收有功功率,此时电机的电磁转矩Te<0,机械转矩Tmp=0,转速迅速增大至1.0 pu附近;在增负荷和减负荷阶段,机组的有功功率能平滑地增大和减小;在停机阶段,在制动转矩的作用下,转速迅速减小至0,在此阶段机组吸收的有功功率为0。 初始阶段水头为1 pu,当管道中有水流过时,水头开始变化。当机组处于发电工况,水从上水库流至下水库,水头减小;当机组处于抽水工况,水从下水库抽至上水库,扬程增大。水流量的大小会影响水头变化的快慢。 从仿真结果可以看出,双馈变速抽水蓄能系统模型能平滑地实现从停机至发电或抽水再到静止的完整工况转换过程。 图11为发电模式下有功功率和无功功率参考值变化时机组的动态响应特性。仿真中,机组初始有功输出为0.8 pu,无功输出为0 pu,设置50 s时有功输出减小0.2 pu,150 s时有功输出增加0.1 pu,250 s时无功输出增加0.1 pu,350 s时无功输出减小0.1 pu。 图11 发电模式下动态响应Fig.11 Dynamic responses of generation mode 如图11所示,当有功参考值阶跃减小时,在转子换流器的控制下,机组发出的有功功率迅速减小至给定值,由于导叶开度响应较慢,机组电磁功率转化为转子动能,转子加速;当有功参考值阶跃增大时,在转子换流器的控制下,机组发出的有功功率迅速增大至给定值,由于导叶开度响应较慢,机组转子动能转化为电磁功率,转子减速;在有功参考值变化阶段,在导叶开度和转速优化控制下,导叶开度和转速参考值也相应改变,通过调速器和导叶伺服的控制,机组转速和导叶开度能准确地跟踪参考值;当给定的无功参考值改变时,机组发出的无功功率能快速响应,迅速到达给定值;当机组有功功率改变时,无功功率没有变化,同样在机组无功功率改变时,有功功率没有变化,说明机组实现了有功无功的解耦控制。 图12为抽水模式下有功功率和无功功率参考值变化时机组的动态响应特性。从仿真结果可以看出,在抽水工况,当有功无功参考值改变时,机组吸收有功无功能快速响应,迅速到达给定值,实现了有功无功解耦控制;同时在导叶开度和转速优化控制下,当有功参考值改变时,机组能跟踪最佳导叶开度和最优转速,机组效率能维持在较高水平,当有功功率偏离额定工况越远,效率越低。 图12 抽水模式下动态响应Fig.12 Dynamic responses of pumping mode 本文针对双馈变速抽水蓄能机组工况转换繁多、启停频繁的特点,在Matlab/Simulink仿真软件上搭建了可进行工况转换的双馈变速抽水蓄能机组暂态模型。仿真结果表明所建变速抽蓄机组模型具有以下特点: 1)双馈变速抽水蓄能系统模型在发电工况和抽水工况能平滑地实现从静止至稳态运行至静止完整的工况转换过程。 2)双馈变速抽水蓄能系统模型在发电工况和抽水工况稳态运行时,能快速响应有功无功参考值改变,实现有功无功解耦控制,同时能追踪最佳导叶开度和最优转速。 3)双馈变速抽水蓄能系统模型能平滑从发电工况过渡到抽水工况和从抽水工况过渡到发电工况,实现不同运行工况切换过程。 后续研究将基于所搭建的模型致力于研究双馈变速抽水蓄能源网协调策略。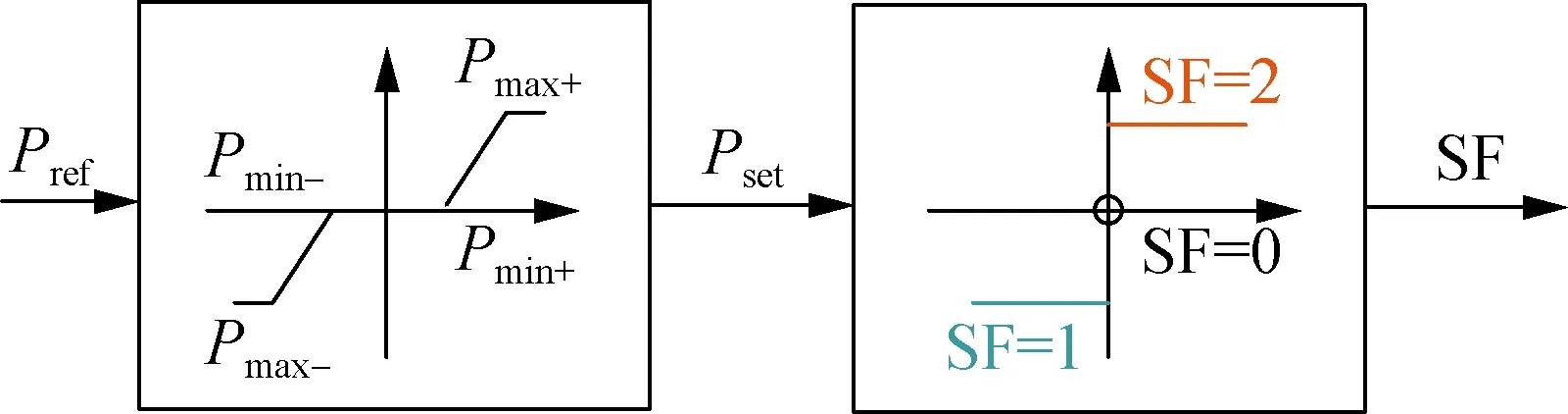
2.2 发电/抽水工况启动
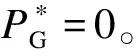
2.3 发电/抽水工况增减负荷
2.4 发电/抽水工况稳态运行
2.5 发电/抽水工况停机
2.6 发电/抽水工况切换
3 仿真分析
3.1 双馈变速抽蓄运行特性
3.2 发电/抽水工况切换
3.3 发电/抽水模式下稳态运行
4 结 论
