计及DSSC的含新能源电网静态电压稳定性分析

仇晨光, 张振华, 李蓝青 , 李彦柳, 周霞, 马道广

(1. 国网江苏省电力有限公司,南京市 210008;2.南京邮电大学碳中和先进技术研究院,南京市 210023)

0 引 言

以新能源为主体的新型电力系统得到广泛发展,大规模新能源呈现高比例并网的发展趋势。但高渗透率新能源并入电网场景下发生的电压崩溃事故将造成巨大的经济损失[1],大规模新能源接入会对电网静态电压产生影响,因此解决大规模新能源发电时的电压稳定问题是当前研究人员重点关注的问题,其中静态电压稳定问题尤为显著[2-3]。

针对解决大规模新能源并入电网后的静态电压稳定问题,目前已有较多的文献利用分析静态电压稳定特征的方式量化系统电压稳定性,同时提出提升静态电压稳定性的策略。传统静态电压稳定特征分析是以潮流计算为基础,通过寻找静态电压稳定临界点,计算当前系统节点的电压稳定裕度,常用的有连续潮流法[4-7]、崩溃节点法[8-9]和非线性规划法[10-11]。文献[12-13]基于节点电压曲线、无功功率变化曲线,将系统临界稳定运行的节点电压变化值和无功功率变化值加权和作为综合电压稳定指标,评估内部负荷变化时电力系统的电压稳定性。文献[14-15]根据输电线路上功率与线路首尾节点电压之间的关系,利用潮流计算方程根的判别式提出静态电压稳定指标。文献[16-17]按照简化系统思路和分析配电网的单条线路模型,在潮流计算的基础上,针对配电网安全稳定问题提出静态电压稳定指标。现有的静态电压稳定指标大多是基于单一固定的模型进行设计,忽略了负荷波动、新能源发电不确定性等因素,难以充分反映当电力系统受到扰动后整体的运行状态,限制了静态电压稳定指标的通用性。

伴随着电力电子技术的发展,柔性交流输电技术(flexible AC transmission system, FACTS)在调节线路潮流、改善静态电压稳定性方面的研究更加深入[18-19],文献[20]分析了高比例光伏并入电网对系统安全稳定运行的影响,并提出通过对新能源电网配置FACTS装置的策略改善薄弱线路的静态电压稳定性。文献[21-23]通过安装可控串联补偿装置(thyristor controlled series compensation ,TCSC)和静止同步补偿器(static synchronous compensator,STATCOM)装置在电压薄弱节点处,调节线路潮流从而提升系统整体静态电压稳定性[24-25]。上述文献鲜有将FACTS装置与电力系统潮流计算方程结合提出新的电压稳定指标,并且未考虑新能源电网配置FACTS装置后对电力系统安全稳定运行性能的提升。分布式静态串联补偿器(distributed static series compensator, DSSC)作为目前先进的柔性交流输电装置之一[26-28],为电网的安全运行提供了一种电压支撑和功率调节的方法,DSSC可通过调节线路潮流的方式有效缓解高比例新能源并网后对系统安全所带来的危害[29-30]。

针对上述问题,本文探讨了DSSC对高渗透率新能源电网静态电压稳定特征的影响,从系统静态电压稳定性方面评估DSSC发挥的控制潮流效能。为分析配置DSSC的潮流控制对系统静态电压稳定性的提升效果,本文首先通过等值功率注入法建立含DSSC装置的等效模型,得到考虑DSSC的潮流计算方程;其次,针对新能源并入电网后所带来的安全稳定性问题,基于潮流计算方程提出系统静态电压稳定性指标,分析不同容量新能源并入电网后配置DSSC对当前电力系统薄弱节点静态电压稳定性的影响;最后通过IEEE 30节点验证分析DSSC的潮流控制对系统静态电压稳定性的影响。

1 DSSC结构及模型

1.1 DSSC原理及结构

DSSC是一种用于潮流控制的分布式柔性交流输电技术(distributed flexible AC transmission system, D-FACTS)单相设备,省去设备间的绝缘设计直接耦合于输电线路上,容量一般为0～10 kVA。DSSC是包含单匝变压器、复合开关(指反并联晶闸管或双向晶闸管和常闭机械开关的组合)、滤波器、单相电压源逆变器、直流电容、控制保护模块,通信模块的新型电力电子装置,DSSC结构示意图如图 1 所示。通过将多个小容量、单相逆变器直接与输电导线相连,主动调节传输线路阻抗值,从而实现对电网有功潮流的控制。

DSSC的基本原理为当传输线路无电流通过或者电流相对较小时,复合开关处于闭合状态。在传输线路电流较大时, DSSC可通过控制电路保持设备较低的工作电流,以此确保单相电压源逆变器的安全。当传输线电流达到相应值后,DSSC通过单相电压源逆变器向电网注入一个连续且可控的电压,从而改变阻抗动态调节线路潮流。此电压包含两个分量,一个分量用于正交线路电流,形成注入电压线路所需的阻抗值,使等效阻抗呈现电感、电容等特性,从而调节线路输送的有功和无功功率潮流,实现阻尼功率振荡、提高暂态稳定性等控制目标;另一分量与线路电流同相,用于实现补偿逆变器的功率损耗和维持逆变器直流电压稳定。同时逆变器对于系统暂态电压稳定性进行无功补偿,减少系统内潮流阻塞的线路潮流,降低一些发电机出力或进行切机处理,减少系统故障率,以此来提高系统暂态电压稳定性。DSSC的等效电路图如图2所示,其中US为系统等效电源;XDSSC为单匝变压器等效漏抗;UDSSC为逆变器输出电压;ILine为系统电流;UL为负载侧电压。SL=PL+jQL为负载功率;PL、QL为负荷的有功功率及无功功率。

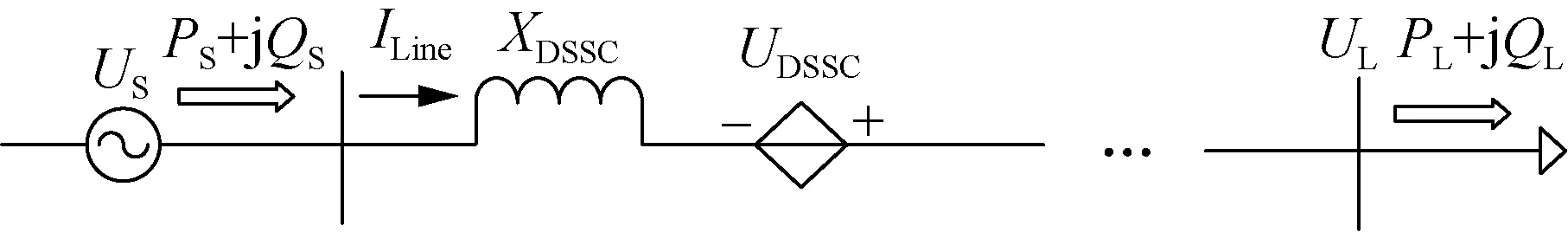
图2 DSSC等效电路图Fig.2 DSSC equivalent circuit diagram

1.2 DSSC等效电路

DSSC耦合于输电线路上,线路中流过的有功功率P可以表示为:

(1)

式中:V1和V2分别为线路首末端的电压幅值;X为输电线路的电抗;δ为线路首末端之间的相角差。

DSSC配置到系统相应线路后,相当于注入一个与线路电流垂直的电压。因此,线路中流过的有功功率P′可以表示为:

(2)

式中:VDSSC为 DSSC 注入线路的电压。

考虑到线路两端电压接近1.0 pu,并且线路两端的相角差较小,有sinδ≈δ,cos(δ/2)≈1,DSSC的直流有功潮流P″可以表示为:

(3)

可以看出:DSSC 注入电压的相位影响线路潮流的变化,通过增减注入电压的大小来调整各个输电线路潮流分布差异。

2 考虑新能源接入的静态电压稳定分析

2.1 新能源发电机组等效模型

本文以风电机组为例,并入电网的数学模型如图3所示。图3中X′SG为传统同步机组等值阻抗;X′W为风电机组等值阻抗;XS为输电线路阻抗;U为并网后电网母线电压。

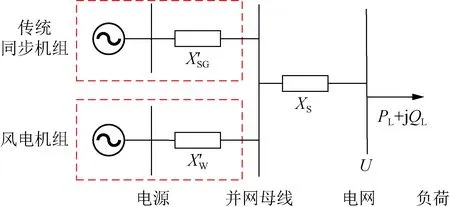
图3 风电并网数学模型Fig.3 Mathematical model of wind power grid connection

(4)

式中:XSG为系统中仅有传统机组并网时的等值阻抗;η为当前系统风电机组渗透率,定义为风电出力/总出力;λ为当前风电发电机组与传统机组的阻抗比值。

2.2 新能源接入系统的静态电压稳定机理

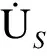
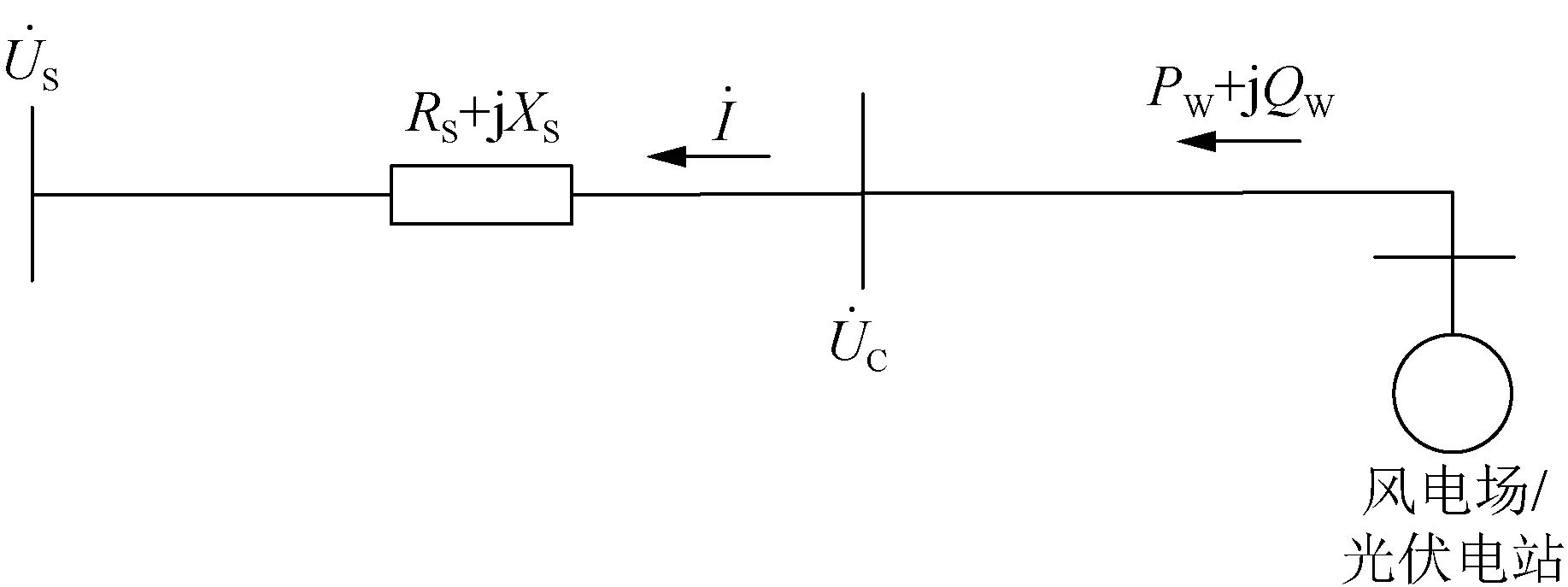
图4 新能源接入电网的简化图Fig.4 Simplified diagram of new energy access to power grid

(5)

新能源并网点向电网发出功率后可得:

(6)

(7)

式中:θ为相位角;结合式 (6)与式 (7)化简后可得:

(8)

(9)

(10)

忽略传输电阻RS,可得:

(11)

由式(11)可知:新能源并入电网功率与接入电网的电压之间为负相关,随着新能源功率的增加,电网有功功率与节点电压相关联的灵敏度逐渐增大,系统电网的电压稳定性明显降低。

3 含DSSC的系统静态电压稳定评估

3.1 计及DSSC的潮流计算方法

对于任何复杂的电力系统,其系统都可以简化为共包含n个节点,(m-1)个PQ节点,(n-m)个PV节点,以及一个平衡节点,则潮流平衡方程可以表示为:

(12)

式中:ΔPi是系统第i个节点有功注入功率量;ΔQi是系统第i个节点无功注入功率量;Ui是系统第i个PV节点电压值;Gij、Bij是i-j支路导纳的实部和虚部;Pi为系统第i个节点初始有功功率;Qi为系统第i个节点初始无功功率;Uj为系统第j个PV节点电压值;θij为i-j支路的相位角差值。

简化后的潮流平衡方程为:

(13)

式中:ΔP为系统有功注入功率量;ΔQ为系统无功注入功率量;H、N、J、L为雅可比矩阵的转置向量;Δθ为节点电压的相角差;ΔU为节点电压差。

将DSSC配置在线路i-j的节点i侧,并且对配置DSSC所在线路两端的潮流方程进行修改,其他节点潮流方程保持不变。修改后的潮流方程为:

(14)

式中:Pi(ini)、Qi(ini)、Pj(ini)、Qj(ini)分别是DSSC注入系统节点i、j的有功和无功功率。

装有DSSC的线路传输功率为:

(15)

式中:UD为配置DSSC线路的节点电压;δD为配置DSSC线路的相角;g、b为支路导纳的实部和虚部;bc为配置DSSC线路导纳的实部。

本文侧重于评估DSSC接入后对新能源并网安全稳定运行的影响,因此采用DSSC恒定容量控制模式:

HD-Href=0

(16)

式中:HD为当前线路所配置DSSC的容量实际值;Href为当前线路所配置DSSC的容量给定值。DSSC的逆变电压可由容量参考值Href与串联线路电流额定值Imax表示:

(17)

式中:Umax为DSSC接入线路的最大逆变电压。电网中各线路电流额定值Imax均已知,因此本文可将控制目标修改为:

UD-Umax=0

(18)

因此,系统每接入一套 DSSC都将增加两个控制变量UD和δD,同时增加内部运行约束式 (15)和控制目标式 (18)。

3.2 系统静态电压稳定指标

新能源并入电网后改变系统潮流,从而会影响系统静态电压稳定。新能源潮流分布会影响到静态电压稳定性,从而影响系统安全稳定运行。

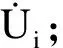
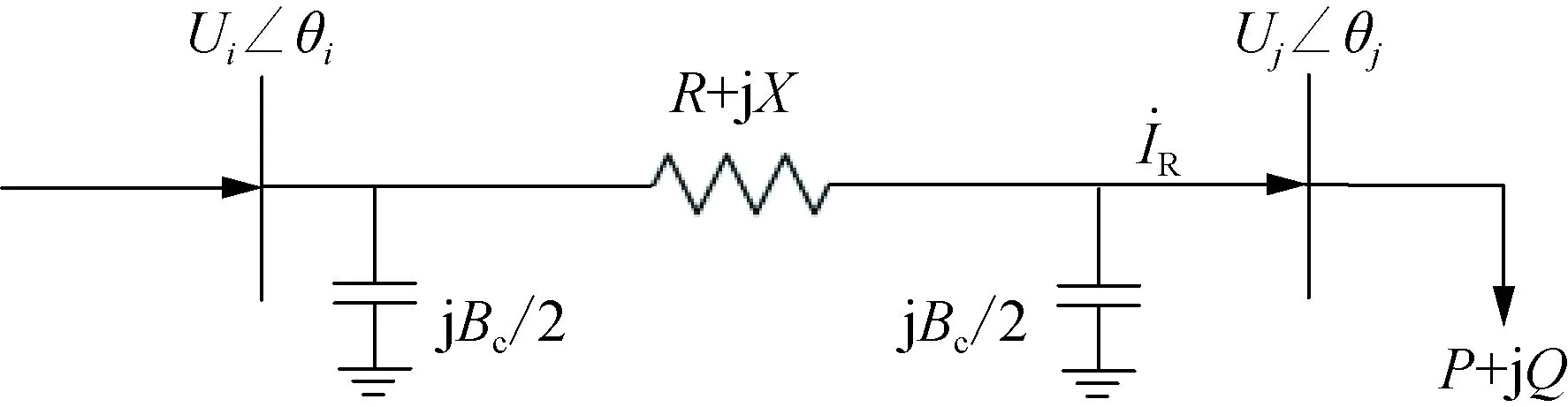
图5 输电网简化模型图Fig.5 A simplified model diagram of the transmission network

从而可得相应电压方程:

(19)

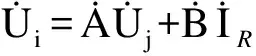
(20)

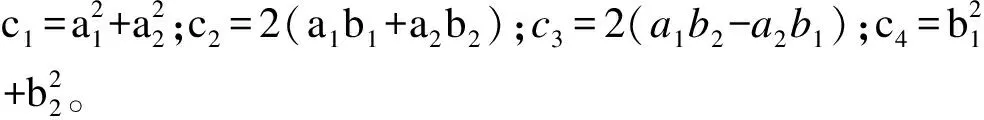
进一步计算可得:

(21)

DSSC装置通过调节线路潮流的方式改善系统静态电压稳定性。线路末端负荷节点j电压稳定值可表示为:

LVSI=min(dvc1,dvc2,…,dvcN)

(22)

式中:LVSI为线路末端负荷节点电压稳定值;dvcj为节点j电压稳定裕度;N是系统中以j为节点末端的支路总数。电网整体电压稳定性的强弱与节点电压稳定裕度成正比,以节点为末端的支路稳定裕度为0,即支路电压稳定性处于临界状态,越过临界运行状态将会在此节点出现电压崩溃的现象,同时丢失输电线路原本的平衡节点。系统在不同运行状态下的最小节点电压稳定裕度被定义为系统最薄弱节点,此节点安全裕度能够反映系统整体的静态电压稳定性,即:

μVSI=min(LVS1,LVS2,…,LVSk)

(23)

式中:μVSI为系统整体的静态电压稳定性;k是系统中负荷节点的个数。本文采用的薄弱节点是在负荷的增长过程中系统节点电压崩溃概率最大的节点。

4 算例分析

4.1 新能源渗透率对静态电压稳定值的影响

本文在IEEE 30 节点系统接入风电、光伏新能源,采用MATLAB仿真验证本文所提指标的正确性和合理性,如图6所示。

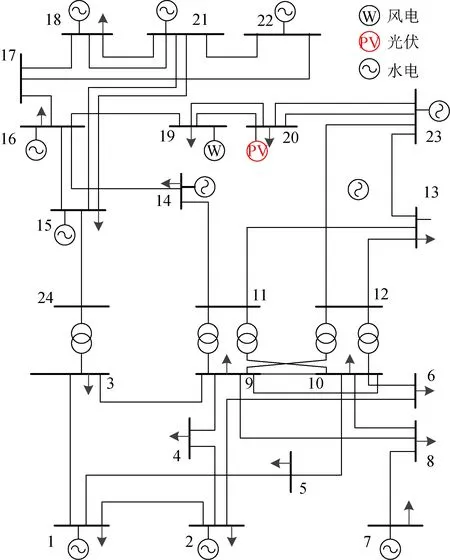
图6 新能源接入的IEEE 30节点系统Fig.6 IEEE 30-node system for new energy access

此外,本文使用的IEEE 30节点系统假设如下:关键节点的有功和无功负荷以恒定功率因数的模式增长,发电机和新能源以初始基准值等比例承担负荷增长;新能源发电机组逐渐替代发电机电源,研究新能源不同接入点对系统静态电压稳定性的影响以及接入DSSC对静态电压稳定性的影响。

图7为本文所使用的IEEE 30节点系统在初始状态下各节点的值。由图可知,节点19在初始运行状态下的值为0.331 5 pu,可认为此系统该节点电压安全稳定裕度最小,在整个系统中处于最薄弱位置。伴随着新能源并入电网的负荷逐步增加,该节点发生电压崩溃的概率最大,危及整体电网的安全稳定运行。

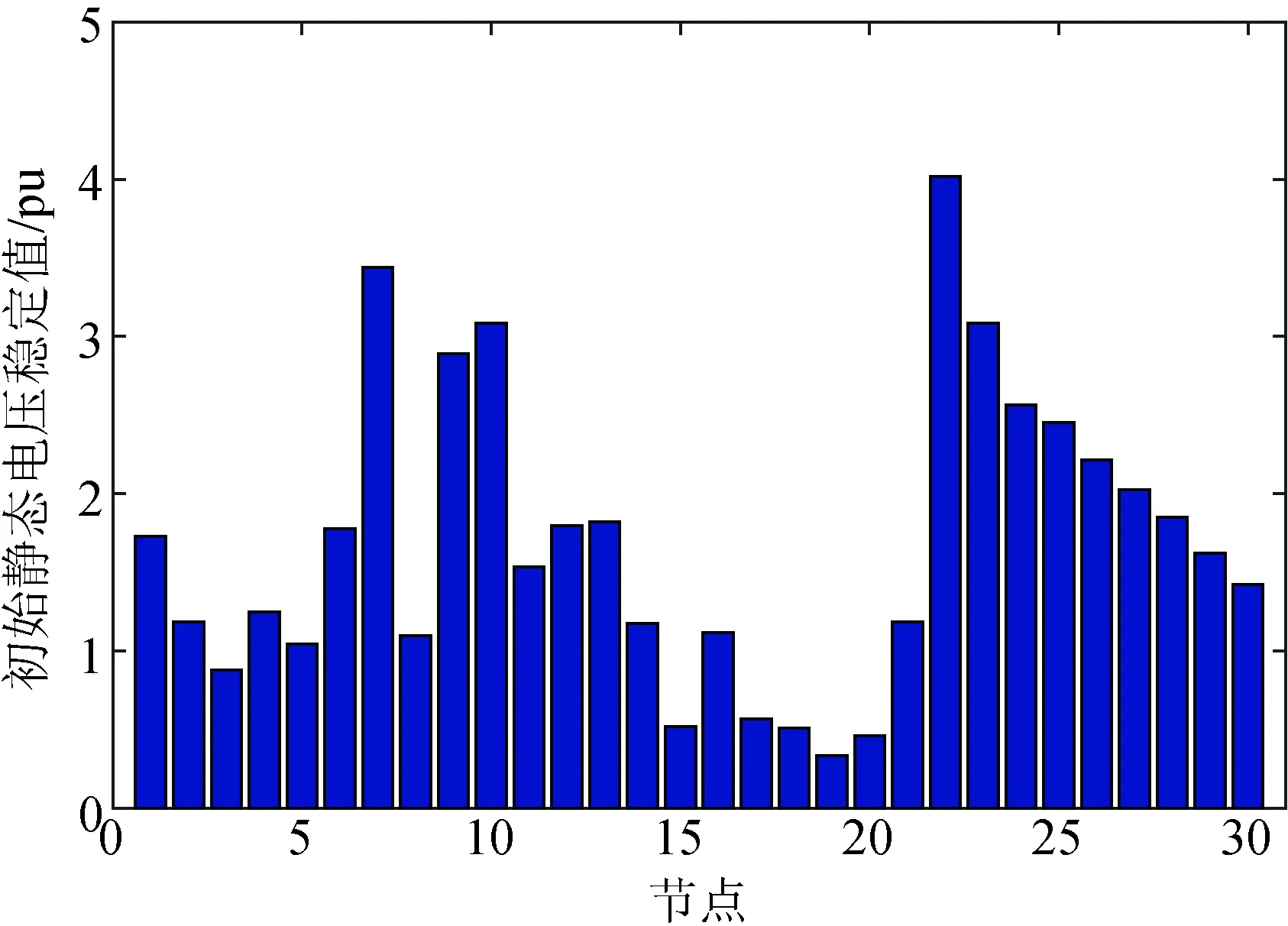
图7 初始状态下各节点的静态电压稳定值Fig.7 Static voltage stability value of each node in initial state

图8是新能源渗透率增长过程中不同节点的静态电压稳定值,系统接入新能源后影响整个系统的安全稳定性,其中新能源节点19处的μVSI值下降了0.075,节点15处的μVSI值下降了0.058 8,这表明距离新能源负荷节点越近电压下降速率越快。

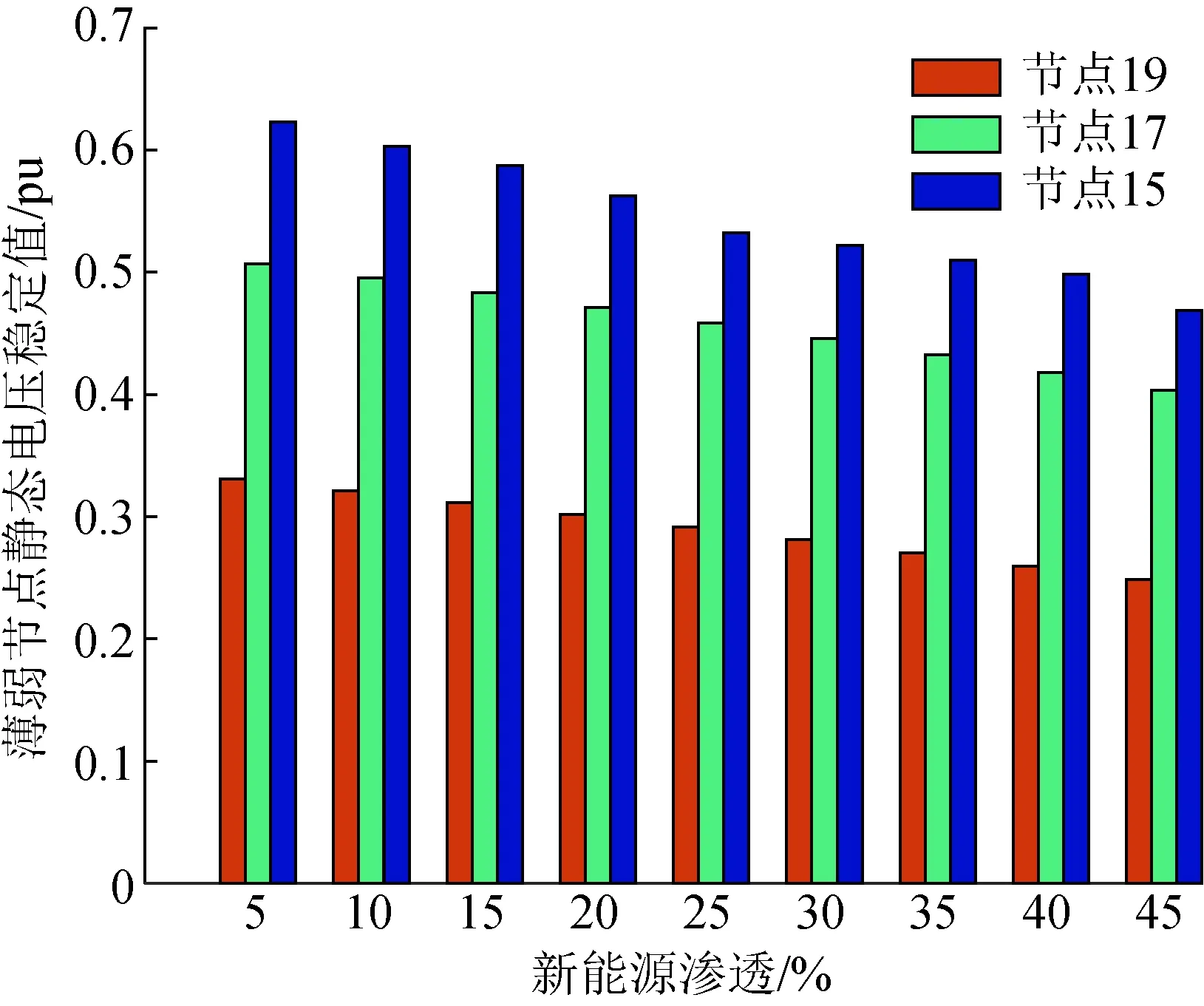
图8 新能源渗透率增长过程中薄弱节点的静态电压稳定值Fig.8 Static voltage stability of weak nodes in the process of new energy penetration growth

4.2 DSSC相较于SSSC的效果对比

DSSC作为分布式柔性交流输电装置的一个代表性设备,与静态同步串联补偿器(static synchronous series compensater, SSSC)为代表的大容量FACTS设备以及传统FACTS设备相比在结构方面更加简洁,更适合大规模安装解决电网整体潮流问题。图9是系统配置FACTS设备对系统静态电压稳定性提升效果对比,其中包括DSSC、传统FACTS和SSSC 等设备对静态电压改善的效果。分析可知:伴随着新能源渗透率的增加,系统静态电压稳定性呈下降趋势。相比于无FACTS装置的系统来说,当系统加入DSSC 装置后平均静态电压稳定指标提升0.152 5,系统加入传统FACTS设备后平均静态电压稳定指标提升0.120 1,系统加入SSSC 装置后平均静态电压稳定指标提升0.102 3,结果表明DSSC在改善系统静态电压稳定性方面更具优势。系统薄弱节点静态电压稳定性受到线路容量极限的限制,潮流过大会造成线路过载,DSSC灵活分布的特性可以有效解决多条线路潮流过载的问题,进一步提升系统的安全稳定性。

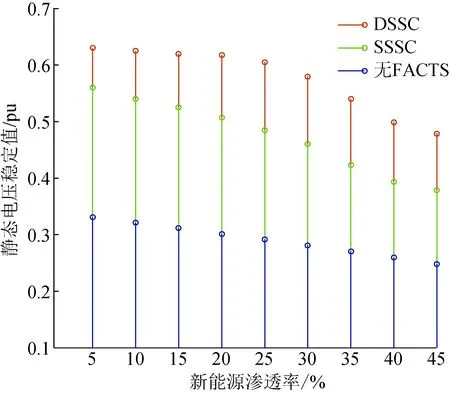
图9 配置FACTS设备对系统静态电压稳定性提升效果Fig.9 Improving the static voltage stability of the system by configuring FACTS equipment

4.3 DSSC安装位置和容量的影响

由图8可得系统薄弱节点为节点19,本文以节点19处接入DSSC的方案为基础,研究分析在不同薄弱节点处以及不同位置安装DSSC后系统的静态电压稳定结果,表1为不同配置地点的结果对比。

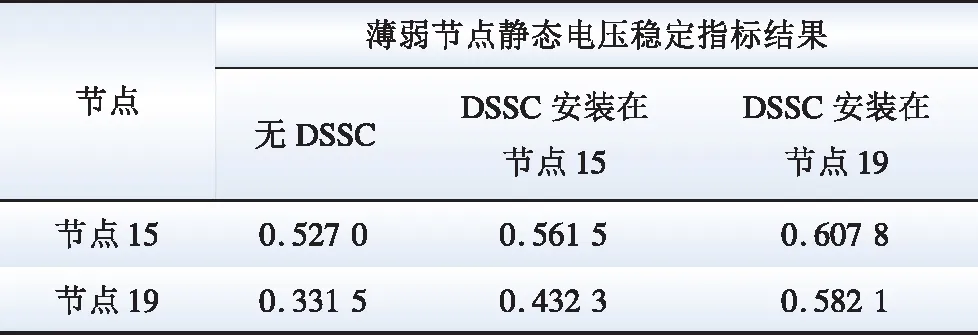
表1 不同位置下安装DSSC对薄弱节点静态电压稳定指标的提升Table 1 Improvement of static voltage stability index of weak nodes by installing DSSC in different positions

分析表1中系统静态电压稳定指标结果可得:无论是否接入新能源,DSSC均能提升电网的静态电压稳定性。将容量为70 MVA的DSSC配置在节点19处后,经分析可得线路16-19阻塞处潮流减小,且由线路16-19 组成的送端断面功率逐渐减小,系统静态电压稳定指标值相应提升。当系统在最薄弱节点19处安装DSSC对整体电压稳定性的改善更加明显,μVSI值提升了0.111 3。DSSC安装在薄弱节点15处μVSI值提升了0.049 9,结果表明DSSC对潮流的控制能力与接入薄弱节点位置的距离成正相关,距离薄弱节点越近DSSC装置调节支路潮流的能力越强,同时可增强新能源电网运行时的安全性与经济性。

表2为安装不同容量DSSC薄弱节点静态电压稳定性的变化情况。由表2分析可以得出:随着配置在系统薄弱节点处单个DSSC设备容量的增加,由系统重载线路16-19组成的送端断面功率逐渐减小,静态电压稳定值μVSI逐渐提升。当DSSC的安装容量达到11.55 MVA时,相比于不安装DSSC时静态电压稳定值μVSI提升了0.120 6。系统在薄弱节点处增大接入的DSSC设备容量,将会提升阻塞支路潮流控制能力,DSSC利用等效功率注入法将阻塞线路处潮流转移至其余相对空闲输电通道,优化整体潮流分布从而提升电网整体的安全稳定性。

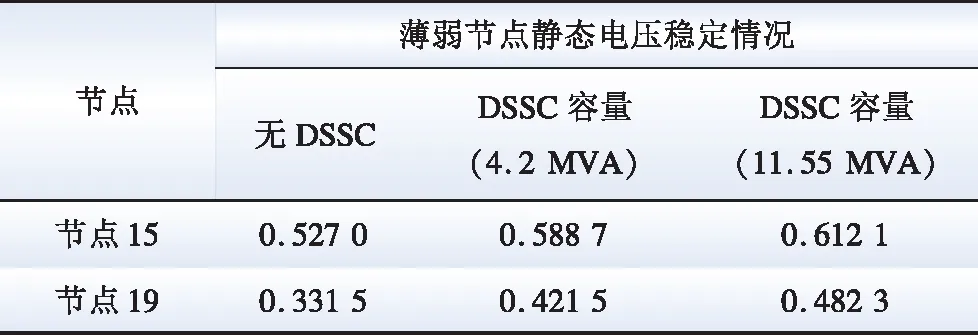
表2 安装不同容量DSSC薄弱节点静态电压稳定性的变化Table 2 The change of static voltage stability of DSSC weak nodes with different capacities

5 结 论

本文分析了DSSC对高渗透率新能源电网系统静态电压稳定性的影响,从提高系统静态电压稳定性方面评估DSSC发挥的控制潮流效能。将DSSC应用于改善新能源电网下的静态电压稳定性,提出基于DSSC等效功率注入模型的潮流计算方程,并基于潮流计算方程提出反映系统静态电压稳定的效能评估指标,计算分析接入不同容量新能源并网后对系统静态电压的影响以及DSSC对改善新能源并网静态电压安全稳定性的影响,结论如下:

1)高渗透率新能源并入电网后系统静态电压稳定性下降,DSSC通过注入功率的方式调节薄弱节点电压,有效提升新能源电网的安全稳定性。

2)相较于应用SSSC改善系统静态电压稳定性,在实际电网复杂的运行环境下安装DSSC更具适应性,能够更好提升新能源并网后系统的安全稳定性。

3)DSSC对潮流的控制能力与接入薄弱节点位置的距离成正相关,距离薄弱节点越近DSSC装置调节支路潮流的能力越强,同时安装DSSC在薄弱节点处可有效降低扩建输电设备的投资,提升新能源并网运行时的安全性与经济性。