柔性整流罩结构刚度优化设计研究
2023-09-27王桂娇颜世博王卓群
王桂娇,郭 葳,颜世博,芮 兴,王卓群
(1.北京宇航系统工程研究所,北京,100076;2.中国运载火箭技术研究院,北京,100076;3.北京航空航天大学,北京,100191)
0 引言
整流罩结构是运载火箭的重要组成部分,可为有效载荷提供良好的力热环境。当运载火箭到达预定轨道后,整流罩与运载火箭完成分离解锁,坠入大气层。由于整流罩半罩的结构尺寸通常较大,周向刚度低,再入大气层时,受气动阻力及自身动特性影响,会发生大幅度的低频响应,引起结构发生不同程度的解体,扩大了火箭残骸的落区范围,给地面疏散保障工作带来诸多困难。随着运载火箭发射密度的增大,这一问题变得尤为突出,为有效控制整流罩残骸落区范围,需要对整流罩半罩开展动刚度优化设计,通过降低整流罩再入过程的动响应,来实现整流罩半罩的完整降落。
结构动刚度优化设计方法主要有动特性优化和动响应优化两大类。其中动特性优化是通过调整结构参数来改变结构的频率及振型,使结构避免与外界激励产生谐振;动响应优化是对给定激励下的结构响应特性进行优化设计[1]。整流罩半罩以一定的初速度分离后,坠入大气层,承受的气动载荷与整流罩半罩的再入姿态和变形模式强耦合[2],且实时变化,很难对非定常的气动载荷进行分析,也就无法实现对整流罩结构的动响应进行有效评估,因此,本文将采用动特性优化方法对整流罩结构刚度开展优化设计。
为得到整流罩半罩的结构动力学特性,国内外学者通过有限元仿真和地面试验验证开展了大量研究。Bertram[3]通过扩充的模态鉴定试验验证了阿里安4半整流罩的数学模型,并研究了有限元分析中几何非线性对整流罩动特性的影响;朱春艳等[4]通过三点悬挂、四点悬挂和置于海绵垫的方式模拟整流罩的自由边界条件,开展了地面模态试验,并结合有限元分析技术对非金属夹层整流罩半罩的动力学特性开展研究;赵雪尧等[5]对大型复合材料整流罩全罩开展地面随机振动仿真,并对影响大型复合材料整流罩全罩模态特性的参数影响规律进行研究。
整流罩半罩再入大气层时,处于自由状态,受力模式和振动形式复杂多变,难以通过地面试验和理论计算进行有效模拟和评估,本文将采用有限元分析方法对非约束状态下的整流罩半罩开展动刚度优化设计,通过提高结构固有频率的方式,达到降低结构动响应的目的。
1 多自由度系统模态分析理论
多自由度(Multiple Degree of Freedom,MDOF)系统的运动方程为
式中M为n阶系统的质量矩阵;C为n阶系统的阻尼矩阵;K为n阶系统的刚度矩阵;x为n阶位移响应向量;F(t)为n阶激励力向量。
假设系统为无阻尼结构自由振动系统,即C=0,F(t)=0,则式(1)解的形式为
将C=0,F(t)=0和式(2)代入式(1)可得:
式中φ为n阶振型的特征向量(主振型);ω为n阶振型的振动频率(固有频率);t0为初始时刻。
通过模态分析(即特征值求解),可以得到系统的频率和模态振型,由式(3)可以看出:
a)结构的固有频率和振型主要取决于结构的质量分布和刚度分布,同时还与结构的阻尼、外激励有关;
b)结构的固有频率与结构刚度呈正相关,与结构质量呈负相关,因此在对结构进行动特性优化时,要平衡好刚度和质量的关系。
2 有限元仿真
模态分析是进行结构动力学设计和方案验证的重要手段[6-8],在运载火箭的结构设计中占据十分重要的地位,通过模态分析,可以获得结构的模态频率和振型。本文基于有限元分析软件Abaqus线性摄动分析模块对整流罩半罩结构开展自由边界下的模态特性分析。
2.1 有限元建模
整流罩半罩结构有限元模型如图1所示,模型从上到下依次为端头帽、锥段、前后柱段,除端头帽外,其余部段均为蒙皮桁条式半硬壳结构。

图1 整流罩半罩有限元模型Fig.1 Finite element model of half-fairing
整流罩锥段和前后柱段由蒙皮、桁条、环框和局部加强结构组成,其中蒙皮与桁条、环框间连接面通过铆钉连接,端头帽与锥段、锥段与前柱段、前柱段与后柱段间端框连接面均通过密布螺栓连接。同时为满足仪器设备安装需求,整流罩内部还设计有局部安装支架,众多的铆钉、连接螺栓和小支架等细节特征导致整流罩结构建模极其复杂,因此,本文在真实模拟结构刚度的前提下,忽略对结构刚度影响微小的结构件,并将铆钉及端面连接螺栓简化设置为tie连接。进行网格划分时,蒙皮、桁条及环框采用完全积分壳单元S4离散,端头帽及加强角盒等采用非协调实体单元C3D8I离散。本建模方法已多次应用在长征二号丙、长征三号系列等运载火箭的整流罩有限元分析中,均通过了地面试验考核,验证了方法的正确性。
2.2 模态分析结果
一般情况下,结构更容易在低频段受到外界影响,而且低阶振型对结构造成的影响远比高阶振型严重[9]。本文提取整流罩半罩20 Hz 以内的非刚体自由模态,固有频率及模态振型汇总见表1,模态振型图如图2所示。

表1 前4阶固有频率及模态振型汇总表Tab.1 First 4 rank vibration modes of half-fairing

图2 整流罩半罩前4阶模态Fig.2 First 4 rank vibration modes of half-fairing
由图2可以看出:
a)整流罩半罩模态以扭转模态和呼吸模态为主;
b)由于整流罩半罩为半开放式结构,一阶振型的抗扭刚度低,使结构发生了扭转变形;
c)二阶、三阶模态振型反映出整流罩半罩的周向刚度低,使结构发生了沿箭体径向的振动;
d)结构的刚度薄弱位置主要分布在部段对接面处:端头帽-锥段、锥段-前柱段和前柱段-后柱段,其中,锥-柱连接面为刚度最薄弱的位置。
通过对比整流罩半罩再入视频,发现整流罩结构再入过程中发生了大幅低频振动,振型以扭转模态和呼吸模态为主,与有限元仿真的低阶模态一致。整流罩半罩残骸的锥-柱段对接处、柱段中心线等刚度薄弱位置出现了不同程度的断裂破坏,破坏位置与有限元仿真的模态高应力区位置一致,也验证了有限元模型的准确性。
3 整流罩动特性优化设计
本文在整流罩半罩结构质量不增加的约束条件下,以提高整流罩半罩一阶扭转频率作为动特性优化的目标,开展结构参数影响规律研究和刚度优化,探索提升整流罩半罩动刚度的有效措施。
3.1 结构参数影响规律研究
为研究结构参数对整流罩半罩动特性的影响,本文首先建立了简化的整流罩半罩参数化模型,并以该简化模型为基准,研究桁条尺寸、桁条数量、环框尺寸及环框数量等结构参数对整流罩频率和模态振型的影响。
3.1.1 桁条高度影响规律
保持整流罩半罩除桁条以外结构的尺寸及位置不变,通过改变桁条高度,研究桁条高度对整流罩动特性的影响规律。
图3为整流罩半罩一级扭转模态和一阶呼吸模态频率随桁条高度的变化曲线。
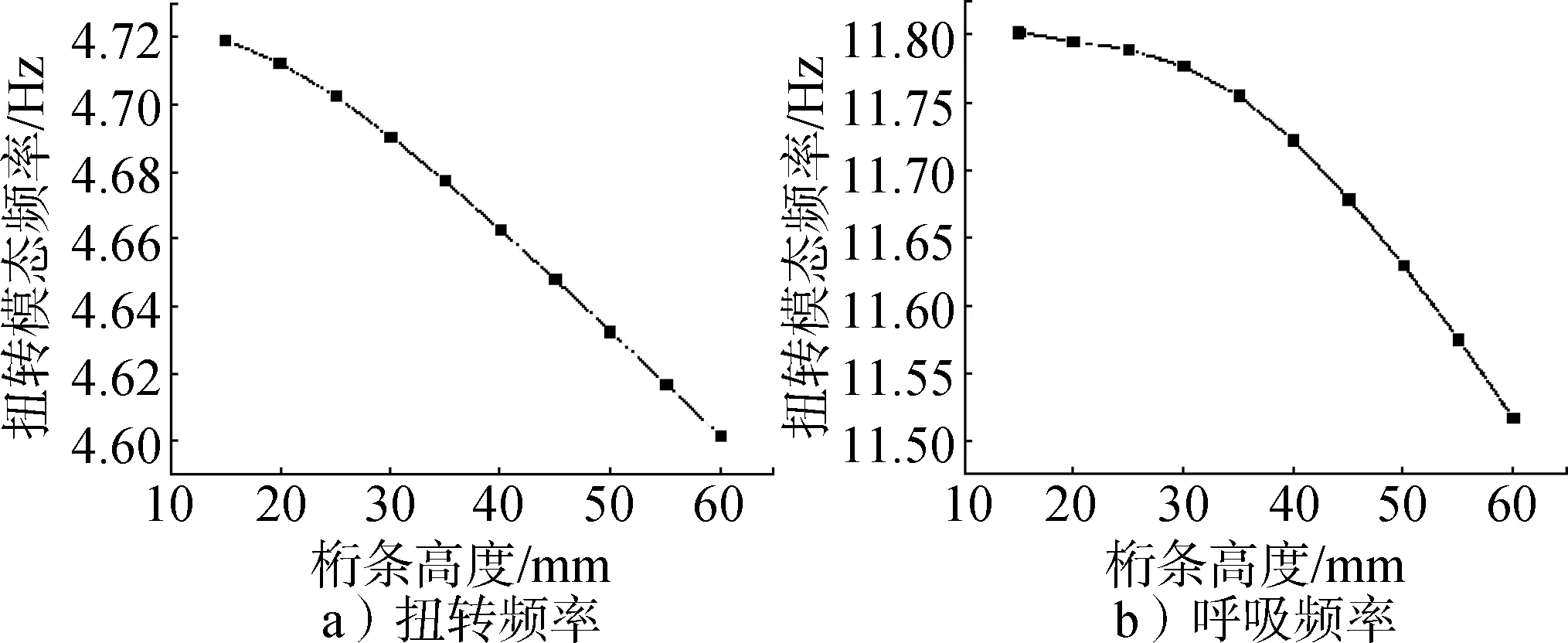
图3 桁条高度-结构模态频率曲线Fig.3 Comparison of strings height
根据图3曲线可以看出:
a)随着桁条高度的增加,结构的一阶扭转和一阶呼吸模态频率都逐渐下降;
b)桁条高度的增加对结构刚度的影响有限,然而增大的结构质量会导致频率的降低;
c)在控制结构质量不增加的条件下提高结构频率,需要在满足结构强度的情况下选用较小的桁条高度。
3.1.2 桁条数量影响规律
保持整流罩半罩除桁条以外结构的尺寸及位置不变,通过改变桁条数量,研究桁条数量对整流罩半罩的结构动特性影响规律。
整流罩半罩扭转模态和呼吸模态频率随桁条数量变化的曲线见图4,根据曲线可以看出:桁条数量对结构频率的影响与桁条高度的影响类似,随着桁条数量的增加,结构的一阶扭转频率和一阶呼吸频率都逐渐下降。

图4 桁条数量-结构模态频率曲线Fig.4 Comparison of strings number
3.1.3 环框尺寸影响规律
整流罩半罩的周向刚度是影响结构呼吸模态的主要因素,提升环框刚度有助于提升结构的周向刚度。
为研究环框尺寸对整流罩半罩动特性的影响,本文保持整流罩半罩环框以外的结构尺寸、位置及环框对称面位置与初始模型一致,研究前柱段、后柱段环框高度和宽度对结构频率的影响。
图5为环框高度和宽度对结构一阶扭转频率和一阶呼吸频率的影响分布。

图5 环框参数-结构模态频率分布Fig.5 Comparison of circular frame parameter
由图5可以看出:
a)随着环框宽度的增加,整流罩半罩的一阶扭转频率呈单调上升趋势;
b)环框宽度对整流罩半罩的一阶呼吸频率影响不明显;
c)环框宽度较小时,随着环框高度的增加,整流罩半罩的一阶扭转频率单调增加,在环框宽度为200 mm,高度为90 mm时取得极值;
d)随着环框高度的增加,整流罩半罩一阶呼吸模态频率显著提高,在环框高度大于125 mm 之后逐渐趋于稳定。
图6为环框参数对整流罩半罩结构质量的影响分布,由图6可以看出,环框高度及宽度的增加均会使结构重量呈线性增加。
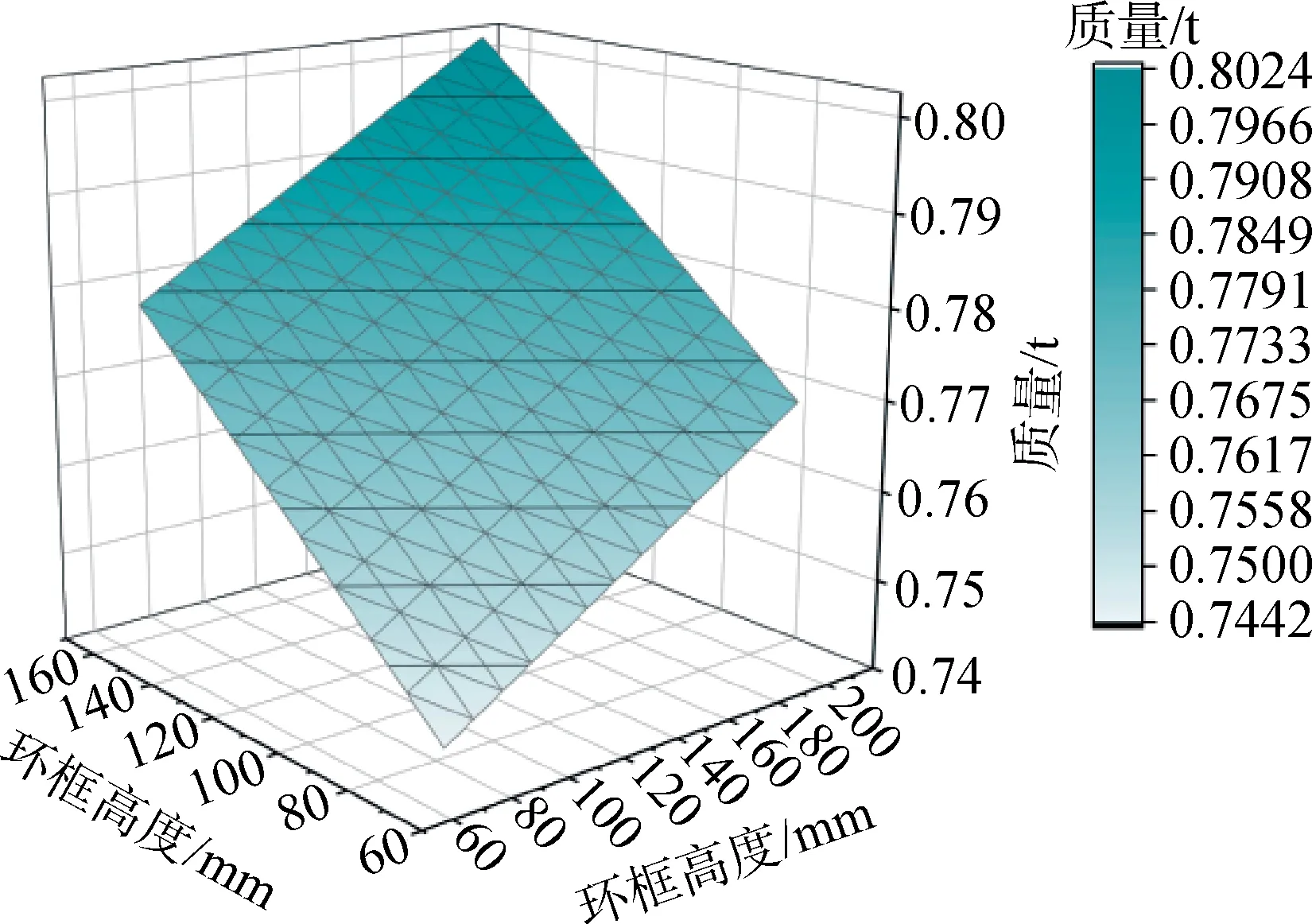
图6 环框参数-结构质量Fig.6 Structure weight of different circular frame
为提升运载火箭的运输能力,箭体结构需要尽可能轻量化,为得到不同结构质量下对应的最优解,在频率分布图中增加了不同结构质量对应的控制平面(图7中红色平面即等重量参考面),控制平面与曲面交线的最高点即为保持总重量不变情况下的最优方案。

图7 结构-频率分布Fig.7 Frequency of different structural weight
由图7 可以看出,保持结构总质量不变的条件下,环框宽度对整流罩半罩一阶扭转频率的影响更大,选择较大的宽度,较小的高度,可以实现在结构质量不变的情况下得到更高的结构频率。
3.1.4 环框数量影响规律
保持整流罩半罩的前、后柱段的环框总数量不变,研究环框分布对整流罩半罩一阶扭转频率和一阶呼吸频率的影响,图8 为环框布局-频率分布,根据图8可以看出:
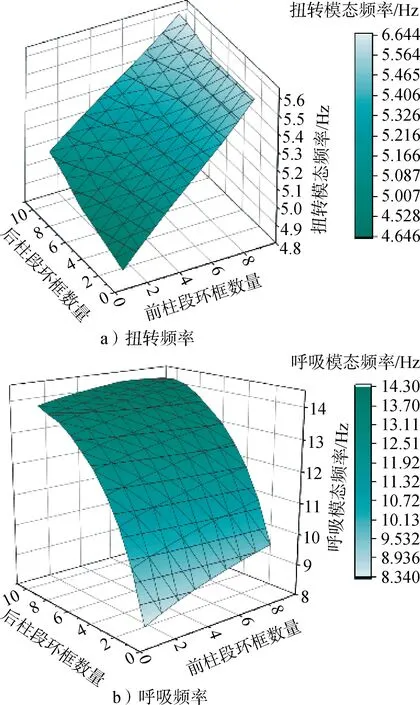
图8 环框布局-频率分布Fig.8 Comparison of circular frame distribution
a)前柱段和后柱段环框数量的增加都会引起一阶扭转频率的提高,其中前柱段环框数量M对扭转模态频率的影响更为显著;
b)在保持质量不变的情况下,前柱段的环框数量越多,结构的一阶扭转频率越高,但是呼吸频率会降低。
根据上述分析,可得以下结论:
a)桁条对于提升整流罩半罩的扭转频率和呼吸频率的作用有限,但是结构质量的增加会导致频率降低;
b)考虑到桁条在结构承载中的作用,在进行整流罩半罩动特性优化时,可在保证结构满足强度要求的前提下,尽量选取较小的桁条尺寸和数量;
c)环框数量和尺寸的增加都会提高结构的扭转频率,因此,对整流罩半罩进行动特性设计时,可在型材库中选择高度和宽度更大的材料以提高结构的扭转频率,在保持结构质量不增加的情况下,可以选择更大的环框宽度,适当降低环框高度,以实现结构扭转频率的提高;
d)前、后柱段环向抗弯刚度增加,都会提高结构的扭转频率,相比后柱段,前柱段的抗弯刚度对于扭转模态的频率影响更为显著;
e)整流罩半罩的一阶呼吸频率随柱段环框高度的增加显著提高,在环框高度大于125 mm 之后逐渐趋于稳定,柱段环框宽度对整流罩半罩的一阶呼吸频率影响不明显。
3.2 整流罩刚度优化
观察整流罩半罩的再入视频,大幅低频振动响应发生在一阶扭转频率附近,所以为控制整流罩半罩的低频振动响应,本文在3.1 节研究的基础上,对整流罩半罩原始方案的详细模型开展局部刚度优化,通过提高整流罩半罩的一阶扭转频率,降低整流罩结构的动响应。
优化原则:a)不改动原始整流罩结构方案;b)不影响整流罩锥段以下结构的内部空间包络;c)加强结构件尽可能轻质化。在此原则下,本文研究了以下 4种加强方案对整流罩半罩动特性的影响规律。优化结构方案及内部加强结构件如图9~10所示。

图9 优化方案示意Fig.9 Optimization schemes
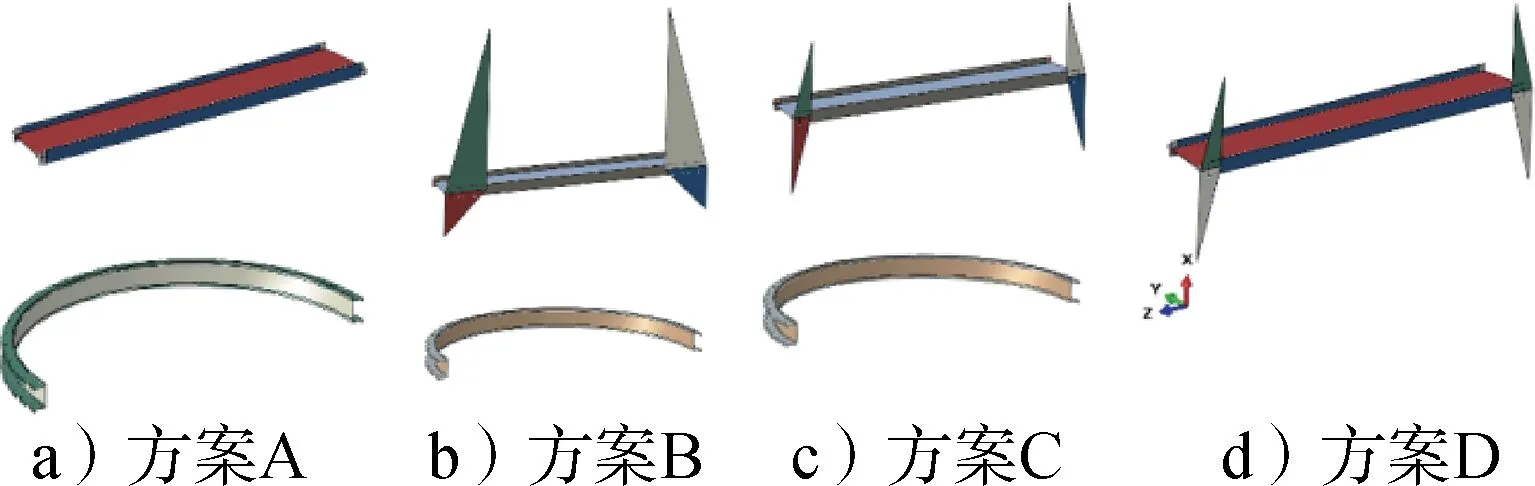
图10 内部加强结构Fig.10 Internal reinforcement structure
四种加强方案简述如下:
方案A:在锥-柱对接面施加横梁,在柱-柱对接面施加环形“C”形框;
方案B:在方案A的基础上,上整流罩锥段下端框及前柱段上端框处施加三角形壁板;
方案C:对方案B三角形壁板进行参数化优化;
方案D:在方案C的基础上取消柱-柱对接面处的“C”形框。
以上4种优化方案的一阶扭转和一阶呼吸频率分析结果汇总见表2,模态振型图分别见图11~14。根据分析结果可以得出以下结论:a)整流罩半罩的锥-柱连接面是结构的刚度突变区,也是影响结构固有频率的关键部位;b)在锥-柱连接面外缘设置纵向加强结构,可为连接面处提供额外的抗弯刚度,使整流罩半罩的一阶扭转频率提升50%以上;c)增加柱段环框刚度,可提升整流罩半罩的一阶扭转模态和一阶呼吸模态。

表2 分析结果汇总表Tab.2 Summary of analysis

图11 方案A模态振型Fig.11 Modal shape of scheme A

图12 方案B模态振型Fig.12 Modal shape of scheme B

图13 方案C模态振型Fig.13 Modal shape of scheme C
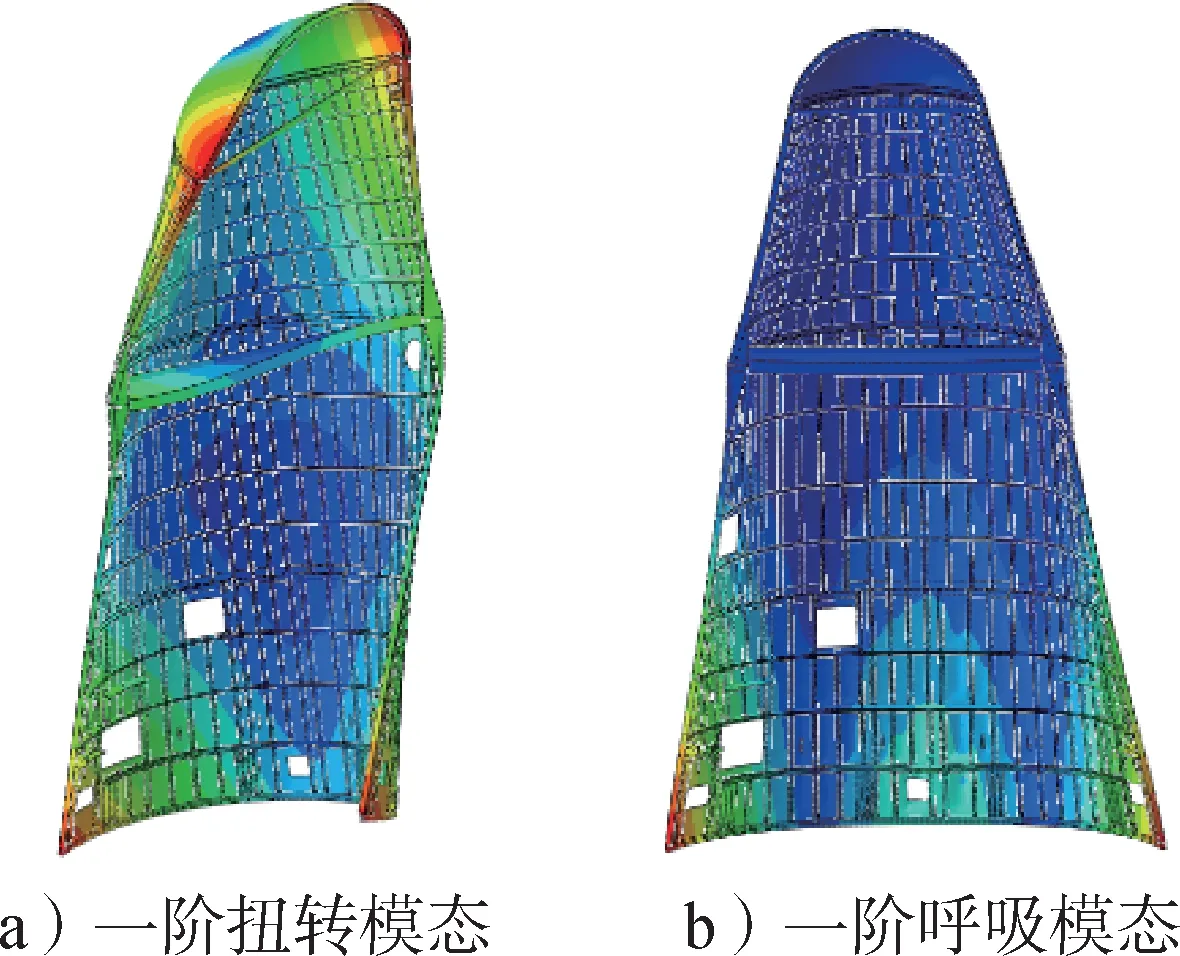
图14 方案D模态振型Fig.14 Modal shape of scheme D
4 结论
a)整流罩半罩为开放式半硬壳结构,抗扭刚度低,再入大气层时,大幅的低频振动响应是整流罩半罩解体的主要原因,提高结构固有频率是降低整流罩半罩动响应的有效途径;
b)结构的模态频率与结构刚度正相关,与结构质量负相关,通过调整结构参数来提高模态参数时,要协调好结构刚度与质量的关系;
c)桁条数量及高度的增加对提高整流罩半罩的扭转频率和呼吸频率作用有限,结构质量的增加反而会导致整流罩刚度降低,可采取增加环框宽度,并适当降低环框高度的方式提升整流罩半罩的固有频率;
d)整流罩半罩的锥-柱连接面是结构的刚度突变区,也是影响结构固有频率的关键部位,通过提高该部位的局部抗弯刚度,可以实现以较小的结构质量,显著提升整流罩半罩的固有频率。
