运载火箭起飞漂移量主动控制方法研究

陈士强，王紫扬，陈佳晔，张普卓，赵永志

（北京宇航系统工程研究所，北京，100076）

0 引言

运载火箭起飞漂移量发生在火箭离开发射台到火箭尾部离开发射塔顶端的阶段，即起飞段。火箭脱离发射台约束后在外干扰和内干扰作用下发动机摇摆控制将导致横向质心运动和绕质心运动，箭体头部、尾部以及其他凸起位置将偏离原竖直上升方向，箭塔间隙发生变化，因此在火箭上升过程中存在与发射塔设施碰撞的风险。为避免箭塔安全间隙不足的问题，需要对起飞段火箭横向漂移量进行计算评估以及控制优化。

新研火箭在方案论证阶段开展起飞漂移量计算供地面发射系统开展设计使用，横向漂移量制约了脐带塔及发射塔需预留的箭塔安全间隙，预留安全间隙大小直接决定了地面发射系统设计规模和经济成本，因此需要采取主动控制策略降低起飞段横向漂移量。现役执行高密度发射任务型号（例如CZ-2C 系列火箭）正在开展一系列低成本及简化发射设施和射前流程的设计改进［1］，例如电气一体化设计、取消垂调设备等。相关单机的减配和射前流程的优化将在一定程度上影响垂调精度，垂调精度的降低可能导致火箭初始姿态偏差增大、惯组惯性基准和火箭理论箭体坐标系以及火箭一级发动机机架水平面间的不水平度增加，一系列偏差的提高将导致起飞段漂移量增加。对于成熟型号，发射场设施难以调整，仅能通过优化控制方案降低起飞漂移量。综上，无论新研运载火箭方案论证或现役火箭相关技术状态更改均对起飞段漂移量主动控制技术研究提出迫切需求。

国外运载器设计关于起飞漂移量的研究起步较早。在美国大力神3C 火箭研制过程中发现在二月、三月有较大的概率火箭不能发射，采用一定的偏航程序角控制后，能够保证99%的发射率［2］。大力神3C的飞行路径干涉主要表现为火箭与摆杆包络之间的干涉。在对大力神3C的起飞段动力学研究中包含8个独立随机变量，比如：推力线偏斜、质心横移、敏感器件误差等。报告指出解决飞行路径干涉的办法有两个：采用俯仰程序控制；降低设计用地面风速的保守性。阿里安5研制过程中，按照各项干扰独立随机变量考虑其统计分布，采用蒙特卡洛打靶法计算起飞漂移量，进而确定起飞段箭体外包络［3］。肯尼迪航天中心结构分析实验室的David Chesnutt 开发了一种起飞段箭塔干涉仿真分析工具（Umbilical Clearance Tool，UCT）［4］，用于仿真箭体起飞段的飞行过程，并自动分析火箭与塔架和摆杆的干涉情况。

随着新一代运载火箭的研制，对起飞漂移主动控制的需求愈加迫切。文献［5］描述了起飞段多约束漂移量控制问题。通过增益控制、滚动程序角补偿、提前起控时间等工程措施，解决了长征五号火箭起飞段漂移量控制难题。起飞漂移量主动控制措施主要分为两类：离线设计远离发射塔的飞行程序；在线闭环反馈控制。起飞段增加主动控制程序角属于一种离线开环控制方法，需要结合明确的箭塔方位关系开展程序角设计。目前中国暂无漂移量闭环主动控制方法研究。

本文针对运载火箭起飞漂移量闭环主动控制问题提出了3种无须增加设备、基于现有可获得信息增加反馈回路的漂移量主动控制方案：a）速度位置反馈控制；b）加速度反馈控制；c）推力矢量角反馈控制。3种方案均为在原PD控制基础上补充漂移量相关状态量反馈的思想，控制架构更改小，具有较高的工程应用前景。

1 起飞段火箭动力学模型

漂移量控制问题主要研究刚体运动，推进剂晃动和弹性运动对漂移量影响较小，因此在本文研究中忽略。采用标称轨迹展开的小偏差模型进行分析［6］。俯仰通道动力学方程如式（1）所示，偏航通道动力学方程如式（2）所示。

式中V为飞行速度；y，z分别为火箭质心法向和横向漂移量；φ，ψ分别为俯仰和偏航姿态角；α，β分别为攻角和侧滑角；θ，σ分别为弹道倾角和弹道偏角；δφ，δψ分别为俯仰和偏航通道控制摆角。动力学系数中k1为动力系数，k2为气动力系数，k3为控制力系数，b2为气动力矩系数，b3为控制力矩系数。方程右端，为合成结构干扰力系数，，为地面风干扰力系数，，为合成结构干扰力矩系数，为地面风干扰力矩系数，表征起飞段箭体起飞段受到的干扰力和力矩。

火箭尾部漂移量计算公式：

式中Iy，Iz，I分别为箭体尾部法向、横向及周向漂移量；l1为火箭尾喷口距离质心距离。

传统PD控制方案三通道控制摆角：

式中a0，a1分别为姿态回路的角偏差增益和角速度增益。俯仰和偏航通道模型一致，后文以俯仰通道为对象进行说明，省略通道角标。

2 漂移量控制问题描述

起飞漂移如图1所示。

图1 起飞漂移描述Fig.1 Lift-off drift schematic

造成火箭飞离发射台面和飞离发射塔过程漂移量的影响主要诱因分类如下。

a）内部干扰：主要指由质量特性偏差、发动机相关偏差等火箭系统内偏差造成的干扰，也可称为结构干扰。

b）外部干扰：主要为地面风干扰、塔架遮挡效应等。

c）初始条件偏差：包括风载导致的初始姿态偏差，初始姿态角速度，惯组安装偏差及垂调偏差导致的惯性基准偏差，一级发动机机架不水平度等。

结合现役火箭漂移量计算结果，地面风干扰和系统结构干扰对出塔漂移量影响最为显著，初始姿态偏差会导致飞离发射台面产生较大的初始尾部横移。

初始姿态偏差造成漂移量主要为系统响应姿态偏差过程中超调造成。出塔漂移量主要由火箭推力在横向分量造成，推力矢量偏移基准面分量主要由箭体姿态偏斜和发动机摆角造成。姿控系统对初始偏差的瞬态响应造成的漂移控制上使用的硬件调零装置或初始姿态补偿的软调零手段均有较好的应用效果。而火箭飞离发射台面到出塔过程的漂移量大小主要由系统稳态误差主导，因此优化起飞段全程漂移量需要通过控制方案改进的手段实现。

起飞漂移量控制的本质问题是在满足系统稳定性的条件下，优化控制器设计使系统对初值扰动和系统干扰的响应速度提高，稳态误差降低。下面先以传统控制方案分析起飞漂移量控制问题。对于传统PD 控制三通道控制摆角：

可以得到系统的闭环特征方程：

在分析干扰对漂移量的影响时忽略绕心运动方程动态项和微分控制项，得到简化分析方程：

起飞段箭体动力学特性变化较小，系统外干扰时变，由此可以得到：

方程的解

由式（11）可见增大P(t)或减小Q(t)对于减小漂移量y都是有利的。根据式（9）和（10），增大a0可以使Q(t)减小，但不能使P(t)显著增大甚至减小，因此增大a0的效果是有限的。由式（6）系统的闭环特征方程可见系统存在一个位于零点的根，系统处于临界稳定状态，通过调整a0，a1可以控制横向速度在干扰作用下稳定收敛至稳态，但速度积分项不能收敛。

工程设计中，当火箭构型和飞行剖面确定后，根据系统截频和姿态响应阻尼需求以及高频稳定裕度需求，姿控系统主通路a0，a1基本确定，可调节控制参数少、可调范围有限，且起飞段飞行时间短，一般不会牺牲姿态稳定裕度用以减小起飞漂移量，所以横法向位置控制为开环状态。

由此可得，为减小起飞漂移量，需要补充漂移量反馈控制回路，优化控制策略，增加漂移量直接位置反馈或加快漂移速度收敛。漂移量主动控制设计原则为在满足主通路稳定裕度的基础上最大化漂移量抑制效果。

3 起飞漂移量主动控制方法研究

3.1 速度位置反馈控制策略

起飞段速度位置反馈控制策略为在原有PD 控制基础上补充发射系位置漂移和速度漂移反馈控制回路，如图2所示。

图2 速度位置反馈控制结构Fig.2 Velocity and position feedback control

指令摆角形式为

式中y，分别为法向漂移量和漂移速度；ag0，ag1分别为火箭质心运动位置和速度漂移增益系数。

将控制方程带入简化的动力学方程后，得到系统闭环特征方程：

根据主通路刚晃弹稳定控制需求设计主通路角偏差增益a0和角速度增益a1。在保证主通路稳定性的基础上设计漂移量控制回路参数，固化PD 控制增益a0，a1，分析a0，a1可调范围。为简化分析取ag0=ag1，随速度位置反馈增益增大系统特征方程根的变化情况如图3所示。

图3 速度位置反馈控制策略系统闭环特征根分布Fig.3 Closed loop characteristic equation roots of velocity and position feedback control

经分析，为满足系统稳定性要求，速度位置反馈回路增益需要满足ag0，ag1＜0.012。在闭环特征方程无正根的基础上，系统需要保证一定的稳定裕度，以适应系统参数摄动。取不同漂移量控制增益情况下系统开环尼科尔斯图见图4。

图4 速度位置反馈控制系统开环尼科尔斯图Fig.4 Open loop Nichols figure of velocity and position feedback control

随着速度位置反馈增益增大，系统低频稳定裕度降低。经分析，速度位置反馈回路增益取ag0=ag1=0.01 时系统裕度充足，进一步提高导引增益将导致系统相位裕度不足。

3.2 基于加速度信息的漂移量主动控制策略

基于加速度信息的起飞漂移量主动控制方案为增加发射系箭体加速度即相对塔架的漂移加速度反馈回路，如图5所示。

图5 加速度反馈控制结构Fig.5 Lateral acceleration feedback control

控制器设计：

式中ag为火箭质心运动加速度增益系数。起飞段加速度反馈漂移量主动控制和大风区主动减载控制不同，漂移量控制反馈量为发射系下的横、法向相对加速度，而大风区减载控制反馈为体系下的横、法向视加速度。

将控制方程带入动力学方程中可以得到增加加速度反馈回路后特征方程：

固定PD 控制增益，ag由0 变化至0.1 系统非零闭环特征根的变化情况如图6所示。

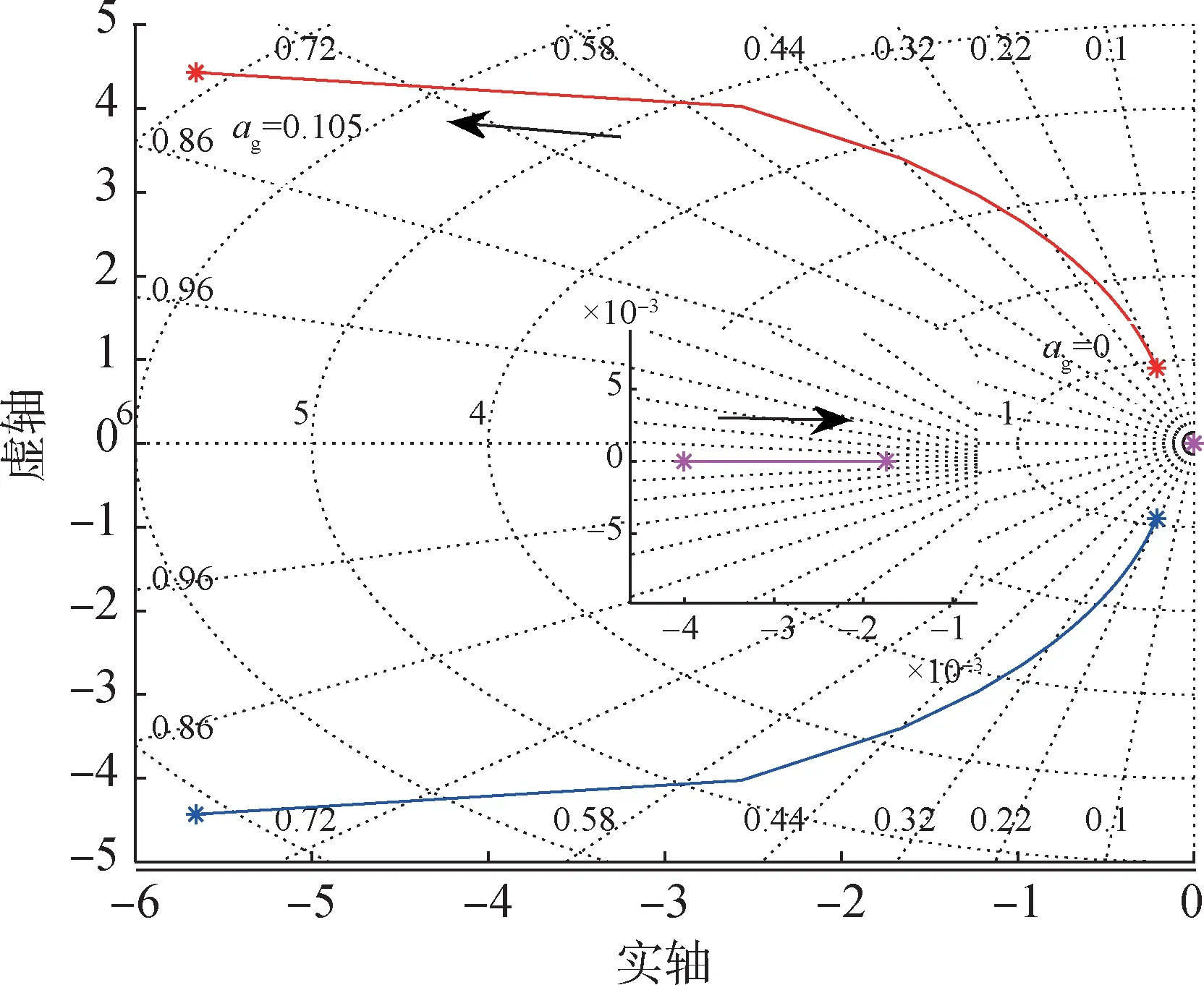
图6 系统闭环根轨迹Fig.6 Closed loop characteristic equation roots of lateral acceleration feedback control

根据简化推导的闭环特征方程根典型秒点下除零根外其他根轨迹变化图可知：系统有3 个主导极点，为一对共轭复数极点和一个实极点，其中实极点十分接近虚轴。随着ag变大，系统的3个极点逐渐远离虚轴，系统响应速度变快。满足系统闭环特征根都在左半平面的增益需要满足ag≤0.11。取不同增益条件下系统尼科尔斯图如图7所示。

图7 加速度反馈控制开环尼科尔斯图Fig.7 Open loop Nichols figure of acceleration feedback control

增加加速度反馈对低频段幅频特性影响较小。随着ag的提高刚体截止频率提高，系统响应速度变快，但相位裕度损失，ag继续增加系统不稳定，兼顾漂移量控制效果的同时需要保证系统足够的稳定裕度，综合考虑取ag=0.05。

3.3 基于推力矢量角补偿的漂移量主动控制策略

推力矢量的横法向分量是造成起飞漂移的直接原因。基于推力矢量偏斜角的补偿策略，为获得发动机推力矢量与发射系XOY和YOZ的夹角反馈至控制系统进行闭环控制，进而减小漂移量推力矢量角反馈控制如图8所示。结合简化动力学模型，暂不考虑发动机复杂模型，推力矢量和XOY和YOZ平面的夹角可以简化：

图8 推力矢量角反馈控制Fig.8 Thrust vector angle feedback control

将推力矢量角补偿至控制方程中得到控制摆角：

图9 为考虑推力偏移角反馈控制后的开环频域图，其中由0变化至1。

图9 推力矢量角反馈开环尼科尔斯图Fig.9 Open loop Nichols figure of thrust vector angle feedback control

增加推力矢量角反馈低频影响同样较小。随着ag的提高截止频率提高，但因推力矢量反馈控制环节中存在延迟造成刚体相位裕度损失，ag增加到1 系统不稳定，在原PD 回路增加推力矢量反馈控制牺牲了一定的刚体控制裕度，因此在控制器设计优化漂移量控制效果的同时需要保证系统足够的稳定裕度，综合考虑取ag=0.9。

4 仿真验证

上文阐述的3种漂移量主动控制策略中，速度和位置反馈直接反映了横向漂移量，横向加速度反馈和推力矢量角反馈的量本质上均为推力的横向加速度分量。速度位置反馈可完全控制横向位移收敛至稳态，后两种仅能提高横向漂移速度的收敛性，实际上漂移位置属于临界稳定状态对应系统闭环特征根含一个零根。

基于某型火箭小偏差模型开展起飞段动力学仿真，验证上文中3种反馈控制对起飞漂移量主动控制的有效性。其中导引控制增益取ag0=0.01 rad/s，ag0=0.01 rad/（m·s-1），加速度计反馈增益取ag=0.05 rad/（m·s-2），推力矢量偏斜角反馈控制增益取ag=0.9，分别如图10～12所示。

图10 姿态角偏差Fig.10 Euler angle deviation

图11 Y向和Z向尾部漂移量Fig.11 Lift-off drift of Y/Z direction

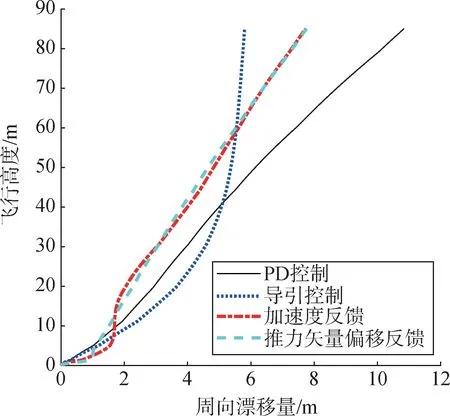
图12 合成漂移量Fig.12 Synthesized lift-off drift

经仿真，采用传统PD 控制无漂移量主动控制和采用不同主动控制策略出塔尾部漂移量统计见表1。

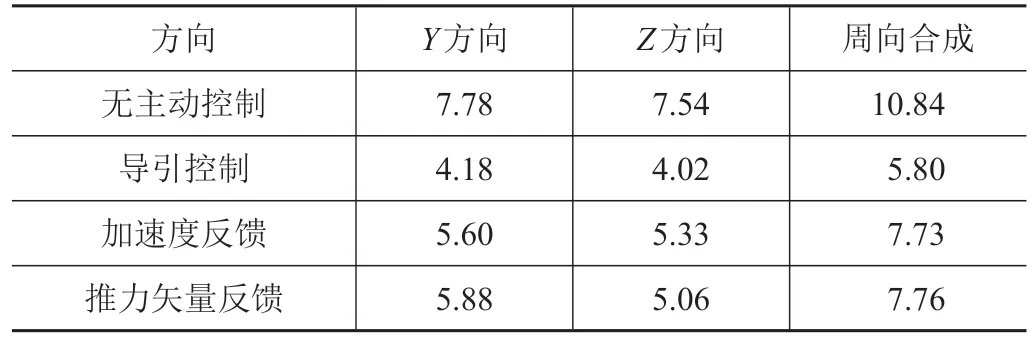
表1 漂移量仿真结果统计Tab.1 Relsults of take-off simulations

经仿真验证有以下结论：

a）采用速度位置反馈控制、加速度反馈控制、推力矢量控制3 种策略，在固化PD 控制增益情况下相对于漂移量主动控制合成漂移量可分别减小46%、29%、28%，均能起到较好的漂移量主动控制效果。

b）速度位置反馈控制对漂移位置直接反馈，横向位置回路稳定，漂移量控制效果最佳，角偏差有所增大，低频、幅频特性影响较大。

c）目前3 种不同策略在固化PD 控制增益情况下分析，工程应用中可通过各通路增益a0，a1，ag，校正网络联合优化来实现更优的漂移量控制效果。

d）3种控制策略中，方案一和方案二需要的质心加速度或速度和位置信息对于现有控制系统获取较为容易，方案三中的推力矢量角目前不具备直接输出条件，因此方案一和方案二工程推广可行度更高。

5 结束语

本文首先分析了起飞段漂移量控制的核心问题，并提出了3种具有工程应用前景的漂移量主动控制方案；其后，针对3种控制策略结合某型号火箭起飞段动力学方程及系数，分析漂移量控制增益取值对系统稳定性影响，约束系统主通道增益条件下设计在能够保证系统稳定性和足够稳定裕度的漂移量主动控制增益；最后，采用3种控制策略和对应设计控制增益仿真验证漂移量控制效果。经验证，采用增加速度位置反馈控制分支、漂移加速度反馈或推力矢量角反馈控制均能对起飞段漂移起到较好的抑制效果，且保证了系统具有足够的稳定裕度。