基于云服务器的公平多方隐私集合交集协议

张 静，田 贺，熊 坤，汤永利，杨 丽

（河南理工大学 软件学院，河南 焦作 454000）

0 引言

隐私集合交集（Private Set Intersection，PSI）协议是安全多方计算重要的组成部分，它允许持有各自集合的参与方在不泄露私有信息的前提下共同计算集合的交集［1-2］。PSI 技术是许多密码协议的基础模块，也被广泛应用于数据挖掘、人工智能和数据共享的安全领域，如商业广告精准投放［3］、共同好友推荐［4］、银行实名认证［5］、隐私保护的用户匹配［6］、刑事案件侦查［7］等。

近年来，云计算技术的逐步应用为不同用户之间的联合计算提供了便捷、高效的服务，因此许多研究者利用云服务器结合混淆布隆过滤器（Garbled Bloom Filter，GBF）、不经意传输（Oblivious Transfer，OT）等密码技术解决多方隐私信息交集计算问题。Inbar 等［8］基于GBF 和秘密共享提出了一种云外包多方的PSI 协议；Kavousi 等［9］基于不经意伪随机函数提出了云外包的多方PSI 协议——多方隐私集合交集协议（Multi-party PSI protocol，MPSI），对密钥进行秘密共享，有效避免了集合元素索引值泄露，同时使通信和计算复杂度仅取决于参与方集合元素的数量；Ben-Efraim 等［10］使用OT、GBF相结合在恶意模型下实现了多方PSI 协议——实用多方恶意安全私有集合交集PSImple；Debnath 等［11］利用布隆过滤器（Bloom Filter，BF）、同态加密、零知识证明-数据签名结合技术设计了一种抵抗恶意敌手的云外包PSI，实现了标准模型下的安全，且取得了较低的线性复杂度；Kano 等［12］结合BF（Bloom Filter）和云服务器提出一种新的多方PSI 计算方法——隐私集合交集求和（Private Intersection Sum，PI-Sum），一定程度上规避了BF 的错误概率，提高了计算的准确性；Debnath 等［13］提出一种恶意安全的不经意伪随机函数来维护PSI 协议的公平性，并使用同态加密算法来保护数据隐私；之后Debnath 等［14］又在文献［13］的基础上提出了基于素数阶群的PSI 协议，协议使用同态加密算法来保证数据的安全性，并使用半诚实的云服务器来实现参与者之间的公平性。然而，文献［8］中的协议在执行过程中，参与方之间的交互会造成集合元素索引值泄露。在文献［9-12］中，只有指定参与方得到交集的结果，这种情况对于未指定的参与方并不公平。文献［13-14］中实现了公平的PSI 计算，但是使用同态加密来保护数据隐私导致协议计算复杂度较高。

受上述文献的启发，本文在云服务器辅助下基于GBF 与OT 提出了一种公平多方隐私集合交集协议，记为ΠPSI。协议首先使用GBF 存储各参与方的集合，利用秘密共享的性质达到数据安全的目的，使数据的传输更安全、高效；然后，利用OT 与份额置换保护了各参与方的数据隐私，避免了参与方在交互过程中可能泄露集合元素信息的问题；最后，云服务器计算出集合交集的GBF，并将它发送给各参与方，保证各参与方运行该协议可以公平地得到结果。

1 预备知识

1.1 混淆布隆过滤器

图1 向GBF中插入元素Fig.1 Inserting elements into GBF

1.2 安全模型

半诚实参与方完全按照协议指令执行，但在协议执行过程中会记录下收集到的一切信息，并试图利用这些中间信息推测出额外的隐私信息。敌手会腐败部分参与方，并根据参与方的信息试图推导出更多隐私信息，但是不能篡改信息。

PSI 计算协议的安全性定义需满足协议的参与者除最后的计算结果外无法得知其他参与者的任何信息。在随机预言机模型下使用选择明文攻击下的不可区分性（INDistinguishability under Chosen-Plaintext Attack，IND-CPA）游戏来证明协议的安全性［17］。游戏过程如下：

1）初始化。确定挑战者实体集合U以及两个相同长度的消息M0和M1。

2）接收安全参数λ，挑战者运行密钥生成算法生成公私钥对公开公钥，保存私钥。

3）查询。概率多项式算法时间（Probabilistic Polynomial-Time，PPT）敌手A 通过预言机询问与U进行交互，预言机询问对敌手A 在实际攻击中的能力进行了模拟。协议中所涉及到的预言机询问如下：

①Execute(U)：该询问对敌手A 的窃听能力进行了模拟（此时A 可以获取信道中传送的消息），将协议实际执行过程中实体间传送的所有消息发送给A。

③Corrupt(U，Pi)：返回的私钥和隐私输入数据。该询问模拟了敌手的腐败能力（此时A 可以腐败部分参与方来获取信息）。

④Collude(S)：该询问模拟了敌手的合谋能力（此时A 可以腐败云服务器从而获取服务器上存储的所有信息），返回云服务器上存储的所有信息。

⑤Collude(V)：该询问同样模拟了敌手的合谋能力（此时A 可以腐败部分参与方和云服务器来获取他们掌握的所有信息），V⊂U，返回集合V中所有参与者拥有的信息以及云服务器上存储的所有信息。

4）挑战。敌手A将消息M0，M1发送给挑战者，挑战者随机选取，加密Mb并返回密文c。

5）测试。敌手A 根据上述预言机询问中得到的信息输出对于b的猜测b′，若b=b′，则A 赢得游戏（记为事件Succ）。

敌手A 赢得IND-CPA 游戏的优势定义为：

定义1 若对于任意的PPT 敌手A，存在一个函数ε使AdvA(λ) ≤ε，则称协议是IND-CPA 安全的，其中函数ε可忽略。

2 多方隐私集合交集协议ΠPSI

为了给患者提供更加精准的医疗服务，医院希望通过云服务商来实现不同医院相同患者的信息共享，但是又不希望泄露各自拥有的其他患者病例信息。该问题可以转化为基于云服务器的多方PSI 问题。本章结合GBF 与OT 技术提出基于云服务器的多方PSI 系统模型，并对具体设计思路和协议进行详细描述，使用的参数及含义如表1 所示。

表1 参数及其含义说明Tab.1 Description of parameters and their meanings

2.1 系统模型

假设参与计算的不同医院分别为参与方P1，P2，…，Pd，每个参与方Pi(1 ≤i≤d) 持有的患者信息为集合Xi=。希望在不泄露除交集以外的任何隐私信息的情况下，通过云服务器S计算出各自集合的交集X1∩X2∩…∩Xd，同时各参与方希望能同时得到交集的结果，具体的系统模型如图2 所示。

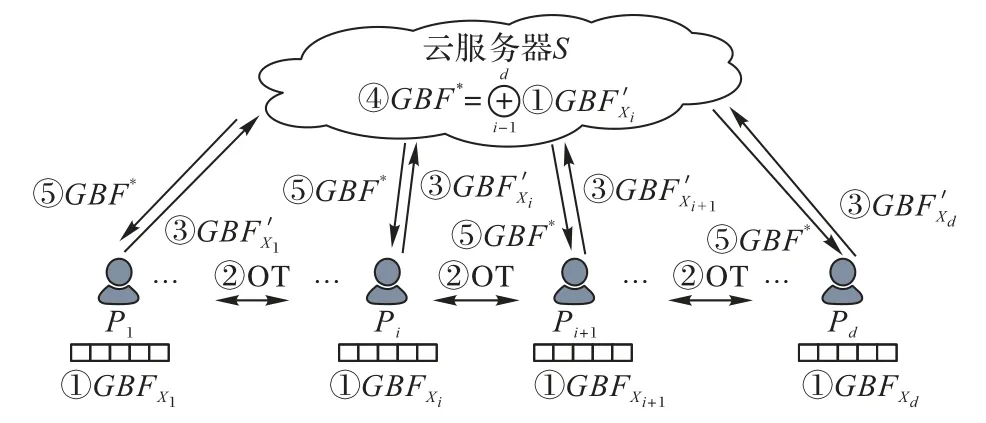
图2 系统模型Fig.2 System model

2.2 设计思路

协议ΠPSI能够实现多方安全交集计算，在思想上等同于直接求出集合交集的GBF，查询此交集的GBF 存储的是否是元素的所有子份额。同时为了实现公平性，云服务器S将交集的GBF 发送给参与方Pi，参与方Pi通过查询GBF，进而确定元素是否属于交集。

首先，参与方Pi(1 ≤i≤d)协商使用映射范围为[1，m]的哈希函数：H={h1，h2，…，hk}，参照1.2 节将集合元素的k份子份额依次存储到混淆布隆过滤器的对应位置

根据哈希函数的无碰撞性可知，对于∀xiq∈Xi，∀xcq∈Xc(c=(i+1)%d)，若xiq=xcq，则hj(xiq)=即通过哈希映射，参与方在互不知道对方元素的情况下，总可以将相同元素存储在具有相同索引值的GBF 中。对于给定集合Xi(1≤i≤d)及其交集X1∩X2∩…∩Xd，设GBF2是通过ΠPSI协议求得，GBF1是直接采用交集生成，如果GBF1[id]存储的为交集中元素的子份额，则有GBF2[id]=0，id∈[1，m]。根据GBF 的创建规则可以得知GBF1[id]和GBF2[id]中存储的结果只包含集合中的元素信息和随机生成的λ字符串，因为GBF1[id]和GBF2[id]使用的是相同的哈希函数H，所以∀id∈[1，m]，GBF2[id]存储的是交集中元素的子份额当且仅当GBF1[id]存储的是同一元素的子份额。同理，GBF2[id]存储的是随机生成的λ字符串当且仅当GBF1[id]存储的随机生成的λ字符串。子份额的分布仅仅取决于元素以及哈希函数，随机字符串是均匀分布的，GBF2[id]和GBF1[id]的分布是相同的。因此，云服务器S对收到的储存相同元素子份额的GBF 逐位异或运算必定得到

2.3 协议ΠPSI描述

多方隐私集合交集协议ΠPSI的具体描述如下：

步骤一 协商与初始化。参与方Pi(1 ≤i≤d)分别持有拥有ni个元素的集合Xi，Pi协商确定GBF 中的哈希函数：H={h1，h2，…，hk}，映射范围为[1，m]。Pi创建GBF 并初始化为空，将集合Xi中的元素xiq拆分为k个λ位子份额，对xiq进行k次哈希得到k个索引值hj(xiq)(1 ≤j≤k)，将子份额存储到，进而有中。在插入完集合Xi中所有元素之后，遍历，如果为空，则

步骤五 查询交集中的元素。云服务器S将GBF*发送给参与方Pi。参与方Pi查询q≤ωi)确定xiq的所有子份额是否在交集之中，进而确定xiq是否为交集中的元素。

3 正确性分析

4 安全性证明

定理1 令G是一个阶为大素数p的循环群，A 是在多项式时间tA内攻击IND-CPA 安全性的PPT 敌手。设A 可发送少于qexe次的Execute 询问和qsen次的Send 询问，最多qh次的随机预言机询问，因此有：

证明 敌手A 攻击协议ΠPSI的IND-CPA 安全性，构建一个敌手B 通过A 来攻击DDH 问题。如果A 能够以不可忽略的优势ε攻破IND-CPA 安全性，B 可以不可忽略的优势攻破DDH 问题。过程如下：

1）初始化。确定挑战用户实体集合U以及两个相同长度的消息M0和M1发送给B。用户实体集合U包括协议ΠPSI中的d个参与者以及一个服务器S。B 根据安全参数λ生成公私钥对(pk1，sk1)，(pk2，sk2)，保留私钥sk1，sk2，则B 的挑战四元组为

2）询问。协议ΠPSI中涉及到的预言机询问如下：

①H(M)：若列表L已存在记录(M，r)，则返回r；否则随机选取r∈G，将记录(M，r)存储进列表L，返回r。

②Send(Pi，Pc)：参与方Pi(1 ≤i≤d) 和参与方Pc(c=(i+1)%d)之间运行k-out-of-mOT 协议，返回执行过OT 协议的

③Send(Pi)：参与方Pi进行份额置换操作，返回

④Send(Pi，S)：云服务器S对收到的进行逐位异或运算得到交集的GBF*，返回GBF*。

⑤Execute(Pi，S)：基于Send 询问成功的情况，返回

⑥Corrupt(Pi)：返回参与方Pi的数据集Xi。

进一步通过一系列的混合游戏Gamen(n∈[0，4])来证明定理1，从游戏中敌手的真实攻击开始，到游戏中敌手的没有任何优势时结束。

①Game0：在随机预言机模型中，Game0与真实的攻击相对应，由定义1 可得：

②Game1：除了通过列表L中的记录来模拟预言机中哈希函数，其余部分与Game0相同，仍与真实的攻击相对应。因此Game1与现实中敌手攻击是不可区分的，故有

③Game2：除了中止H(x)和H(y)哈希碰撞，其余部分同Game1一样。根据生日悖论可知，发送qexe次的Execute 询问、qsen次的Send 询问和qh次的随机预言机询问时，发生哈希碰撞的概率最多为pr2，故

⑤Game4：通过DDH 来模拟协议ΠPSI的执行。给定DDH样 例 (A=gx，B=gy)，随机选择α，β∈Ζp，令E(x)=Aα，E(y)=Bβ，存在四元组DDH(g，A，B，DDH(E(x)，E(y)))。事件Exp4发生当敌手A对预言机的哈希H′进行了E(x)=Aα，E(y)=Bβ询问，且存在：

5 性能实验与结果分析

本章对ΠPSI协议的计算复杂度与通信复杂度以及协议的运行时间进行了分析，与相关的PSI 协议的性能对比结果如表2 所示。

表2 不同方案的PSI性能分析Tab.2 PSI performance analysis of different schemes

ΠPSI协议中d个参与方两两之间运行k-out-of-mOT 协议和份额置换时共需要dλm个字符操作。d个参与方向云服务器S发送GBF 时需要dλm个字符操作。因此，协议的计算复杂度为O(dλm)，通信复杂度为O(dλm)。可以看出，ΠPSI协议的计算复杂度和通信复杂度都与参与方集合所包含的元素总个数ω无关。这是由于ΠPSI协议将集合中的元素存储进大小为m的GBF 之中，之后所有的操作都是基于GBF 来对数据进行处理的。因此，与文献方案相比，ΠPSI协议具有较优的计算性能。此外，ΠPSI协议还具有公平性，即所有参与方同时获取PSI 的计算结果。

为了更直观地对比本文协议与MPSI［9］、PSImple［10］和PISum［12］的时间开销，本文进行了仿真实验和结果分析。需要指出的是，协议所耗费的时间指10 次实验中的平均耗时。实验配置：搭载Intel Core i5-5200U CPU @ 2.20 GHz，机带RAM 4.00 GB，x64 处理器的笔记本电脑。

考虑集合包含元素总个数的变化对协议存储时间的影响。假设参与方数量d=20；哈希函数个数k=128；安全参数λ=128；混淆布隆过滤器大小m=105。分别选取集合包含的元素个数ω=28，29，210，211，212进行对比实验，总集合大小和协议存储时间的关系如图3 所示。

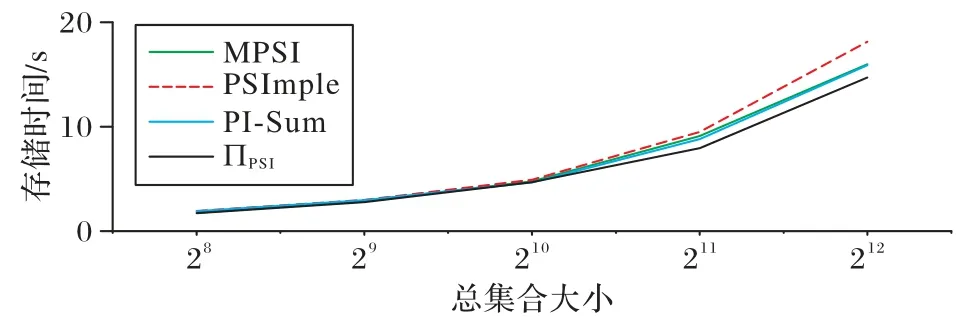
图3 总集合大小与存储时间的关系Fig.3 Relationship between total set size and storage time

根据图3 可以看出，随着总集合大小的增加，所有方案的存储时间基本呈线性增加，但当固定总集合大小时，本文的ΠPSI协议具有最低的存储时间。

考虑集合包含元素总个数的变化对协议通信开销的影响。假设参与方数量d=20；哈希函数个数k=128；安全参数λ=128；混淆布隆过滤器大小m=105。分别选取集合包含的元素个数ω=28，29，210，211，212进行对比实验，总集合大小和协议通信开销的关系如图4 所示。

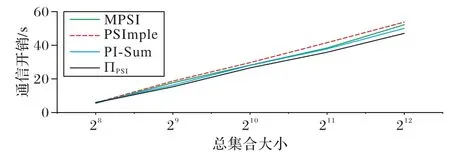
图4 总集合大小与通信开销的关系Fig.4 Relationship between total set size and communication overhead

根据图4 可以看出，随着总集合大小的增加，所有方案的存储时间基本呈线性增加，但当固定总集合大小时，本文的ΠPSI协议具有最低的通信开销。

考虑集合包含的元素总个数变化对运行时间之间的影响。假设参与方数量d=20；哈希函数个数k=128；安全参数λ=128；混淆布隆过滤器大小m=105。分别选取集合包含的元素个数ω=28，29，210，211，212进行对比实验，协议运行时间与集合包含元素个数的关系如图5 所示。

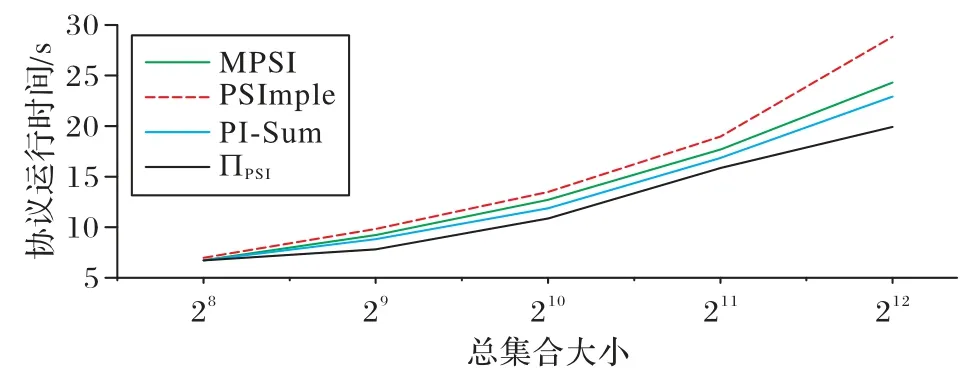
图5 总集合大小与协议运行时间的关系Fig.5 Relationship between total set size and running time

根据图5 可以看出，随着总集合大小的增加，所有方案的运行时间基本呈线性增加。但ΠPSI协议的运行时间增长速率最慢。且当固定总集合大小时，本文的ΠPSI协议具有最低的运行时间。

此外，ΠPSI协议中参与方个数的变化对协议的运行时间也会产生一定的影响。假设集合包含的元素总个数ω=103，保持其余参数不变。分别选取参与方个数d=101，102，103，104，105进行对比实验，协议运行时间与参与方个数的关系如图6 所示。

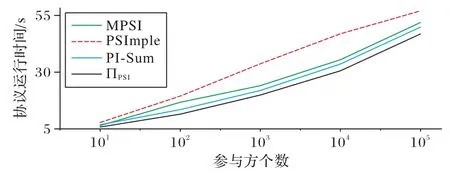
图6 参与方个数与协议运行时间的关系Fig.6 Relationship between number of parties and running time

由图6 可以看出，所有协议的运行时间都随参与方个数的增多而逐渐增加。但当参与方个数固定时，协议ΠPSI的时间开销均低于其他方案。

综上，ΠPSI协议在一定程度上节约了多方PSI 的存储开销、通信开销和计算的时间开销，提高了计算效率，此外根据协议ΠPSI的执行过程可知，参与方Pi(1 ≤i≤d)在协议的步骤五中可以同时得到交集所对应的混淆布隆过滤器GBF*，通过本地查询可以得到交集的结果，实现了公平多方PSI 计算。因此，协议ΠPSI的整体效率优于所对比的文献。

6 结语

隐私集合交集计算是安全多方计算的特定问题，常被用于智慧医疗、商业广告等领域，但现有多方PSI 协议中参与方存在不公平性问题，因此提出了一个基于云服务器外包的公平多方PSI 协议。利用GBF 和OT 的结合，将交集的计算转换为GBF 的逐位异或运算。协议执行结束后，参与方均能得到交集结果，实现了公平性。理论分析和实验结果表明本文所提出的协议在实现公平性的同时又有着较低的存储、通信和计算时间开销。随着区块链技术的不断发展，存在着数据的安全共享与数据的高速流通问题，因此，下一步要研究将区块链技术与云服务器结合构建公平多方PSI 协议。