配电网电缆接头SiR-XLPE绝缘界面热应力与击穿电压关系的实验与分析
2023-09-26郭耀栋赵一枫陆代强
郭耀栋,赵一枫,胡 冉,陆代强,刘 刚
(华南理工大学电力学院,广州 510640)
0 引言
配电网电缆接头是电缆线路的薄弱环节,对其故障进行研究是保证线路安全运行的关键。尤其是在重载线路中,电缆接头更易发生过热、放电击穿现象,最终可能会引发火灾、爆炸等电力事故[1-4]。
配电网电缆接头在安装施工过程中易造成硅橡胶(SiR)-交联聚乙烯(XLPE)交界面(以下简称绝缘界面)处形成缺陷(引入杂质、受潮、气隙和破损等),导致电场集中等问题[5-7]。据统计表明,电缆接头故障约占线路总故障的70%,大部分的电缆接头故障始于绝缘界面的树枝放电[8],而绝缘界面的应力对绝缘材料的树枝放电和击穿电压都有重要影响[9]。
绝缘界面的应力由电应力、热应力和机械应力叠加而成。由于电缆接头内部应力锥制作技术日益成熟,绝缘界面的电场得到极大改善,故可忽略电缆接头运行过程中产生的电应力[10]。机械应力是由接头预制件初始设置的定伸强度和过盈率决定的[11-12],故在接头运行过程中,绝缘界面的应力变化主要由接头温度升高导致的热应力决定。关于绝缘界面温度和热应力的研究,文献[13-18]通过有限元仿真计算电磁-热-应力多场耦合下绝缘界面温度场和热应力以及界面开裂规律。针对绝缘界面击穿的研究,文献[19]对不同老化程度的绝缘界面进行击穿实验,探究老化后材料属性变化对局部放电的影响情况;文献[20]通过界面压力可调的电痕破坏实验,得到界面压力越大、绝缘界面放电面积越小、界面碳化深度越大的结论。由此可见,已有大量学者单独针对接头内温度分布和绝缘界面击穿进行研究,但接头故障往往是接头热效应与绝缘界面击穿共同作用导致的。配电网输电线路负荷状态不仅从热效应角度对电缆接头故障造成影响,还通过热应力间接影响绝缘界面的击穿,进而对绝缘材料进行短时间劣化,使绝缘失效造成故障。因此,需要开展电磁-热-应力的配电网电缆接头SiR-XLPE绝缘界面击穿研究。
针对实际接头故障问题,本文确定的研究思路如下:通过构建电磁-热-应力多场耦合的电缆接头仿真模型,建立配电网电缆不同稳态负荷状态下绝缘界面温度分布及其与绝缘界面压力的联系;开展电缆接头绝缘界面电压击穿实验,探究界面压力对绝缘界面电压击穿特性的影响;结合仿真与实验的结果,为实际线路运维过程中降低电缆接头故障提供不同的负荷调控策略。
1 接头结构与物理场控制方程
1.1 配电网电缆中间接头结构
配电网电缆中间接头在线路中起到接续和交叉互联接地的作用,是线路中的重要环节。电缆中间接头结构见图1,组成部分主要包括应力锥、高压屏蔽管、硅橡胶和主绝缘。以某厂家生产的10 kV冷缩式电缆中间接头为样本,建立电缆中间接头有限元仿真模型,其结构参数如表1所示。
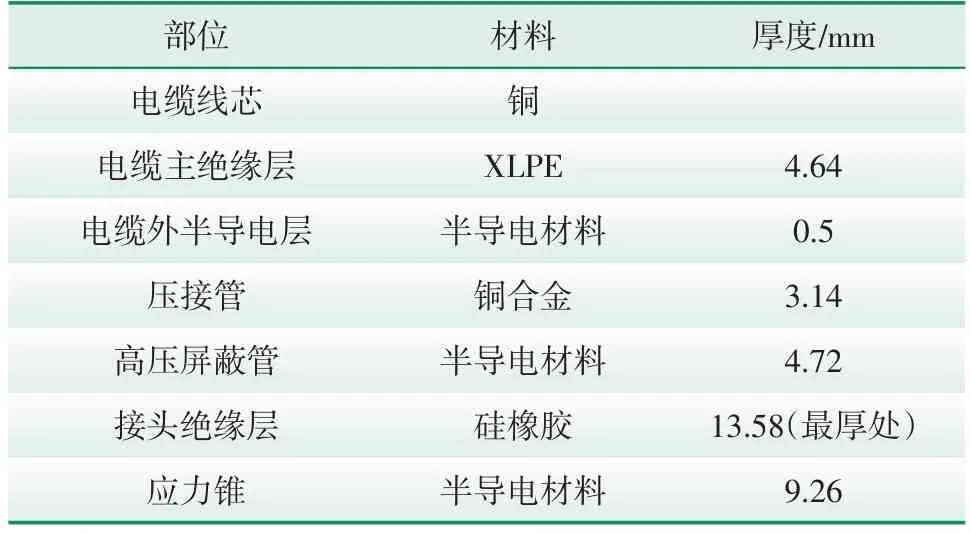
表1 10 kV冷缩式电缆中间接头结构参数Tab.1 Structural parameters of intermediate joints for 10 kV cold shrink cables

图1 配电网电缆中间接头轴向剖面图Fig.1 Axial profile of cable intermediate joint in distribution network
1.2 各物理场的控制方程
本文采用电磁热源,并设置导体电导率为温度的函数,建立导体电导率的温度依赖性。铜导体的电导率σ与导体工作温度Te的函数为:
式中:Tref为导体初始参考温度,K;ρref为导体在初始温度下的参考电阻率,Ω·m;αCu为铜导体电阻率温度系数。
电磁场控制方程为:
式中:∇为算子;H为磁场强度;J为电流密度矢量;Je为外部电流注入密度矢量;B 为磁感应强度;A 为矢量磁势;E为电场强度矢量;v为电势值;t为时间。
温度场控制方程为:
式中:ρ为材料密度;Cp为常压热容;Tw为温度场节点温度;u为位移;k为导热系数;Q为热源。
应力场控制方程为:
式中:s表示应力张量的大小;so为应力张量初始值;Fv为体积力;ε为应变张量的大小;ε0为应变张量初始值;εth为热膨胀导致的应变张量大小;Es为杨氏模量;vs为泊松比;αs为热膨胀系数;Ts为应变温度。
2 接头绝缘界面热应力的仿真计算
2.1 有限元仿真模型构建
2.1.1 建模假设
电缆接头的电-热耦合作用直接影响电缆的产热和散热,进而影响电缆绝缘界面热应力,因此构建的模型中需要同时考虑电磁场、温度场和应力场。为了减少模型计算量,建模时进行了简化[10]:
(1)电缆本体和接头主体主要组成部分为轴对称结构,且接头接地柱等少量非对称结构对电缆导体温度影响很小,模型简化为二维轴对称。
(2)相对于导体损耗,绝缘层的介质损耗可忽略不计;实验回路中铝护套单端接地,忽略护套损耗。
(3)电缆的工频电磁场按稳态场处理,控制方程中不含时间项,忽略位移电流的影响,忽略铁磁材料的磁滞效应并设为各向同性的媒质,导体的电导率σ是随温度变化的量。
2.1.2 参数设置与网格剖分
本文运用COMSOL Multiphysics 有限元仿真软件对配网中间接头进行了建模,其主要结构的材料参数如表2所示。
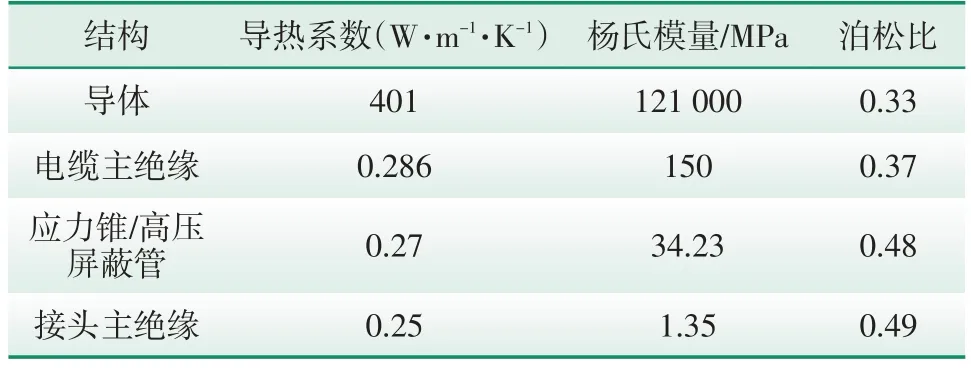
表2 电缆接头主要结构材料参数Tab.2 Main structural material parameters of cable joints
以正三角形为参考基准,使用COMSOL Multiphysics中的网格自动划分功能,通过物理场控制网格,对电缆中间接头模型进行有限元网格剖分。以网格划分中极细化划分为标准,对比不同网格划分下的仿真计算误差。其中,超细化网格划分计算误差为0.22%,较细化网格划分计算误差为0.56%,细化网格划分计算误差为1.12%。为了提高计算精度与减少计算量,网格单元大小设置为较细化。电缆中间接头有限元网格划分三维示意图如图2所示。

图2 网格剖分示意图Fig.2 Schematic diagram of mesh refine
2.1.3 边界条件
为提高电缆温度场分布的计算效率,需要将电缆的开域场转变为闭域场,即设置边界条件进行约束。电缆传热问题的边界条件可归结为三类:第一类为已知边界温度;第二类为已知边界法向热流密度;第三类为对流边界条件,即已知表面对流换热系数和环境温度。三类边界条件的控制方程分别如式(12)—(14):
式中:Γ1、Γ2、Γ3分别为三类边界条件的积分边界;λ为土壤的导热系数,W/(m·K);q为热流密度,W/m2;T为边界温度;x、y为二维模型中的x方向和y方向;n为边界对应的法向方向;Tf为第三类边界对应的流体温度;αh为表层土壤与空气的对流换热系数。
本文研究的电缆接头直接暴露在空气中,属于第三类边界。电缆接头多敷设于电缆沟或隧道内,其周围空气流速小于0.15 m/s,属于自然对流,其自然对流换热系数为7.5 W/(m·K),环境温度为20 ℃,接头两端设为绝热与磁绝缘,电缆接头绝缘界面的初始面压为0.25 MPa[18],接头表面设置为自由,即没有任何位移和外力。
2.2 电磁-热-应力耦合仿真实验结果
根据上述建模与参数设置对电缆接头进行热应力仿真计算,当电缆负荷为稳态载流量时,即导体温度达到90 ℃时,1/4 电缆接头二维温度场分布如图3 所示,绝缘界面温度畸变导致界面热应力变化,以仿真模型左边应力锥为零点,电缆接头的高压屏蔽管方向为x 轴的正半轴,绘制绝缘界面热应力变化分布(如图4 所示),界面应力分布呈“澡盆”形状,根据实际接头故障解剖分析可知,引发接头绝缘界面击穿故障多发生于应力锥与高压屏蔽管之间的绝缘界面段,即“澡盆”的底部[3-18]。故本文研究的界面热应力为图3与图4所示的界面击穿频发处热应力。分析图4 可知,当导体温度为90 ℃时,绝缘界面应力变化基本为0.30 MPa,即绝缘界面总应力值为0.55 MPa。

图3 中间接头二维温度场分布Fig.3 Temperature field distribution of intermediate joint

图4 绝缘界面应力变化分布Fig.4 Distribution of stress variation at insulated interface
通过改变仿真模型的导体负荷电流,使导体温度从90 ℃递降,分别记录不同温度场对应的绝缘界面热应力变化值,各电缆导体稳态温度下对应的绝缘界面总热应力值如表3所示。

表3 不同导体温度下绝缘界面的热应力Tab.3 Thermal stress of insulated interface at different conductor temperatures
由仿真结果可知,当电缆接头达到某一稳态负荷运行时,由应力锥至高压屏蔽管之间的绝缘界面应力分布呈“澡盆”曲线,靠近应力锥与高压屏蔽管附近的界面应力较大,其余大部分部位应力较小且基本一致,本文研究绝缘界面大部分部位的界面应力对绝缘界面起始击穿电压的影响。根据表3 可知,绝缘界面应力随电缆导体负荷电流的增大而增大,当电缆导体负荷电流为548 A,即电缆导体温度维持额定稳态工作温度90 ℃时,绝缘界面最高热应力可达0.55 MPa,为初始面压的2 倍以上。温度和热应力将加速绝缘界面材料的热老化与开裂,同时影响绝缘界面的电压击穿特性,造成绝缘材料电热联合老化[19]。
3 SiR-XLPE绝缘界面电压击穿实验
3.1 绝缘界面电压击穿实验
在上述绝缘界面热应力研究的基础上,开展绝缘界面电压击穿实验,探究绝缘界面处的应力-电压击穿特性。以电缆内部形态结构为基础,设计可改变界面压强的绝缘界面电压击穿试样,并搭建电压击穿实验平台。
3.1.1 试样准备
试样模型如图5 所示,模拟实际电缆接头应力锥与高压屏蔽管间绝缘界面的结构,既体现了多层复合介质界面的结构,又便于加压实验。模型中由上到下的结构分别为:有机玻璃上盖板、小块有机玻璃压板、硅橡胶切片、金属电极、XLPE绝缘切片、有机玻璃下盖板。为了模拟电缆接头绝缘界面中缺陷处畸变的电场场强[10-19],将两个电极头部设计为半圆形尖端,尖端间距2 cm,两个电极夹在硅橡胶与XLPE绝缘切片之间,制成绝缘界面试样,通过改变6个弹簧的形变量改变界面间压力[20-23]。同时,本实验为了使两个电极间的绝缘界面所受压力均匀,在两电极之间对应的硅橡胶上方增加小块刚性有机玻璃压板,且小块刚性有机玻璃压板处于整个试样的几何中心,使6 个弹簧对有机玻璃的压力全部通过小块有机玻璃压板均匀施加至极间绝缘界面。有机玻璃下盖板的面积为200 mm×120 mm,小块有机玻璃盖板的面积为48 mm×48 mm,硅橡胶与XLPE绝缘切片均为1 mm厚。
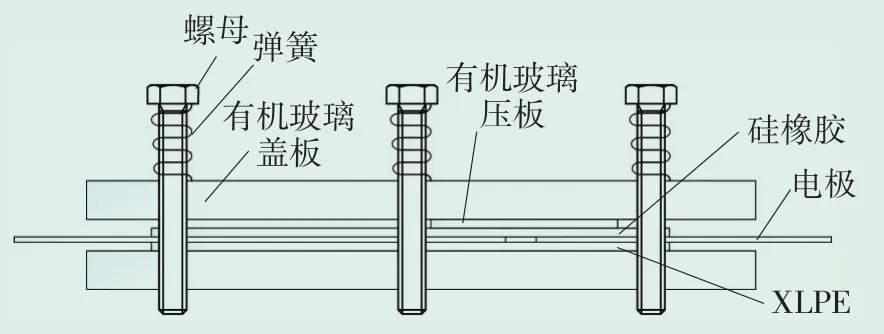
图5 试样模型图Fig.5 Sample model diagram
为了研究绝缘界面在不同压力下的电压击穿特性,本文借用钢制弹簧的形变量和弹簧系数来表征绝缘界面处所受的压力大小,弹簧系数可由式(15)计算,改变弹簧的形变量,运用式(16)胡克定律即可计算不同弹簧形变量下的压力大小,再通过测量试样的受力面积,通过式(17)即可求得绝缘界面的界面压强大小。
式中:K为弹簧系数;G为弹簧线材的弹性模量;d为弹簧线径;D 为弹簧中径;Nc为弹簧有效圈数;F 为弹簧弹力;X为弹簧形变量;S为作用面积;P为作用压强。
本文所用的弹簧参数如表4所示。

表4 弹簧参数Tab.4 Spring parameters
结合不同线路负荷下的界面热应力仿真计算结果,根据式(15)—(17)可计算出不同负荷状态下的试样弹簧形变量,如表5所示,其中界面的初始压力为0.25 MPa。
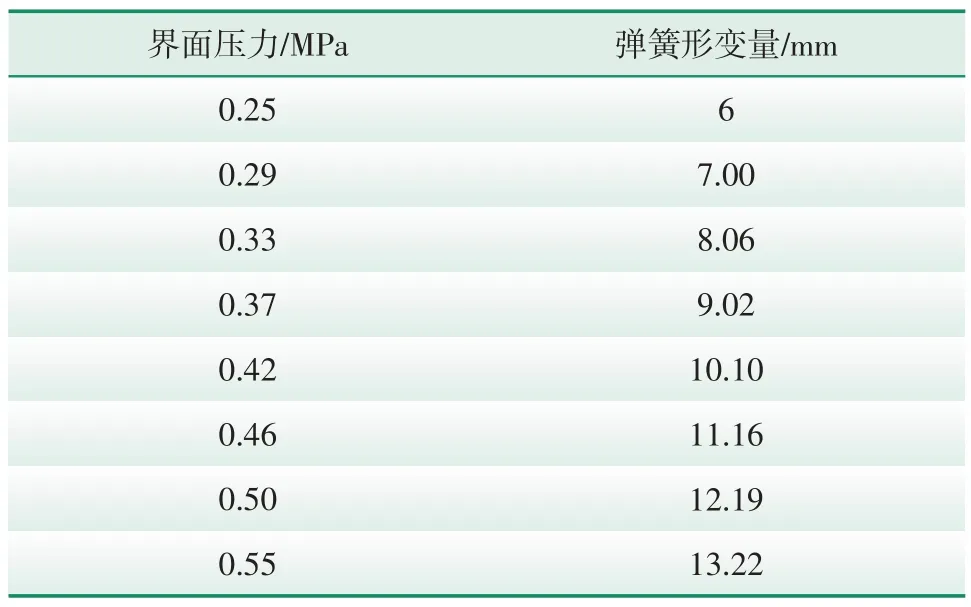
表5 不同界面压力下的试样弹簧形变量Tab.5 Spring deformation quantity of the sample under different interface pressure
3.1.2 实验平台搭建
根据上述理论分析与试样的制备,搭建绝缘界面受压下的电压击穿实验平台,对两个电极施加电压,记录不同压强下的绝缘界面起始击穿电压,研究绝缘界面电压击穿特性。实验的主要设备包括高压变压器(HVT)、保护阻抗、电容器、采样电阻和示波器等。实验电路与搭建实验平台如图6 所示。示波器采样频率设置为1 GS/s(采样时间1ns)。

图6 实验电路及实验平台示意图Fig.6 Schematic diagram of experimental circuit and experimental platform
搭建整个绝缘界面电压击穿电路,在接电之前检查各处接地情况与线路连接情况后调压器接电,调节操作盘匀速升压,当听到试样发出强烈的电晕声时减缓升压速度,此时试样的绝缘界面产生间歇性击穿,当界面电极间出现持续明亮白光放电通道时,即发生绝缘界面击穿。至绝缘界面击穿后,迅速将操作盘回旋至零值并按下停止按钮,对现场进行放电操作,通过示波器记录起始击穿电压。
3.2 绝缘界面电压击穿实验结果
根据仿真中所得不同导体温度对应的热应力,计算不同热应力所需弹簧形变量,通过改变弹簧形变量即可设计不同界面压强下的绝缘界面电压击穿实验,不同负荷状态下的每个弹簧形变量见表5。本文根据不同负荷状态设计了8 个不同界面压强下的绝缘界面电压击穿实验,每个界面压强进行3组电压击穿实验,并记录绝缘界面起始击穿电压,根据3 组实验的绝缘界面起始击穿电压平均值,确定该界面压力下的绝缘界面起始击穿电压。
当界面压力为0.25 MPa 时,根据示波器触发信号获得3组绝缘界面起始击穿电压波形及其起始击穿电压值(如图7所示)。本实验选择记录起始击穿电压而非完全击穿时电压,可以有效避免击穿过程中碳化界面绝缘材料的随机性导致电场畸变的随机性,影响整个绝缘完全击穿的进度,进而影响绝缘完全击穿时的极间电压。

图7 0.25 MPa界面压力下起始击穿电压波形Fig.7 Initial breakdown voltage waveform at 0.25 MPa interface pressure
根据图7 中3 组0.25 MPa 界面压力的绝缘界面电压击穿实验数据处理结果可知,当界面压力为0.25 MPa 时,绝缘界面起始击穿电压的平均值为20.20 kV。同理对表5 中其他界面压力下的绝缘界面电压击穿实验数据进行处理,得到不同界面压力下的绝缘界面起始击穿电压(如表6所示)。
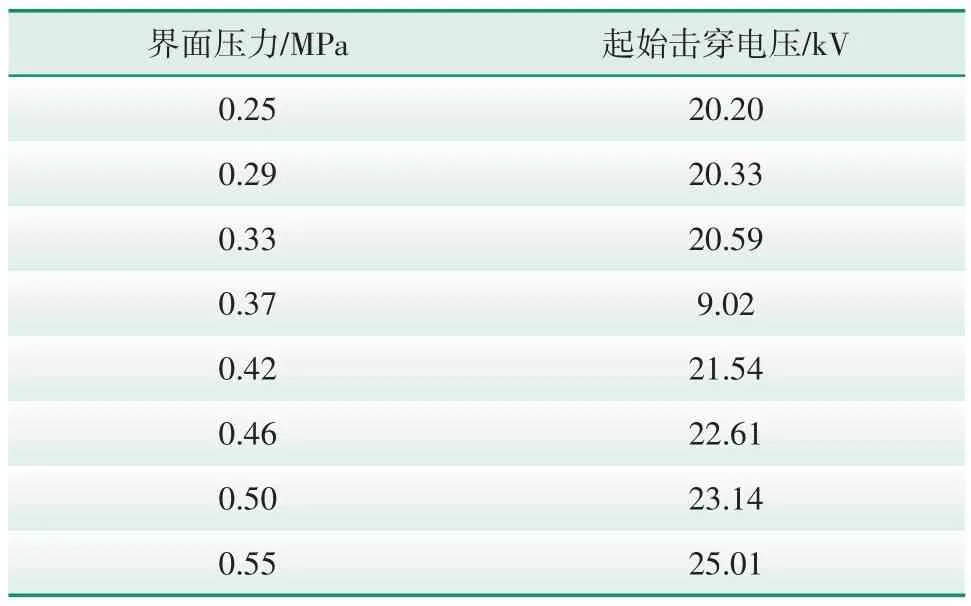
表6 不同界面压力下绝缘界面起始击穿电压Tab.6 Initial discharge breakdown voltage of insulation interface under different interface pressures
将不同界面压力与起始击穿电压的关系进行二次多项式拟合,得到如图8所示的拟合曲线。
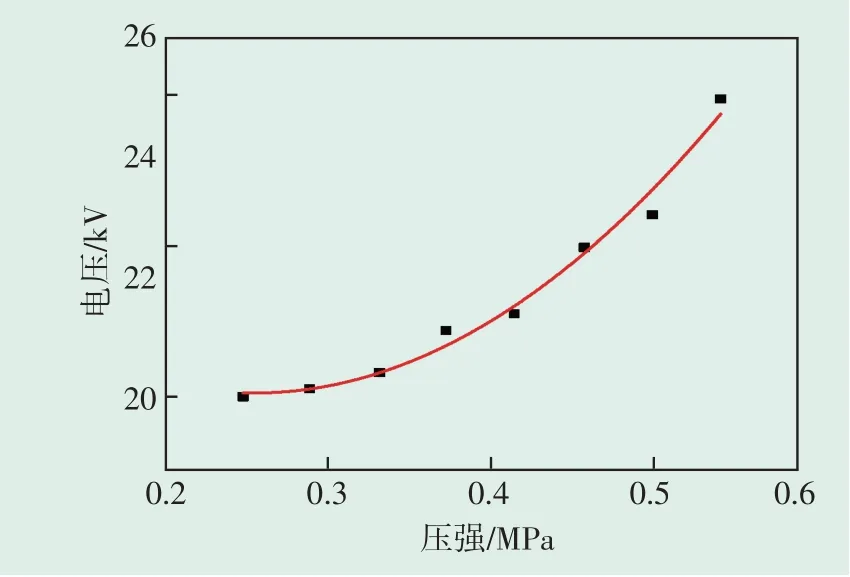
图8 不同界面压强下的起始击穿电压二次多项式拟合曲线Fig.8 Quadratic polynomial fitting curve of initial breakdown voltage at different interface pressures
根据图8 中的拟合曲线可知,绝缘界面起始击穿电压随着界面压强的增大逐渐增大,且随着界面压强的增大,绝缘界面起始击穿电压的增长速率逐渐增大,起始击穿电压在低界面压力下趋向平缓不变。在初始界面压强0.25 MPa下,绝缘界面的起始击穿电压为20.20 kV,当绝缘界面压强为0.55 MPa时,绝缘界面的起始击穿电压为25.01 kV,相比于初始面压下起始击穿电压增加了24.75%左右。
绝缘界面试样在制备过程中,会因为人为因素导致界面不平整,当界面压强较低时,这种不平整性更加突出,在不平整处会存在一定的微小空腔,空腔中空气的介电常数远低于绝缘界面的介电常数,当两端电极加以高压时,会在空腔处产生电场畸变,并产生局部放电,加速绝缘击穿。当界面压强较大时,绝缘界面相互挤压使得微小空腔数量变少,界面相对较为平整,电场较为均匀,界面不易产生电压击穿,故起始击穿电压变高[22]。因此,运行电缆导体稳态温度越高,导致电缆内部界面压强越大,缺陷处界面空腔缩小不易形成放电,界面起始击穿电压越高,绝缘性能越好。
3.3 结果分析
从上述分析可知,绝缘界面起始击穿电压随着界面压强的增大逐渐增大。然而,在界面压强高于0.40 MPa 后,随界面压强的升高绝缘界面的起始击穿电压上升尤其明显,界面压强处于0.25~0.40 MPa时,绝缘界面起始击穿电压变化不明显。结合该接头稳定负荷条件下仿真结果分析可发现,当电缆接头线路负荷电流较低时,绝缘界面压强也相对较低,故接头内部绝缘界面的起始击穿电压较低,绝缘界面击穿较易发生。因此,配电网线路中负荷状态不仅对电缆接头绝缘的热老化过程造成影响,而且对其绝缘界面击穿的形成起到重要作用。
配电网电缆接头在运行过程中,电缆接头的温度会不断对绝缘材料进行热老化,这个过程是缓慢且漫长的,温度越高热老化速度越快。从微观角度来看,温度升高加快了电子撞击绝缘材料大分子链的速率,促使分子链断裂,加快了热氧反应,使得绝缘材料加速劣化。另一方面,绝缘界面击穿会在短时间内释放大量热量和大量电子,这些带有高能量的电子在高电场的加速下会迅速撞击并破坏绝缘材料的分子链,使得绝缘材料在短时间内劣化,且释放的高热量使绝缘有机大分子材料迅速氧化成炭黑。由于配电网继电保护设置相对宽松,长时间的大电流整定使得绝缘界面反复发生界面击穿,而绝缘界面完全击穿前的界面击穿对绝缘材料的劣化是迅速且严重的,故引发电缆接头的重大事故。
在实际线路运维过程中,对于不同电缆接头状态配网线路可针对性地采用不同的运维策略。对于已知带缺电缆接头运行的配网线路,可适当提高电缆负荷,促使绝缘界面热应力增大,提高绝缘界面起始击穿电压,不仅达到增容作用,还可降低发生绝缘界面击穿的概率,提高线路运行的可靠性。
4 结束语
本文通过分析配电网电缆接头在不同负荷状态时内部绝缘界面的电压击穿特性,建立了电缆接头电磁-热-应力多场耦合的界面热应力的仿真计算模型,进行了对应的绝缘界面电压击穿实验,主要得出以下结论:在实际线路运维过程中,可以适当提高电缆负荷,促使绝缘界面热应力增大,提高绝缘界面起始击穿电压。但提高负荷产生的热效应也会导致线路过热引发事故,故实际线路负荷的调控要根据线路的运行状况而定,寻找降低电缆导体热效应与抑制绝缘界面击穿的负荷状态最佳点。
