基于小波算法的小电流接地系统高阻接地故障的识别
2023-09-26张紫凡梁展弘邝国员刘彬博
黄 雯,张紫凡,梁展弘,邝国员,王 玕,刘彬博
(1.广西电网有限责任公司南宁供电局,南宁 530031;2.广州城市理工学院,广州 510800)
0 引言
小电流接地方式在低压配电网系统中可短时间带故障运行[1],供电可靠性较高,在我国低压配电系统中应用广泛。由于小电流接地系统的故障电流小,其本身故障选线的准确性不高[2]。当配电网的架空线或地下电缆因为各种原因导致线路直接或间接与碎石、树枝、建筑物发生连接的,故障线路会发生高阻抗故障,与普通单相接地故障相比,高阻接地故障的暂态电阻较大,整体电流变化小[3],一般的继电保护装置难以识别甚至无法识别。而且高阻接地故障经常伴随着电弧的产生,发生电弧燃烧的概率较高,如果不及时处理,故障范围则可能进一步扩大。
传统的故障诊断方法主要基于数字信号处理算法,这类算法存在运算量大、鲁棒性不强等问题。在高阻接地故障识别领域,小波变换算法已经被广泛应用[4]。小波变换具有信号分析处理和特征提取能力,可以对高阻接地故障特征进行有效提取和准确诊断。与传统方法相比,基于小波变换的高阻接地故障识别方法具有计算复杂度低、鲁棒性强、准确性高等优点[5],在高阻接地故障燃弧检测领域表现突出。
目前小电流系统高阻接地检测方法主要有时频域法、行波法和人工智能法三种[6-8]。时频域法通过选择合适的滤波算法提取故障特征。在高阻接地故障识别上,时频域法一般是对故障时线路零序电流和零序电压的时域特征值进行分析,以物理特征变化作为识别依据。行波法主要是利用故障发生时的行波折反射和波头极性来进行高阻故障识别,但行波信号微弱通常无法检测,且存在对波速度依赖性强和易受干扰等不足。人工智能法利用人工神经网络、深度学习、专家系统等方法提取高阻接地故障特征并实现故障识别,但存在计算量大、需要训练数据、识别结果不可解释等问题[9-11]。本文采用时频域法,并选择离散小波算法提取零序电流的小波能量熵作为高阻接地的判定指标,并通过仿真试验验证该方法的有效性。
1 小电流接地系统发生高阻接地故障特征
1.1 高阻接地故障特征
1.1.1 故障电流小
由于配电网系统覆盖面广,运行环境复杂,发生高阻接地故障的概率较高。高阻故障较为常见的介质为沙石、草坪和水泥混凝土等[12],这类介质故障过渡电阻较大,故障电流较小。10 kV 配电网系统发生典型高阻接地故障的电流如表1所示。

表1 不同类型介质下高阻接地故障电流Tab.1 High resistance grounding fault current under different types of media A
1.1.2 故障波形随机性强
由于高阻接地点的电弧不稳定,过零点周围接地故障电流的畸变特性是随机的,且介质表面易受天气等因素影响,接地电弧会断续或完全熄灭,故障电流可能突然增大或减小,故无法通过设置电流阈值来判断故障是否发生[9]。
1.1.3 故障波形不对称
接地故障电流正负半个周波的波形不对称。由于高阻接地故障会导致接地电流通过地面流失,因此接地故障电流波形可能会出现失真、峰值降低或脉冲不正常的现象。高阻接地故障还会产生高频分量,相位角也会发生变化,导致故障波形不对称,电压电流波形之间的相位差异常。
1.1.4 谐波含量高,高频分量丰富
随着电弧燃烧,高阻接地故障会逐步形成大量的高次谐波和间谐波,且典型的电弧接地电流的高频分量占比高、易分辩。
1.1.5 故障波形非线性畸变
由于高阻接地的故障电流随机性较大,且含有大量的高频容性谐波电流分量,从而引起故障电流波形畸变。
1.2 高阻接地故障模型及零序电流波形
为研究不同线路类型下高阻接地故障特征,本文搭建了具有6条配电线路的小电流接地系统仿真模型,当4号线路经过渡电阻发生单相接地故障时,故障线路及非故障线路的零序电流如图1所示。从图1可知,零序电流数值较小,在故障初期故障线路与非故障线路的零序电流有较明显的差别,经过1个周期后,故障相电流与非故障相电流大小基本一致,因此很难依据电流大小区分故障线路。
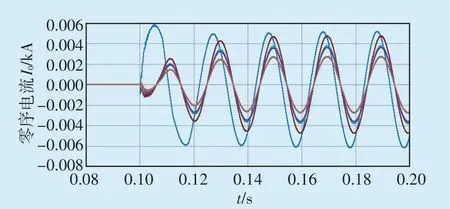
图1 小电流接地系统发生高阻接地故障时零序电流波形图Fig.1 Waveform of zero sequence current in case of high resistance grounding fault in low current earthing system
2 基于小波算法的零序电流故障特征分析
2.1 零序电流的小波分析
连续小波变换可以清晰地将信号特征表现出来,但计算量大。而离散小波变换可以离散化平移因子和伸缩因子,计算出小波变换系数,大幅降低计算量[12]。因此本文采用离散小波变换处理零序电流信号,提取不同频段的小波能量熵作为故障特征量,获取更准确的高阻故障零序电流特征,为后续高阻接地故障检测提供训练样本。
在多分辨率分析小波变换的方法中,故障零序电流会被逐层分解。高通滤波器和低通滤波器的输出成分是占据相同带宽的高频成分和低频成分。每层分解时,采样频率均减半,并对低频分量再次执行上述步骤,生成高低频分量,这个循环执行到设定的分解层数完成为止。以三层小波分解为例,多分辨率分析小波分解流程如图2所示。

图2 小波分解流程Fig.2 Wavelet decomposition process
图2 中,x(k)表示源信号,H(-k)和L(-k)分别为高通滤波器、低通滤波器,↓2 表示采样频率减半。零序电流信号x(k)进行多分辨率小波变换后,可描述为各分量的叠加:
式中:Dj(k)为第j层第k点单支重构下的高频分量,其频带范围为Aj(k)为第j层第k点单支重构下的低频分量,其频带范围为其中,fs为采样频率;m为分解层数。
在进行小波分解的过程中,考虑到高阻故障零序电流信号中包含多个谐波(如五次谐波等),本文采用多频段分辨率和运算速度较大的dbN系列小波进行分解,以db4小波作为小波基函数,提取配电网谐振接地系统的高阻接地故障特征量。分解层数同样会影响计算精度与计算量,若分解层数过多,会造成低频信息的冗余,计算量过大,若分解层数过少,则会导致信息识别精度降低。本文采样频率设置为20 kHz,db4 小波基函数分解层数设置为8层,以使分解后的各分量对应频段涵盖工频至高频振荡分量的频率范围。将m=8 代入公式(1)可知,零序电流信号x(k)与各频段分量Dj(k)满足:
同理可得,高频分量Dj(k)所占的频带范围为低频分量Aj(k)所占的频带范围为
小波分解进行单只重构时信号各层分量的频带范围An如下:
式中:n是小波分解尺度。
参照小波分解结果,将不同支路形成的零序电流分解为9 个db4 小波层后,不同小波系数对应的每一层具备不同的特征。在故障发生后的暂态过程和随后的稳态过程中,各层不同的零序故障电流分量会呈现不同程度的波形变化和幅值,进而能够提取必需的故障信息。
2.2 小波系数的频带能量
将各分支线路零序电流设为初始电流,对零序电流信号进行db4 小波分解,然后采用分解出的小波系数对零序电流信号进行重构,进而对经信号重构后的零序电流信号结果进行叠加后得到:
式中:cDj是第j 层高频分量的重构结果;cAj是第j层低频分量的重构结果;m是分解层数。
将cAj用cDj+1来表示,则由公式(4)叠加后的结果可以记为:
对第j层第k点的值cDj(k)平方后进行求和,得到第j层重构后信号的系数频带能量Ej:
式中:Nj为第j层系数的数据点长度。
计算过程中的每一层小波系数的频带能量都含有零序电流信息。因此,本文使用近似系数能量Ei代替各层系数频带能量Ej,二者在数值上的总和为100。同时,近似系数能量与其他各层细节系数能量和各层总能量之比的总和为1。基于此,可以确定发生高阻接地故障的具体线路位置。
2.3 小波能量熵——故障特征的提取
小波熵是小波分析与信息熵理论的结合,两者相辅相成,不仅可以对突变信号进行多重识别分析,还具有强大的熵信息表征能力,可以更有效地分析信号特征。因此采用小波能量近似计算公式得到零序电流的小波能量熵作为高阻接地故障的识别特征量。将小波系数矩阵沿层数j 和采样点k进行二维展开,得到小波时频熵的定义如下:
根据公式(6)可知,E1,E2,…,Ej,…,Em+1为零序电流经小波分解后各层的能量值,E=∑Ej为各层能量的总和,Pj=Ej/E为各层能量与能量总和的比值,且满足∑Pj=1,该比值可用来描述待分析信号各层能量的分布规律。小波熵Wee可定义为式(9):
与总能量中各层能量值占比相比,小波熵可以准确描述零序电流在每层的能量分布情况,且能够识别接收信号在结构特征上的明显突变。当某一工作频率的能量值占比较大时,小波熵会明显变大。因此本文将零序电流进行小波分解,并根据分解得到的小波熵作为高阻接地故障识别特征量。
3 基于小波算法的小电流接地系统高阻接地故障识别仿真验证
3.1 仿真模型参数设置
为验证本文提出的小波算法识别高阻接地故障的正确性,在PSCAD 仿真平台中搭建10 kV 配电网谐振接地系统仿真模型,采用中性点经消弧线圈接地方式,具体如图3 所示。为保证故障识别方法具有普适性,在仿真模型中设计了多种线路类型,线路1、2 是架空线和电缆的混合线路,线路3、4 是地下电缆,线路5、6是架空线。
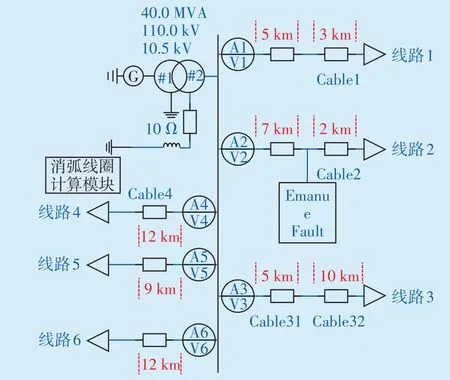
图3 谐振接地系统仿真电路图Fig.3 Simulation circuit diagram of resonance earthing system
输电线路1—6的长度分别为8 km,9 km,15 km,12 km,9 km,12 km。消弧线圈的过补偿度为10%,有功损耗等效电阻百分值取3%进行消弧线圈的参数整定。高阻接地故障选择Emanuel 模型,模型非线性畸变表征能力比较强,在对高阻接地故障识别中得到了广泛应用,其结构如图4所示。
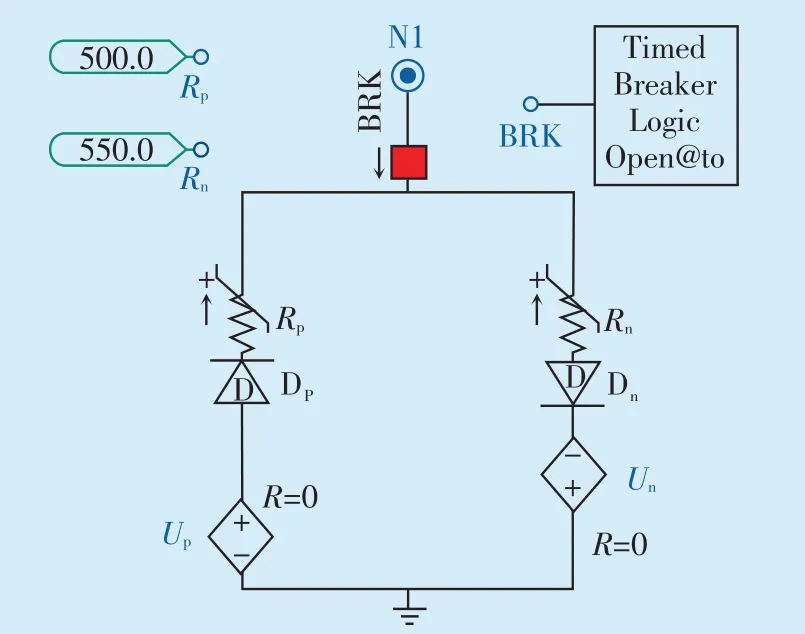
图4 基于PSCAD搭建的高阻故障Emanuel模型Fig.4 High resistance fault Emanuel model built based on PSCAD
为了更好地描述高阻接地故障特征,选择了故障特征最明显的模型参数,具体参数设置见表2。
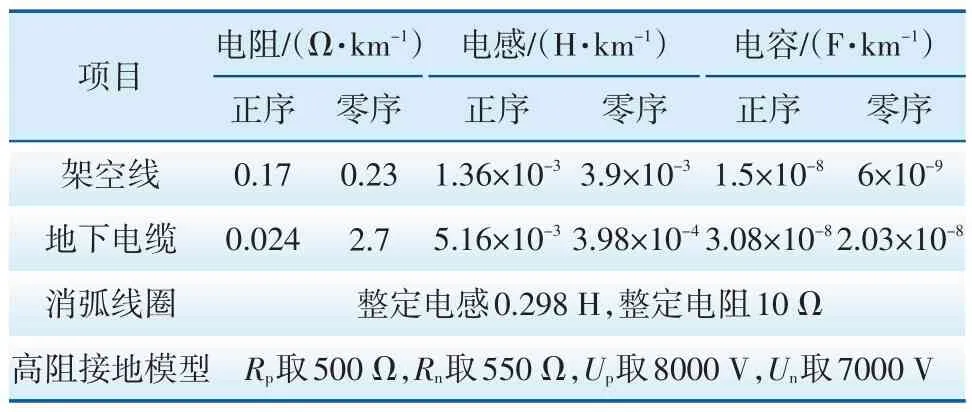
表2 线路仿真模型参数设置Tab.2 Parameter settings for line simulation model
该模型由两个可变电阻RP、Rn,两个直流电源UP、Un和二极管DP、Dn组成。为模拟电弧电阻的非线性特征,RP、Rn应取值不同,通过改变RP、Rn对高阻接地故障电流的幅值和相位进行调节,RP、Rn取值范围在500~5000 Ω;UP、Un表示电弧的不同电压值,其值取决于模型所需的电压值,一般在3~10 kV选择;二极管DP、Dn用于控制电流的通断。
3.2 高阻故障识别仿真验证
当高阻故障发生在线路1时,6条线路的零序电流如图5 所示。故障发生在0.1 s 时刻,故障发生后6条线路均出现零序电流,线路1的零序电流在经过一个周期后和非故障线路的零序电流幅值接近,可见从电流大小上难以区分故障线路。

图5 线路1发生高阻故障6条线路零序电流Fig.5 Zero sequence current of six lines with high resistance fault in line 1
仿真试验中使用db4小波基函数对零序电流进行分解,当高阻故障发生在线路1时,故障线路1和非故障线路2 的零序电流小波db1—db9 分解波形如图6 所示。对比可知,故障线路和非故障线路的小波分解波形的高频部分在幅值以及波形特点有明显的不同。

图6 线路1和线路2零序电流小波分解波形图Fig.6 Wavelet decomposition waveform of zero sequence current for Line 1 and Line 2
通过式(9)计算零序电流的小波熵,故障所在线路的小波熵的计算数值为5.777 7,非故障线路2至6的小波熵分别为2.213 8,2.328 9,2.463 2,2.467 0,2.204 8。故障线路的小波熵数值是非故障线路的2倍以上,可明确识别线路1发生故障。
为进一步验证故障识别算法的准确性,本节将故障位置分别设置在线路1至6上,并计算线路1至6的小波熵,计算结果如表3所示。对比可知故障线路的小波熵与非故障线路的小波熵在数值上有明显的差别,将小波熵作为故障特征判断指标,可以准确识别出高阻故障所在线路。

表3 识别结果Tab.3 Identification results
4 结论
针对小电流基地系统发生高阻接地故障时,继电保护装置难以识别故障线路的问题,本文提出一种基于小波算法的高阻故障识别方法,将零序电流进行分段分解后计算得到小波熵作为故障识别量。通过仿真试验验证故障线路的小波熵的数值明显高于非故障线路的小波熵,当故障分别发生在架空线、电缆线路以及架空线和电缆的混合线路时,本算法均能有效识别故障位置。
