车辆荷载作用下露天煤矿内排土场动力响应特征

朱永东，刘光伟

(辽宁工程技术大学 矿业学院，辽宁 阜新 123000)

内排土场是露天矿采掘剥离废石而来的人工松散堆积体，其具有结构特殊，整体性弱和渗透性好等特点，在长期受到矿山爆破、卡车运输等动荷载影响时，极易引发滑坡[1，2]，严重威胁矿区的安全生产。因此，车辆荷载所激发的振动波在露天煤矿内排土场中的传播特性和滑坡灾害机理研究对内排土场防灾减灾工作意义重大。

车辆荷载区别于现如今研究较多的地震荷载，其作用方式是一种低频且作用时间长的荷载，对边坡的动力响应研究可具体划分为边坡岩土体的动力学响应特性和岩土体自身特性的响应规律两方面。在边坡岩土体的动力学响应特性的研究方面，研究的主要内容包括边坡的动应力、动位移、加速度和动孔压等动力响应量的求解，以及在不同影响因素条件下这些动力响应量的变化规律分析。蔡汉成等[3]借用FLAC研究了多种交通荷载下的岩质边坡动力响应情况。Hung等[4]探究了不同速度下的列车荷载激发的振动波在土体中传播特性。何亮[5]分析了车辆速度、车辆荷载大小等不同参数对土体不同深度的动力响应特征。杨官涛[6]研究发现台阶路面的动位移会随着载重的增加或车速的提高而增大。张平等[7]对简化的岩石边坡模型进行振动台试验，通过实验数据修正了Newmark模型，进而得出了边坡动力下的累积残余位移计算公式。Hong等[8]用波传播中的能量谱密度来研究交通荷载引发地面振动响应的问题。樊秀峰等[9]在研究交通荷载引起边坡的动力响应特征中发现边坡岩土体的振动响应自下坡面到上坡面逐渐减弱，同时发现短距离内的振动衰减更快。简文彬等[10]还发现当循环荷载的最大振幅保持不变时，边坡的动力响应频率与峰值呈现波动变化，存在的强响应频段区间与边坡岩土体卓越周期基本一致，易引起不利于边坡稳定的共振响应。在边坡岩土体特性响应规律的研究方面，刘博等[11]试验分析了循环剪切荷载作用下法向应力、岩壁强度、节理起伏度之间的关系。李文秀等[12]发现填充有疏松饱水粉土及粉细砂的软弱结构面会因震动液化而导致上覆岩土体产生滑塌。简文彬等[13]发现振动荷载的长期作用会使边坡原生裂隙延伸、扩张和贯通，进而增大边坡变形。李论基[14]发现边坡岩土体在重载、低频、低速行驶车辆的长期荷载作用下易产生较大的剪切变形破坏。张友葩等[15]认为长期循环荷载作用下且近极限平衡状态边坡岩土体在滑移中会出现较明显的位移滞回现象。黄诚等[16]分析了水平与竖直向振动作用对边坡动安全系数的影响。

因此，笔者以内蒙古元宝山露天煤矿内排土场为原型，借助MatDEM软件构建内排土场边坡动力响应模型，并将实际监测的地震动数据输入模型中，从而实现了车辆激振边坡的过程，并从不同坡面、不同垂直距、不同水平距和同距不同角度多方面布置了一定数量的监测点，提取了包括PGA和PVA值在内的波形响应数据，以此获得了边坡在地震作用下的动力特性及动力响应规律。成果可加深对复杂条件下车辆振动波在岩土体中的传播特性和滑坡灾害机理的认识，具有重要的科学意义和应用价值。

1 研究区概况

元宝山露天煤矿位于内蒙古赤峰市，季风性气候，夏季雨量集中，一般为230～270 mm，占全年降水量总量的68%，并常以大雨或暴雨的形式出现，容易引发内排土场滑坡和泥石流灾害。

排土层数在15层左右，平台宽度和高度约12 m，台阶的坡角32°～35°。矿区地层以泥质粉砂岩、砾岩、砂砾岩和泥岩为主，地层倾角3°～14°，内排土场土料主要为煤矿剥离的黄褐色细粒土质砂，主要由亚黏土、洪积圆砾以及泥砾组成，作为废弃松散土料堆积在现有地质体上，内排土场土料性质相近。经现场采样和室内试验，获得了内排土场土料的实测力学性质，土料的物理力学参数见表1。

表1 土料的物理力学参数

露天矿区运行的车辆具有载重大、运行速度慢等特点，车辆净重在64.4 t左右，满载重在154.5 t左右，速度通常在30～60 km/h[6]。在元宝山露天煤矿内排土场典型台阶处，DMJS型加速度传感器预埋在车辆经常通过路段中，并利用南京丹陌DM-YB1840型动静态应变测试系统监测与信息采集车辆振动波形，结果如图1所示。

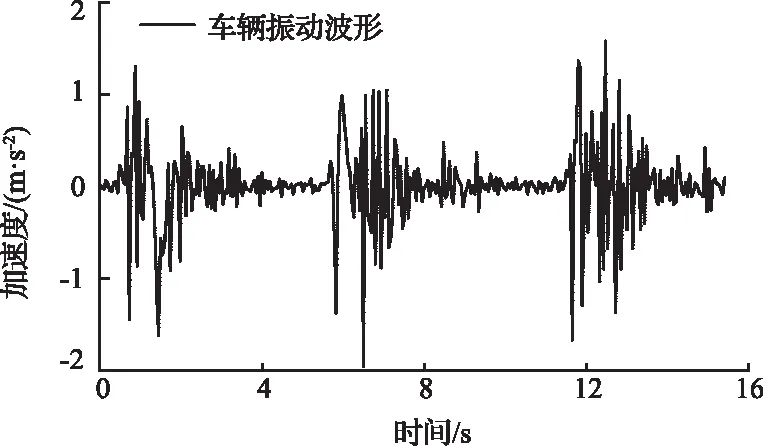
图1 监测设备与结果物

2 数值模拟模型与方案设计

2.1 单元的接触关系

在离散元模型DEM中，土块由许多随机压实的球形单元组成，如图2所示。它们通过易断连接与相邻元素连接，相互作用力仅存在于接触点。单元间的相互作用主要由法向连接的法向力Fn和切向连接的切向力Fs来完成，可以由式(1)和式(2)确定。

Fn=KnXn

(1)

Fs=KsXs

(2)

式中，Kn为法向刚度；Xn为法向相对位移(当两个元素重叠时为负)；Ks为切向刚度；Xs为切向相对位移。

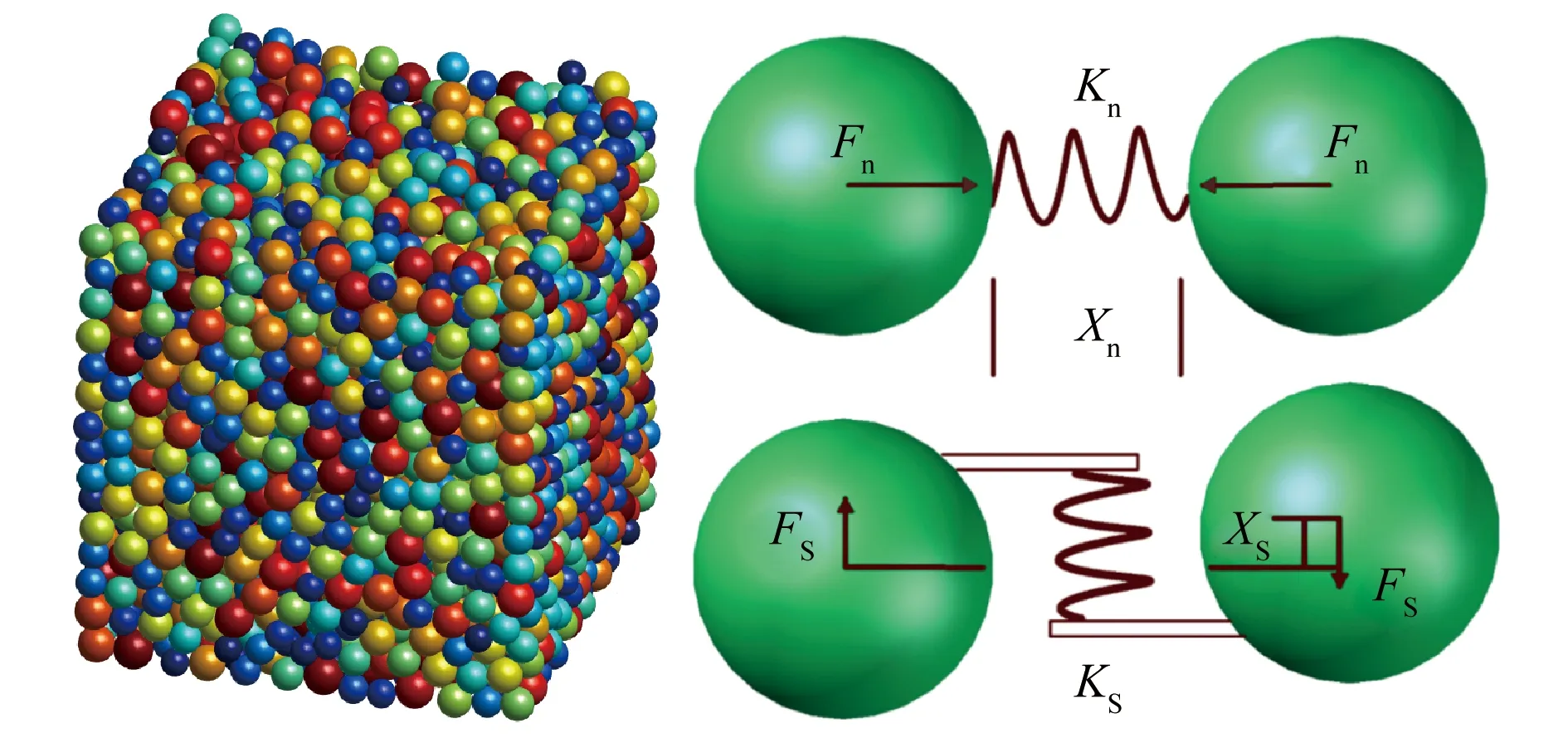
图2 单元堆积与连接

只要Fn或Fs超过相应的限制，两个连接就会断开。例如，Xn超过断裂位移Xb时，法向连接断裂，则一个法向连接所能承受的最大法向力Fnmax为：

Fnmax=KnXb

(3)

法向连接断裂后，即使Xn，两个元件之间也不会产生拉力减小到Xb以下，但无论连接状态如何，压缩力始终存在。因此，断裂连接中的法向力：

同理，剪切力也有其极限Fsmax，可从库仑式方程计算：

Fsmax=Fs0-μpFn

(5)

式中，Fs0初始剪切阻力；并且μp颗粒间摩擦系数。

模拟中的单元所受合力为阻尼力、弹簧力和重力等的矢量和。假设极小时间步中的单元速度和加速度保持不变，并根据牛顿运动方程和时间步迭代算法来实现离散单元的动态模拟[17]。

2.2 内排土场边坡的离散元数值模型

2.2.1 模型中宏、微观参数

土料的实际宏观参数包括杨氏模量(E)、泊松比(v)、密度(D)、抗压强度(Cu)，拉伸强度(Tu)和内摩擦系数(μi)。其中密度和内摩擦系数可直接获得，杨氏模量(E)和泊松比(v)可根据经验获取[18]，由于内排土场的松散土料无法直接测得其抗拉强度，因此，土料的抗拉强度以土的内黏聚力近似替代，抗压强度可通过式(6)[19]获得。

式中，φ为内摩擦角。

最终得到实际宏观参数见表2。

表2 土料的实际宏观参数

在使用MatDEM软件时，模型中的土料需要对应的宏、微观参数，其中微观参数，包括法向刚度(Kn)、剪切刚度(Ks)、抗剪强度(FSo)、断裂位移(Xb)和摩擦系数(μp)。模型中土料的宏、微观参数可先通过相关公式来快速确定，然后经训练优化后获得[20]，见表3和表4。

表3 模型中需对应的宏观参数

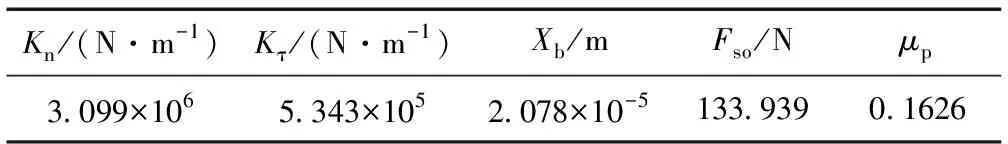
表4 模型中需对应的微观参数

2.2.2 几何模型搭建及监测点布置

根据内排土场剖面模型尺寸采用离散元MatDEM软件切割出约24642个球单元的二阶边坡模型，该边坡模型采用双面坡设计，模型高12.5 m，模型长40 m。其中垫层厚为0.5 m，单个台阶高6 m，台阶坡顶宽6 m，坡底宽15 m，如图3所示。其中单元平均直径约为0.05 m，平均质量约为1.56 mg。将训练后的参数赋值给内排土场边坡模型，即图3(a)蓝色部分。

图3 二维土坡模型及监测点布置情况

本次模拟试验考虑了激发波的不同位置对边坡的影响差异，因此，本试验设计了两种工况，两种工况的激发波形一致，激发位置分别位于一、二级台阶的中部。为研究边坡在地震作用下的动力特性及动力响应规律，在模型边坡的坡表及坡内不同位置处布置一定数量的监测点，以获得动荷载加载过程中的波形响应数据。监测点的布设方案考虑了以下几点：一是以垂直2 m和水平3 m的间隔距分别沿两坡面依次设置监测点1—4、5—8，目的是研究上下坡面对震源波的传播特性和衰减规律的影响；二是以15号监测点为起点并以垂直2 m的间隔距依次设置监测点12—17，以12号监测点为起点并以水平3 m的间隔距依次设置监测点9—11，目的是研究随着离震源的垂直和水平距离的增加，波的传播特性和衰减规律；三是在下坡体内分别以3 m、6 m的直线距离，45°间隔角设置监测点21—26，目的是在动荷载加载过程中提取同距离不同角度下的波形响应数据，包括波的PGA和PVA值，分析波的传播特性。模型共布设了26个监测点，具体布置情况如图3(b)所示。

3 模拟结果与分析

3.1 内排土场边坡中动荷载的波传播特征

工况1、工况2下动荷载激发过程如图4、图5所示。从震源激发波的强弱交替情况，可以看出激发波在模型中的振动情况是基本符合实际检测波形的(图4b、c，图5b、c)。随着震源时间的持续，速度波呈圆弧传播，速度波振幅逐渐衰减(图4a—c)。速度波传递到一定距离后，由于边界基岩、边坡区域的地形起伏和颗粒间的裂缝，振动波会发生一定程度的反射和散射。震源激发的振动波与地基反射波在离基地2 m的水平处形成了首次对冲，其中两股竖向传播分支的波主要表现为抵消作用，水平向传播分支的波则表现为叠加作用(图4d)。模型中多种波的多次叠加或抵消作用导致了波场的无序，波场不再以圆弧特征传播(图4e、f，图5e、f)。

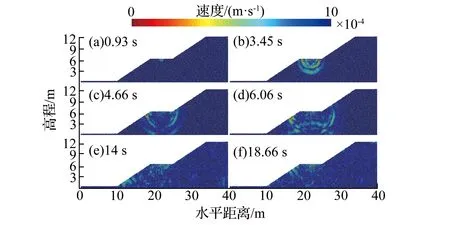
图4 工况1下动荷载激发过程

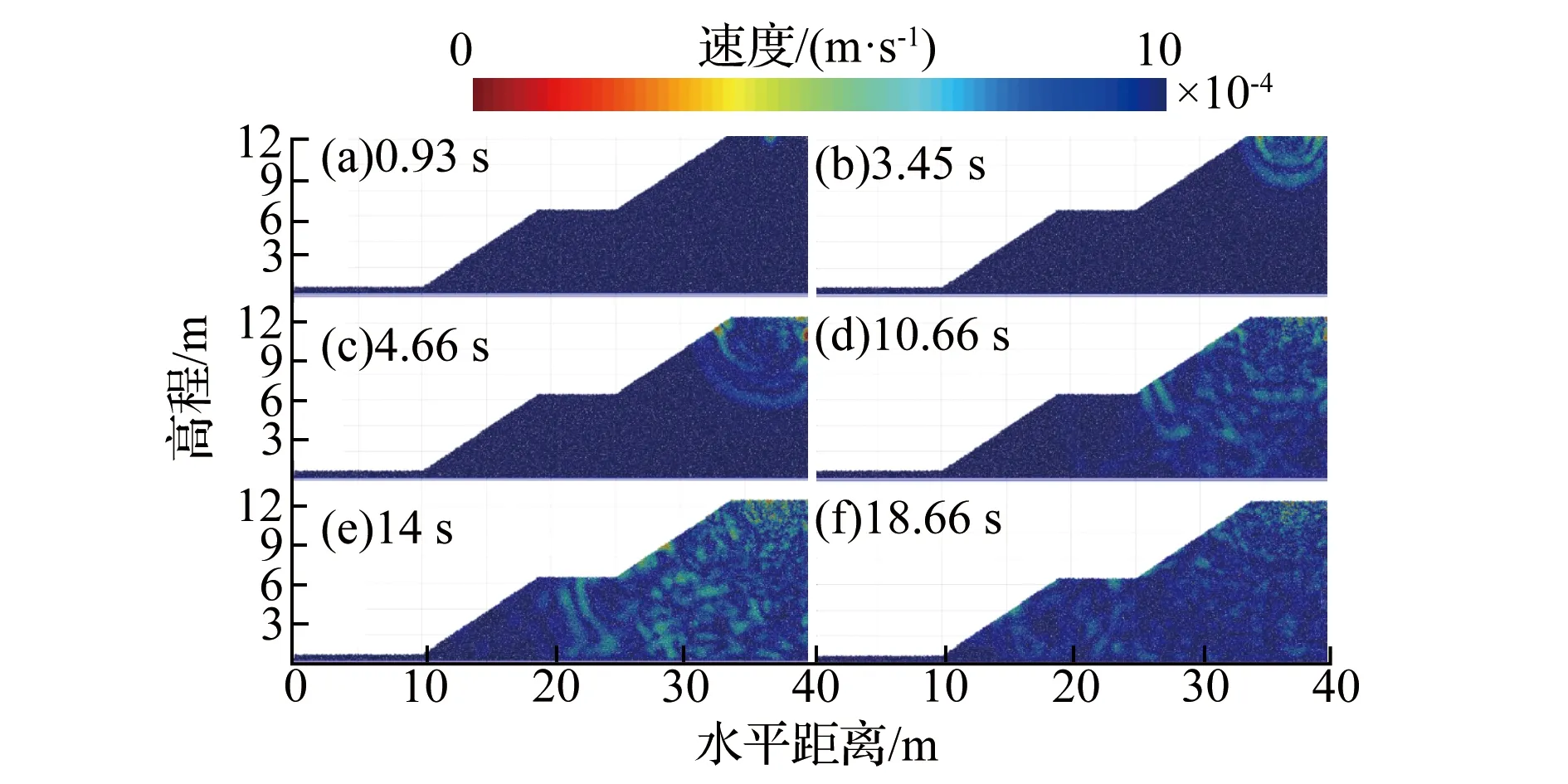
图5 工况2下动荷载激发过程

3.2 动力传递中的波形特征

3.2.1 坡面不同震源距下的波形特征

选取工况1下的上下两坡面监测组(5、6、7、8；1、2、3、4)并提取加速度数据，研究振动波在边坡坡面中的波形特征，如图6所示。随着离震源垂直距离的增加，坡面垂直的加速度波响应时间越慢，振幅和振动频率也逐渐衰减，加速度幅值平均削减了2/3～3/4。在离震源相同的距离下，下坡面的垂直振动波形均比上坡面的强烈，这说明在同等条件下，下坡面相比于上坡面更易聚积能量。这是因为震源激发的振动波传播至下坡面时，振动波得到了一定的累计。从图4的4.66 s也可以看出振动波在遇到锐角的界面时，一是振动波速因受阻降低，从而开始积攒后续的波形能量，二是狭窄界面收缩了波形扩散面，从而开始累计周围的波形能量；遇到钝角界面，情况相反。

3.2.2 坡内不同震源距下的波形特征

选取工况1下的坡内监测组(12、11、10、9、5)和工况2下的坡内监测组(14、13、12、16、17)分别研究离车辆震源不同水平和竖直距离下的波形特征，如图7所示。随着离震源距离的增加，坡面垂直和水平向的加速度波响应时间越慢，水平距和垂直距的两相邻监测点的初始响应间隔时间分别为0.038 s和0.013 s；振幅和振动频率也逐渐衰减，加速度幅值平均削减了3/4。

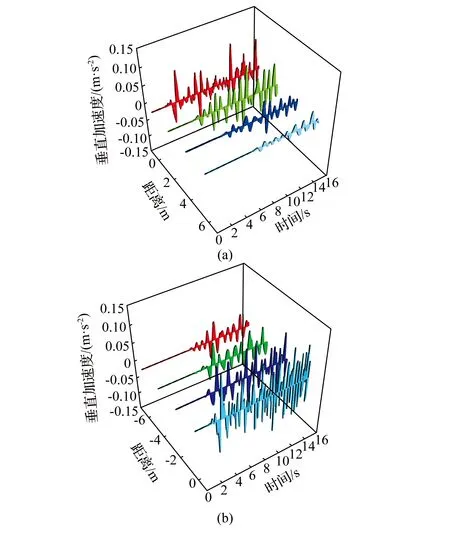
图6 坡面垂直向加速度波形

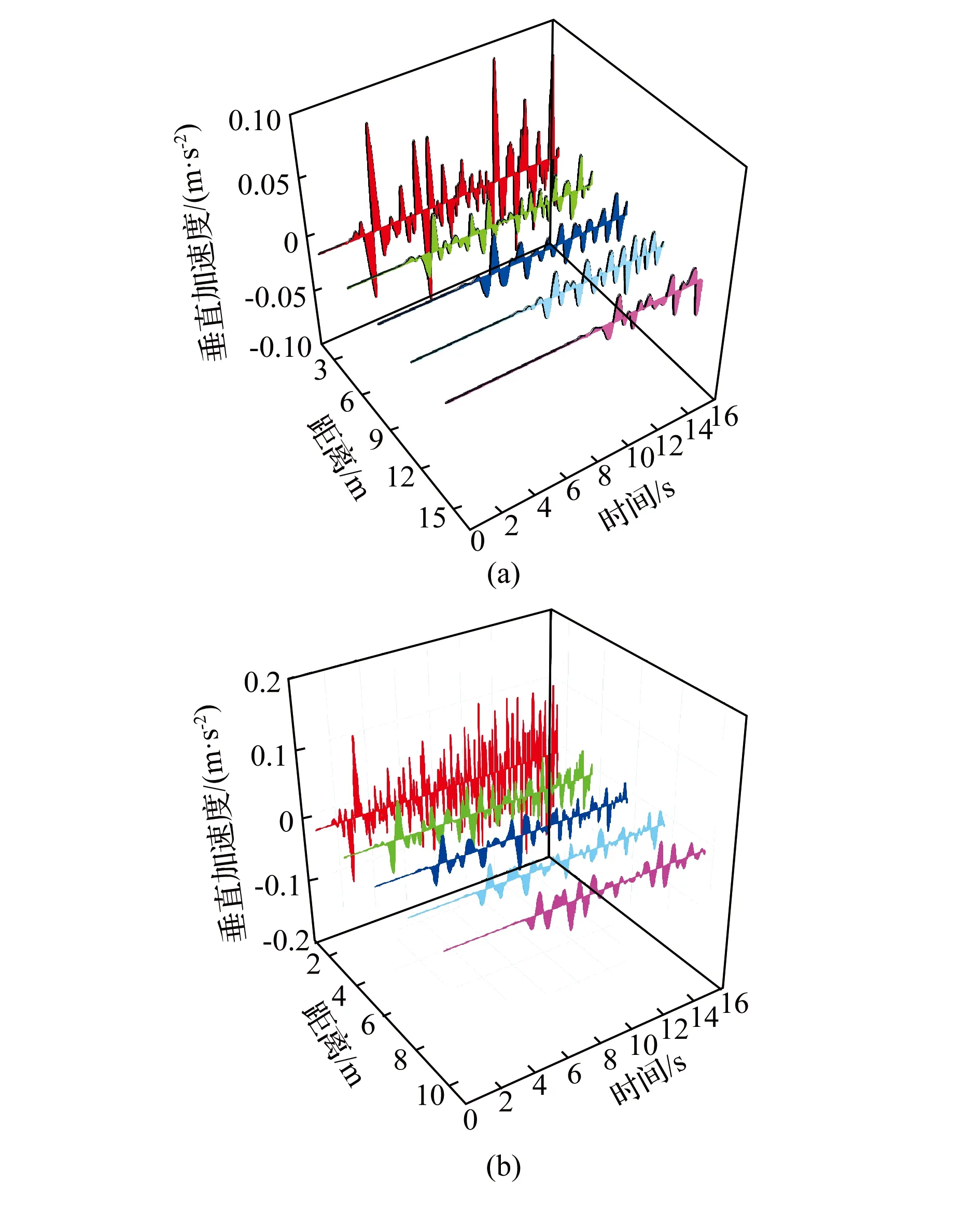
图7 坡内垂直向加速度波形

在同等的波传递效率下，振动波传播距离越远，其垂直和水平向的加速度各项指标均越小。结合图5动荷载激发过程图可知，波在传播中的振幅、频率变化主要受到波传播距离与土密实度的影响较大。其中波传播越远，波扩散面越大，波动能量越分散[21]，土的密实度越大，波的持续传播则需要更多的能量，波损程度则更大。关于地形起伏对波传播的影响方面，地形通常指地面或坡面，而坡面位置的土密实度均较低，土的低密实度则可以解释地质波在坡面具有放大效应；地形的起伏同样影响着波在传播过程中的扩散面，振动波在狭窄界面具有聚波的放大效应，在开阔界面具有散波的缩小效果。

从以上各监测点的波形特征图可以看出，激发波引起的振动波会随着波传递距离的加长，其振动幅值与频率均会渐小，其振动波形也更加圆滑，表现为土粒振动情况越趋于轻缓。通过选取图7(b)中与震源竖向距离最近与最远的14和17号监测点，并按垂直与水平时程曲线呈现其振动趋势的空间轨迹，可较为直观地比较两监测点附加土粒间的振动趋势差异，如图8所示。图8很好地反应出了近震源土粒的振动复杂、混乱与远震源土粒的振动简单、轻缓特点。

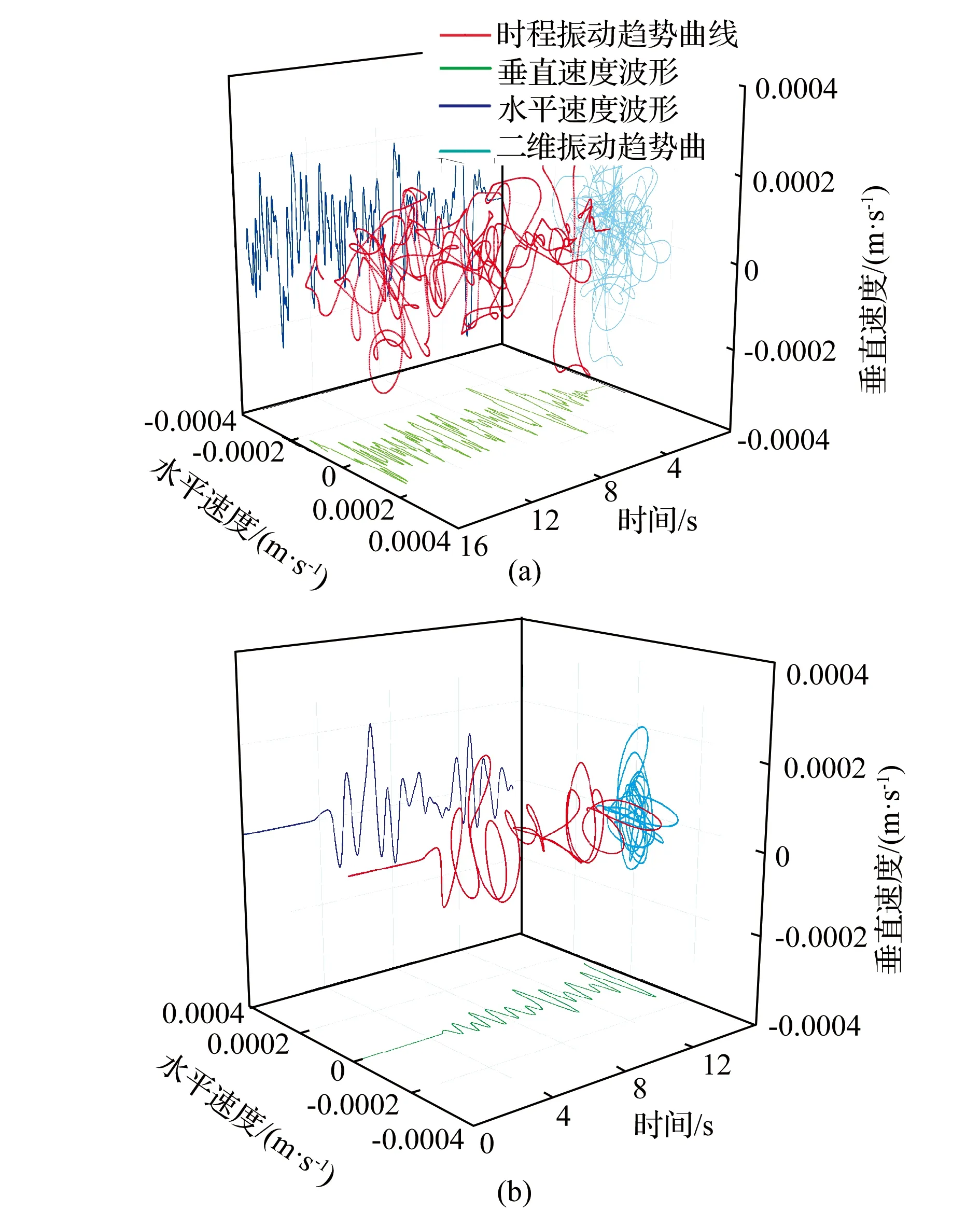
图8 土粒振动趋势

3.3 震源传播特性和衰减规律的影响

3.3.1 不同传播角度下的的箱型统计

图4(d)中的6.06 s显示了振动波在接触基底后进行了波反射，以及后续的振动波在下坡体内的反复叠加和抵消作用使波场更加无序，这无疑影响到了对与震源同距离但不同传播角度下的传播特性和衰减规律研究。为了避免波反射与折射所带来的干扰，只提取工况1下4.66 s之前的加速度数据，并对与震源同3 m距但不同传播角度下的监测点数据进行箱型统计，结果如图9所示。

22监测点垂直向加速度的各项指标均大于21、23和5号监测点，这说明震源垂直向激发的振动波在竖向对垂直波的传递效率最高[22]；23监测点加速度的各项指标均大于21号监测点，这说明在波同等的传递效率与对称位置下，近坡面的振动大于坡内，说明越近坡面越具有放大效应[23]；21号监测点水平向加速度的各项指标均大于22号监测点，而21号监测点附近的土粒更加密实，这说明震源垂直向激发的振动波在斜向对水平波传递效率较高[22]；4号监测点垂直向加速度的各项指标均大于5号监测点，这说明在波同等的传递效率与对称的坡面位置下，沿坡面传播的振动波在锐角界面具有扩大效应，在钝角界面具有缩小效果。

3.3.2 不同震源距下的极值衰减

坡内不同震源距下的极值如图10所示，PGA和PGV随着与震源的水平和垂直距离的增加而逐渐减小，表现出明显的衰减效应。震源产生的振动波影响范围有限，在距离震源3～6 m的范围内对动力响应影响较大，而在距离震源6 m以外的区域影响较小。

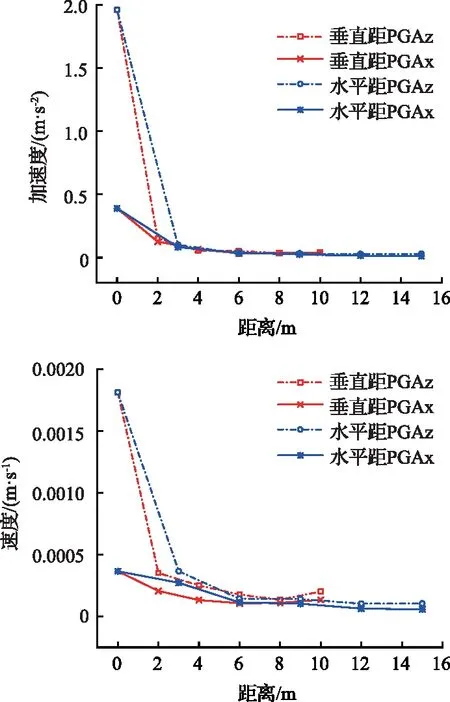
图10 坡内不同震源距下的极值

坡面不同震源距下的极值如图11所示。工况1激发的振动波在下坡面的PGA均比上坡面的大，这是因为一阶边坡的狭窄界面使振动波具有聚波的放大效应，第二阶边坡的开阔界面使振动波具有散波的缩小效果[24]。随着与震源距离的增加，下坡面的3号监测点和上坡面的6号监测点PGA均有增大的趋势，这是因为波形首次对冲与波场无序的中心位置均在震源正下方且高基地2 m处附近(图4d—f)，而对冲中的两股波在竖向传播路径中主要表现为相互抵消，3、6号监测点则处于抵消的影响范围内；在水平向传播路径中主要表现为相互叠加，这使得斜向上的2，7号监测点所处的位置更易受到反射或散射波的增幅。此外，2号监测点因离对冲位置更近而增幅更大。在工况2下，震源激发的振动波与侧边界的反射波相对于上坡面可视为同源振动波。因此，工况2下的8号监测点PGA均大于工况1下的4号监测点PGA。随着与震源距离的加大，上坡面的7号监测点PGA任无增大的趋势，这再次证明了工况1下的反射与散射波对坡面确有增幅的影响。所以，地形起伏情况、界面位置和震源位置均会通过影响波反射与散射的方式而影响坡体的最终PGA值[24，25]。

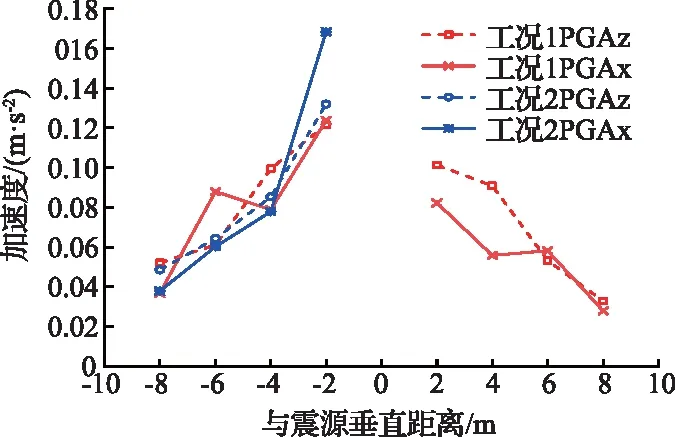
图11 坡面不同震源距下的极值

车辆荷载的较小振幅对内排土场边坡的破坏效果不明显，但人工松散堆积的新进内排土场土料密实度会长期受到车辆荷载的影响。其中，内排土场平台处的大部分土料在车辆的静压力下会逐渐密实，较大约束的坡内土料在车辆振动下也会趋于密实，由于坡面具有放大效应，较小约束的坡肩和坡面土料受车辆振动影响任处于松散状态。

4 结 论

1)震源激发的加速度波呈圆弧传播，因边界基岩、边坡区域的地形起伏和颗粒间的裂而发生一定程度的反射和散射，多种波的多次叠加或抵消作用会导致波场的无序。

2)振动波传播越远，波扩散面越大，波动能量越分散，土体振动的起始时间越晚，振幅和频率越小，表现为土体振动越简单，距震源3～6 m范围内的动力响应较大。途中遇到的土密实度越大，波损程度则越大。

3)振动波在遇到锐角的界面时，一是使振动波速受阻降低，从而开始积攒后续的波形能量，二是收缩波形扩散面，从而开始累计周围的波形能量，坡体内的狭窄界面也由此具有了聚波的放大效应，开阔界面因相反情况而具有散波的缩小效果。此外，越近坡面越具有放大效应，且下坡面相比于上坡面更易聚积能量。

4)地形通常指地面或坡面，而坡面位置的土密实度均较低，土的低密实度则可以解释地质波在坡面具有放大效应；地形的起伏同样影响着波在传播过程中的扩散面，振动波在狭窄界面具有聚波的放大效应，在开阔界面具有散波的缩小效果。此外，地形起伏情况、界面位置和震源位置均会通过影响波反射与散射的方式而影响坡体的最终PGA值。