不同参数对带粗糙冰翼型绕流流场结构影响的实验研究

郑诚毅, 杜旭之, 东乔天, 杨志刚 熊 兵, 徐 毅, 吴凌昊, 金哲岩,

(1. 同济大学 航空航天与力学学院,上海200092; 2. 中国商用飞机上海飞机设计研究院,上海 201203; 3. 上海市地面交通工具空气动力与热环境模拟重点实验室, 上海 201804;4. 中国航发四川燃气涡轮研究院,四川 绵阳,621000)

结冰会改变飞机的气动外形,影响飞机的飞行安全.当飞机飞行在一个低温且湿度大的环境中,未冻结的过冷水滴会撞击飞行器表面,通过质量和热量交换形成冰的吸积.飞机的大部分部件都有可能发生结冰,比如机翼、尾翼、发动机进气口、天线罩等,严重影响飞机的气动性能,危害飞机的飞行安全[1-4].近年来,过冷大水滴 (Supercooled Large Droplet, SLD) 产生的结冰问题越来越受到人们的关注.由于SLD的飞溅、反弹等特殊现象,液滴会越过防除冰系统的极限,形成更容易造成流动分离的冰脊,并导致飞机过早失速[5].粗糙冰是在过冷水滴积累过程中附着在翼型前缘表面,随着时间变化而不断增长的一种特殊冰形.粗糙冰的粗糙度会直接影响到翼型表面的局部对流换热系数和摩擦系数,它们反过来又会影响到最终冰形.除此之外,粗糙冰会显著改变翼型轮廓和表面的无黏流场,破坏翼型表面的附着流并影响翼型整体的气动性能.研究人员已对不同形状的冰形(角冰、流向冰和展向冰)及其对翼型绕流流场的影响做了大量研究,却缺乏对粗糙冰存在时翼型绕流流场的实验研究.因此使用SLD结冰条件下产生的粗糙冰的粗糙度,并且以实验手段来探究粗糙冰对翼型绕流流场结构的影响,对机翼的防除冰设计来说具有重要的研究价值及实际意义.

文献[6-7]中研究了冰的粗糙度特征并将带冰机翼前缘划分为3个主要区域: 光滑区、粗糙区和羽毛区.研究发现即使在结冰产生的早期阶段,粗糙冰的特征高度也大于局部边界层的厚度,对流动产生破坏.文献[8-10]中详细研究了独立分布的冰粗糙元对边界层转变的影响,结果表明边界层会在冰粗糙元后缓慢过渡成湍流边界层.Smith等[11]用具有相同气动效应的均匀沙粒代替冰的粗糙度,发现粗糙元的密度对翼型的气动性能影响不明显.Jackson[12]也研究了冰粗糙元大小和密度对翼型气动力的影响.黄冉冉等[13]对附有流向冰的翼型气动力进行了数值模拟后发现,在流向冰的冰形表面添加粗糙度会明显降低翼型的气动性能.霍西恒等[14]研究发现结冰表面粗糙度很大程度增强了表面的对流换热效果,影响最终结冰冰形的几何特征.常士楠等[15]通过受力分析,确定了水膜、水珠和细流特征粗糙度的大小及其之间的界限划分,发展和完善了结冰表面的粗糙度模型.Mcclain等[16]对过冷大水滴结冰条件下,翼型前缘在短时间内积累的粗糙冰特征高度进行了测量和记录.在各类翼型和叶型关于粗糙度的研究中,有很多学者选择砂纸来代替表面粗糙度进行实验.Milsch[17]采用叶片表面贴砂纸的方法研究了不同粗糙度影响下的二维叶栅损失.Boer等[18]在研究粗糙度的特征高度和在翼型表面分布的位置对翼型最大升力的影响时,使用了砂纸作为研究对象.Dees等[19]使用不同目数的砂纸和规则排布的粗糙度进行了对比研究,结果表明两者在燃气轮机叶片吸力侧的传热和表面摩擦系数方面区别很小.高磊[20]选取了4个型号的砂纸研究了粗糙度量级对压力机叶片总压损失攻角特性和气流折转角的影响.孙爽等[21]使用3种硅碳化物砂纸来实现3种表面粗糙度,研究了表面粗糙度对低压涡轮叶型损失及附面层特性的影响.

雷诺数对翼型气动性能的影响通常随着冰的粗糙度大小而改变.Hoerner等[22]探索了雷诺数对具有前缘粗糙度的NACA0012翼型最大升力的影响,结果表明雷诺数的降低会导致翼型最大升力略微降低.Broeren等[23]研究表明,光滑翼型的最大升力系数对雷诺数和马赫数有很强的依赖性,对于冰翼结构,雷诺数和马赫数对最大升力系数的影响很小.此外,Rafael等[24]在实验条件限制下选取1.5×105到2.8×105范围的雷诺数研究了不同类型的角冰对翼型性能的影响.

现有研究对冰的粗糙度形成机理[6-7]、几何特征[6-7, 14]及其对边界层的影响[8-13]做了解释,对于在实验中如何表征冰的粗糙度也开发了相应的等效粗糙度模型[15].此外,也有学者记录了过冷大水滴结冰条件下冰的粗糙度数值[16].但关于结冰初期粗糙冰对于翼型气动特性影响的研究比较缺乏,已有研究主要以数值模拟的方式来进行,通过风洞实验获得的翼型绕流流场结构数据较少.本文使用粒子图像测速(PIV)技术在风洞中获取翼型绕流流场的信息,并以翼型前缘的粗糙冰的粗糙度和攻角作为控制变量,来探索翼型在过冷大水滴结冰条件下,粗糙冰的粗糙度对不同攻角下翼型绕流流场结构产生的影响.同时还研究了在0° 攻角和特定粗糙冰条件下,雷诺数的改变对翼型绕流流场结构的影响.

1 实验方法

本项研究所开展的流场测量实验是在一个低速直流式风洞内进行的.该风洞具有一个450 mm×450 mm截面的试验段,试验段的四侧为可替换的光学玻璃.该风洞试验段的上游有一个收缩段和相应的整流段,用来提供均匀、稳定的气流.实验所用翼型模型如图1所示,为不锈钢材质的NACA0012翼型,弦长150 mm,展长250 mm,表面经过抛光处理,并通过一系列支撑结构和攻角结构将翼型模型布置在风洞试验段的中心位置.翼型模型前缘黄色部分为安装砂纸的区域,砂纸覆盖机翼前缘直至33.77 mm弦长处.本项研究所采用的实验装置如图2所示.同步器连接照相机、激光器和计算机,计算机通过控制同步器来协调并驱动激光和照相机完成拍摄.导光臂能够将激光器发出的点光源转换成片光源.

图1 翼型模型Fig.1 Airfoil model

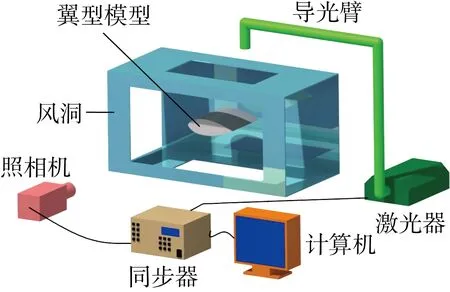
图2 PIV实验装置Fig.2 Experimental facility of PIV

砂纸的表面粗糙度具有弱随机性,在某种程度上与冰的粗糙度达成一致.在现有的等效粗糙度理论支持下,通过多次测量求平均的手段得到的砂纸粗糙度可以表征冰的粗糙度.这在实验中是一种即经济又有效的方式[17-21].Mcclain等[16]的研究表明,在过冷大水滴结冰条件下,弦长为533 mm的NACA0012翼型模型上短时(94 s内)结冰的粗糙元的峰谷差集中在500 μm以下,且分布在距翼型前缘120 mm的区域内.使用表面粗糙度仪器对不同目数的砂纸的垂直方向上的粗糙度(Rz)进行了测量,多次测量求平均值后如表1所示.由于本项研究的翼型弦长为150 mm,通过等比缩放并考虑安装的可行性,最终选择180目、220目、280目和360目砂纸代替粗糙冰进行实验,同时设置没有砂纸的光滑翼型作为对照组.实验所用雷诺数包括8.64×104、1.08×105和1.3×105,实验攻角包括0°、2°、5°、7°、9° 和12°.经测量,在实验所使用的的雷诺数范围内,风洞来流湍流度小于0.5%,满足实验所需精度.下文中以砂纸表征冰的粗糙度均以砂纸的型号表述.

表1 砂纸目数与Rz的关系Tab.1 Relation between mesh of sand paper and Rz

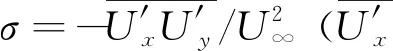
2 雷诺数对R1型粗糙冰作用下翼型流场的影响

取雷诺数Re=8.64×104,1.08×105,1.3×105,使用180目砂纸来代替R1型粗糙冰,在翼型的攻角为0° 的条件下进行实验.探索了雷诺数的不同对翼型绕流流场的流线图、展向涡量和标准化雷诺应力分布的影响.

图3为R1型粗糙冰作用下不同雷诺数的流线图.图中:X为实际流场的横坐标;Y为实际流场的纵坐标;C为翼型弦长.从图中可以看出各雷诺数条件下,气流在翼型前方的流线大体沿来流方向.气流流过翼型上表面的流动以附着流为主,未产生分离.说明实验采用的雷诺数未对气流的流动分离产生明显影响.

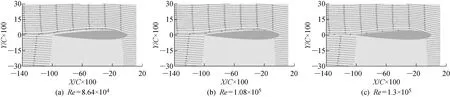
图3 R1型粗糙冰作用下不同雷诺数的流线图Fig.3 Streamline of R1 rough ice at different Reynolds numbers

图4为R1型粗糙冰作用时不同雷诺数条件下的展向涡量图.从图中可以看出涡量在翼型的上表面和前缘并没有产生.正值涡量产生于翼型尾部的上方,负值涡量产生于翼型尾部的下方,形成两条涡量条带.随着雷诺数的增加,涡量条带在X轴方向上的长度显著增加,且愈发清晰可见.流场中其他区域的涡量无明显区别.

图4 R1型粗糙冰作用下不同雷诺数的涡量图Fig.4 Spanwise vorticity of R1 rough ice at different Reynolds numbers

图5所示为不同雷诺数条件下X/C×100=-101 处尾流截面的涡量值对比.从图中可以看出,以翼型弦线为中心,上方的涡量呈现正值,下方的涡量呈现负值,与涡量云图相符.不同雷诺数条件下的涡量值均在Y/C×100=0附近发生了剧烈波动,且Re=1.3×105时涡量的极值明显大于其他两个雷诺数.说明雷诺数不改变该截面处涡量在Y轴方向上的变化趋势,但在一定程度上,雷诺数的增加会使尾流的涡量值增加.

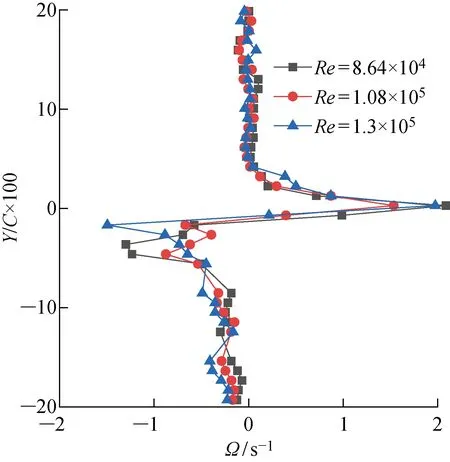
图5 不同雷诺数条件下X/C×100=-101截面的涡量对比Fig.5 Spanwise vorticity comparison of section X/C×100=-101 at different Reynolds numbers

图6所示为Re=1.3×105时R1型粗糙冰作用下的标准化雷诺应力图.从图中可以看出,在翼型的周围无明显的雷诺应力的产生.在实验条件下,不同雷诺数时,流场的标准化雷诺应力分布没有明显的区别.

图6 Re=1.3×105时R1型粗糙冰作用下的标准化雷诺应力图Fig.6 Normalized Reynolds stress of R1 rough ice at Re=1.3×105

图7为不同雷诺数条件下X/C×100=-101 处尾流截面的雷诺应力数值对比.从图中可以看到Re=8.64×104时雷诺应力的波动最为剧烈,其最小值为-0.026,最大值为0.045,均大于其余两个雷诺数条件下的雷诺应力,Re=1.3×105时波动最小.说明雷诺数在翼型前缘覆粗糙冰情况下,影响了该截面处尾流的标准化雷诺应力分布,且随实验雷诺数增大,标准化雷诺应力减小.

图7 不同雷诺数条件下X/C×100=-101截面的雷诺应力对比Fig.7 Normalized Reynolds stress comparison of section X/C×100=-101 at different Reynolds number

3 不同粗糙冰情况下攻角对翼型流场的影响

使用180目(R1型,Rz=158 μm)、220目(R2型,Rz=131.4 μm)、280目(R3型,Rz=119.4 μm)和360目(R4型,Rz= 94.6 μm)的砂纸代替不同的粗糙冰,选取0°、2°、5°、7°、9° 和12° 共6个攻角,在Re=1.3×105的条件下进行实验,同时设置没有砂纸(Rz=0 μm)的光滑翼型作为对照组,探索不同粗糙冰情况下攻角对速度场、展向涡量分布和标准化雷诺应力分布的影响.

图8为0° 攻角时不同粗糙冰条件下的速度场(v).从图中可以看出,速度场以翼型为轴对称分布.翼型前缘处和后缘尾流的速度最小,上翼面表面的速度最大,并向外逐渐减小.不同粗糙冰条件下的速度场分布非常相近,无粗糙冰情况下的尾流相对更加平滑、稳定.

图8 不同粗糙冰条件下的速度场Fig.8 Velocity of different rough ice

表2提取了各粗糙冰作用下翼型上表面气流速度的最大值和该最大值发生处的X轴坐标.从中可以看出,除R3型粗糙冰数据以外,粗糙度的存在降低了流场中气流速度的最大值,且最大值发生的位置也向翼型尾端移动.R1型粗糙冰作用下流场中气流速度的最大值仅为光滑翼型时的90.2%.流场中气流速度的最大值越小意味着流场的平均速度越小,因此翼型上表面压力值也越小.由此可见,粗糙冰的存在会影响翼型的升力,且粗糙度越大,对升力的破坏越严重.

通过对比各粗糙冰作用下翼型绕流流场的展向涡量分布和标准化雷诺应力分布也可以发现粗糙冰使会使尾流流动变得紊乱且具有旋度的流动区域增大.但在所有粗糙冰中,R4型粗糙冰作用下翼型绕流流场分布与光滑翼型最为相近.因此,引入攻角对R4型粗糙冰和光滑翼型情况下的流场进行下一步分析.

图9为光滑翼型和R4型粗糙冰作用下不同攻角的流线图.由图可见,在0° 和9° 攻角下,气流在翼型前方的流线大体沿来流方向.气流流过翼型上表面的流动以附着流为主,并未产生分离.在12°攻角下,气流从翼型前缘往后缘运动的过程中,不再附着在壁面上,边界层发生分离,出现回流并形成了分离泡.图9很好地反映了翼型随攻角增大而产生的流动分离过程.表3所示为分离泡特征表.由表可见,带粗糙冰的翼型气流分离发生在X/C×100=-18处,而光滑翼型发生在X/C×100=-19处,说明粗糙冰会诱导气流提前分离,且提前量为1%的翼型弦长.同时可以发现,粗糙冰的存在降低了分离泡的宽度,带有粗糙冰的分离泡左极限在X/C×100=-121 处,而光滑翼型情况下分离泡左极限在X/C×100=-126 处.结合气流的分离点可以发现,粗糙冰存在时气流会提前产生分离,但整体分离泡的宽度小于光滑翼型情况下.对比两种情况下流线图中分离泡的结构可以发现,光滑翼型的分离泡内流动较规则,而粗糙冰存在时分离泡中心区域的流线有一定程度的波动.

表3 分离泡特征表Tab.3 Feature of separated bubble

图9 光滑翼型和R4型粗糙冰作用下不同攻角的流线图Fig.9 Streamline of clean airfoil and R4 rough ice at different angles of attack

图10为光滑翼型和R4型粗糙冰作用下12° 攻角时的涡量云图.从图10中可以看出,无论有无粗糙冰,正值涡量始于翼型前缘,负值涡量始于翼型尾缘.通过提取数据发现,光滑翼型情况下,涡量的最小值为-5.33 s-1,发生在X/C×100=-103.25截面处;涡量的最大值为8.165 s-1,发生在X/C×100=-4.38 截面处.R4型粗糙冰情况下,涡量最小值为-3.94 s-1,发生在X/C×100=-102.27 截面处;涡量最大值为7.645 s-1,发生在X/C×100=-4.38 截面处.由此可见,粗糙冰的存在对涡量最大值发生的位置没有影响,但略微影响了涡量最小值发生的位置.从涡量最大值和最小值的数值来看,粗糙冰存在时,无论是正值涡量还是负值涡量均小于光滑翼型情况下的具体数值.

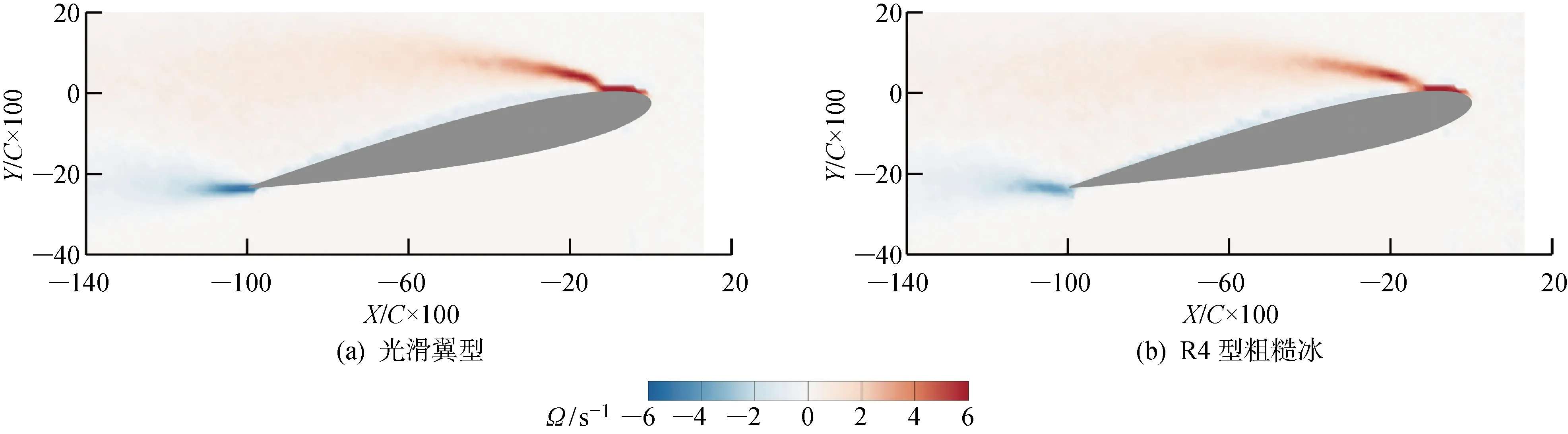
图10 光滑翼型和R4型粗糙冰作用下12° 攻角时的涡量Fig.10 Spanwise vorticity of clean airfoil and R4 rough ice at a 12° angle of attack

图11给出了不同流场截面处,光滑翼型和R4型粗糙冰的涡量值对比.在图11(a)所述截面下,光滑翼型尾流的涡量绝对值明显大于粗糙冰存在时.由图11(b)可见,在X/C×100=-20 截面处两组数据的涡量分布差别不大.由此可见在气流发生大分离的情况下,粗糙冰不改变翼型前缘产生的正值涡量在Y轴方向上的变化趋势:随着Y轴坐标增加,涡量值先略微减小再快速增加,最后快速降到零值.粗糙冰也不会改变翼型尾缘产生的负值涡量在Y轴方向上的变化趋势,但与光滑翼型相比,粗糙冰会使涡量的绝对值减小.

图11 不同粗糙冰流场截面的涡量对比Fig.11 Spanwise vorticity comparison of different rough ices

图12为光滑翼型和带粗糙冰翼型在4个攻角下的标准化雷诺应力分布.从图中可以看出,在攻角为0°、2° 及5° 条件下,粗糙冰对标准化雷诺应力的分布无明显影响.从7° 攻角开始,由于砂纸具有一定厚度且和翼型表面不是平滑过渡,率先产生了应力.在攻角为12° 时,气流产生了大分离,砂纸厚度带来的误差消失,标准化雷诺应力的分布也归于近似.由此可知砂纸的厚度不影响小攻角(0°,2°,5°)和气流产生分离的大攻角(12°)时标准化雷诺应力的分布.

图12 光滑翼型和R4型粗糙冰作用下6个攻角下的标准化雷诺应力Fig.12 Normalized Reynolds stress of clean airfoil and R4 rough ice at six angles of attack

图13为X/C×100=-120处截面的标准化雷诺应力分布对比,可见该截面处标准化雷诺应力的负值区域分布类似,正值区域内在Y/C×100=0附近差别较大,粗糙冰的存在降低了正值区域的雷诺应力.从图9(d)中可见,标准化雷诺应力分布有差异的区域在分离泡与外界层流的交界处.粗糙冰存在导致该处标准化雷诺应力减小,气流流动相较光滑翼型更为平稳,从另一个角度解释了粗糙冰在12° 攻角下会使分离泡的左极限相较光滑翼型更靠近翼型前缘.

图13 X/C×100=-120截面的标准化雷诺应力分布对比Fig.13 Normalized Reynolds stress comparison of section X/C×100=-120

4 结论

探索粗糙冰对翼型气动力的影响对飞机的防/除冰设计来说具有非常重要的价值和意义.目前,对粗糙冰的研究以数值模拟为主,本文使用PIV技术在风洞内获取翼型绕流流场信息,使用砂纸表征粗糙冰的粗糙度.通过改变雷诺数、粗糙冰的粗糙度和翼型攻角,分析了速度场、流线图、涡量分布、标准化雷诺应力分布及相关信息的进一步提取.主要研究结论如下:

(1) 实验使用的雷诺数未对带R1型粗糙冰的翼型绕流流场的流动分离产生明显影响.雷诺数的增加不影响翼型尾流的涡量在Y轴方向上的变化趋势,但会增大尾流的涡量数值.雷诺数影响了翼型尾流处的标准化雷诺应力分布,雷诺数越大则分布越均匀,尾流的流动越平稳.

(2) 带有不同粗糙冰的翼型流场在相同雷诺数和攻角条件下,气流流动的速度最大值随着粗糙度增大而减小,最大值的位置也更靠近翼型尾端,翼型的升力受到的影响就越大.从涡量云图和雷诺应力云图来看,粗糙冰的存在使尾流流动变得紊乱且具有旋度的流动区域增大.

(3) 与光滑翼型相比,在12° 攻角下带R4型粗糙冰的翼型绕流流场中气流提前分离,且提前量为1%的翼型弦长.粗糙冰作用下分离泡的宽度更小,中心位置的流动更紊乱.从涡量云图和标准化雷诺应力云图来看,粗糙冰不影响12° 攻角下涡量和雷诺应力在Y轴方向上的变化趋势,但降低了相应的数值,解释了粗糙冰作用下分离泡宽度更小的原因.