考虑地震攻击交通网影响的配电网韧性评估及提升策略

颜文婷, 杨 隆, 李长城, 罗 伟

(1. 广西大学 电气工程学院,南宁 530004; 2. 国网湖南省电力有限公司超高压变电公司,长沙 410007)

近年来,国内外地震灾害频发,给人们的生命财产带来极大的威胁.配电网在突发性强、破坏性大的地震灾害下易损性较高,主要表现为电力设备在地震发生的短时间内遭到大规模破坏[1-4].因此,构建具有抵御灾害能力的配电网十分必要.通常,网络拓扑结构灵活多变的配电网[5]可以通过调整自身的拓扑结构以及运行方式有效应对小概率极端自然灾害.

韧性评估指标被用于衡量配电网应对极端自然灾害的抵抗能力及灾后快速恢复能力[6-8].文献[9-10]中分别从自然灾害发生的随机性、影响程度和故障的不确定性等方面构建配电网韧性评估指标.文献[11]中考虑网架重构和灾区复电过程,构建吸收率、适应率和修复速率的韧性三角指标.文献[12-13]中以系统功能曲线的缺失面积定义配电网韧性.文献[14]中针对地震灾害,从鲁棒性、快速性和冗余性3方面构建海岛综合能源系统的韧性评估指标.然而,地震灾害可能导致大面积交通网损坏,影响抢修资源的调度[15],上述研究提出的韧性评估指标均未考虑交通网受损的影响,因此可能导致韧性评估结果不够客观.

为提升配电网韧性以应对极端灾害攻击,可分别研究灾前、灾时、灾后阶段对应的韧性提升措施.针对灾前规划防御阶段,文献[16]中提出线路加固和储能配置相结合的配电网韧性提升方法.文献[17]中分析地震灾害时灾前抵抗阶段与灾时降额阶段配电网韧性,但未考虑灾后恢复阶段的韧性提升措施.灾后恢复阶段主要考虑应急抢修资源优化调度和协同多源恢复以提升配电网韧性[18].文献[19]中根据灾后配电网故障特点,提出基于重构及非重构孤岛的微网差异化恢复运行方法.相较于单个微网,文献[20-22]中考虑多微网的协同作用,有效增强配电网韧性.不同于微网,分布式电源具有灵活度高、响应快等优点[23],因此文献[24]中提出接入分布式电源提升配电网韧性的策略.由于移动应急资源的调度受交通网影响,所以文献[25]中研究了灾后网络重构与移动式储能优化调度的策略以提高故障恢复速度.文献[26-27]中协同分布式电源或移动应急电源恢复失电负荷,加快灾后配电网恢复速度.但上述研究均未考虑受损交通网的影响,不适用于地震灾害后的恢复工作.文献[28]中在应急资源调度中考虑受损交通网影响,但在抢修过程中未考虑受损道路清理过程.实际情况下,地震灾害容易引发大量道路中断,如何从受损交通网的角度考虑应急资源调度与故障负荷恢复,还需进一步研究.

针对上述问题,在地震灾害破坏交通网与配电网背景下,提出考虑地震攻击交通网影响的配电网韧性评估指标及灾后韧性提升策略.首先,根据地震峰值加速度建立地震灾害下配电网和交通网的易损性模型,分析配电网线路与交通网道路的故障概率,模拟构建地震灾害场景集.其次,引入配电网抢修队等待道路修复疏通时间,提出地震灾害下配电网韧性评估指标.再次,提出同时考虑故障线路抢修、道路疏通以及应急资源调度的配电网恢复策略,以提升地震灾害下配电网韧性.最后,以12节点交通网与IEEE33节点配电网耦合算例验证所提方法的有效性.

1 地震灾害下交通-配电网故障概率分析

地震灾害发生后,交通网与配电网都将受到不同程度的损坏,例如架空电线杆倒塌造成配电网线路损坏,道路损坏造成交通网受损从而影响抢修资源的调度等.一般而言,电线杆、线路和道路的受损概率与地震等级和离震源中心的距离直接相关.因此,可以拟合地震多发区域的电线杆与道路所在位置的地震动峰值加速度(Peak Ground Acceleration, PGA)来计算电线杆与道路的受损概率[29],用于模拟地震灾害场景,表示为

lgVPGA=

a1+a2M+a3lg[ds-k+a4exp(a5M)]

(1)

式中:VPGA为地震动峰值加速度;M为地震动强度;ds-k为震源与场地的距离;a1、a2、a3、a4、a5为模型系数.

1.1 地震灾害下配电网故障模型

地震灾害下,配电网线路的损坏主要由电线杆倒塌率决定,即地震中电线杆承载力达到或超过倒塌极限值的条件概率,如下所示:

(2)

式中:P(C|M=x)为电线杆在给定的地震动强度M=x下发生倒塌的概率;φ(·)为标准正态累积分布函数;θ为倒塌强度中位数,即结构倒塌概率为50%时对应的地震动强度;β为地震动强度指标的标准差,反映采用不同地震动记录计算结果的离散性.

θ和β计算如下:

(3)

(4)

式中:K为地震动记录的个数;VPGA,b为第b次地震发生对应地震动峰值加速度的值.

线路正常运行的必要条件是该线路段上的电线杆均处于完好状态.因此,线路段故障概率为

(5)

式中:Pi为配电网第i条线路发生故障的概率;m为线路段中电线杆的数量;Pk为线路段中第k个电线杆发生故障的概率.

1.2 地震灾害下道路易损性模型

对比分析已有的地震灾害资料[30],将道路受损程度分为道路完好、轻微受损、中度受损、严重受损、完全毁坏5个等级,主要特征如附录表1所示.

表1 不同的韧性指标比较Tab.1 Comparison of different resilience indicators

道路易损性分析是将道路划分为若干个单位长度的路段,计算各路段峰值加速度,并确定路段易损性函数来计算路段受损概率.单位路段受损概率服从正态分布,单位长度路段在VPGA,k下不同破坏程度对应的概率为

(6)

式中:VPGA,k为电线杆k开始发生倒塌时地震动峰值加速度的值;cl为第l条道路受损程度均值,其标准差取常数ζ.因此,事件E1、E2、E3、E4、E5的概率分别为

(7)

式中:E1、E2、E3、E4、E5分别表示道路完好、轻微受损、中度受损、严重受损以及完全毁坏.

2 地震灾害下配电网韧性评估

2.1 典型配电网韧性曲线

典型的配电网韧性评估包括抵御灾害能力和故障恢复能力两方面,如图1所示.图中:S(t)为配电网的功能函数;t0为灾害发生的时刻;t1为灾害对系统的影响最大的时刻;t2为故障开始抢修的时刻;t3为所有负荷复电、系统开始正常运行的时刻;A1～A4分别为配电网系统韧性曲线的各区域面积.

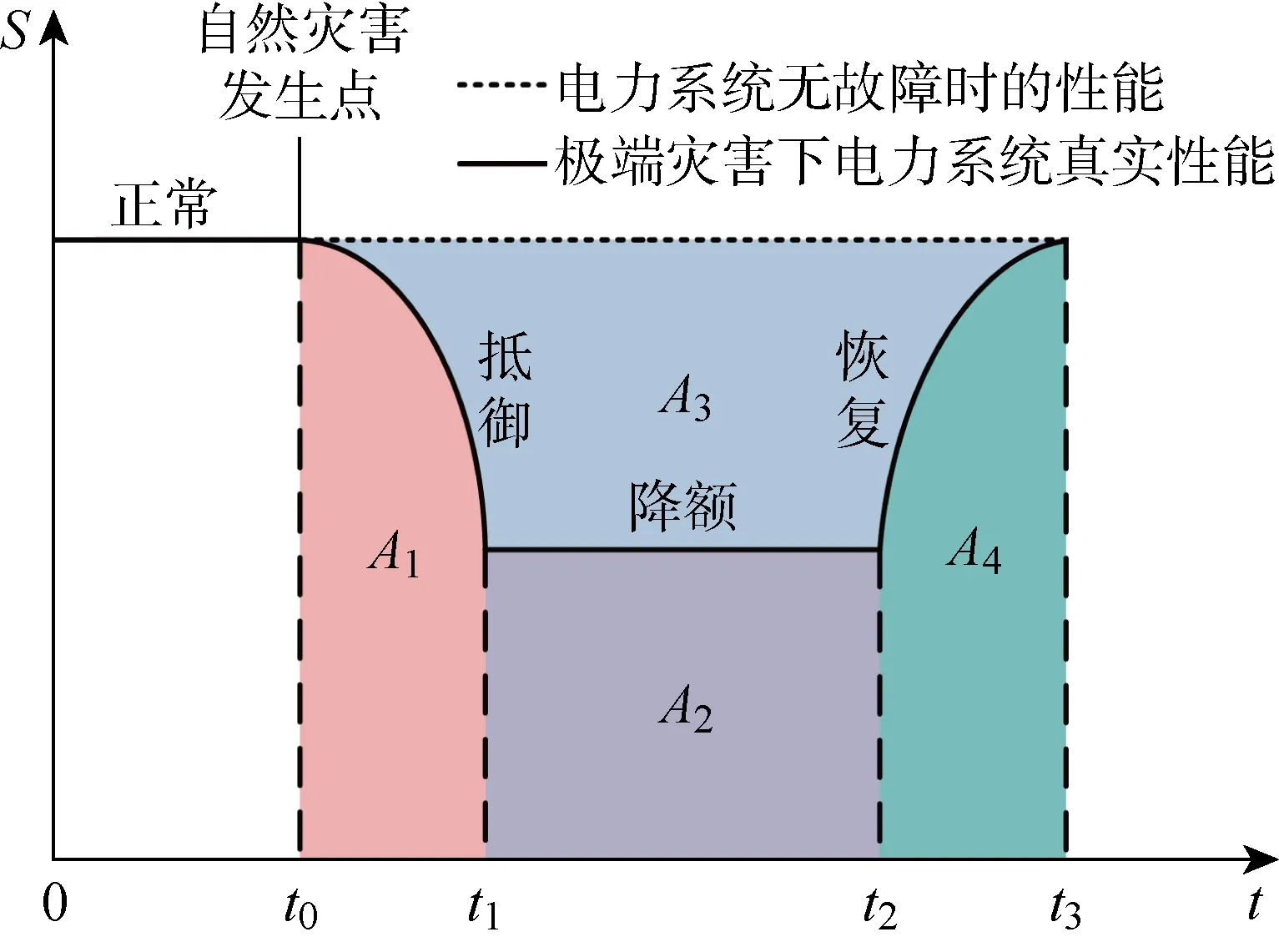
图1 配电网系统韧性曲线Fig.1 Resilience curve of distribution network

2.2 地震灾害下配电网韧性评估指标

与台风、冰灾等极端天气灾害不同,地震灾害持续时间较短,却对配电网破坏程度更高.在故障恢复过程中,地震灾害导致的交通网受损会影响抢修队的抢修进度以及应急资源调度.因此,在传统配电网韧性评估的基础上考虑抢修队等待道路修复疏通时间,提出配电网韧性评估指标,表示为

(8)

式中:Pf、Pl分别为配电网、交通网故障场景的概率;F和L分别为配电网中线路故障和交通网中道路故障的场景数目;tw为配电网抢修队等待道路修复疏通时间.Rn的取值范围为0～1.当tw=0时,说明交通网不影响配电网抢修进程;tw越大,受损交通网对配电网抢修的消极影响越大、抢修速度越慢,从而导致配电网在地震灾害下韧性越低.由于地震对配电网的影响是瞬时的,t0～t1的时间非常短,所以在考虑韧性时可忽略图1中A1的面积.

2.3 计及交通的配电网地震灾害下韧性评估流程

地震灾害期间,线路断线、输电塔倒塌等事故造成电网拓扑结构不断变化,各元件故障概率和系统的状态也随外界影响的变化而变化.同时,道路的损坏也会影响后续的恢复过程.因此,地震灾害下考虑交通网影响的配电网韧性评估是随地震影响状态不断更新迭代的过程,其流程图如附录图1(a)所示,具体步骤如下:

步骤1输入地震灾害强度以及配电网与地震震源中心的距离、配电网各线路的故障概率、交通网各道路的故障概率以及配电网和交通网的基本数据.

步骤2通过轮盘赌算法生成地震灾害下配电网故障场景集、产生各场景的概率以及各故障点修复时间,具体流程详见附录图1(b).

步骤3利用轮盘赌算法生成地震灾害下交通网故障场景集、产生各场景的概率以及各道路修复清理时间.当道路完全毁坏时,则认定道路无法修复清理,需进行灾后重建,即假设修复清理时间为无穷大,具体流程详见附录图1(c).

步骤4分别选定配电网、交通网故障场景,更新该场景下配电网故障线路、故障修复时间、交通网故障道路、道路修复清理时间以及配电网停电区域.

步骤5根据灾后恢复策略模型,生成配电网恢复策略.并根据优化恢复策略对配电网进行修复,具体流程详见附录图1(d).

步骤6更新配电网、交通网场景,重复步骤4～6直到配电网、交通网场景集全部场景模拟完成.

步骤7更新系统状态,利用式(8)计算配电网地震灾害下韧性指标.

3 地震灾害下配电网韧性提升策略研究

为加快灾后故障配电网恢复速度,提升灾后恢复阶段配电网应对地震灾害的韧性,考虑采用协同故障线路抢修、道路修复疏通以及应急资源调度的恢复策略,建立地震灾害下配电网韧性提升的双层优化模型.

3.1 上层优化模型

3.1.1目标函数 上层优化模型包括配电网故障抢修策略优化以及应急资源调度两方面.其中,故障抢修策略通过优先恢复重要负荷和大负荷,减少配电网损失电量.应急资源调度通过应急电源车对配电网重要负荷供电,提高配电网地震灾害下韧性.同时,充分发挥应急电源车的灵活性,为重要负荷供电,协调配电网故障抢修与应急电源车,最大程度减少配电网在地震灾害中损失电量.上层优化模型考虑抢修车、应急电源车的行驶时间、负荷量、负荷重要性等因素构建使配电网失电量最小化的目标函数:

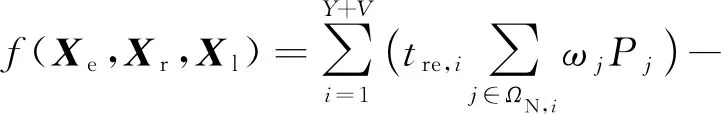
(9)

式中:Xe为配电网故障线路抢修顺序;Xr为交通网故障道路修复清理顺序;Xl为应急电源车调度方案集合;tre,i为第i条故障线路从故障到恢复所需要的时间;ΩN,i为第i条故障线路恢复前,配电网失电节点集合;ωj为负荷权重系数;Pj表示负荷j的有功功率;Y和V分别为配电网故障线路数与配电网联络线数量;D为应急电源车供电的停电区域数量;tpe,r为应急电源车为第r个停电区域供电时间;Ωr为第r个停电区域内应急电源车供电节点集合.

3.1.2约束条件

(1) 拓扑约束.

配电网需要在辐射网状结构下运行,因此定义两个状态变量αaj和ρa,j,建立树模型,从而保证潮流流向变化不影响配电网辐射状运行.

(10)

式中:αaj和αja为0-1状态变量,当电流从节点a流向j时,αaj值为1,αja值为0;当电流从节点j流向a时,αaj值为0,αja值为1;μa为流入节点a的电流矢量和;ρa,j为0-1变量,表示节点a、j之间开关的闭合断开,当开关闭合时,其值为1;断开时,其值为0;Λ为所有线路集合;H为配电网系统开关总数;Ω为配电网所有节点集合.

(2) 负荷约束.

地震灾害发生后,应急电源车对停电区域进行供电.当恢复负荷量较大时,考虑切除可控的普通负荷,保证重要负荷供电的调控.应急电源车的负荷约束为

(11)

式中:κr,j为0-1变量,当应急电源车能够维持节点j供电时,其值为1;否则按照负荷重要程度进行负荷削减,其值为0;PE为应急电源车最大输出功率.

(3) 容量约束.

由于应急电源车容量受限,当应急电源车进行下一步调度时,必须满足对停电区域供电需求,保证该停电区域负荷正常恢复.其约束为

(12)

式中:Eloss为应急电源车行驶损耗能量;Etotal为应急电源车总能量.

(4) 潮流约束.

(13)

式中:Qj(t)为节点j上注入的无功功率;Gaj和Baj分别为节点a和节点j之间支路的电导和电纳;ωaj(t)为节点a和节点j的电压相角差;Uj(t)和Ua(t)分别为节点j和a在时间段t内的电压幅值,且

Uj,min≤Uj(t)≤Uj,max, ∀j∈Ω

(14)

式中:Uj,max和Uj,min分别为节点j上电压幅值上、下限,分别取额定电压的1.05倍和0.95倍.

(5) 故障线路恢复时间.

tre,i主要包括故障抢修时间、抢修车行驶时间以及配电网抢修队等待时间.因此,tre,i可表示为

(15)

式中:ts,i为抢修队抢修第i条故障线路的时间;di为上一条故障线路到第i条故障线路的距离;ε为交通网因地震损坏后轻度受损道路对车辆行驶速度的影响系数;v为抢修车在交通网正常时的行驶速度;tw,i为抢修队抢修第i条故障线路因中度或严重受损道路修复疏通所需要的等待时间;to,i为联络线接通需要的时间;ΛY和ΛV分别为故障线路和联络线的集合.

(6) 应急电源车供电时间.

tpe,r可由应急电源车调度后配电网故障恢复时间之和与应急电源车行驶速度计算得到:

(16)

式中:Λr为配电网抢修队从第r-1个到第r个应急电源车供电区域内故障线路完成恢复期间,待恢复配电网故障线路的集合;dr为上一个应急电源车接入点到停电区域r应急电源车接入点的距离.

(7) 配电网故障线路修复累计时间.

故障线路累计恢复时间可由每条故障线路恢复需要的时间表示,具体如下所示:

(17)

式中:tev,i(Xe)为配电网故障抢修顺序为Xe时,前i-1个故障线路恢复时间的累积.

3.2 下层优化模型

3.2.1目标函数 为提高配电网故障恢复效率,下层优化模型考虑对故障道路修复疏通进行优化,构建使配电网抢修队等待道路修复疏通时间总和最小化的目标函数:

(18)

式中:tw(Xr,Xe)为抢修队等待道路修复疏通时间总和.

3.2.2约束条件

(1) 抢修队等待时间.

当配电网线路抢修与道路清理同时进行时,tw,i可表示为

tw,i=

(19)

式中:trd,i(Xr)为道路修复疏通顺序为Xr时,故障线路i抢修途中遇到的受损道路及此前受损道路修复时间的累计.

(2) 受损道路修复累计时间:

(20)

式中:Z为中度、严重受损道路数量;τz,y为0-1变量,若受损道路z与故障线路y关联,其值为1,否则为0;tz,y为破损道路z每千米道路修复时间;dz为受损道路z长度.

3.3 双层模型求解

在双层优化模型中,上、下层优化模型控制各自的决策变量,从而优化目标函数.上层模型将优化的配电网抢修顺序Xe和故障线路抢修时间tre传递给下层模型,下层模型基于上层优化策略求解出交通网道路修复疏通顺序Xr和抢修队等待道路修复疏通时间tw后,将下层模型的tw与Xr传递给上层模型.配电网和交通网抢修队的行驶路径采用经典弗洛伊德算法求取最短路径.上层模型通过下层优化模型反馈结果,更新配电网抢修顺序Xe以及故障恢复的总时间tev,如此循环到结果收敛或者达到设定的最大迭代次数,求出配电网故障抢修、交通网道路修复疏通以及应急资源调度协调优化策略,具体模型求解流程如图2所示.

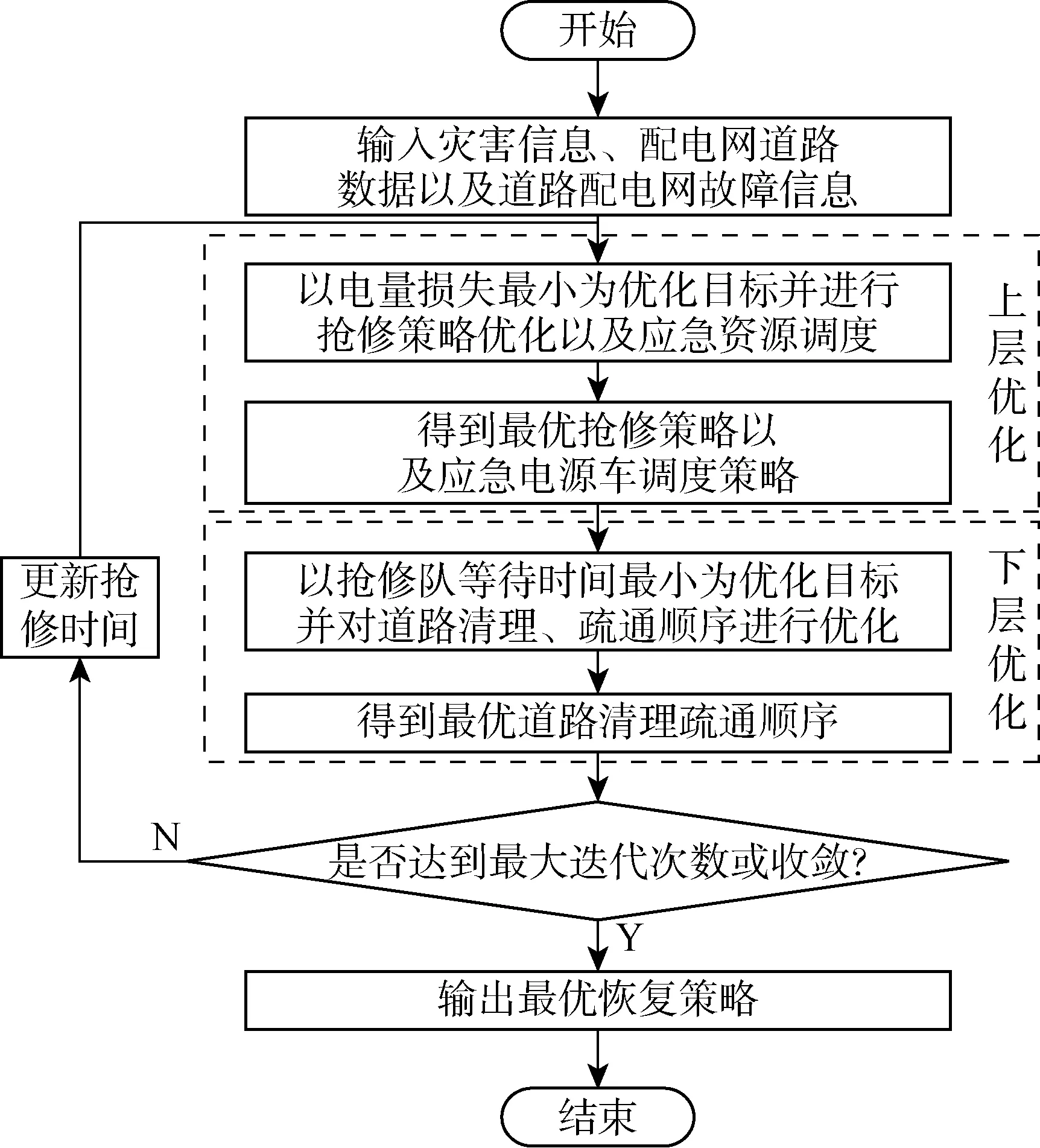
图2 双层优化模型求解流程图Fig.2 Flow chart of solving two-layer optimization model

4 算例分析

4.1 交通-配电网耦合算例

采用IEEE33节点配电网[5]与一个仅考虑城市主干道的12节点交通网[31]相耦合的系统进行算例分析,分别如图3与图4所示.图中:R和#分别表示交通网道路和配电网线路编号.交通网和配电网空间耦合关系如附录表2所示.

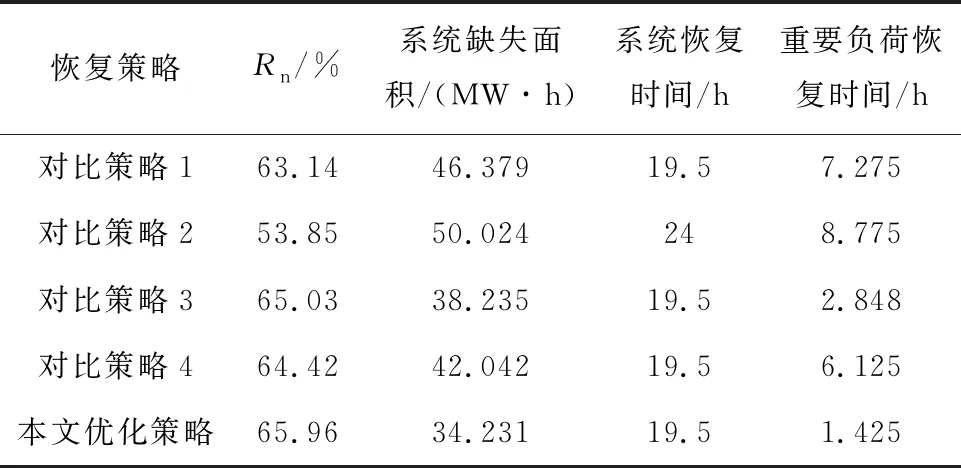
表2 不同策略韧性指标比较

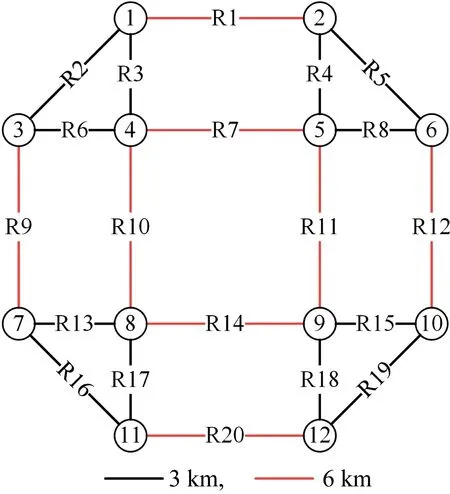
图3 12节点交通网结构图Fig.3 12-node transportation network

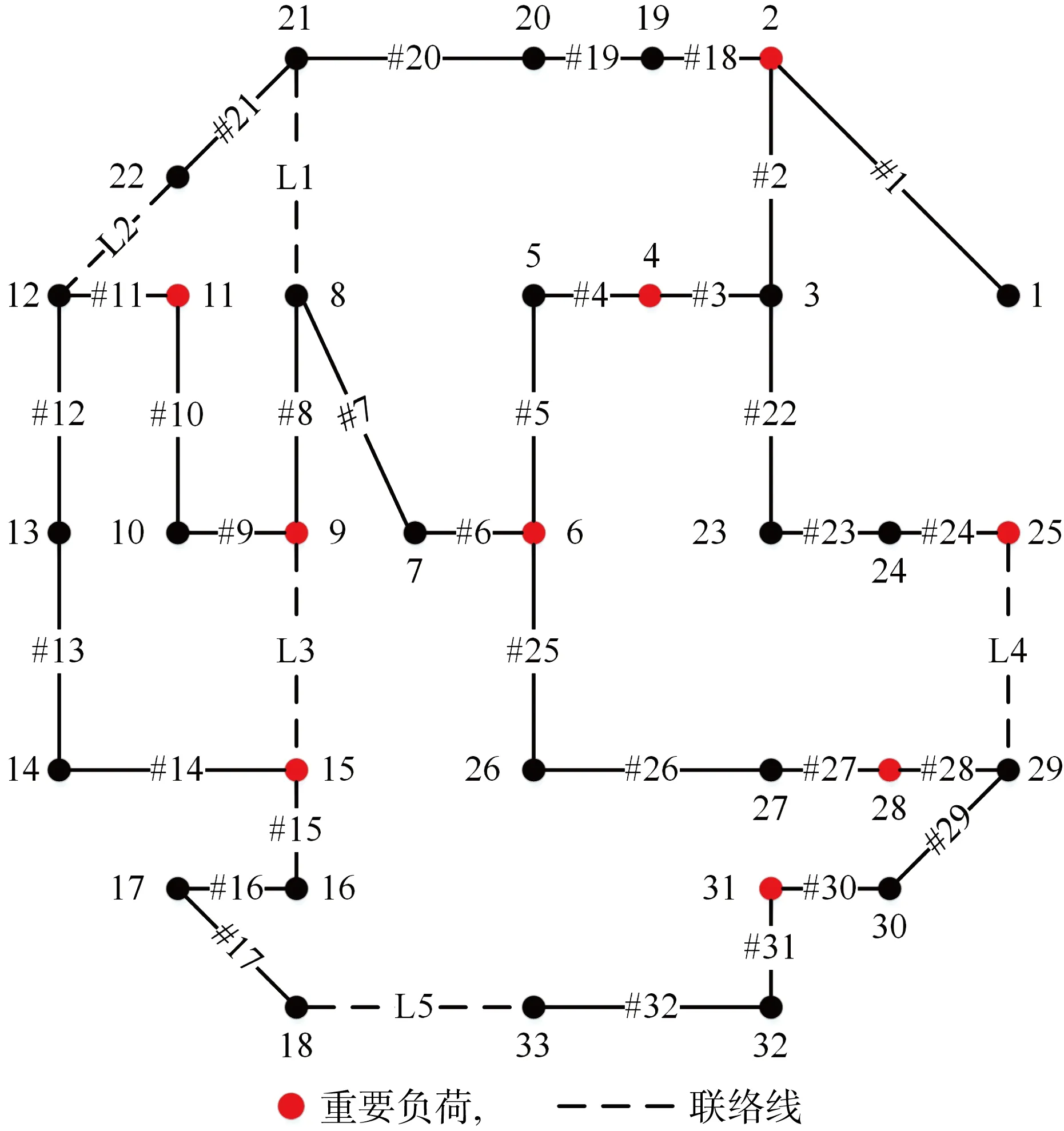
图4 配电网IEEE33节点结构图Fig.4 IEEE 33-bus distribution network

4.2 地震灾害下交通-配电网故障场景分析

4.2.1交通-配电网易损性分析 根据某西南地区地震相关数据统计结果,对式(3)中的θ、式(4)中的β及式(6)中的cl和ζ进行同步估计.配电网电线杆和交通网单位长度道路段受损概率随地震强度、离震源中心距离的变化趋势如附录图2所示.电线杆受损概率和道路受损概率均随地震等级的增大而增大,随震中距的增大而减小.其中受损道路状态表明,在地震情况下,道路轻微受损的概率最大,完全毁坏的概率最小,远小于0.1.在地震灾害下,本文采用的交通-配电网耦合算例故障概率需满足上述规律.

4.2.2交通-配电网故障概率分析 假设交通-配电网系统所在区域发生6.5级地震,震源中心位于交通-配电网耦合系统左侧.将交通-配电网系统划分为8个区域,其中离震源中心距离最近为5 km,最远为12 km,具体划分范围如附录图3所示.为简化计算,对于跨区域的线路,取其中点所在的区域作为计算故障概率的参考点.因此,该场景下配电网各线路、交通网各道路的故障概率分别如图5与图6所示.

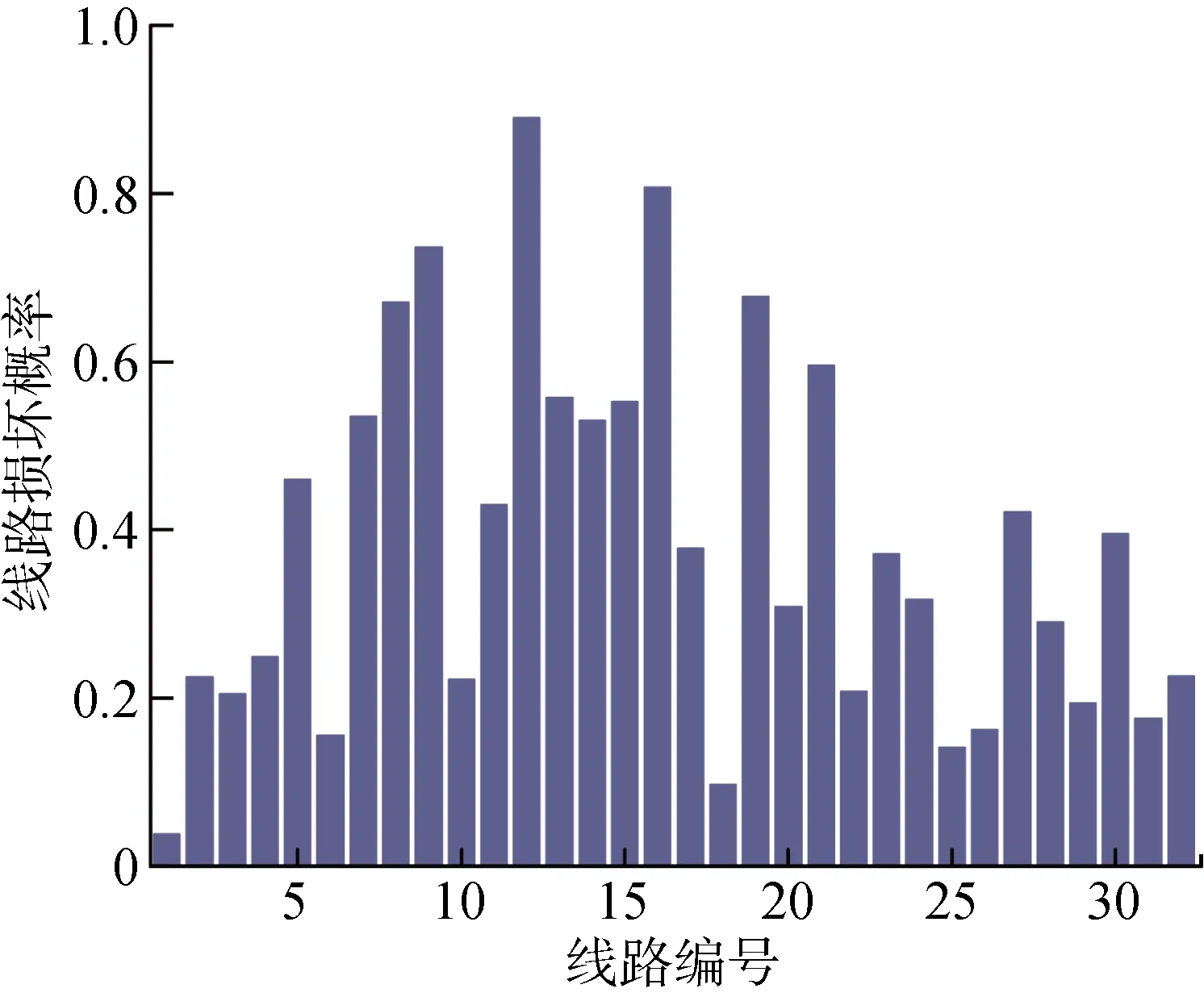
图5 配电网线路故障概率Fig.5 Probability of distribution network line failure

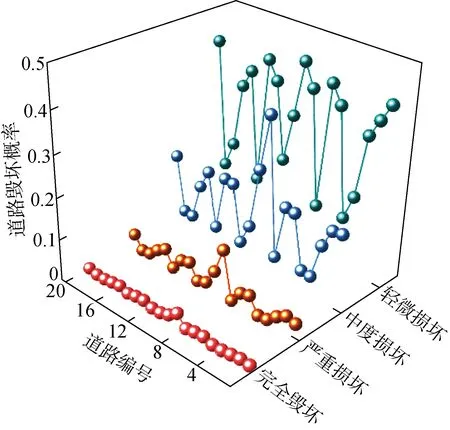
图6 不同程度损伤的道路故障概率Fig.6 Road failure probability with different degrees of damage

由图5可知,各线路所包括的电线杆数量以及位置存在差异,导致各线路故障概率的差异较大.其中,该场景下线路段#7、#8、#9、#12、#13、#14、#15、#16、#19和#21的故障概率较高.由图6可知,大部分道路轻微受损、中度受损的概率较大,所有道路完全毁坏的概率皆小于0.1.其中,由于道路9离震源中心的距离最近,为5 km,所以其受损概率最大,为 0.920 3;严重受损的概率为 0.119 5.在该地震场景下,道路R1、R2、R3、R6、R7、R9、R10、R13、R14、R16、R17和R20的受损概率皆大于50%.

4.2.3故障场景的选取 地震灾害发生后,假设所有故障线路段均可以抢修成功,采用轮盘赌算法,创建配电网、交通网故障场景集.根据文献[17]中的系统信息熵方法筛选发生概率最大的典型场景,其故障场景如附录图4所示;其中故障线路与道路的受损情况如附录表3所示.

假设抢修队于灾害发生4 h后开始进行抢修.抢修队初始位置位于节点1即交通网节点6.该节点配置1个配电网抢修小队、1个道路清理修复小队.抢修过程中地震灾区的天气适合抢修的进行,抢修车的行驶初始速度为40 km/h.基于此研究制定地震灾害后的配电网恢复策略.

4.3 配电网韧性评估分析

为验证地震灾害下配电网韧性评估指标的合理性,考虑是否计及受损交通网进行对比分析.如图7所示,由于受损道路会阻碍配电网抢修队车辆正常行驶,导致系统恢复时间与重要负荷恢复时间较道路完全通畅情况下较长,不考虑道路受损情况会导致韧性评价结果过于乐观,所以本文所提韧性评估指标值低于不考虑受损交通网的韧性指标,两种韧性指标的差异如图中阴影部分所示.分别采用本文提出的韧性指标Rn、文献[32]中的韧性指标Rc和文献[33]中的韧性指标Rr进行评估.如表1所示,韧性指标Rc和Rr在受损交通网下的韧性指标值高于不考虑受损交通网的情况,不符合图7中两种韧性曲线的特征.然而韧性指标Rn值与韧性曲线相对应,表明本文提出的韧性评估指标更为准确.

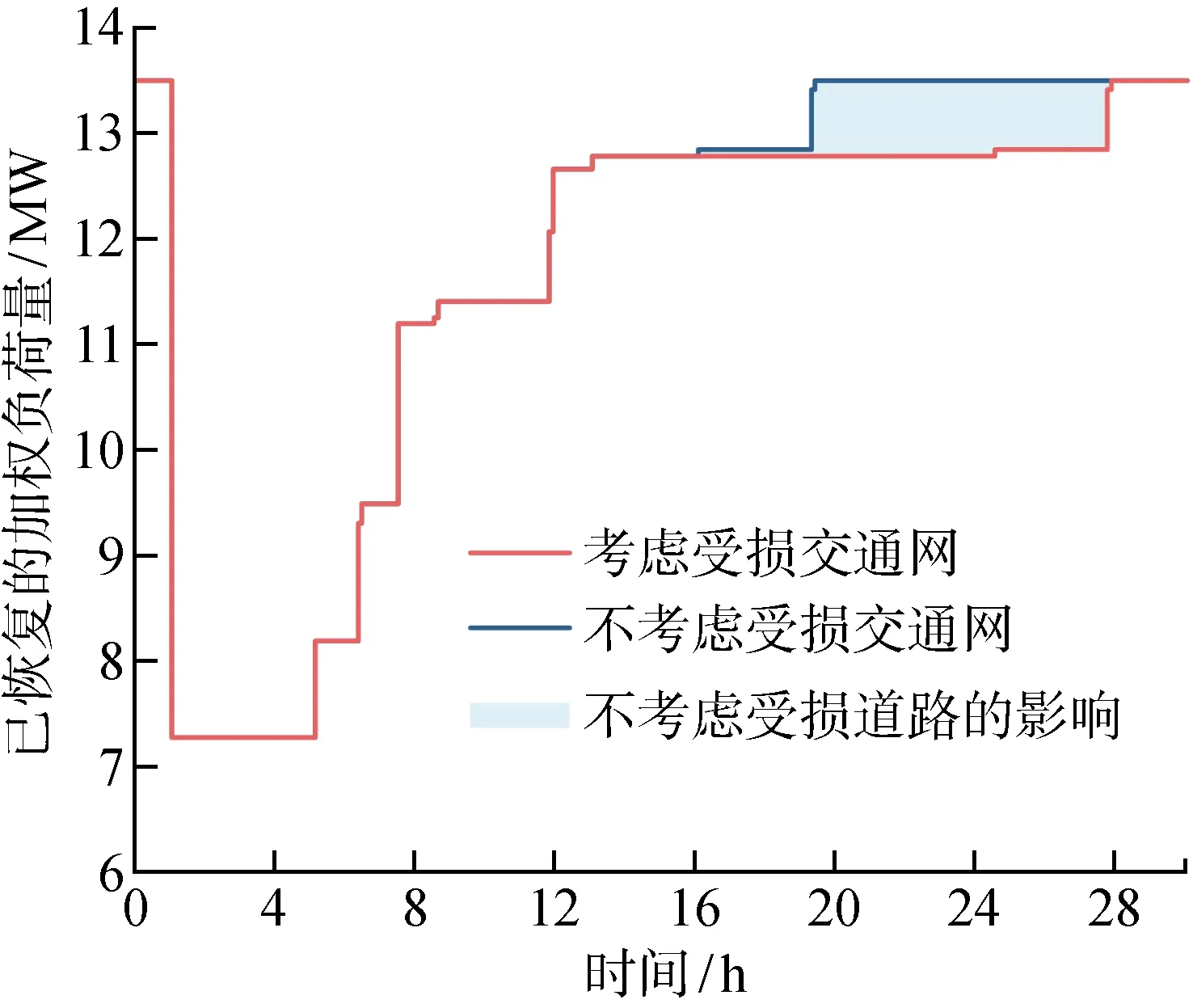
图7 地震灾害下韧性评估指标合理性分析Fig.7 Rationality analysis of resilience evaluation indicators in earthquake disaster

4.4 配电网韧性提升措施分析

为更快恢复灾后配电网重要负荷的正常供电,在抢修资源中增加应急电源车调度用于抢修过程.在配电网节点1,即交通网节点6处配置两辆应急电源车,每辆应急电源车最大输出功率为150 kW,满负荷状态下能持续供电15 h.

在受损的交通网中,考虑两辆应急电源车灵活支援不同故障区域,同时采用双层优化模型确定配电网抢修顺序与交通网修复疏通顺序作为配电网韧性提升优化策略,其抢修及调度顺序均由贪心算法求取,如附录表4所示.考虑应急电源车与道路修复顺序对地震灾害下配电网多故障抢修的影响,在受损交通网中将不同策略中的道路修复顺序及应急电源车调度分别与所提策略进行对比,分析优化策略的优势.

对比策略1:不考虑应急电源车,采用双层优化模型确定配电网抢修顺序与交通网修复疏通顺序恢复故障配电网.

对比策略2:在策略1基础上,不考虑优化交通网修复疏通顺序.交通网修复疏通顺序根据修复难易程度,先修复中度受损道路、后修复严重受损道路.

对比策略3:在策略1基础上,在恢复过程中考虑将两辆应急电源车,并将两辆应急电源车作为一个整体进行调度,为同一个停电区域供电.

对比策略4:在策略3的基础上,考虑两辆应急电源车仅为配电网中失电量最大的停电区域持续供电.

5种优化策略的配电网韧性曲线如图8所示.由于对比策略2未考虑优化受损交通网修复顺序,导致配电网抢修队等待时间过长,故障恢复速度慢,比其他策略长4.5 h,其韧性值较低.本文优化策略与对比策略1、3、4均考虑优化受损交通网修复顺序,虽然故障恢复的时间相同,但由于本文优化策略采用两辆应急电源车的灵活调度,相较于对比策略1、3、4能有效提高地震灾害下配电网韧性.

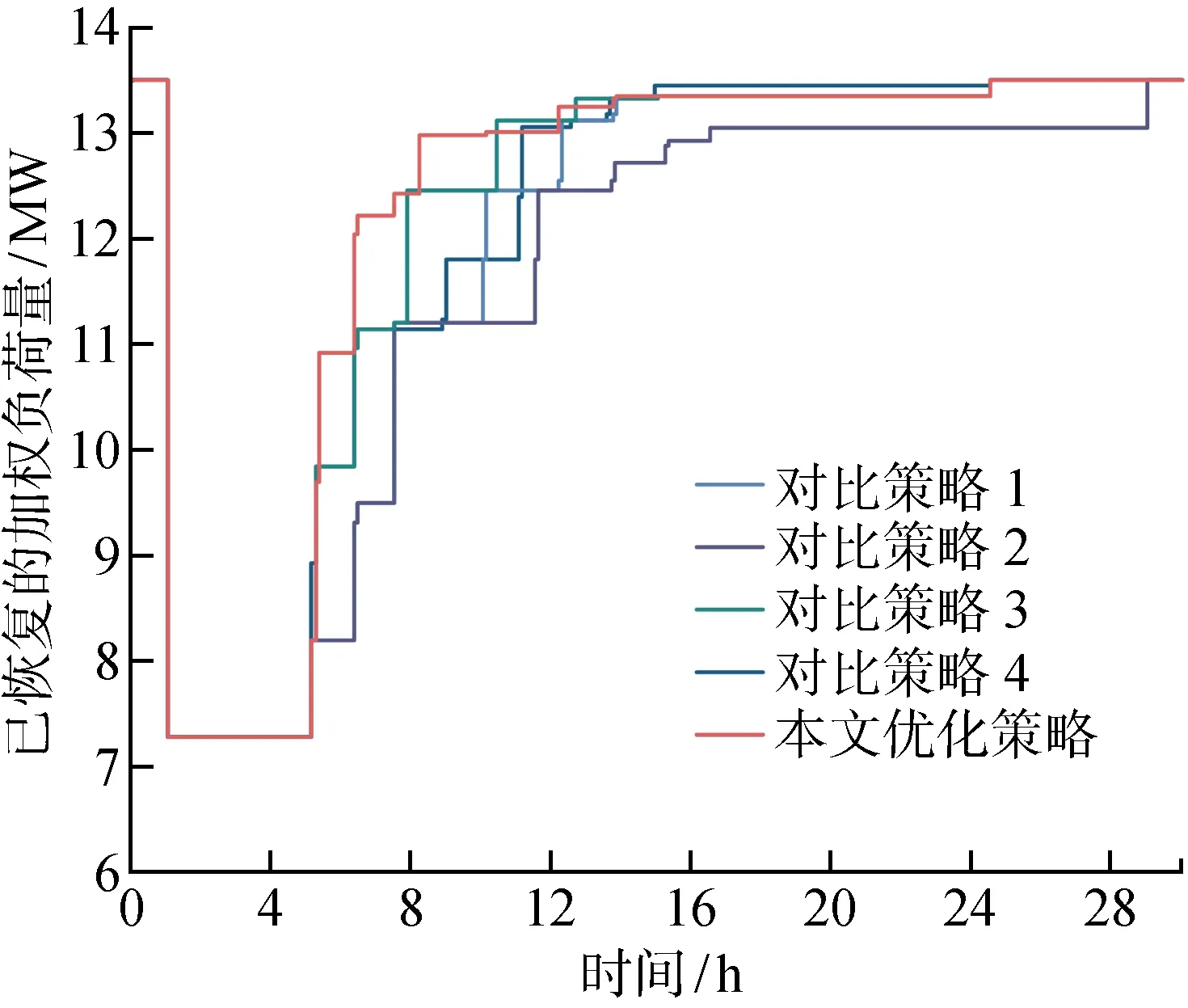
图8 不同策略下韧性曲线图Fig.8 Resilience curves of different strategies

不同策略的韧性指标对比如表2所示.在不考虑应急电源车的情况下,对比策略1优化配电网抢修与交通网修复顺序,其韧性指标值为63.14%,较对比策略2提升9.29%.当应急电源车作为抢修资源进行抢修调度时,对比策略3接入应急电源车后,配电网韧性指标值提升至65.03%.对比策略4采用应急电源车为失电量最大的停电区域持续供电,将其韧性指标值提升至为64.42%,仅较对比策略1提升1.28%.本文优化策略考虑两台应急电源车的灵活调度,其韧性指标值提升效果最佳,较对比策略1提升2.11%;由于应急电源车数量较少,所以相较于对比策略3的韧性值提升不大,但其重要负荷恢复时间远小于对比策略3;同时,重要负荷恢复时长最短,表明本文优化策略更优.

因此,配电网抢修队和交通网修复队的协同恢复能有效提升配电网韧性.在此基础上,加入应急电源车为重要负荷供电能更好地提升配电网韧性.上述结果分析表明,合理的应急电源车调度方案能更大程度提升配电网韧性.

5 结论

考虑地震灾害攻击交通网的影响,提出地震灾害下配电网韧性评估指标以合理描述地震灾害下配电网韧性.构建协同故障线路抢修、道路修复疏通以及应急资源调度的双层优化模型,求解所得的恢复策略可为电力系统调度人员应对地震灾害提供较为完整可行的恢复方案,从而实现地震灾害下配电网韧性的提升.通过算例分析,可以得到以下结论:

(1) 考虑受地震攻击的受损道路对配电网抢修进程有较大影响,本文耦合交通网与配电网,协同故障线路抢修与受损道路修复,更符合现实情况,可为多部门联合应对地震灾害提供理论参考.

(2) 引入配电网抢修队等待道路修复疏通时间,结合配电网功能曲线缺失面积改进韧性评估指标,提出一种适用于地震灾害的韧性评估指标,进一步完善配电网韧性评估理论.

(3) 所提恢复策略可协同配电网故障线路抢修、交通网道路修复以及应急资源调度,有效提高地震灾害下配电网韧性.

综上所述,研究成果可以作为地震灾害下配电网故障抢修问题的基础性和前瞻性工作,为配电网地震灾害下韧性评估提供理论研究基础.由于本文对应急电源车的路径规划仅考虑无损道路和轻微受损道路,未来工作将把中度受损和严重受损道路纳入应急电源车调度路径的规划范围内,结合交通拥堵等交通网特征对配电网韧性评估指标进行改进,进一步研究应急电源车的调度成本及恢复策略的经济性.

附录见本刊网络版(xuebao.sjtu.edu.cn/article/2023/1006-2467-57-09-1165.shtml)