基于改进无源性控制的三相LCL并网逆变器输出导纳重塑方法

2023-09-26张建文

上海交通大学学报 2023年9期

王晗, 张建文, 施刚, 朱淼, 蔡旭

(上海交通大学电力传输与功率变换控制教育部重点实验室,上海 200240)

在能源短缺和全球变暖的影响下,分布式可再生能源发电系统变得越来越重要.一般情况下,可再生能源经由并网变换器将电能馈入电网,但同时不可避免地向电流注入谐波电流.为了有效衰减注入电网的电流谐波,文献[1]中采用LCL滤波器来滤除开关谐波,但LCL滤波器存在固有谐振,可能会破坏系统的稳定性,尤其是在电网阻抗宽范围变化的情况下其稳定性问题尤为突出,这对并网逆变器控制器的设计提出挑战[2].

针对LCL滤波器存在固有谐振的问题,通常采用无源阻尼[3-5]或有源阻尼[6-10]控制技术来消除谐振.其中,无源阻尼方法直接在滤波电路中附加物理电阻,方法简单但会带来额外功率损耗.主动阻尼方法通常采用状态反馈变量构造虚拟电阻来实现,但往往需要额外传感器或复杂的算法.文献[11-12]中发现在控制中:如果LCL谐振频率低于采样频率的1/6,则逆变器侧电流反馈控制不需要额外阻尼即可实现LCL并网变换器的谐振频率控制;而对于电网侧电流反馈控制,LCL谐振频率应高于采样频率的1/6.但上述有源阻尼控制方法的控制效果严重依赖电网阻抗、LCL滤波器参数和采样频率[13].

除了线性控制方法外,考虑到变换器的非线性特性,一些非线性控制方法得到越来越多的研究[14],包括无源性控制(Passivity-Based Control,PBC)[15-16]、预测控制[17-18]和滑模控制[19-20]等.在这些非线性控制方法中,PBC方法以其基于能量耗散和修正方法的高性能和强鲁棒性而受到广泛关注.PBC方法最早由Ortega等[21]在电气系统中提出,该方法采用欧拉(Euler-Lagrange,EL)模型或带耗散的端口控制哈密顿系统方程描述物理系统,通常构造基于李雅普诺夫理论的误差能量函数,并采用阻尼注入设计控制器.文献[22]中采用基于PBC的EL模型,用L滤波器抑制铁路电力系统中的低频振荡.文献[15]中对中性点箝位光伏逆变器实施基于无源性的解耦控制,以避免参数扰动,但未考虑电网阻抗.为了减小稳态误差,提高系统鲁棒性,文献[16]中提出基于PBC的LCL滤波并网逆变器阻尼增益的设计方法,但未考虑精确的控制延迟.在某些情况下,并网逆变器通常在分布式发电系统中的公共耦合点(Point of Common Coupling,PCC)与电网连接在一起;在长电缆或更复杂的电网中,等效电网阻抗可能是电容性的,从而引发并网变换器的不稳定.针对基于LCL并网电压源逆变器(LCL Voltage Source Inverter,LCL-VSI)系统,文献[23]中指出传统PBC方法较少考虑电网阻抗的电容效应以及精确的数字控制延迟,导致数字控制系统容易出现交互共振的问题[24-25].因此,复杂电网阻抗情况下PBC控制器的设计非常重要.虽然PBC被定义为基于能量耗散的非线性控制,但控制律可以用线性控制块来实现,因此PBC结合了前馈控制、负反馈控制和解耦控制.为了克服电网阻抗的不确定性,基于阻抗的方法被用于评估并联VSI系统的稳定性和动态相互作用[26-27].文献[28]中分析了采用传统比例(Proportion Integral,PI)或谐振控制器的单回路网侧电流控制和变流器侧电流控制的无源特性,但很难保证所有区域的无源性.

鉴于此,建立三相LCL并网逆变器的EL模型,推导基于逆变器侧电流控制的传统PBC控制律,建立逆变器的输出导纳模型.基于频域无源性理论,分析延迟效应对逆变器输出导纳的影响及其非无源区域,采用电容电流前馈来扩展无源区域,实现奈奎斯特频率范围内输出导纳的无源性.最后,利用仿真和实验验证了所提方法的有效性.

1 三相LCL并网逆变器的传统PBC控制

1.1 系统建模

图1为三相LCL并网逆变器的系统示意框图.图中:LCL滤波器包括变换器侧电感L1、滤波电容C和网侧电感L2;R1和R2分别为L1和L2的等效寄生电阻;i1和ui分别为脉宽调制逆变器的输出电流和电压;uc和ic分别为电容器的电压和电流;udc和Cdc分别为直流电压、电容;i2为注入电网的电流;upcc为PCC点电压;Zg为电网的阻抗,由电网等效电感Lg和电网等效电容Cg组成.

三相LCL并网逆变器在同步旋转dq坐标系中的数学模型可由变换器侧电压方程、LCL滤波器电容电压方程和变换器侧电流方程等3个方程表示,其中变换器侧电压方程为

(1)

式中:t为时间;ω为电网角频率;变量的下标d和q分别对应物理变量在dq旋转坐标系下的d轴分量和q轴分量.

LCL滤波器电容电压方程为

(2)

变换器侧电流方程为

(3)

EL方法是非线性PBC理论的重要组成部分,常被用来描述系统模型.由于逆变器侧电流是受控的,滤波电容器和滤波电感可以与电网阻抗一起考虑,所以只需设计逆变器侧电流变量的EL模型即可.因此式(1)可写为EL模型的形式,其表达式为

(4)

式中:

式(4)被视为状态方程.M和R为正定对角矩阵,其中R代表系统的内部能量耗散特性;J为描述d轴和q轴电流分量之间内部耦合结构的斜对称矩阵;u为控制输入矩阵,代表系统和外部能量输入.

1.2 传统PBC控制律与阻尼注入

根据无源性理论[15,17],假设某系统的输入和输出变量分别为u和y,如果存在正定函数Q(x)和非负存储函数V(x)满足如下不等式,则系统被认为是严格无源的.

(5)

式中:uTy为外部能量的注入速率.式(5)表示系统增加的能量之和总是小于外部注入能量之和.

对于LCL并网逆变器,定义正定函数V(x)表示系统存储的能量,其表达式为

V(x)=xTMx

(6)

对于式(6),取系统能量函数式(5)的时间导数并结合式(4)可得:

xTu-xTJx-xTRx

(7)

根据无源性理论,式(7)中描述的对象是严格无源的,可以采用传统的PBC来设计控制器.考虑逆变器侧电流控制,则系统的状态变量可定义为

(8)

定义电流的误差向量为xe=x*-x,根据式(4)得到系统的误差EL方程,即

(9)

对式(9)进行重新整理,可得:

(10)

对于式(10),如果误差xe等于0,即可实现期望的控制目标,使系统在期望的工作点稳定运行.为了改进系统的动态速度,可在式(10)中添加正阻尼矩阵Rd,使加速误差达到0.定义注入的阻尼项为

(11)

式中:r1为阻尼系数.

增加阻尼项后,系统新的耗散项可描述如下:

(12)

将式(12)引入式(10),则注入阻尼后误差方程可改写为

Rx*+Rdxe-u=H

(13)

将H设为Jxe可消除系统的耦合项.则由式(13)可得出系统的控制律如下:

(14)

根据前述分析,基于PBC方法的三相并网逆变器的频域dq控制率框图如图2所示.图中:L1e和R1e为控制器中设计的LCL滤波器参数;s为拉普拉斯算子.在具体实现过程中,可用PI控制器代替r1来减小稳态误差.

图2 基于传统PBC的并网逆变器控制率Fig.2 Control structure for three-phase grid-connected inverter based on PBC

2 带PBC的LCL并网逆变器阻抗模型及稳定性分析

2.1 带PBC的LCL并网逆变器

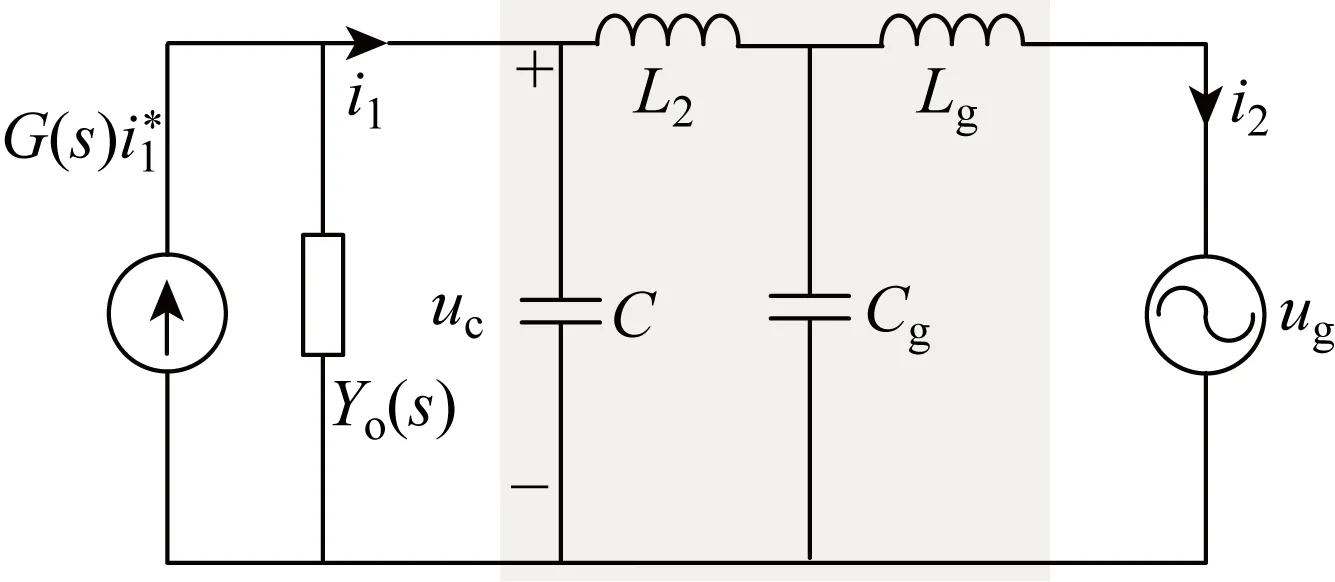
图3 LCL并网逆变器的诺顿等效模型Fig.3 Norton equivalent model of LCL grid-connected inverter

(15)

式中:G(s)决定LCL并网逆变器变换器侧电流控制的动态响应和稳态误差.

将滤波电容C、网侧电感L2以及电网阻抗Zg视为并网变换器的外部阻抗,定义Ygt(s)为逆变器侧总的外部电网导纳,如图3中阴影部分,其表达式可表示如下:

(16)

结合式(15)和(16),可推导出并网逆变器变换器侧电流与电网电压的电流响应为

(17)

由式(17)可知,并网逆变器系统的动态响应和外部干扰稳定性与传递函数Yo(s)/Ygt(s)有关,因此,Yo(s)和Ygt(s)均应为无源,才能保证并网逆变器和电网互联系统的稳定性.但由于Ygt(s)由电阻、电感和电容组成,显然是一个无源网络,所以PBC控制并网逆变器的输出阻抗Yo(s)应该无源才能保持系统稳定.

由于需要考虑系统采样延迟和控制延迟,式(14)考虑延迟后的并网逆变器控制律可表示为

u*=uGd(s)

(18)

式中:Gd(s)=e-1.5Tss为计算和调制延迟,其中Ts=1/fs为采样周期,fs为采样频率.

根据图2可将PBC控制LCL并网逆变器的控制律写为

(19)

式中:ω=2πf,E=sL1e+R1e+r1.

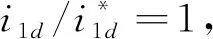
Gd(s)=

(20)

LCL并网逆变器的输出导纳可表示为

Yo(s)=

(21)

2.2 基于无源性理论的LCL并网逆变器系统稳定性分析

根据无源性理论,基于PBC的LCL并网逆变器稳定需满足如下两个条件:①闭环传递函数G(s)应该没有右边平面极点;②逆变器的输出导纳Yo(jω)应具有非负实部,或Yo(jω)的相位φ(jω)在 [-90°,90°]范围内,即ReYo(jw)≥0⟺argYo(jω)∈[-90°,90°], ∀ω>0.

系统参数分别为udc=350 V;L1=1.2 mH;L2=1.2 mH;R1=0.1 Ω;R1=0.2 Ω;C=6 μF;fs=10 kHz;开关频率fsw=10 kHz;Ug=110 V;电网频率fo=50 Hz.根据式(21),图4给出阻尼系数r1变化下LCL并网逆变器输出导纳Yo(s)的实部和频率f的三维图.要使逆变器系统稳定不受外部环境影响,则系统应该无源,即并网逆变器的输出导纳Yo(s)的实部应该大于0.

图4 不同阻尼系数r1下并网逆变器输出导纳Yo(s)的实部随频率的变化Fig.4 Real part of the output admittance Yo(s) of grid-connected inverter versus frequency at different r1 values

由图4可以看出,PBC控制下并网逆变器的等效输出导纳Yo(s)存在负电阻会导致系统不稳定.r1越小,系统的无源区域越大,系统稳定性越好,但不能满足奈奎斯特频域内无源;当r1>14时,系统在全频域非无源,无论Ygt值是多少,逆变器都会和电网存在交互谐振.

图5给出r1变化下G(s)的阶跃响应y(t)波形.由图可见,随着r1增大,G(s)的动态响应和带宽越好.图5可用以帮助选择r1,可根据超调性能和设定时间令r1在3～6取值.因此,r1应在4～9取值以使系统获得更好的稳定裕度.同时,考虑G(s)的稳定性和系统动态响应,r1取值为6.

图5 不同阻尼系数r1下G(s)的阶跃响应Fig.5 Step responses of G(s) at different r1 values

3 基于电容电流前馈的阻尼增强方法

为了扩大系统的无源性区域,需要研究系统阻尼的增强方法.为了重塑并网逆变器的输出导纳,可考虑引入电容电流前馈,图6为基于电容电流前馈的阻尼增强控制框图.图中,K(s)为有源阻尼环节,Δu=K(s)ic为电容电流前馈.

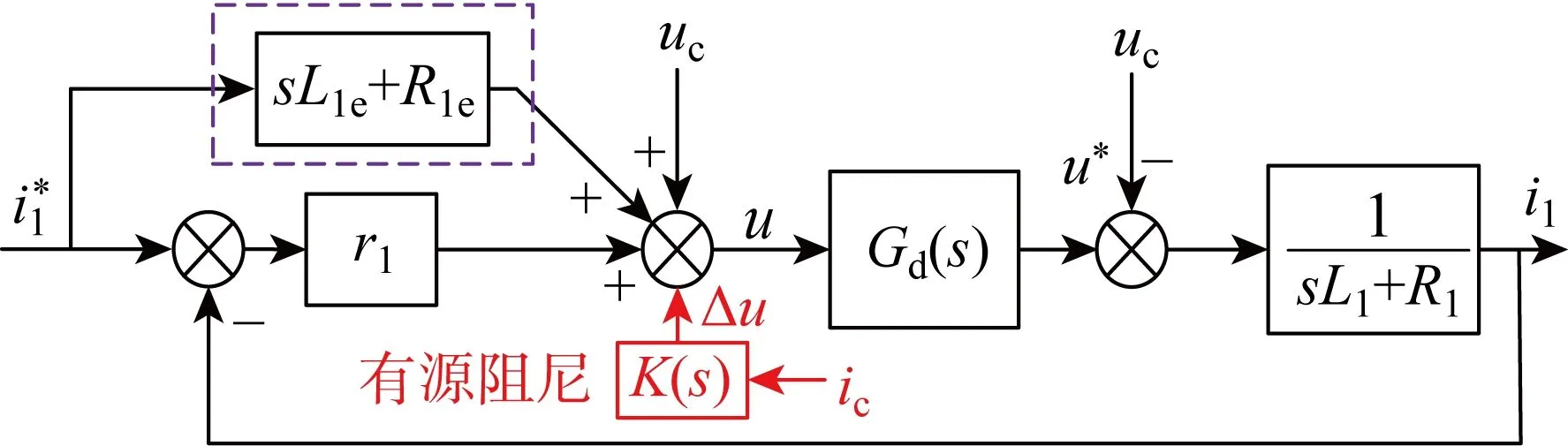
图6 基于电容电流前馈的阻尼增强控制框图Fig.6 Block diagram of damping enhancement control based on capacitive current feedforward

取K(s)为比例环节,即K(s)=kd,kd为电容电流前馈系数.考虑到滤波器电容电流ic=sCuc,可得Δu=K(s)ic=kdsCuc,则引入电容电流前馈后PBC控制并网逆变器的控制律可表示为

(22)

考虑延时后由式(22)可得引入电容电流前馈后PBC控制并网逆变器的输出导纳为

Yo(s)=

(23)

不同电容电流前馈系数kd下并网逆变器输出导纳和系统等效网络导纳Ygt(s)的伯德图如图7所示.图中:Y(ω)为幅值;φ(ω)为相位.由图7可知,加入比例前馈后,并网逆变器在高频段的非无源区域变窄,可提高系统的稳定性,前馈系数越高抑制效果越好,但非无源性区域不能完全被消除;此外,如果前馈系数大到一定数值(如kd=21),则会在低频和中频引入新的非无源性区域.

图7 不同比例前馈系数的输出导纳Yo(s)和等效网络导纳Ygt(s)的伯德图Fig.7 Bode wave of Yo(s) at different proportional feedback coefficients and Ygt (s) values

为了使并网逆变器输出导纳在奈奎斯特频率无源,在基于PBC的电容电流前馈回路中加入高通滤波器(High Pass Filter, HPF)替代比例前馈,其表达式为

(24)

式中:ωh为高通滤波器的截止角频率.

将式(23)中的比例环节用式(24)替代后,不同电容电流前馈系数kd下并网逆变器输出导纳Yo(s)和等效导纳Ygt(s)的伯德图如图8所示.由图8可知,高通滤波器替代比例环节对Yo(s)的低频段特性几乎没有影响,且可有效扩大系统在奈奎斯特频率附近或更高频率段的无源性区域.选择高频滤波器K(s)的截止频率为 1 600 Hz,电容电流前馈系数kd为7,可在奈奎斯特频率范围内,保证改进PBC控制并网逆变器并弱电网的稳定性.Yo(s)的幅值在低频范围内足够小,说明改进的PBC控制使逆变器具有较强的电网谐波电压抑制能力.

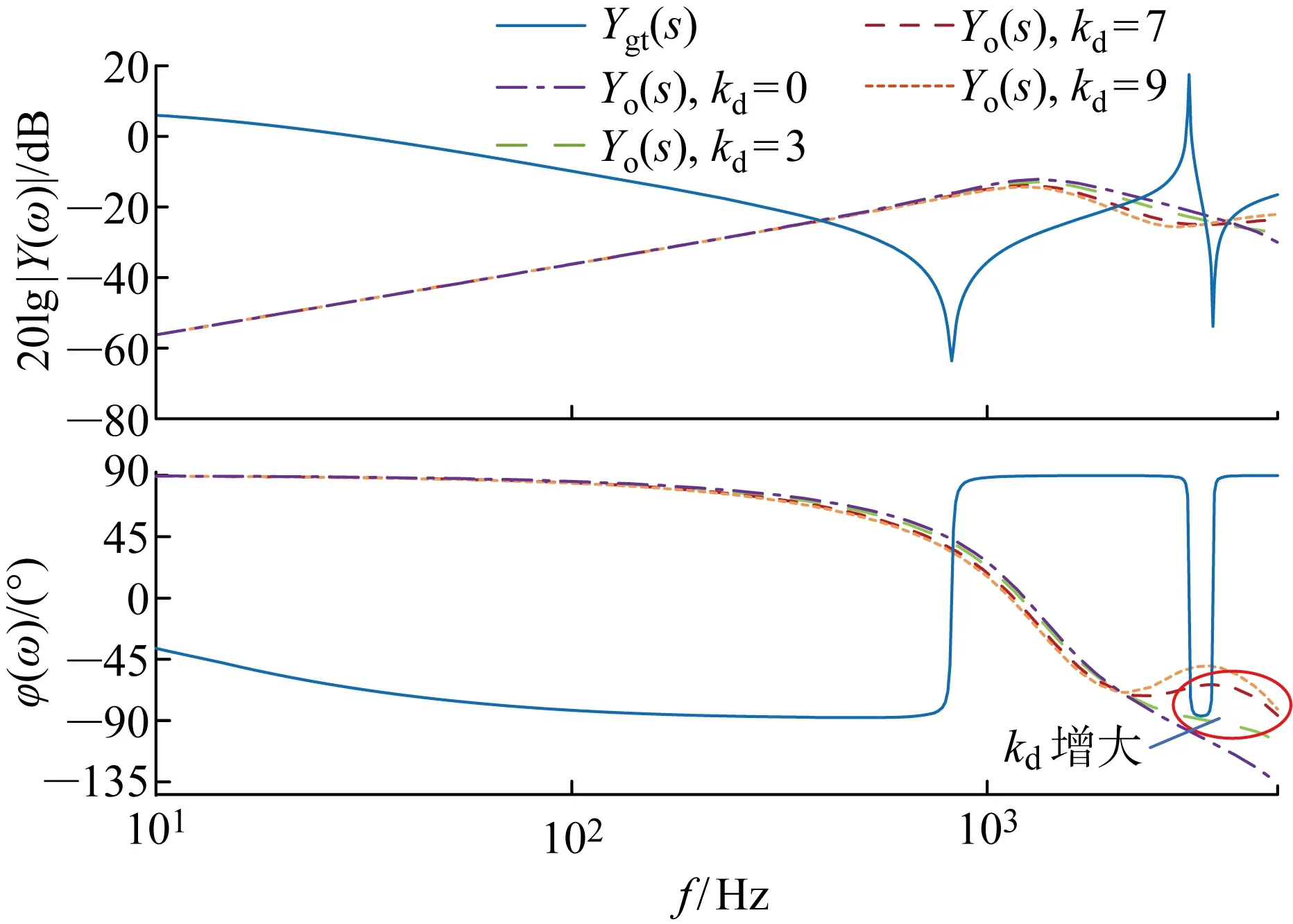
图8 不同HPF前馈系数的输出导纳Yo(s)和等效网络导纳Ygt(s)的伯德图Fig.8 Bode wave of Yo(s) at different HPF feedback coefficients and Ygt(s) values

4 仿真和实验验证

4.1 仿真结果

为了验证本文所述控制方法的有效性,开展基于MATLAB/Simulink的PBC三相LCL并网逆变器系统的仿真验证.仿真中并网逆变器的电容电流前馈系数kd=7,阻尼系数r1=6,其他参数如2.2节所示,仿真波形如图9～图12所示.

图9 强电网下不同电容电流前馈控制的并网电流仿真波形(Lg=0,Cg=0)Fig.9 Simulation waves of grid currents of different capacitor current feedback methods (Lg=0, Cg=0)

图9给出在强电网中采用不同电容电流前馈控制策略时,PBC控制LCL并网逆变器并网电流的波形.仿真设置如下:在0.12 s前,采用HPF电容电流前馈控制;在0.12 s时,采用比例电容电流前馈控制;0.16 s时,不采用任何有源阻尼策略.由波形可见,强电网下当采用有源阻尼控制策略时并网电流均是稳定的;当不采用任何有源阻尼策略时,并网电流出现振荡,系统存在失稳问题.

图10为当Lg=0且Cg=0时,无电容电流前馈时Yo(s)和Ygt(s)的伯德图.由图可见,在交互点处Yo(s)和Ygt(s)的相位差大于180°,可知PBC控制的三相LCL并网逆变器可能会因延迟的影响而不稳定,应采用阻尼增强方法.

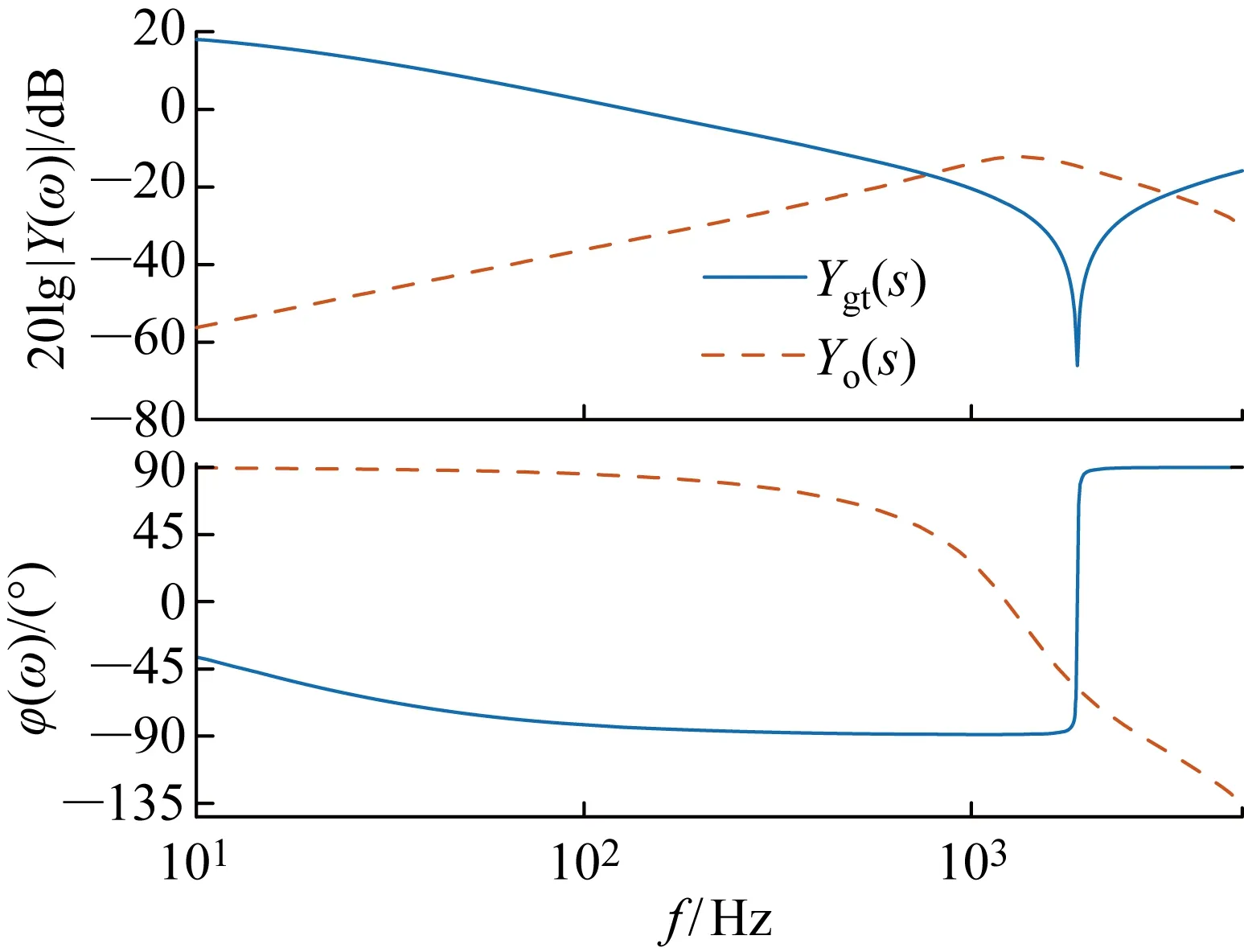
图10 无电容电流前馈下Yo(s)和Ygt(s)的伯德图(Lg=0, Cg=0)Fig.10 Bode waves of Yo(s) and Ygt(s) without capacitor feedforward at Lg=0 and Cg=0

当并网逆变器经长电缆接入电网时,电网等效阻抗中的C不可忽略,当Lg=3.6 mH、Cg=2 μF时,采用不同电容电流前馈方法的三相LCL并网逆变器的并网电流如图11所示.由图可知,在容性电网下,在奈奎斯特频率之前系统存在非无源区域,且不能用kd前馈控制进行完全补偿;在0.12 s时,当切换到提出的HPF前馈控制后,并网谐振电流得到有效抑制,并网逆变器逐渐趋向稳定.

图11 考虑线路电容效应下不同电容电流前馈控制的并网电流仿真波形(Lg=3.6 mH,Cg=2 μF)Fig.11 Simulation waves of grid currents of different capacitor current feedforward methods (Lg=3.6 mH, Cg=2 μF)

为验证多提改进有源阻尼策略对电网谐波的抑制能力,容性电网下0.12 s时往电网中注入3、5、7、11次谐波,谐波分量分别为5%、5%、5%、1.5%,结果如图12所示.从图中可以看出,在0.12 s后电网电压发生了畸变,但是入网电流依然保持正弦.

图12 电网含背景谐波的并网电流仿真波形(Lg=3.6 mH,Cg=2 μF)Fig.12 Simulation waves of grid currents of proposed control method in distorted grid (Lg=3.6 mH, Cg=2 μF)

4.2 实验结果

为了进一步验证提出控制方法的有效性,在实验室对一台3 kW三相LCL并网逆变器开展实验研究.其中,控制器采用dSPACE DS1202,直流电源采用Chroma 62150H-600S,电网由Chroma 61830三相电网模拟器产生.系统参数与仿真实验相同,HPF前馈系数kd取7,注入阻尼r1取6.实验波形如图13～16所示.图中:下标a、b分别表示a、b相.

图13 提出控制策略下LCL并网逆变器的稳态实验波形(Lg=3.6 mH,Cg=3 μF)Fig.13 Experimental waveforms of proposed control method (Lg=3.6 mH and Cg=3 μF)

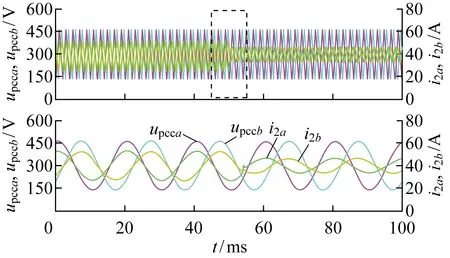
图14 提出控制策略下LCL并网逆变器的暂态实验波形(Lg=3.6 mH,Cg=3 μF)Fig.14 Dynamic experimental waveforms of proposed control method (Lg=3.6 mH and Cg=3 μF)

当Lg=3.6 mH和Cg=3 μF时,提出的控制策略下LCL并网逆变器的电压和电流波形稳态实验波形如图13所示.由图可知,并网电流正弦且与PCC电压同步,这使电流注入性能与电容电网中的分析一致,验证了所述控制策略可实现并网逆变器的稳定运行.

当参考电流从12.8 A跌落至6.4 A时,所提控制策略下LCL并网逆变器的暂态并网电流实验波形如图15所示.由图可知,在容性电网中,采用所述控制策略可实现并网逆变器的暂态稳定运行,且系统具有较快的暂态特性.

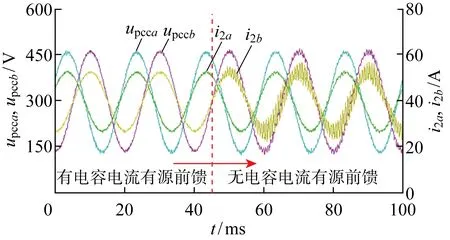
图15 提出控制策略下HPF前馈被禁止时LCL并网逆变器的实验波形(Lg=3.6 mH, Cg=3 μF)Fig.15 Experimental waveforms of proposed control method at disabled HPF feedback (Lg=3.6 mH, Cg=3 μF)

图15给出Lg=3.6 mH和Cg=3 μF时所述控制策略突然禁止时LCL并网逆变器的实验波形.由图可见,当所述HPF前馈控制方法使能时,LCL并网逆变器的并网点电流和电压均保持正弦,系统运行稳定;当不使用HPF前馈控制方法时,LCL并网逆变器的并网电流和电压出现振荡发散现象,进而验证了所述控制方法的有效性.

图16为提出控制策略下电网中存在3、5、7次谐波电压的实验波形.由图可见,虽然电网压发生畸变,但入网电流波形质量较好,验证了所述控制方法有较好的谐波抑制能力和抗扰性.

图16 电网含背景谐波电压时提出控制策略下的实验波形(Lg=3.6 mH, Cg=3 μF)Fig.16 Experimental waveforms of proposed control method at grid background harmonic voltage (Lg=3.6 mH, Cg=3 μF)