钻井立管下放安装过程中涡激振动响应实验研究*

2023-09-26李效民柳润波顾洪禄李福恒郭海燕

中国海洋大学学报（自然科学版） 2023年10期

李效民, 柳润波, 顾洪禄, 李福恒, 郭海燕

(中国海洋大学工程学院, 山东青岛 266100)

海洋立管是连接海洋平台和海底设备的纽带,是深水油气资源开发的核心构件。深海钻井立管力学性能特殊,是薄弱易损构件之一。在安装过程中立管底部处于悬空状态,水下长度随着立管下放逐渐变长,且下端没有任何约束限制。此时,相比于已经安装完成的立管,悬挂式立管更脆弱、不稳定,下放过程中产生的涡激振动也会加速立管的疲劳破坏,这导致其在复杂海洋环境下的安装窗口时间大大缩短,因此必须保证立管在安装时的整体稳定性。如何在复杂海况下安全、快速地安装钻井立管已经成为海洋立管研究中的关键问题之一。

当前关于立管安装过程的研究主要集中在数值模拟方法上。林秀娟等[1]开发了一个用于深海采油树下放安装的分析模型,可以分析立管的动态响应。龚铭煊等[2]考虑不同边界条件建立了悬挂立管力学模型,使用有限元方法对下放到不同水深时立管的力学特性进行了研究。Hu等[3]基于有限差分法将立管近似离散成多个刚性段,建立了不同边界条件、不同水深下的动力模型,分析了安装下放时不同长度立管的动态响应。Wang等[4-6]采用变分法分析了立管安装过程中的应力、变形和振动特性,并基于立管安装时的力学行为,给出了立管安装时的安全操作窗口。Wang等[7]把水下集束管汇的安装分成3个阶段,并用OrcaFlex软件对其安装过程进行了建模分析。Liu等[8]建立了一个有限元模型,用于研究紧急疏散条件下深水钻井平台立管系统的动态行为。Tian等[9]通过有限差分法建立了一个双立管模型,将生产立管和安装钻井立管串联布置,考虑生产立管干扰效应,研究了水深、立管壁厚和水下防喷器质量对钻井立管安装的影响。Liu等[10]建立了一个考虑复杂边界条件的数学模型,将立管简化为弹性杆和块体的组合,研究了深水钻井立管在提升工况下的轴向振动。

而当前相关的实验研究还仅限于软、硬悬挂立管以及相关模型的动力响应,并未考虑立管的下放过程。Gao等[11]对均匀流中自由悬挂圆柱体的轨迹和流态进行了实验研究,探究了外部流速对圆柱体轨迹响应和尾流模式的影响。Wang等[12]对深水井中自由悬挂式立管在船舶运动下的动力响应进行了实验研究,研究表明船舶运动引起的涡激振动导致立管受到的阻力显著增大。Mao等[13]基于应变仪测试技术对悬挂式疏散立管进行了模型实验,考虑轴向拉力和立管下部组件(Lower marine risers package, LMRP)质量等因素的影响,采用有限元特征值法分析了悬挂立管的固有频率和振型。Jung等[14]对自由悬挂立管在静水中的受迫振动进行了数值和实验研究。Franzini等[15]研究了倾斜圆柱体在水流中的动力响应,得出了一定雷诺数范围内倾斜圆柱体的涡激振动新测量值。

综上所述,国内、外学者大多是对下放到特定阶段的立管进行研究,并未对立管安装下放的连续过程进行实验研究,也没有深入了解安装下放时立管的涡激振动特性,对带有重型LMRP的悬挂式立管在安装下放过程中变形机制和振动特性的了解还远远不够。为进一步探究钻井立管下放时的动力响应,本文基于光纤光栅技术设计了悬挂立管模型的安装下放实验,通过有限元法分析了模型的固有频率和振型函数,再通过模态叠加法重构立管位移,研究并分析了底部悬挂不同质量的LMRP对立管安装下放过程中动力响应的影响。

1 实验描述

1.1 实验装置

实验在中国海洋大学山东省海洋工程重点实验室波流水槽进行,水槽长60 m、宽3 m、深1.5 m。在实验过程中,水流发生器模拟了流速为0.4 m/s的均匀水流,并在实验支架前2 m处安装了多普勒测速仪,用来实时监测立管下放过程中的水流速度,实验装置如图1所示。在开始下放前,立管完全露在水面以上,立管模型上端通过万向节连接到可以上下滑动的支架顶板上,立管底部是自由端,通过万向节悬挂着不同质量的柱型铁块,用于模拟LMRP重物,铁块底部紧贴水面,如图2所示。实验支架和实验槽之间通过夹紧装置固定,防止在水流作用下支架与模型之间的耦合振动。

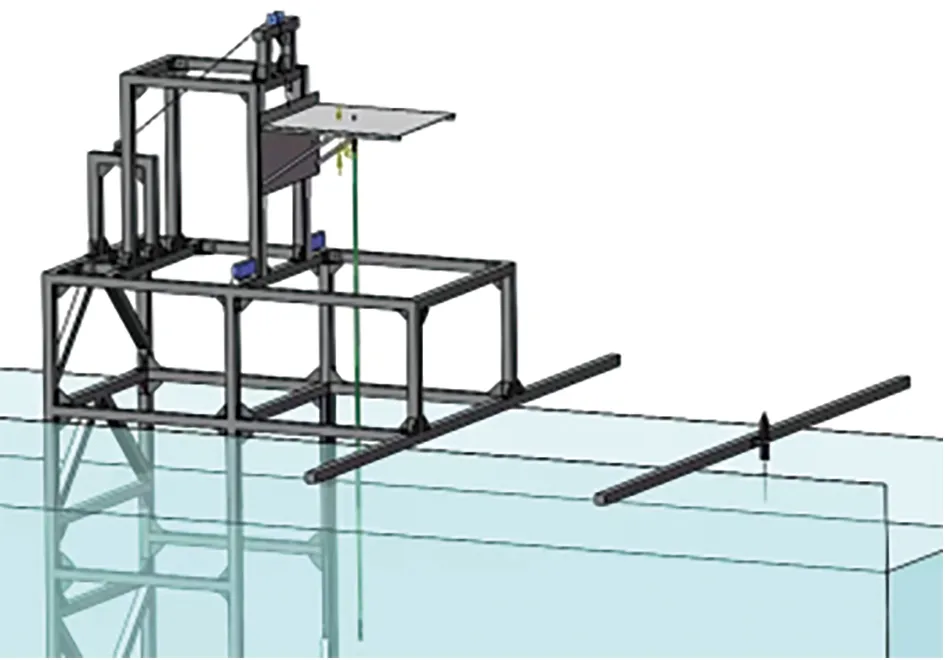
图1 实验装置图

图2 立管模型图

等到多普勒测速仪显示水流速度稳定时立管开始下放。实验通过绞盘来控制绞线实现立管的匀速下放,开始下放的同时采集应变传感器数据,待立管底部触底时停止采集。由于支架上顶板的重力远大于滑轨的摩擦力,故绞盘绞线的释放速度可以看作是顶板的下放速度。定制绞盘的小齿轮每转动10齿,支架上顶板就会下降0.03 m。水槽的水深控制在1.2 m,实验保持每秒一齿的下放速度,400 s后立管下放到水槽底部,实验工程设置如表1所示。

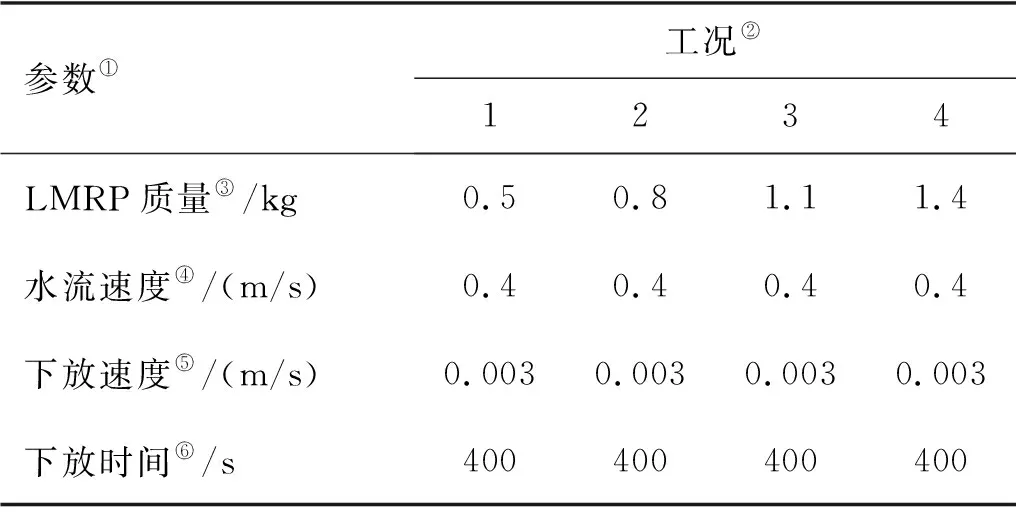
表1 工况设置

1.2 立管模型设计

在测试了各种类型管道的机械性能并考虑了刚度和模态要求之后,选择透明有机玻璃管作为立管模型材料。立管模型主要参数如表2所示,横截面和应变传感器布置如图3所示。立管模型由有机玻璃管和紧贴在管上的光纤光栅应变传感器组成,沿立管长度均匀布置6个应变测试点,其中1号测试点的一端为立管模型顶部,6号测试点的一端为立管模型底部。每个测试点(绕管一圈)布置4个应变传感器,2个在横流(Cross-line, CF)方向,2个在顺流(In-line, IL)方向,测试点间距为0.30 m,立管顶端和底端留有0.25 m的边距,应变仪的采样频率为1 000 Hz。

表2 立管模型的主要参数

图3 应变传感器布置示意图

2 位移重构

2.1 模态叠加法

实验使用光纤光栅应变传感器测量立管的应变响应。根据Li等[16]的数据处理方法,VIV在CF方向和IL方向引起的弯曲应变可以写成:

(1)

(2)

式中:εVIV-IL和εVIV-CF分别是涡激振动在IL和CF方向上引起的平均应变;εCF1、εCF2、εIL1和εIL2分别表示在位置CF1、CF2、IL1、IL2的原始应变采样数据。

为了消除环境噪声对测量应变的影响,本文使用带通滤波对实测应变进行滤波,滤波范围为0.5～19 Hz。基于应变数据,根据模态叠加法可以获得立管的VIV位移响应。只要沿立管布置足够数量的传感器,且位置合理,就可以通过模态叠加法得到任意位置的位移响应。根据模态叠加法,立管位移响应y为不同模态函数的线性叠加:

(3)

式中:ωn(t)是模态权重;φn(z)是模态函数;z是沿立管轴向位置,单位是m;t是立管下放时间,单位是s。

对于本文中的立管模型,弯曲应变ε和曲率κ之间的关系可以表示为:

κ(z,t)=ε(z,t)/R。

(4)

式中R是立管模型的外半径。

根据几何关系,曲率值可近似为位移相对于空间变量的二阶导数:

(5)

通过将式(5)代入式(4),可以得到式(6):

(6)

式中N是立管模型振动涉及的最高振型数。

2.2 频率及振型分析

使用有限元法对立管模型的前6阶固有频率和振型进行计算,计算结果如表3、4和图4所示。由于几何对称性,立管模型在IL和CF这两个方向上的固有频率和模态相同。表3展示了没有悬挂重物和底部悬挂不同重物时立管模型的前六阶频率。悬挂重物的立管模型频率要明显低于普通立管模型频率,且重物质量越大,频率降低的幅度越小。表4展示了考虑水流附加质量影响的悬挂0.8 kg重物立管模型在下放过程中的频率变化,随着立管的下放,附加质量逐渐增大导致了立管的振动频率逐渐变小。图4(a)—(f)展示了悬挂立管模型和普通悬臂模型的前六阶振动模式。悬挂重物不会影响立管振型的振幅,只会影响立管振型底部的位移,立管底部悬挂的重物相当于给立管增加了一个约束,限制了立管底部的位移,变成了类似于简支梁的振型。

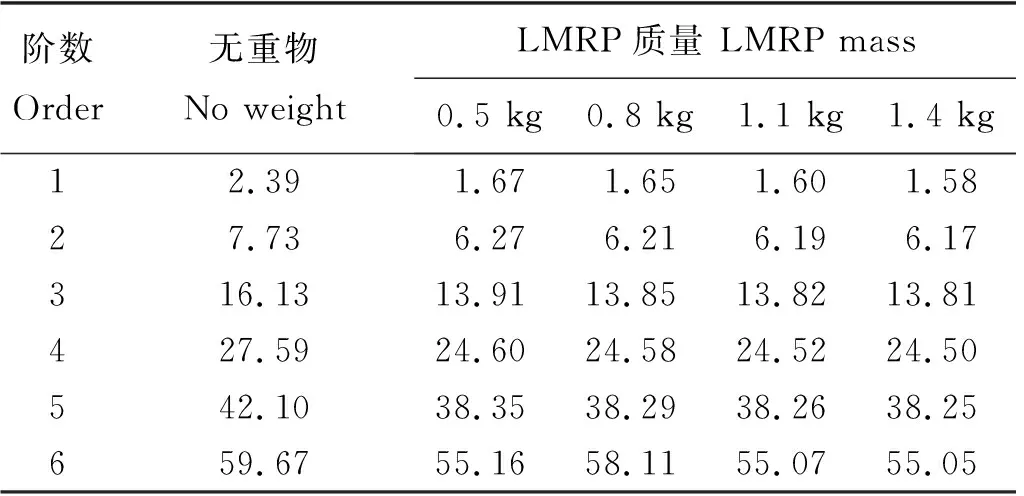
表3 立管模型的前六阶固有频率

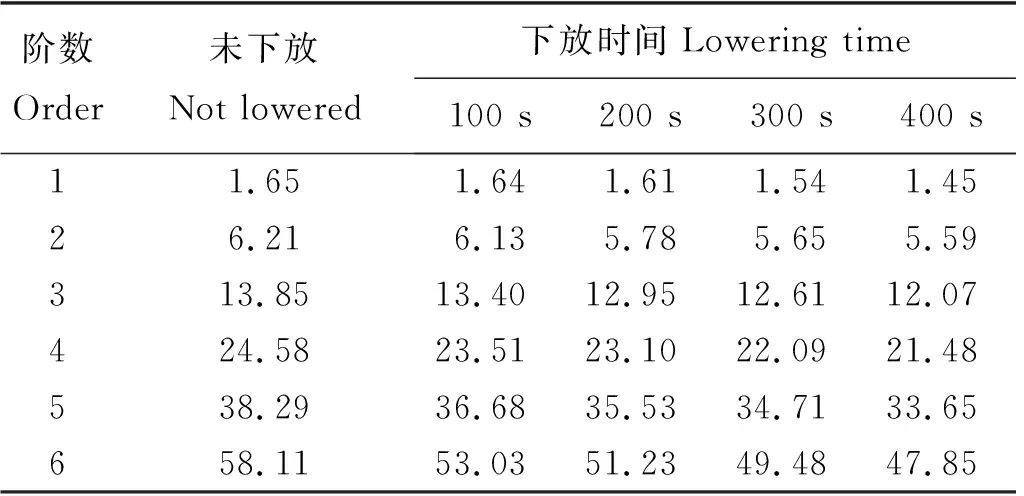
表4 悬挂0.8 kg重物立管模型下放过程中的频率变化

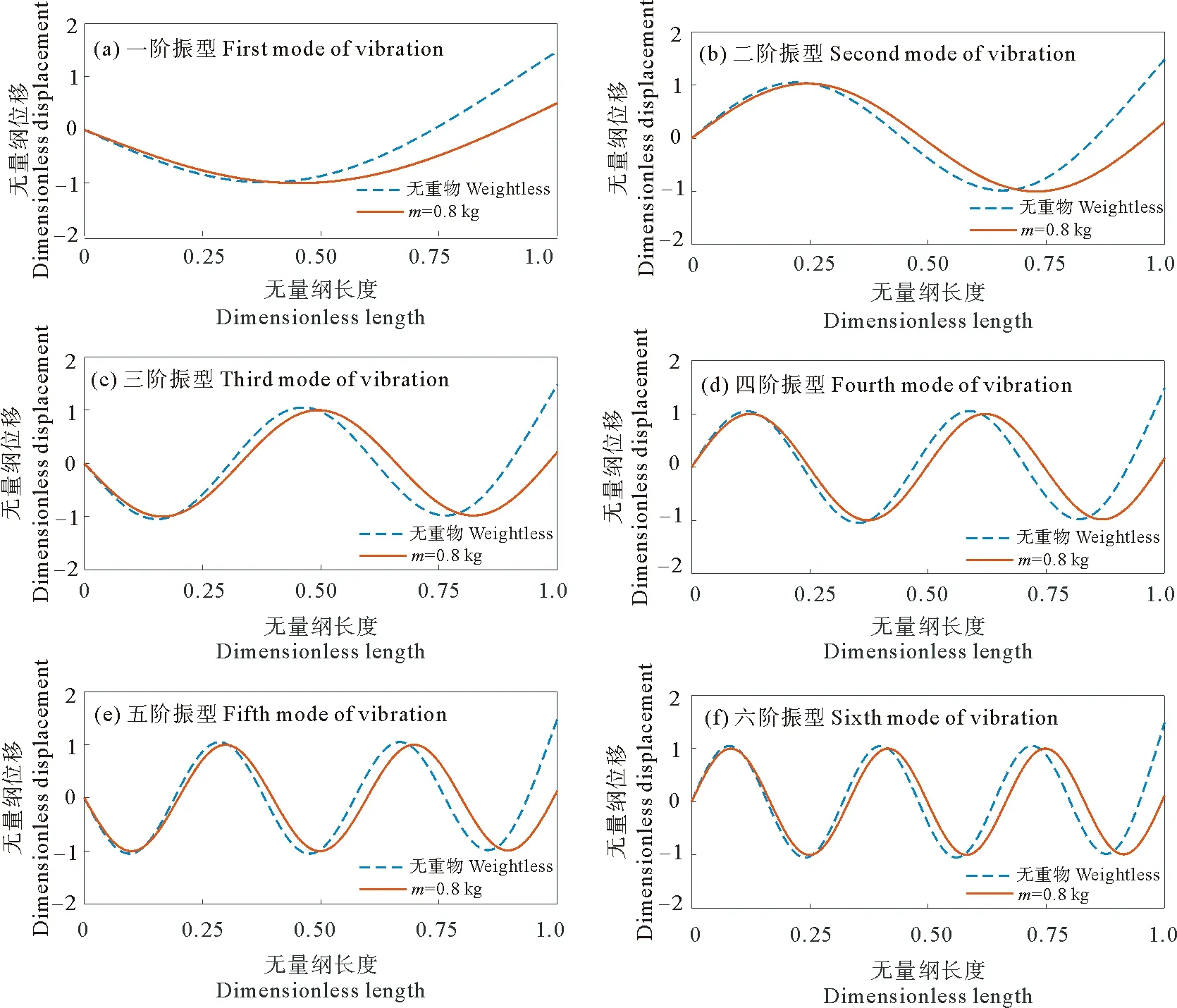
图4 悬挂0.8 kg重物立管模型与无重物悬挂立管模型的前六阶振型比较

3 结果与讨论

3.1 立管模型VIV特性

结合上述方法分析当流速为0.4 m/s、立管底部重物为0.8 kg时立管模型下放安装过程中的振动特性。图5为立管模型下放到100和300 s左右时1～6号应变测试点的应变特性。

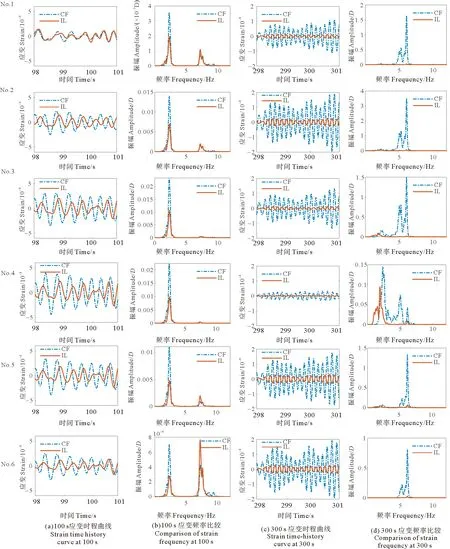
图5 下放到100 s和300 s左右时立管6个实验段的应变特性

在图5(a)列中每个应变测试点随时间都呈现出周期性的往复振动模式,且6个应变测试点在CF方向上的应变幅值略大于IL方向的应变幅值。立管的最大振动幅度出现在节点4附近,离节点4越远,振动幅度越小,符合立管的一阶振动特性。这是由于实验用以模拟LMRP的重物有不可忽略的长度,导致立管的中心点更接近节点4导致。在图5(b)列中立管的1～5号应变测试点在CF和IL方向上的主频均为2.3 Hz,略高于立管的一阶固有频率,因此在下放到100 s左右时立管以一阶振动模态为主。每个应变测试点的主频都相同,频率响应在CF和IL方向上的分布几乎相同,原因可能是实验采用的立管长细比不够大,在恒定的低速水流下,导致悬挂立管的自由端的两个方向频率相同,这种现象同Mao等[13, 17]的研究结果相吻合。立管的第六应变测试点在IL方向上出现了一个7.2 Hz的高频响应,这是因为当立管开始下放时,立管底端先浸入水面,底部悬挂物受到水流的冲击发生剧烈振动,因此在立管底部会出现以二阶频率为主的局部振动。

从图5(c)列中可以看出当立管下放到300 s左右时,立管的最大振动幅度出现在节点2和节点5附近,立管的中心节点4的振幅最小,每个应变测试点都呈现出应变随时间周期性的往复振动模式,且6个应变测试点上CF方向的应变幅值均明显大于IL方向的应变幅值,立管整体表现出以二阶模态为主导的振动,CF方向各实验断面的应变幅值远大于IL方向,IL方向的振动明显受到CF方向振动的干扰和控制。在图5(d)列中,在CF和IL方向上,立管的应变测试点(节点)1、2、3、4、5和6的主频均为6.1 Hz,与立管在水流中的二阶振动频率非常接近,因此立管在下放后期以二阶振动模态为主。除了节点4之外,每个应变测试点的主频都相同,且IL方向上的振幅要弱于CF方向,IL方向上的振动明显受到CF方向上振动的干扰和控制。立管的应变测试点4在CF方向上的主频为2.3 Hz,在IL方向上的主频为1.9 Hz,这是因为应变测试点4位于立管正中间,立管处于二阶振动时节点4的振动幅度最小,而一阶振动幅度最大,因此表现出局部一阶模态的振动特性。

图6分析了立管模型的位移时空云图。图6(a)—(b)分析了立管模型下放到100 s左右时在IL和CF方向上5个运动周期的弯曲应变分布。从图6中可以看出,立管在CF和IL方向上的应变都是非常规则并具有周期性的,表现出典型的行波特征,响应以第一种模式为主。另一方面,与CF方向上的响应相比,IL方向响应的规则性略差,且CF方向的应变要略大于IL方向应变。图6(c)—(d)展示了立管下放到300 s左右时的弯曲应变的分布,从图中可以看出,立管下放到300 s左右时应变响应变为典型的驻波特征,响应以第二种模式为主,且立管表现出来的规律与下放到100 s左右时一致,即在CF方向上响应的规律性要好于IL方向。

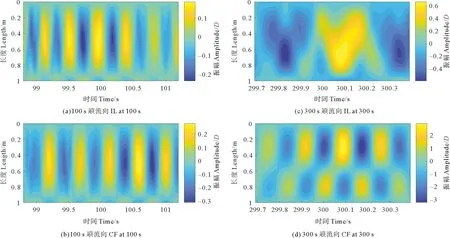
图6 下放到100 s和300 s左右时立管位移时空云图

3.2 立管下放时间对立管位形的影响

基于上述的位移重构方法分析立管沿长度方向上的振幅大小,每隔20 s绘制一次立管位形图(见图7)。从图中可以看出,当立管刚开始下放时,立管在两个方向上的振幅几乎相同,均表现出一阶模态。在下放过程的前160 s里,立管振幅变化很小,最大值约为0.02D,最小值约为-0.02D,立管底部位移约为0.003D,立管的最大振幅总是出现在立管的中点。随着立管模型的继续下放,振幅急剧增大。当立管下放到240 s时开始在CF方向上表现出明显的二阶模态,此时模型的振幅最大值为0.11D,最小值为-0.11D,最值点出现在x/L=0.3处,并且在IL方向上的振幅明显小于CF方向,立管底部位移约为0.01D。当下放进行到340 s时,振幅增加的速度逐渐变缓。下放到400 s时立管振幅约为0.31D,最小值为-0.30D,底部位移约为0.033D。

由图7分析可得立管模型在下放到180～320 s时振幅的增长速度最为剧烈,刚下放和即将完成下放时振幅变化较为平缓。立管底部自由端的振幅约为最大振幅的十分之一。立管模型在IL方向上的振幅曲线看起来不像CF方向那样对称,这与两个方面有关:1.VIV具有随机性;2.在立管下放过程中会受水流冲击从而在IL方向上产生一个较大的位移,这就导致立管在IL方向上的运动平面是一个倾斜平面,因此会出现振幅曲线不对称的现象。

3.3下放时间对立管振幅的影响

图8分析了当流速为0.4 m/s,立管底部重物为0.8 kg时,立管模型的振动幅值随下放时间的变化趋势。图8(a)为立管模型在安装下放过程中立管振动最大幅度,图8(b)为立管底部自由端的振动幅度。立管模型的最大振幅的下放时间在0～150 s时稳定在0.01D左右,且在两方向上表现得非常接近。下放到150 s后,CF方向上的振动幅度开始缓慢变大,在经历了50 s的过渡期后振幅增速加快,在400 s时达到0.3D。IL方向上的最大振幅则在250 s时出现增大趋势,并一直保持缓慢增加的速度直到下放结束,最大值约为0.09D。立管底部的振动幅度在前150 s一直保持稳定,下放到150 s时开始缓慢增大,直到下放结束,且在CF方向上的振幅一直大于IL方向。

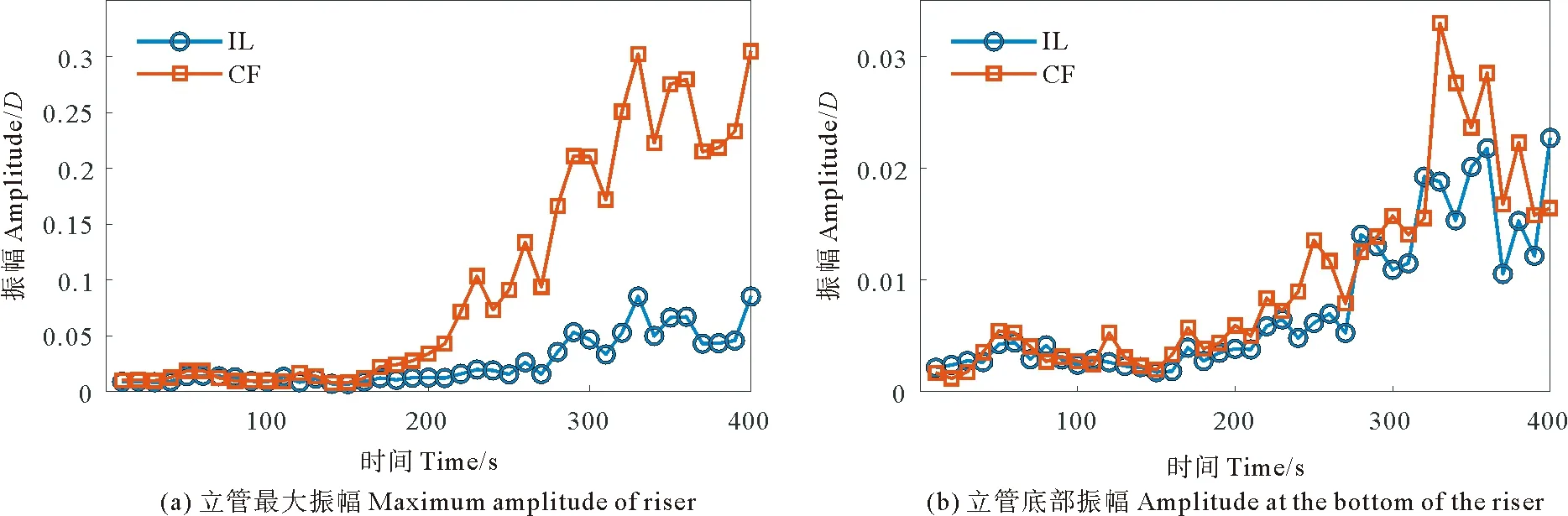
图8 立管安装下放过程中的振幅分析

3.4 LMRP质量对立管频率的影响

图9显示了在下放到100和300 s且立管底部LMRP质量分别为0.5、0.8、1.1和1.4 kg时第四应变测试点(z/L=0.575)的频率响应。可以看到刚开始下放时(100 s以前),立管模型以一个相对稳定的幅度低频振荡。频率响应由稳定的主频和一部分高频响应组成,且底部重物的质量越大,高频振动的参与越明显。不同LMRP质量对应的立管在CF方向上的主响应频率依次为2.49、2.29、2.44和2.59,在IL方向上的主响应频率依次为2.34、2.32、2.54和2.59。IL方向上的振动频率略大于CF方向,且立管底部悬挂的重物越大,振动频率越大,而振动幅度越小。当立管下放到300 s左右时,悬垂立管在CF方向上的主频显著增大,但在IL方向上的主频没有太大变化。不同工况下的立管在CF方向的振动幅度总是远大于IL方向,底部的重物质量越大,立管模型越偏向于高阶振动。不同质量的立管在CF方向上的主响应频率依次为5.42、5.28、5.28和5.16,立管的响应频率随着LMRP质量的增大而减小。

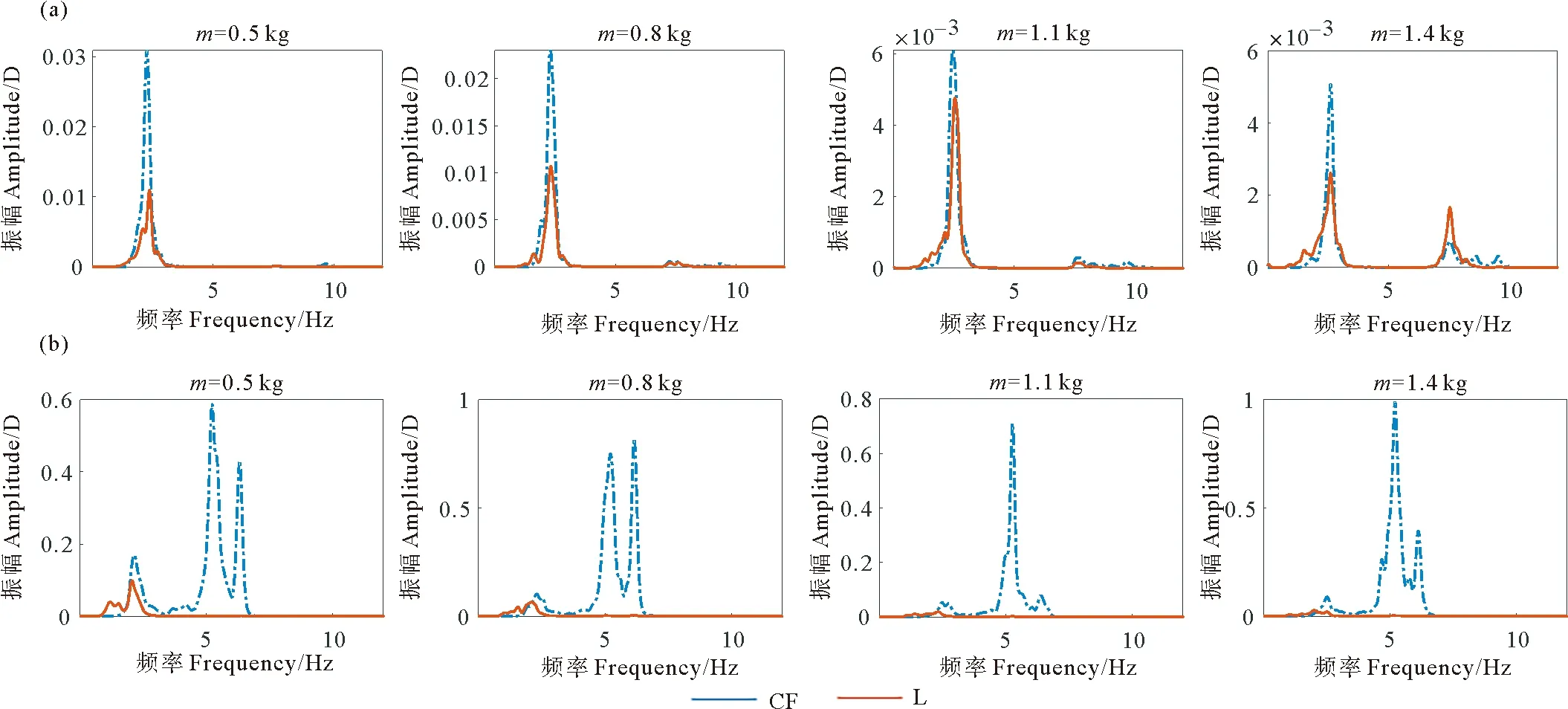
图9 100 s(a)和300 s(b)时各个工况下第四测试截面的振动响应

3.5 LMRP质量对立管振幅和位移的影响

图10给出了考虑底部悬挂不同质量重物时立管模型的振动幅度,显示了悬挂立管的振动模型形状。当立管下放到100 s时,立管主要表现出一阶振动模态,此时立管的振动幅度随着底部悬挂重物质量的减小而增大,且IL方向上的振幅要略小于CF方向。最大振幅均出现在立管中部x/L=0.5处。当m=0.5 kg时振动幅度最大,达到了0.02D。当m=0.8 kg时,由于底部质量的增加,立管的振动幅度大幅度减小,随着悬挂重物质量逐渐增大,底部重物的质量已经大大超过了立管本身的质量(0.8 kg),此时相当于立管模型由上端铰接下端自由转变成两端铰接,底部重物质量的增加(m=1.1 kg或m=1.4 kg)对立管振动幅度的影响已经微乎其微。

图10 100 s (a)和300 s(b)时四组工况下立管模型的振动响应比较

当立管下放到300 s时,立管在IL方向上仍表现为一阶振动,底部重物对立管的影响与立管刚开始下放时一样,振动幅度随着底部悬挂重物质量的减小而增大,当m=0.5 kg时振动幅度最大,达到了0.06D。在CF方向上主要表现出二阶振动模态,当m=0.5 kg时,最大振幅点在x/L=0.275处,随着底部质量的增大,立管最大振幅点会而出现下移现象。当m=0.8 kg时立管的振动幅度最大,达到了0.2D,此时LMBP质量近似于立管质量,最大振幅出现在x/L=0.3处。当底部LMBP质量大于立管自重时,立管的振动幅度大幅降低。当立管模型处在二阶振动模态时,底部质量的增大对自由端的振动幅度影响很小,4种工况下立管底部自由端的振动幅度均在0.02D左右。

图11(a)分析了在考虑了底部悬挂不同质量重物时立管模型的最大振幅。立管底部重物的质量大小对立管的最大振动幅度几乎没有影响,且CF方向上的振幅一直大于IL方向。立管模型的最大振幅的下放时间在0～150 s内表现出趋于稳定的极小值,且在两方向上表现得非常接近。下放到150 s后,CF方向上的振动幅度开始增大,在经历了50 s的过渡期后振幅突然增大,在400 s时达到0.3D。IL方向上的振幅最大值则在280 s左右时开始出现增大趋势,并一直保持缓慢的速度增加,直到下放结束,最大值约为0.08D。

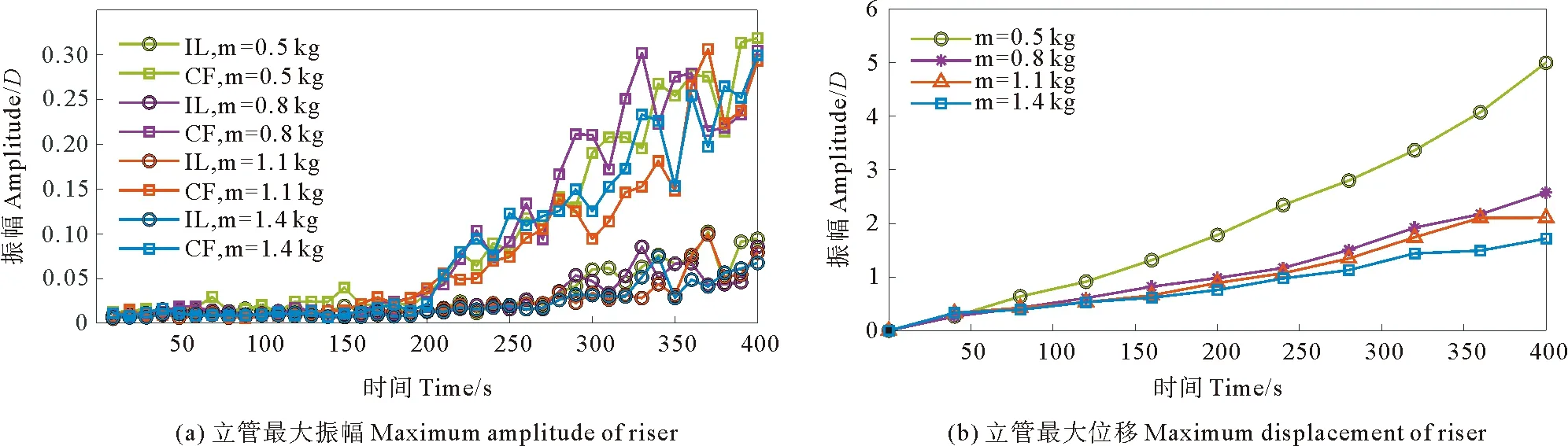
图11 安装下放过程中四组工况下立管模型的最大振动幅度和最大位移

图11(b)分析了悬挂不同质量重物的立管模型在IL方向上受水流拖曳力引起的位移,最大位移点始终位于立管模型底部。当重物m=0.5 kg时,立管底部的位移要远大于其他三种工况,当完成立管下放时,底部位移达到最大,约为5.0D。当底部悬挂的重物达到0.8 kg时,位移出现与立管振动相似的规律,由于重物质量已经接近管体本身质量(m=0.8 kg),底部重物质量的增加(m=1.1 kg或m=1.4 kg)对立管振动幅度的影响已经微乎其微,故当完成立管下放时,底部重物质量为0.8、1.1和1.4 kg对应的底部位移分别为2.5D、2.1D和1.8D。