基于极值拓展模型的广东汕尾增水推算*

刘桂林, 田雨航, 宋时春, 杨文锦, 尹精艺

(1． 中国海洋大学工程学院,山东 青岛 266100; 2. 青岛军民融合发展集团有限公司,山东 青岛 266500)

海洋工程结构经常处于各种极端海况中,一旦遭到破坏可能会造成重大的经济损失和人员伤亡,高估海洋工程设计标准会导致建造成本的大量增加,并造成不必要的浪费[1-3]。因此,准确推算海洋环境设计参数具有极其重要的现实意义。汕尾作为沿海城市,海洋资源丰富,大陆沿海岸线的长度在广东省排第二,拥有碣石湾和红海湾两个大海湾[4]。汕尾的海洋渔业、临海工业、海洋旅游业和海洋交通运输业蓬勃发展,近些年汕尾海洋经济总值占地区生产总值的35%以上,因而其海洋经济已经发展为地区经济增长的重要引擎。然而汕尾是中国受热带气旋侵袭严重的地区,频繁遭受海浪灾害的影响,属于高脆弱性城市[5]。风暴增水作为重要的海洋环境因素,海洋结构安全性和稳定性必然受其影响,因此准确推算汕尾地区的风暴增水设计参数可以为海上建筑物设计标准的制定提供依据,也是海洋工程结构设计至关重要的环节。

构建对观测数据拟合良好的概率模型是准确推算海洋环境设计参数的关键[6]。近些年拟合模型从传统的极值模型[7-8]发展到考虑风暴潮等灾害影响的复合极值模型[9-10],为降低模型的不确定性还引入最大熵分布[11-12]。尽管上述模型在不同方面提高了推算海洋环境设计参数的准确度,却很少讨论海洋环境设计参数作为随机变量,其极值样本数据具有“厚尾”特征的情况[13]。传统的极值分布只能很好地描述数据的尖峰(即概率密度最大的部分),其尾部却过快地趋于零[14-15],使得对极值数据的尾部拟合效果欠佳,导致在海洋工程设计标准研究和海洋灾害预警分析中对于高重现水平的计算结果存在一定误差,且重现期越长误差越大[16-18]。广义Pareto分布是常被用来估计极端事件的“厚尾”型分布,如Ross等[19-20]用广义Pareto分布拟合南海波高数据来估计极值有效波高,且得到只有在较高重现期(如千年一遇)下使用此模型,估算的重现值才相对稳定的结论,但广义Pareto分布不能拟合样本数据的尖峰,这限制了该模型对总体样本分布的分析[21-22]。若把能包络数据尖峰的经典极值分布与具有厚尾特征的Pareto分布进行组合,得到的模型将可以有效改善拟合极值观测数据的效果。

基于上述研究背景,针对传统极值分布对极值数据尾部拟合不足的问题,本文利用积分变限函数,借助传统极值分布和Pareto分布,构造出一系列既能拟合样本数据的尖峰部分又可以体现数据厚尾特征的极值拓展模型。将新模型应用于本研究中,具体研究流程为:处理汕尾增水实时观测数据;应用传统极值分布和新构建的极值拓展模型拟合极值增水数据并进行参数估计;检验各模型的拟合效果;验证极值拓展模型的尖峰厚尾特征;使用最佳拟合模型推算不同重现期下增水设计值,为确定汕尾地区的海洋和海岸工程设防标准以及分析工程结构安全性与可靠性提供参考。

1 理论模型

以积分变限函数为理论基础,借助组合函数的思想,将被积函数选取为对样本数据峰部拟合较好的传统极值分布,取对样本数据尾部特征拟合较好的Pareto分布的对数函数为积分上限函数,通过数学理论的逻辑推导,得到了极值拓展模型。

定理:设m(t)为随机变量t的概率密度函数,F(x)为Pareto分布。基于积分变限函数,构建m(t)为被积函数、F(x)的对数函数式[23]为积分上限的组合分布函数族H(x):

(1)

则,对应的概率密度函数h(x)为:

(2)

式中:随机变量t作为辅助变量,用来分析随机变量x的统计特性,从而使构造得到的组合模型同时具有2种分布的统计特性;f(x)为Pareto分布的概率密度函数。式(1)和(2)为组合模型的分布函数以及概率密度函数。

F(x)是对随机变量尾部拟合效果较好的Pareto分布,表达式为:

F(x)=1-σαx-α。

(3)

对应的概率密度函数f(x)表达式为:

f(x)=ασαx-α-1。

(4)

式中:α是形状参数,且α>0;σ是尺度参数,且x≥σ>0。

将式(3)和(4)分别代入式(1)和式(2),可以得到Pareto分布下极值拓展模型的通用分布函数H(x)和概率密度函数h(x)的显示表达式:

(5)

(6)

随着被积函数m(t)的不同选取,可以得到不同的极值拓展模型。

1.1 Gumbel-Pareto极值拓展模型(GPEED model)

取被积函数m(t)为Gumbel分布的概率密合度函数:

(7)

式中:t是辅助变量,t≥0;μ是位置参数,μ>0;b是形状参数,b>0。

将式(7)代入式(6)可以得到Gumbel分布下的极值拓展模型的概率密度函数:

(8)

式中:σ是Pareto分布的尺度参数;b是Gumbel分布的形状参数;α是Pareto分布的形状参数。将基于Gumbel分布和Pareto分布得到的极值拓展模型简称为GPEED(b,α,σ)。

1.2 Weibull-Pareto极值拓展模型(WPEED model)

取被积函数m(t)为Weibull分布的概率密合度函数:

(9)

式中:t≥0 ;c代表形状参数,c>0;γ表示尺度参数,γ>0。

将式(9)代入式(6),从而可以得到Weibull分布下的极值拓展模型的概率密度函数:

(10)

式中:σ是Pareto分布的尺度参数;c是Weibull分布的形状参数;α是Pareto分布的形状参数;γ是Weibull分布的尺度参数,α/γ=β。将基于Weibull分布和Pareto分布得到的极值拓展模型简称为WPEED(c,β,σ)。

1.3 Pearson-Ⅲ-Pareto极值拓展模型(PPEED model)

取被积函数m(t)为Pearson-Ⅲ分布,Pearson-Ⅲ的概率密合度函数为:

(11)

式中:t≥μ0,μ0是位置参数;ξ是形状参数;σ0是尺度参数;Γ(ξ)表示ξ的Gamma分布函数。

将式(11)代入式(6)可以得到Pearson-Ⅲ分布下的极值拓展模型的概率密度函数:

(12)

式中:σ是Pareto分布的尺度参数;ξ是Pearson-Ⅲ分布的形状参数;α是Pareto分布的形状参数;σ0是Pearson-Ⅲ分布的尺度参数;Γ(ξ)是具有满足递推关系和阶乘关系的Gamma函数;ασ0=β。将基于Pearson-Ⅲ分布和Pareto分布得到的极值拓展模型简称为PPEED(ξ,β,σ)。

2 工程应用

为保证汕尾地区海洋工程建筑的安全,本文基于汕尾观测站(115.366 7°E,22.766 7°N)1990—2012年间的实测增水数据,如图1所示,其中蓝色柱状图代表实测增水数据,红色柱状图代表通过极值法取样得到的每年增水的极值数据,为保证样本间的独立性,每年只选取一个最大的增水实测数据进行分析,然后通过极值法得到年极值增水数据的峰度为3.819,即汕尾地区年极值增水数据具有“厚尾’特征[13],所以要选取厚尾型分布才能充分拟合数据的尾部,这是合理推算高重现期下增水设计值的关键。因此,本研究分别利用传统极值模型和新构建的极值拓展模对极值增水数据进行拟合,通过对比分析找到拟合汕尾增水数据的最佳模型,为制定汕尾地区的海洋工程设防标准提供参考。

图1 实测数据与年极值样本数据

2.1 模型的选择与参数估计

由于广义极值分布(GEV)参数取特定值即可得到广泛应用的Gumbel分布和Weibull分布,所以本文将GEV作为拟合极值增水数据的第一种模型。由于最大熵分布受人为假设影响少,模型不确定度小,所以近些年来被广泛应用,中国水文领域最为常用的Pearson-Ⅲ分布正是最大熵分布的一种特殊形式,因此本文将最大熵分布作为拟合极值增水数据的第二种模型。将本文1.1—1.3提出的一系列极值拓展(GPEED、WPEED和PPEED)模型作为拟合极值增水数据的第三种模型,通过上述模型对汕尾增水数据展开研究,极值拓展模型具体表达式已经在本文1.1—1.3中给出。

广义极值分布(GEV)的概率密度函数可以表示为:

(13)

式中:1+ξ(x-μ)/γ>0;μ是位置参数;γ是尺度参数;ξ是形状参数。

最大熵分布(ME)的概率密度函数可以表示为:

h(x)=mxnexp(-γxξ)。

(14)

式中:m=exp(λ-1),其中λ为Lagrange乘子;γ是尺度参数;ξ是形状参数。

参数估计采用极大似然法(MLE),基于R语言使用Simulated-Annealing方法(SANN)对似然函数进行数值求解,得到模型参数的似然估计值,各模型参数估计的结果如表1所示。

表1 各模型参数估计值

2.2 模型的拟合检验与分析

利用MATLAB软件绘制概率图(PP图)、分位数图(QQ图)、重现水平图和概率密度图,检验各模型拟合数据的情况。若指定的模型能较好地拟合实测数据,则PP图的实测数据点和QQ图中的实测数据点均应在对角线直线附近,重现水平图中的数据点均应在模型曲线附近,概率密度图的模型曲线应与频率分布直方图的形状一致。广义极值分布、最大熵分布和3种极值拓展模型拟合汕尾极值增水数据的检验结果分别如图2—6所示。

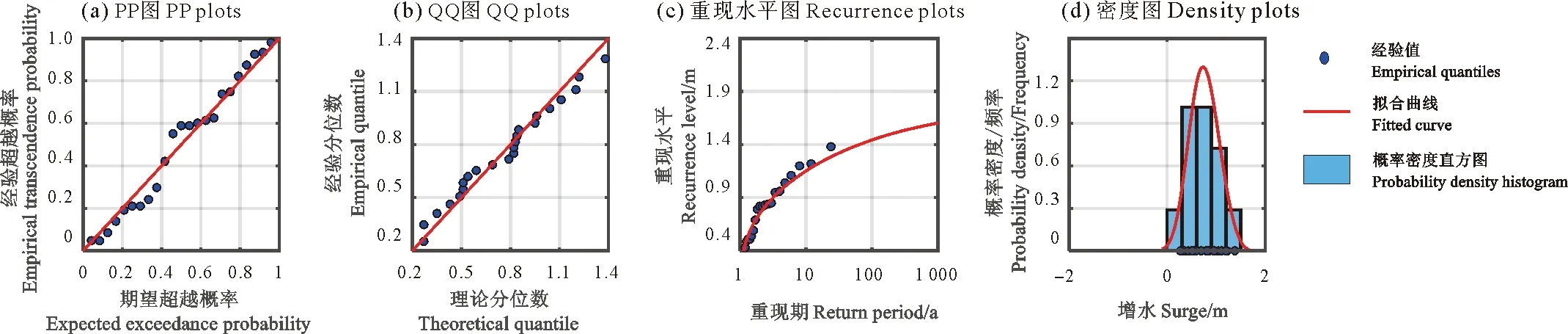
图2 广义极值(GEV)分布拟合增水检验

图3 最大熵(ME)分布拟合增水检验

图4 Gumbel-Pareto极值拓展模型拟合增水检验

图5 Weibull-Pareto极值拓展模型拟合增水检验

图6 Pearson-Ⅲ-Pareto极值拓展模型拟合增水检验

由图2—6可知,广义极值分布、最大熵分布和3种极值拓展模型都能较好地拟合汕尾年极值增水数据。

为进一步验证上述模型拟合极值增水数据的合理性,对以上5种模型的拟合分别进行K-S检验[24],置信水平取0.05,检验的临界值为0.274 9,检验结果如表2所示。表2中:K-S检验一列括号内的值为统计量, 所有模型的统计量均小于临界值0.274 9,说明均通过了K-S检验,可以用于拟合年极值增水;括号上面的值为检验的p值,p值越大说明模型的拟合效果越好,由此可得拟合增水效果最好的分布为GPEED。赤池信息准则(Akaike information criterion, AIC)值与贝叶斯信息准则(Bayesian information criterion, BIC)值也均可用于检验模型对于数据的拟合情况,其值越小说明拟合效果越好[25],根据表2的计算结果也可以得到拟合效果最好的分布是GPEED,与K-S检验结论一致。

表2 不同模型对于增水的拟合优度检验

2.3 尖峰厚尾特征分析

通过概率密度函数可以进一步分析模型对于数据的拟合情况,为方便对比分析,将广义极值分布、最大熵分布以及3种极值拓展模型的概率密度函数放在一起。为进一步对比本文所研究的各种模型对极值增水数据的拟合情况,图7给出了各种模型的概率密度函数图以及直方图。

图7 概率密度函数图

由图7可知,GPEED、WPEED和PPEED模型的概率密度函数的峰值同直方图峰值的位置更接近,即相较于广义极值分布峰值位置和最大熵分布峰值位置更偏左,且这3种极值拓展模型的概率密度函数的尾部相较于广义极值分布和最大熵分布也更厚。这是因为基于组合模型原理,借助积分变限函数推导出的极值拓展模型融合了经典极值分布的“尖峰”特征和Pareto分布的“厚尾”特征,所以能够同时更好地拟合数据的尖峰和厚尾。并且从图7中还可以得到结论,GPEED模型对于增水直方图的拟合效果更好。这一结论同2.2节的分析保持一致。为更清晰地对比不同分布函数的拟合效果,表3给出了不同增水条件下各模型密度函数的值,可以看出GPEED、WPEED和PPEED模型的尾部函数值均明显大于另外2种模型,且在这3种极值拓展模型中,GPEED尾部值最大。

表3 不同模型概率密度函数拟合增水的尾部值

2.4不同重现期下增水推算

由2.2小节可知,Gumbel-Pareto极值拓展模型拟合汕尾地区年极值增水数据效果最佳,利用该模型对汕尾极端增水进行概率分析,推求不同重现期下增水的设计值,为分析广东汕尾地区海洋与海岸工程结构安全、制定更为合理的海洋工程设计标准提供参考,分析结果如表4所示。

表4 各重现期下增水设计值

3 结语

本文利用新构建的一系列极值拓展模型、广义极值分布和最大熵分布拟合1990—2012年间汕尾观测站的实测极值增水数据,并从图形检验、拟合优度检验和尖峰厚尾检验三个方面对比分析传统模型与极值拓展模型对极值数据的拟合情况。发现相较于传统模型而言,极值拓展模型能同时拟合极值观测数据的峰部与尾部,其概率密度曲线具有单尖峰、厚尾的特性,其中对汕尾极值增水数据拟合最好的模型是Gumbel-Pareto极值拓展模型,用该模型推算汕尾百年一遇和千年一遇的增水分别为2.973和3.710 m。极值拓展模型具有能够同时拟合数据“尖峰”和“厚尾”的特点,但本研究只应用该模型对增水一种海洋环境设计参数的设计值进行推算。实际上,风速、波高和流速等参数对海洋工程的建设和安全也有较大的影响。应用极值拓展模型拟合风速、波高和流速等参数的极值观测数据,并且综合考虑增水、风速、波高和流速等多个环境参数对海洋工程结构物的联合作用,将是进一步的研究方向。