一类带凹凸项的椭圆型偏微分方程解的存在性
2023-09-25郑文静陈尚杰
郑文静,陈尚杰,李 麟
(重庆工商大学 a.数学与统计学院,b.经济社会应用统计重庆市重点实验室,重庆 400067)
考虑如下发展方程

(1)
当方程(1)寻找自相似解w(t,x)∶=t-1/(p-2)u(t-1/2x)时,方程(1)等价于一类带权重K(x)的热方程

(2)
具体见文献[1]。热方程作为抛物型偏微分方程,不仅可以用来描述热传导过程,也可以用来描述多种反应的扩散过程,诸如液体流动、传染病扩散、生物种群的迁移、生物分子的运动以及飞行器的冷却与保护等。
在最近的文献[2]中,Li和Tang研究了在非线性项f(x,u)分别满足超线性和渐近线性的情况下方程(2)基态解的存在性。除此之外,更多的学者研究了方程(2)中非线性项f(x,u)=a(x)|x|β|u|q-2u+b(x)u2*-2u的情况,即如下方程:

(3)

值得一提的是,文献[8]研究了如下带有凹凸项的椭圆型偏微分方程

其中1 与上述方程略有不同,在文献[11]中,Qian和Chao考虑了如下带非局部项的椭圆型偏微分方程 (4) 非平凡解的存在性问题,其中a,b,λ>0,β=(α-2)(6-q)/4,K(x)=exp{|x|2/4},α≥2。在对参数λ作不同的假设条件下,作者利用山路定理和Nehari流形的方法分别证明了方程(4)非平凡解和基态解的存在性。同样方法应用到其他方程的研究可见文献[12]。 受文献[8-11]启发,本文将研究如下一类带有一般凹凸非线性项的椭圆型方程 (5) (f3):存在L0>0,θ>4和C1>0,使得 在上述条件下,本文得到以下结果。 定理1假设(g1)(g2)和(f1)—(f4)成立,则存在μ0>0当|μ|≤μ0时,问题有无穷多个解。 注记1受权重的影响,本文得到的解呈指数衰减,证明可参见文献[3],且关于方程,目前还未有类似结论。 对每一个q∈[2,6],定义空间 (6) 显然,I(u)是连续可导泛函,且其导数形式为 (7) 如果u∈X,∀v∈X满足〈I′(u),v〉=0,则称u∈X是问题的弱解。 1)对每一个有限维子空间V⊂X,存在R=R(V)使得当‖u‖≥R时有I(u)≤0; 2) 存在常数ρ,α>0,使得I(u)|{u∈Z:‖u‖=ρ}≥α; 3)泛函I满足(PS)c条件, 则泛函I有一列无界的临界值序列{un}。 本文主要是运用变分法[14]求解的方法,通过山路定理得到方程无穷多解的存在性,故在证明定理1之前,本文需要引入一些预备结论。 证明类似于文献[15]。 引理2 假设条件(f2)和(g1)成立,则对X的每一个有限维子空间V,存在R=R(V)使得当‖u‖≥R时有I(u)≤0。 证明利用反证法,设对于任意的n∈,存在序列{un}⊂V使得‖un‖→∞时,有I(un)>0。首先取vn=,显然‖vn‖=1,即序列{vn}在X中是有界的,又因为V是有限维的,所以存在v∈V和序列{vn}的一个子列(仍记为{vn})使得vn→v,‖v‖=1,且对于任意x∈3有vn(x)几乎处处收敛于v(x)。定义一个集合B={x∈3:v(x)≠0},显然meas(B)>0,并且对于a.e.x∈B,n→∞时,有|un(x)|→+∞成立。则由条件(f2)和Fatou引理可得 (8) 根据(g1)、定理2和Hölder不等式得 又因为1 (9) 结合(8)(9)和I(un)>0可得 显然不等式两边矛盾,I(un)>0的假设不成立,故存在R=R(V)使得当‖u‖≥R时,I(u)≤0。证明结束。 引理3假设(g1)和(f1)成立,存在常数ρ,α>0,对任意|μ|≤|μ0|,使得I(u)|{u∈Z:‖u‖=ρ}≥α。 证明由条件(f1)可得 结合(6)(9)和引理1—2,对任何u∈Z满足‖u‖≤1有 引理4假设(g1)(f1)(f2)和(f3)成立,则泛函I满足(PS)c条件。 证明设{un}是泛函I的一个(PS)c序列,即 I(un)→c,I′(un)→0。 (10) 定义集合B={x∈R3:v(x)≠0},则meas(B)≥0。接下来分别考虑如下两种情况: 情形(1):meas(B)>0。这种情况的证明与引理2类似,故可由(8)(9)得 显然不等式两边矛盾,所以在meas(B)>0时,序列{un}在空间X中是有界的。 |f(x,t)t|≤c0(|t|2+|t|p)≤2c0|t|2。 (11) |f(x,t)t|≤c0(|t|2+|t|p)≤M≤M|t|2。 (12) |f(x,t)t|≤(2c0+M)|t|2, 从而存在常数C2>0,有 结合(f3)得 由(g1)和Hölder不等式及定理2可得 因为1 从而有 现需再证序列{un}在X中有一个子列强收敛于u,即在空间X中有‖un-u‖→0。因为序列{un}是有界的,所以存在一个子列{un}(仍记为{un})和u∈X使得 注意到 〈I′(un)-I′(u),un-u〉=a(un,un-u)+b‖un‖2(un,un-u)-a(u,un-u)-b‖u‖2(u,un-u)+ =a‖un-u‖2+b‖un‖2‖un-u‖2+b(‖un‖2-‖u‖2)(u,un-u)+ 整理得 因此要证‖un-u‖→0,只需证明下列式子成立 (13) (14) b(‖u‖2-‖un‖2)(u,un-u)→0。 (15) 〈I′(un)-I′(u),un-u〉→0。 (16) 由(f1)和Hölder不等式有 由(g1)和Hölder不等式有 定理1的证明根据条件(g2)和(f4)知,函数F和G是偶函数,则泛函I是偶的,由引理2和引理3知,泛函I满足定理3的条件1)和条件2),又从引理4中知,泛函I满足(PS)c条件,从而满足定理3,因此可由定理3直接得到方程(5)有无穷多个解。证毕。







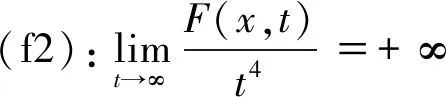


1 预备知识





2 主要结果证明